引力电、引力磁与引力波

何孝凯,曹周键

(1. 湖南第一师范学院 数学与统计学院,湖南 长沙 410205;2. 北京师范大学 天文系,北京 100875)

电磁现象和引力现象的相似性是一个值得人们深入思考的问题.牛顿的万有引力平方反比定律和库仑的静电力平方反比定律最先引起人们注意到这个相似性的对比.在电流间的安培力被发现以后,人们花了很多努力去寻找引力的“安培力”对应.在牛顿时空观的理论框架下,这些努力失败了.

引力“安培力”的问题在一定程度上引导马赫原理被提出,进而助力了广义相对论的诞生.在广义相对论框架下,人们发现磁型引力场对应引力“安培力”.后来人们发现在弱场、低速近似下,爱因斯坦方程表现为类似麦克斯韦方程的形式.该方程与麦克斯韦方程只差到一个符号.这一符号差异导致引力迈斯纳效应[1]和引力发电机不存在[2].

本文不着力于探讨电磁现象和引力现象的物理实质相似性,而是重点关注它们之间形式的相似性问题.作为广义相对论理论核心的爱因斯坦方程预言了引力波的存在.在平直时空背景下传播的引力波可以被描述为平直时空的微扰.在弱场、低速条件下,爱因斯坦方程和麦克斯韦方程非常类似,而麦克斯韦方程可以描述电磁波,那么弱场、低速近似下爱因斯坦方程的引力电和引力磁是否可以在形式上被用来描述引力波呢?这就是本文将要重点讨论的问题.在本文中我们采用几何单位制c=G=1.

1 引力电、引力磁和类麦克斯韦方程

考虑低速、低密度的物质场,用数学的语言描述就是说存在一个坐标系可以将时空度规场表述为

gμν=ημν+hμν

(1)

|hμν|<<1

(2)

同时物质场的能动张量可以表达为

(3)

|vi|<<1,ρ～O(ε)

(4)

这里ημν是闵氏度规,ρ是物质场能量密度,为小量,记为O(ε),v=(v1,v2,v3)为物质的速度场.能动张量的空-空分量是速度平方的量级,此处已被当作速度的高阶小量忽略掉.

度规式(1)对应的克氏符为

(5)

对于里奇张量,保留到一阶,有

根据式(5),有

(6)

利用反迹张量记号：

可以将调和规范条件表述为

(7)

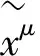
在上式的最后一步中用到了Tμν和ξμ都是小量.

上面的论述表明,可选取调和规范并满足式(1)—(4).为记号简便,接下来采用这样的规范并丢掉记号中的波浪符号.此时,爱因斯坦方程变为

(8)

由此可以求得推迟解：

其中B(r,t′)表示r为球心t′为半径的坐标球壳.现引入类电磁学记号：

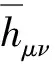
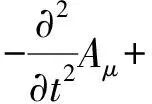
(9)

将引力电磁四势Aμ和引力电流Jμ代入调和规范条件,得到类洛伦兹规范条件：

(10)

我们可以进一步引入类似电磁学的标势和矢势以及引力电场、引力磁场记号：

φ≡A0,A≡(A1,A2,A3)

E≡

(11)

B≡×A

(12)

对式(11)取散度,得

(13)

上式的最后一步用到了式(9).

对式(11)取旋度,得

其中j≡(J1,J2,J3).

至此,我们就得到了完整的类麦克斯韦引力电磁方程组[3]：

(14)

(15)

(16)

(17)

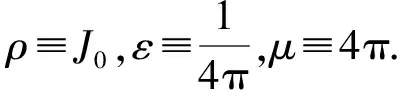
除了式(14)右端的负号,上述方程组形式上与麦克斯韦方程组完全一样.

2 远场区的引力电和引力磁

在现实的物理系统中,物质场的分布都在有限区域.在这个区域以外,物质场变成零,对应的类麦克斯韦方程式(14)—(17)变成无源方程组. 形式上该方程组和无源麦克斯韦方程组完全一样,而远场区变成引力波的波动区. 这自然让我们联想,这个无源的类麦克斯韦方程组是不是正好描述引力波.

不失一般性,考虑沿x方向传播的单色平面类电磁波解：

E=E0cos(kx-ωt),B=B0cos(kx-ωt)

等价地,有

(18)

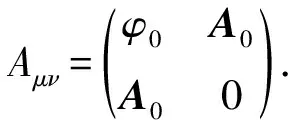
根据类麦克斯韦方程的性质,可知类电磁波解的传播速度为光速,所以k=ω.将式(18)代入调和规范条件式(7)得到

ωφ0+kA0x=0

(19)

φ0=-A0x

(20)

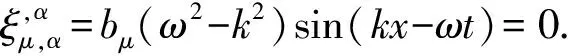
根据式(6),通过直接计算可以发现坐标变换后仍然满足调和规范,同时Aμν变为

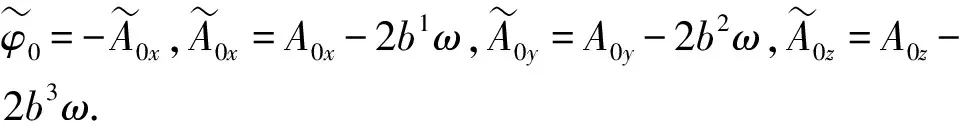
实际上,上述的规范变换或者说坐标变换对应通常教科书中描述引力波常用的横向无迹规范[4].换句话说,远场区的引力电和引力磁对应的横向无迹规范引力波等于0.

3 讨论

上节分析表明远场区的引力电和引力磁对应的平直时空微扰张量可以通过规范变换变成0.由此,我们自然想到一个问题,是否引力电和引力磁完全是规范效应,没有物理实质.答案是否定的.引力电和引力磁具有很好的物理意义,在弱引力场和后牛顿近似中有广泛应用.问题的关键在于有源和无源的区别以及稳态和波动的区别.

在无源区,我们可以使用横向无迹规范.因为横向无迹规范很重要的一个条件是真空爱因斯坦方程.非真空情形下横向无迹规范不存在,上一节讲到的规范变换也不成立.所以,在有源区引力电和引力磁可以有效地、方便地刻画引力场.重要的是,本文的分析表明,这样的引力电和引力磁传不远,它们不能脱离引力源存在,自然也就不能描述脱离引力源传播的引力波.

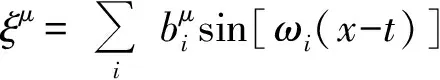
双星系统是人们最为熟悉的引力波源[5-7].对比本文的分析,我们会问,难道间距很大的双星系统不能做如式(3)的弱场、低速近似.对于双星系统,能量动量张量可写为[8]

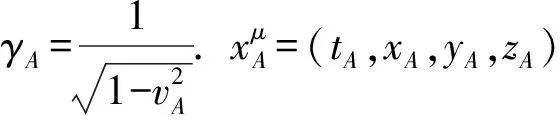
引力电和引力磁是后牛顿分析中经常使用的概念,常伴随后牛顿规范使用. 后牛顿规范中强调的低速就是相对物质而言的,没有物质就谈不上低速.后牛顿规范中的低速既是对物质性质的要求也是对规范选择的要求.本文的分析让我们体会到,后牛顿规范是在源区附近使用的概念.这是为什么在地球附近的卫星项目检验广义相对论效应的时候可以使用引力电和引力磁[9-12],原因就是所涉及的源场区附近的引力场行为.

另外值得指出的是,文献中还有另外一种形式的引力电和引力磁的概念.这种引力电和引力磁是通过曲率张量的相关分量来定义的[13].此种形式的引力电和引力磁完全对应引力波的概念.但这种形式的引力电和引力磁对应的动力学方程除了是对偶形式物理量和相关性质与电磁场有些类似之外,方程形式与麦克斯韦方程很不一样.