基于互质阵列的近场源位置估计方法

王绪虎, 田雨, 张群飞, 李恩玉, 金序, 侯玉君

(1.青岛理工大学 信息与控制工程学院, 山东 青岛 266520; 2.西北工业大学 航海学院, 陕西 西安 710072)

0 引言

随着第5代移动通信(5G)技术的发展,车联网(IOV)[1-2]技术成为未来发展趋势之一,而车辆定位[3-5]技术是IOV的重要分支,需要十分精确的位置和方向信息用于路径规划和安全操作,并且获取信息不会受天气因素和周围环境的影响。车辆位置可以借助北斗卫星导航系统(BDS)获得,但该方法时延和估计精度误差很大,尤其在隧道或云层较厚等环境中,极大影响该方法的使用,因此无线网络协作定位方法[6-7]成为车辆定位的研究方法之一,常用的方法是波达方向(DOA)估计,即通过无线接入点(WAP)与车辆传感器阵列共同配合,实现估计方位和距离功能,从而确认车辆位置。

阵列孔径是影响估计精度因素之一,与均匀线列阵相比,互质阵列具有高自由度(DOF)的优势,且能克服均匀线列阵间距受半波长限制的缺陷,因此互质阵列研究逐渐受到学者的重视。与互质阵列传统方法[8-12]相比,基于压缩感知和稀疏重构的DOA估计方法,在低信噪比(SNR)或少快拍数等情况下能表现出更准确的估计精度,因此文献[13-17]提出了互质阵列的各种处理方法,然而上述方法主要是针对远场信号提出的,无法直接套用在近场信号模型。针对近场模型,许多学者将传统的多重信号分类(MUSIC)方法进行了改进,提出了新的基于子空间的近场源(SLONS)定位方法[18]、降维MUSIC(RDMUSIC)方法[19]和改进近场MUSIC(INF-MUSIC)方法[20]等,上述方法不需要二维峰值搜索便可实现位置估计,并且可以实现估计角度与距离的一一匹配,大大降低了计算复杂度。然而,上述方法进行了降维处理,依然需要多次一维搜索,会影响该方法的估计精度。文献[21]在L1范数奇异值分解(L1-SVD)方法基础上,提出了一种重新加权平滑的L0范数稀疏近场参数估计方法,该方法大大降低了计算复杂度。文献[22]提出了一种无搜索近场源定位方法,通过参数分离和多项式根运算,获得了信号方位估计和距离估计值,该方法避免了谱搜索和参数配对,提高了估计性能。上述方法都基于均匀线列阵,所能估计的信源数受到阵元数目的限制,估计多个目标位置信息会增大系统硬件成本开销。互质阵列能有效地解决这一问题[23],因此本文提出了一种基于互质阵列的近场源定位估计方法。所提方法通过迭代方法来逐步修正角度偏移向量,从而得到角度参数估计值;将已估计出角度值代入模型,通过迭代方法来逐步修正距离偏移向量,得到距离参数估计值。所提方法的处理过程能自动匹配估计角度与估计距离,同时在数据预处理过程中,使用对称阵列的协方差,消除了噪声的影响,提高了入射角度和距离的估计精度。

1 近场源信号模型

两个不同间距的均匀线列阵嵌套构成一个稀疏阵列,互质阵列近场信号源模型如图1所示。阵元的位置索引可表示为Ω=-ΩC∪ΩC,其中

ΩC={Mn|0≤n≤(N-1)/2}∪ {Nm|0≤m≤(M-1)/2}

(1)

式中:M和N为互质的整数。阵列1是N元均匀线列阵,间距为Md,阵列2是M元均匀线列阵,间距为Nd,d表示单位间距,一般将其设为d=λ/4,λ表示波长。

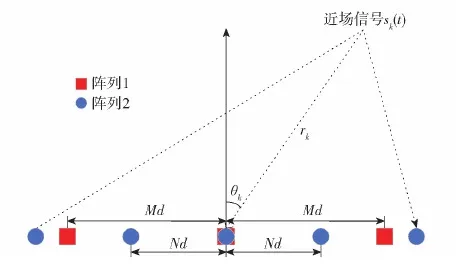
图1 近场信号源模型结构图Fig.1 Model configuration of near-field source

假设K个近场信号源入射到该互质阵列上,入射角度为θ=[θ1,…,θk,…,θK],θk表示第k个信源与参考阵元的角度,入射距离为r=[r1,…,rk,…,rK],rk表示第k个信源距参考阵元的距离,sk(t)表示第k个信号源,其中k=1,2,…,K,则第i个阵元相对于参考阵元来说,相对时延为

(2)

式中:Ωi表示第i个阵列的索引1≤i≤M+N-1;c表示信号的传播速度。借助泰勒展开式,忽略 3阶及以上阶数的项数,则得到相对延迟相位为

(3)

阵列接收数据模型为

Y(t)=A(θ,r)s(t)+n(t)

(4)

2 离网格稀疏表示估计方法

2.1 角度参数估计

第Ωi1个阵元与第Ωi2个阵元之间的空间相关性可以写为

(5)

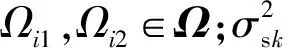
(6)

将式(6)写成向量的表达形式,得到

(7)

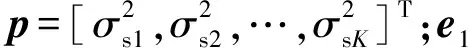
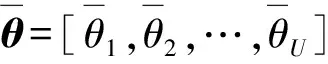
(8)

式中:pθ表示网格点对应的功率,是实际功率p的零扩展。如果信号源的入射方向不在预设的网格上,则借助泰勒展开式得

(9)

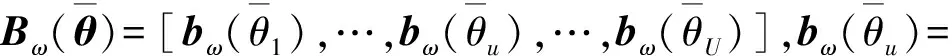
(10)

(11)

然而上述问题会存在NP-Hard问题,文献中已经提出了各种方法来解决优化公式(11),其中有代表性的是LASSO方法,该方法将式(11)中的L0范数用L1范数代替。文献[16]利用对数和的方法进行推导,未知的功率矢量pθ和网格误差δθ可以用以下方法求解:

(12)

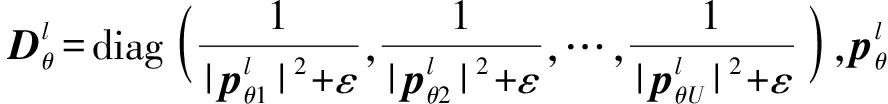
(13)

(14)

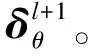
(15)

式中:μ1表示角度网格的梯度下降系数。令式(14)中的参数表示为

(16)

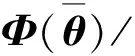
(17)

式中:eu表示U×1维的单位列向量,第u个位置为1,其他位置全为0。

(18)

则∂f1(δθ)/∂δθ可得

(19)

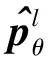
(20)

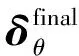
2.2 距离参数估计

在得到估计角度后,新的接收数据模型变为

Y(t)=Aφ(,r)s(t)+n(t)

(21)

式中:Aφ(,r)是关于距离r的流形矩阵,表示K个估计值,Aφ(,r)=[aφ(1,r),…,Aφ(K,r)],信源距离r的分布空间为[0.62(D3/λ)1/2,2D2/λ],D为阵列孔径大小。参照DOA求解过程,本文将信源距离r的空间均匀划分V份,得到网格点集合为Γ=[r1,r2,…,rV],进而得到离格场景下的稀疏模型为

Y(t)=Aφ(,Г)x(t)+n(t)

(22)

式中:x(t)表示原始信号s(t)的0扩展,在接近信号距离位置有值,其他位置全为0;Aφ(,Γ)=[aφ(1,Γ),…,aφ(K,Γ)]表示离散距离的完备基流型矩阵。假设信号与参考阵元之间的距离不在预设网格上,那么则借助一阶泰勒展开式得到

Υ(,Γ)≈Aφ(,Γ)+Bφ(,Γ)diag(δr)

(23)

式中:Bφ(,Γ)=[bφ(1,Γ),bφ(2,Γ),…,bφ(K,Γ)],bφ(,Γ)=∂aφ(,Γ)/∂Γ;δr表示距离误差,δr=[δr1,δr2,…,δrV]。在存在距离网格条件下,阵列接收数据表达式为

Y(t)=Υφ(,Γ)x(t)+n(t)

(24)

因此,得到的实际接收数据与离网格模型接收的数据误差达到最小,定义目标函数为

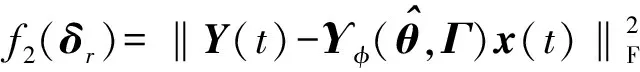
(25)

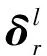
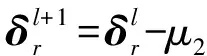
(26)

式中:μ2表示距离网格的梯度下降系数。令Cv=∂Υφ(,Γ)/∂δrv=Bφ(,Γ)diag(ev),ev表示V×1维的单位向量,在第v个位置为1,其余位置为0,1≤v≤V。则对距离误差矢量某一个元素求导∂f2(δr)/∂δr,得

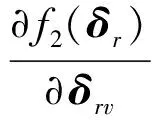
(27)

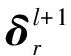
(28)

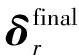
2.3 本文方法步骤

离网格互质阵列近场信号位置估计的实现过程为:

1)得到近场模型的接收数据,采用式(7)的思想构造新的协方差数据rθ;

2)将空间区域[-π/2 rad,π/2 rad]均匀划分成U份,得到式(10)离散网格模型;

3)固定角度网格间距δθ,利用式(13)求功率θ;

6)将距离区域[0.62(D3/λ)1/2,2D2/λ]均匀划分成V份,得到式(24)离散网格模型;

7)得到定义的最优化问题,将式(25)中距离网格误差矢量进行求导,利用式(26)梯度下降原理得到网格误差δr;

8)当满足距离误差精度的条件,利用式(28)确定入射角度所对应的距离,否则进入步骤7,直到满足条件或者达到最大迭代次数停止,最后输出入射角度与距离所对应关系的图像。

3 仿真实验仿真及性能分析

为了验证所提方法在DOA估计方面的卓越性能,并与其他现有的方法进行比较,包括SS-MUSIC方法[13]、JLASSO方法[14]、ESPRIT方法等。在仿真实验中,SS-MUSIC和ESPRIT方法需要提前知道信号源个数,而其他方法则不需要假设信源数。在空域区间-90°～90°划分网格,步长3°,选择菲涅尔模型距离区间,以步长3 m划分网格。模拟条件下SNR为10 dB,快拍数取500。考虑互质阵列中子阵列传感器数量M=5、N=3,则互质阵列阵元位置索引为Ω=[-6,-5,-3,0,3,5,6]。

3.1 仿真实验

3.1.1 功率谱图分析

为了验证所提出的方法在DOA估计的可行性,与SS-MUSIC方法和JLASSO方法进行比较。取K=3个窄带不相关的近场信号源,角度与距离分别为[-22.87°,25.42 m]、[25.19°,34.66 m]和[43.21°,59.18 m],得到归一化功率谱图如图2所示。

图2 各类方法的归一化功率谱图Fig.2 Normalized power spectra of various methods

图2的仿真结果表明上述3种方法都能估计出信号的入射角度θ。但是,从归一化功率谱图上可以看出,JLASSO方法会在实际入射角度位置产生伪峰,极大地影响了该方法的估计性能,SS-MUSIC方法与本文方法都能估计出信号角度,但是SS-MUSIC方法的估计精度取决于预设的扫描角度间隔,SS-MUSIC方法的峰值所对应的角度与实际角度有误差,且归一化功率分布不均衡。而本文方法估计的角度几乎与实际角度重合且归一化的功率都到了0.9以上,所以本文方法的估计性能要优于SS-MUSIC方法。

3.1.2 角度与距离估计分析

取K=3个窄带不相关的近场信号源,角度与距离分别为[-22.87°,25.42 m]、[25.19°,34.66 m]和[43.21°,59.18 m],先估计角度后并固定,用上述3种方法和ESPRIT方法对距离进行估计,得到估计距离与估计角度一一对应的仿真结果如图3所示。

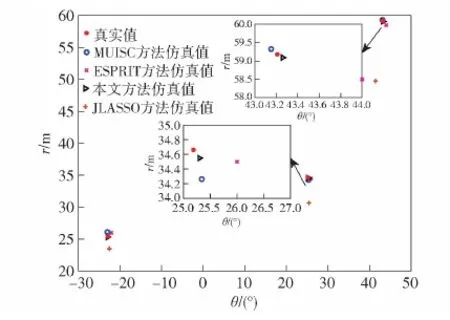
图3 角度与距离对应关系Fig.3 Relationship between angle and distance

从图3的仿真结果中可以看出,除了JLASSO方法对近场信号的距离估计失效之外,其余3种方法都能准确地估计出信号的位置。将实际信号位置细节进行放大,可以看到,ESPRIT方法估计出的信号位置误差最大,性能最差。本文方法与SS-MUSC方法都比较接近实际信号位置,其原因是SS-MUSIC方法与扫描角度间隔有关,但本文方法与实际信号位置的距离更接近,表现出的估计性能要优于上述3种方法。

3.2 估计精度性能分析

为了研究SNR和快拍数等因素和角度与距离之间的关系,把均方根误差(RMSE)作为精度的判别准则。定义均方根误差表达式为

(29)

(30)

式中:Q表示蒙特卡洛仿真实验的次数;qk表示第q次蒙特卡洛仿真实验估计的第k个信号入射角;qk表示第q次蒙特卡洛仿真实验估计的第k个信号距离。

3.2.1 RMSE随SNR变化

为了研究角度误差和距离误差随SNR的变化关系,在其他条件不变的情况下,设有一个近场信号,其入射角度与距离分别为[-22.87°,25.42 m],改变SNR从-10 dB开始,以步长2 dB增加到 10 dB,进行200次独立的蒙特卡洛仿真实验,得到仿真结果如图4所示。

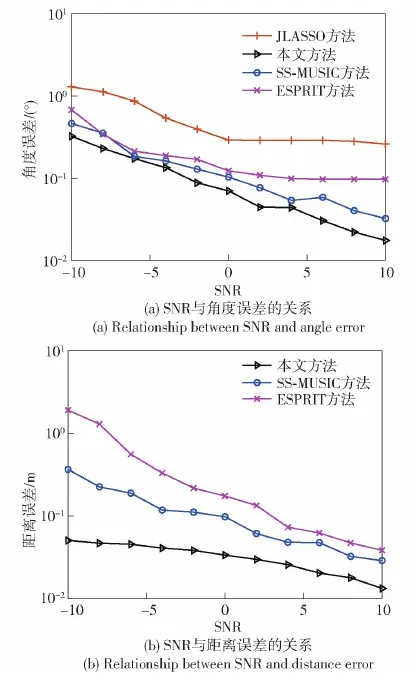
图4 不同SNR下的RMSE性能Fig.4 RMSE performance versus SNR of different methods

从图4(a)中可以看出,所有方法的角度误差都随SNR的增加而减少,但是JLASSO方法表现性能最差,角度误差较大,而SS-MUSIC方法得到的角度误差要小于ESPRIT方法,因此SS-MUSIC方法的性能优于ESPRIT方法。本文方法在整个SNR范围内角度误差小于上述3种方法,表现出了最优的估计性能。从图4(b)中可以看出,所有方法的距离误差都随SNR的增加而减少,在SNR整个区间,SS-MUSIC方法始终优于ESPRIT方法,本文方法在距离估计方面仍然表现出优良的估计能力,误差始终小于上述两种方法。仿真实验结果可以看出,本文方法具有稳定优良的DOA估计能力。

3.2.2 RMSE随快拍数变化

为了研究角度误差和距离误差随快拍数的变化关系,在其他条件不变的情况下,设有一个近场信号,其入射角度与距离分别为[-22.87°,25.42 m],改变信号快拍数从100开始,以步长100增加到1 000,进行200次独立的蒙特卡洛仿真实验,得到仿真结果如图5所示。

图5 不同快拍数各类方法的RMSE性能Fig.5 RMSE performances of different snapshot methods

从图5(a)中可以看出,所有方法的角度误差都随快拍数的增加而减少,但是JLASSO方法表现的角度误差变化缓慢,呈现的效果最差,而其他3种方法的表现性能提升很大,本文方法在整个快拍数范围内均能表现出较好的估计性能,误差始终小于SS-MUSIC方法和ESPRIT方法。从图5(b)中可以看出,所有方法的距离误差都随快拍数的增加而减少,在快拍数的整个区间,SS-MUSIC方法始终优于ESPRIT方法,本文方法在距离估计方面仍然给出了优良的估计能力,误差始终小于上述两种方法。从仿真实验结果可以看出,本文方法具有稳定优良的位置估计能力。

3.3 估计分辨力性能分析

为了研究SNR和快拍数等因素和角度分辨能力与距离分辨能力之间的关系,设有两个入射信号,定义分辨条件[24]:

max{|1-θ1|,|2-θ2|}<|θ2-θ1|/2

(31)

max{|1-r1|,|2-r2|}<|r2-r1|/2

(32)

固定θ1=0°,θ2=θ1+Δθ,Δθ是角度增量;1是真实角度r1的估计值;2是真实角度r2的估计值。固定r1=20 m,r2=r1+Δr,Δr是距离增量。固定两个信号源位置,其中信源1的位置为[0°,20 m],信源2的位置为[15°,35 m]。

3.3.1 角度分辨力

为了研究角度分辨力和距离分辨力误差随SNR的变化关系,在其他条件不变的情况下,固定信源1的位置,改变信号源2的入射角度,由1°增加到10°步长为1°。SNR快拍数分别为[0 dB,500]、[10 dB, 500]和[10 dB, 100],进行200次独立的蒙特卡洛仿真实验,得到准确率与角度间隔的仿真结果如图6所示。

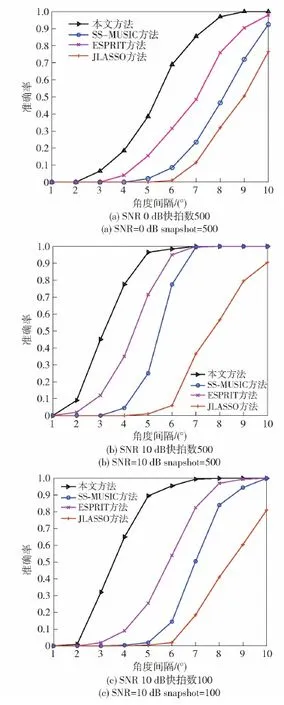
图6 角度分辨力变化Fig.6 Variation graph of angle resolution

从图6的变化曲线中可以看出,所有方法的准确率随角度间隔的增加都呈上升趋势。图6(a)和图6(b)中SNR分别设为0 dB和10 dB,快拍数都为500。SNR为0 dB时,本文方法成功估计出两个角度为9°,ESPRIT方法成功估计出两个角度为10°,SS-MUSIC方法在角度为10°时准确率接近0.95,而JLASSO方法在角度为10°时准确率接近0.75,本文提出的方法分辨率优于其他3种方法。SNR为10 dB时,本文方法,SS-MUSIC方法和ESPRIT方法成功估计出两个角度均为7°,而JLASSO方法在角度为10°时准确率接近0.9,随着SNR的增加,各类方法准确率都得到了提升;图6(b)和图6(c)中SNR都为10 dB,快拍数分别设为500和100。快拍数为100时,本文方法成功估计出两个角度为8°,ESPRIT方法成功估计出两个角度为9°,SS-MUSIC方法成功估计出两个角度为10°,而JLASSO方法在角度为10°时准确率接近0.8,快拍数为500时,本文方法,SS-MUSIC方法和ESPRIT方法成功估计出两个角度均为7°,而JLASSO方法在角度为10°时准确率接近0.9,说明随着快拍数的增加,各类方法准确率都得到了提升。

3.3.2 距离分辨力

为了研究角度分辨力和距离分辨力误差随快拍数的变化关系,在其他条件不变的情况下,固定信源1的位置,改变信号源2的距离,由21 m增加到30 m步长为1 m。进行了3次仿真实验,SNR快拍数分别为[0 dB,500]、[10 dB, 500]和[10 dB, 100],进行200次独立的蒙特卡洛仿真实验,得到仿真结果如图7所示。

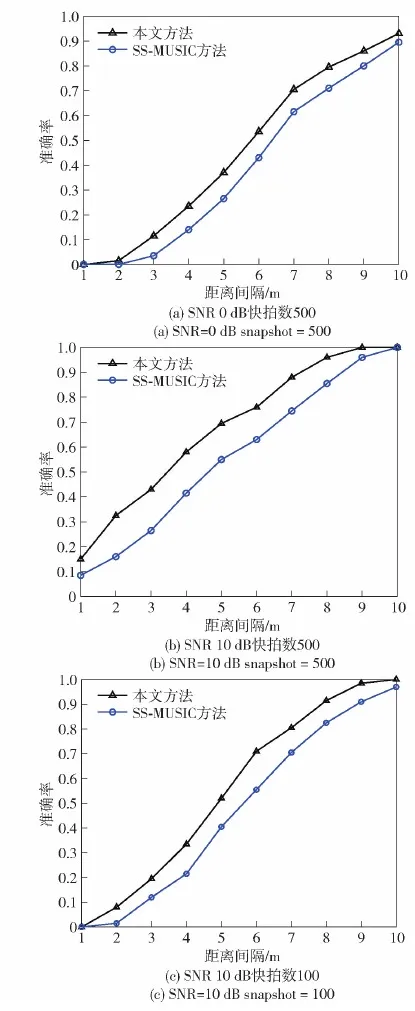
图7 距离分辨力变化曲线图Fig.7 Variation graph of distance resolution

从图7的变化曲线中可以看出,所有方法的准确率随距离间隔的增加都呈上升趋势,本文提出的方法优于SS-MUSIC方法。将图7(a)和图7(b)SNR分别为0 dB和10 dB,快拍数都为500。SNR为0 dB时,本文方法在距离为10 m时准确率接近0.93,SS-MUSIC方法在距离为10 m时准确率接近0.89。SNR为10 dB时,本文方法成功估计出两个距离为9 m,SS-MUSIC方法成功估计出两个距离为10 m,说明随着SNR的增加,各类方法准确率都得到了提升。将图7(b)和图7(c)图SNR都为10 dB,快拍数分别为500和100。快拍数为100时,本文方法成功估计出两个距离为10 m,SS-MUSIC方法在距离为10 m时准确率接近0.95;快拍数为500时,本文方法成功估计出两个距离为9 m,SS-MUSIC方法成功估计出两个距离为10 m。在其他距离间隔内准确率得到了提升,说明随着快拍数的增加,各类方法准确率都得到了提升。

4 结论

本文对压缩感知技术进行研究分析,利用该技术提出一种基于互质阵列的近场源位置估计方法。该方法预处理接收数据,得到了角度参数的求解模型,利用一种迭代方法来逐步修正角度偏移向量和功率向量,实现最终的DOA估计;将估计的DOA结果代入,建立关于距离参数的求解模型,利用梯度下降方法估计出距离。理论分析和仿真实验结果表明,本文方法在快拍数较少、SNR较低的情况下,依然可以获得比较好的位置估计性能,该方法不仅具有较高的估计精度,而且可以实现角度和距离参数的自动配对。本文处理角度网格和距离网格都需要使用梯度下降法,但梯度下降系数的选择比较困难,因此找寻一个自适应的梯度下降系数有待进一步研究。