基于频响特性的大起伏密集假目标干扰识别技术
2023-11-27韦文斌彭锐晖孙殿星张家林王向伟
韦文斌, 彭锐晖,2*, 孙殿星,3, 张家林, 王向伟
(1.哈尔滨工程大学 青岛创新发展基地, 山东 青岛 266000; 2.哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001;3.海军航空大学, 山东 烟台 264001)
0 引言
转发式密集假目标干扰是一种极具威胁的干扰样式,干扰机通过大量复制转发虚假回波,使其与真实目标回波具有高度的相干性,很难被有效识别,会产生大量的虚假点迹,严重影响雷达对目标的探测与跟踪[1-4]。其中,功率动态范围较大的密集假目标干扰(简称为大起伏密集假目标干扰)是指实际对抗中干扰机发射或雷达接收过程作用于天线主、副瓣等不同通道,导致干扰信号存在较大功率起伏,使得干扰信号具有干噪比变化大、特征提取不稳定等特点,给干扰识别带来了极大的挑战。目前国内外学者的研究主要是关注干扰功率相对稳定情况下的干扰信号识别,对大起伏密集假目标干扰信号识别的研究很少。文献[5-8]利用目标与干扰信号在时、空、频等域内的可分离性,对干扰进行了有效的识别与抑制,其中文献[5]利用干扰多普勒分布于有限范围内的规律特性,实现了干扰的识别与抑制,文献[6-7]利用自适应旁瓣对消的方法实现了干扰抑制,文献[8]利用帧间非相参累积和空域滤波实现了干扰抑制。经综合分析,上述文献均利用了目前干扰机计算资源和调制能力有限的特性,但随着干扰机计算资源与调制能力的日渐提升,密集假目标干扰与真实目标回波相似度不断提高,这些方法对目标和干扰的分离能力相对有限。文献[9-11]以特定体制雷达为工程应用背景,提出对抗密集假目标干扰的思路,其中文献[9]以阵列天线雷达为应用背景,提出基于盲源分离的方法实现密集假目标干扰的抑制,文献[10-11]以捷变频雷达为应用背景,分别联合Hough变换和波形熵对目标信息进行重构,其中Hough变换对计算资源要求较高。文献[12]通过设计调频斜率捷变线性调频(LFM)波形,对干扰参数进行重构,但其对该方法受信/干噪比影响程度没有进行明确的评估。近年来机器学习算法也被广泛引入于雷达干扰识别领域。文献[13]通过提取多维特征实现对密集假目标干扰的识别。文献[14-15]通过提取时频图作为特征,利用图像处理方法实现对密集假目标在内的多种干扰进行识别,其中文献[14]采用反向传播(BP)神经网络对干扰进行识别,文献[15]采用卷积神经网络对干扰进行识别,二者仅能对综合的干扰态势进行判别。文献[16]同样基于时频图特征,采用支持向量机(SVM)实现了对真、假目标的识别。文献[17]联合时频图与时相图,采用双分支卷积神经网络实现包括密集假目标干扰在内的多种干扰类型识别,然而实际相位特征对传播链路等因素变化极为敏感,可能导致性能不稳定现象。通过综合分析,文献[13-17]在信/干噪比较高条件下取得了良好效果,对于信/干噪比较低时,其性能退化比较明显。经对上述文献综合分析,针对密集假目标干扰的识别主要存在如下问题:欺骗干扰信号与目标回波高度相关,细微差异特征提取困难,难以对真、假目标有效识别;尤其现有干扰信号识别方法基本都是针对某个相对固定信/干噪比的情况,或某一相对较小的信噪比区间,而实际雷达接收到的回波(目标/干扰)强度通常具有较大的动态范围,尤其干扰信号从雷达不同的主/副瓣进入时,信/干噪比通常会具有较大的动态范围,针对该情况现有方法大多存在识别性能不稳定的问题。
针对上述问题,本文从密集假目标干扰产生机理和射频链路物理特性出发,提出基于雷达与干扰机频率响应特性(简称频响特性)差异的密集假目标干扰智能识别方法。首先,系统研究并提出了雷达与干扰机的频响特性差异及其对真、假目标回波信号幅频响应的影响机制模型;然后,构建多个相对独立的双通道特征融合一维卷积神经网络-长短时记忆网络(E-ODCNN-LSTM)算法作为基分类器,以实现信号特征的差异化提取,该算法通过一维卷积神经网络(ODCNN)上通道和长短时记忆网络(LSTM)下通道分别提取信号特征,将上下双通道所提取特征在特征融合层进行信息融合,实现信号特征的充分利用;最后,通过M/N逻辑准则综合集成,实现目标回波和密集假目标干扰信号的准确识别。仿真和实测数据测试,验证了该方法在较大信/干噪比动态范围下能够对干扰和回波进行有效和稳定的识别。
1 目标-干扰频响特征影响机制模型
1.1 DRFM干扰机与雷达频响特性分析
DRFM干扰机[18]系统通常包括上/下变频、模数转换(ADC)和数模转换(DAC)、功率放大、本振、控制等模块。以干扰信号产生为例,DRFM干扰机对雷达射频信号进行截获,经过下变频变换至中频后进行ADC,利用控制单元进行合适的干扰参数调制,经过数字滤波后经过DAC模块转换为模拟信号,最终经过中频放大、上变频、射频放大、发射天线等多个单元组成的发射链路,实现针对雷达信号参数的干扰信号产生。通过上述对干扰信号的产生机理进行分析可知:干扰信号的产生需要经过多个数字和模拟滤波以及多级功率放大环节,每一个环节物理器件的个性特征[19-21](本文主要是指频率响应特征,简称频响特征)都会对干扰信号产生不可忽略的影响,因此干扰信号上都会留下干扰机特有的烙印。特别地,对于一些模拟器件(滤波器和功率放大器等),由于制作工艺的限制,即使通过校准也不可能实现在其带内的绝对平坦,反而往往携带有显著而稳定的起伏特征,这些特征都会被由之产生的干扰信号所携带,从而为进行干扰信号识别研究提供稳定而可靠的信息。
与干扰机类似,雷达同样具备其特定的频响特性[22],但其工作体制与变频链路与干扰机存在一定差异,二者收发通道及其组成的物理器件频响特性必然存在差异,因此雷达与干扰机系统的综合频响特征必然存在较为鲜明的差异,这种内在的机理关系必然导致干扰机产生的密集假目标干扰与目标回波的频率响应特征(包括幅频响应特征和相频响应特征)存在较为鲜明的差异,从而为干扰识别提供可靠的理论依据[23-24]。
本文以LFM体制的S波段预警雷达为研究对象,在雷达发射信号调制带宽范围内,大气频响特性对信号传输过程中的幅频响应影响较小,且雷达工作频带通常选择在大气窗口内,因此LFM信号不同频率成分受大气幅频响应的影响可以忽略;而相位特征影响因素较多,如传输链路、距离变化等对相位特征的影响都不可忽略,基于相频响应特征的识别方法目前难以有效应用,因此本文主要从目标回波与干扰信号的幅频响应起伏特征差异对二者进行识别。
1.2 目标回波幅频响应影响机制模型
雷达系统可划分为收、发两个通道,如图1所示,为方便分析,将图中雷达收发通道内功率放大模块称为功率放大模块,其余模块统一称为通道电路模块。可以看出目标信号在入射前(以下简称目标入射信号,是指雷达发射信号辐射到目标上的信号)都需要经过滤波、DAC、上变频、功率放大、大气传输等多个环节的调制,每个环节都有其个性的频响特性。设图1中目标入射过程的滤波、DAC、上变频模块的组合频响为Hc1(f)(f表示频率),功率放大模块的频响为Hp1(f),大气传输的频响为Ha1(f);同理目标回波传播过程中也同样需要经过这些环节的调制,同样具备其特定的频响特性,假设Hc2(f)为该过程雷达滤波、ADC、下变频模块的组合频响,Hp2(f)为该过程雷达功率放大模块的频响,Ha2(f)为该过程大气传输的频响。图1中Hrc(f)表示雷达射频通道电路模块的频率响应,Hrc(f)=Hc1(f)Hc2(f),Hrp(f)表示雷达功率放大电路的频率响应,Hrp(f)=Hp1(f)Hp2(f)。
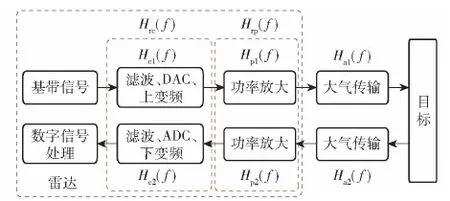
图1 目标回波频响特性物理模型Fig.1 Physical model of target echo frequency response characteristics
由上述分析及系统的级联特性可知,可将雷达系统各部分器件的频率响应表示为
Hr(f)=Hrc(f)Hrp(f)=Hc1(f)Hc2(f)Hp1(f)Hp2(f)
(1)
滤波器、功率放大器等器件的频率响应[20-21]可以表示为
H(f)=G(f)A(f)ejφ(f)
(2)
式中:G(f)为系统理想的频率响应;A(f)为幅频响应的非线性函数,A(f)=a0+ancos (2παnf),a0表示线性增益,an、αn表示起伏波动增益;φ(f)为相频响应的非线性函数。本文主要考虑幅频响应对信号的影响,为更好地拟合多器件综合情况下的高度非线性幅频响应特性,对A(f)进行重新定义[20-21]如下,使其能够适应较为复杂的情况:
A(f)=a0+ancos (2παnf)+bnsin (2πβnf)
(3)
式中:bn和βn表示起伏波动增益。则可将雷达系统的频率响应表示为
Hr(f)=Gr(f)Ar(f)ejφr(f)=Gr(f)[a0+ancos (2παnf)+bnsin (2πβnf)]ejφr(f)
(4)
式中:Gr(f)为雷达系统理想的频率响应;Ar(f)为雷达系统幅频响应的非线性函数;φr(f)为雷达系统相频响应的非线性函数。设雷达发射信号的频谱为S(f),目标回波信号传输过程的能量衰减系数为a,则回波信号频响St(f)可表示为
St(f)=aAtS(f)Hr(f)+Nt(f)
(5)
式中:At为目标回波强度系数;Nt(f)为噪声频谱。(5)式表明目标回波信噪比取决于At的大小,当At动态范围较大时,目标回波的信噪比动态范围也较大,设目标回波的幅频响应为At(f):
At(f)=|St(f)|=|aAtS(f)Hr(f)+Nt(f)|= |aAtS(f)Gr(f)Ar(f)ejφr(f)+Nt(f)|= |aAtS(f)Gr(f)[a0+ancos (2παnf)+bnsin (2πβnf)]ejφr(f)+Nt(f)|
(6)
1.3 干扰信号幅频响应影响机制模型
与目标回波频响分析过程类似,但干扰信号叠加了干扰机特有的频响特征,如图2所示,干扰机系统同样具有收发两通道。为方便分析,图中给出了各个模块频响及组合频响,Hp3(f)为干扰机接收通道功率放大模块的频响,Hc3(f)为干扰机接收通道滤波、ADC、下变频模块的组合频响,Hp4(f)为干扰机发射通道功率放大模块的频响,Hc4(f)为干扰机发射通道滤波、DAC、上变频模块的组合频响,Hjc(f)表示干扰机通道电路模块的频率响应,Hjp(f)表示干扰机功率放大电路的频率响应。
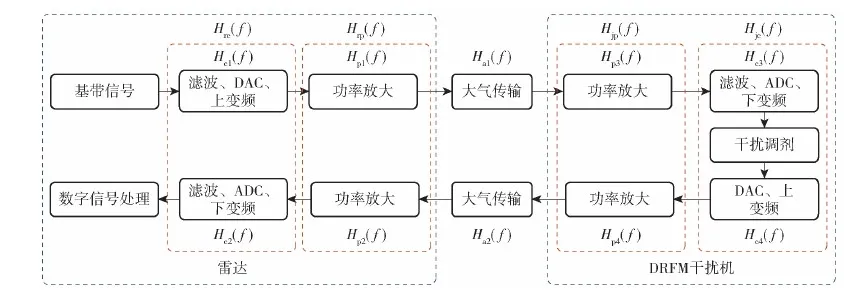
图2 干扰信号频响特性物理模型Fig.2 Physical model of jamming signal frequency response characteristics
如图2所示,由系统级联特性可将干扰机系统各器件的频率响应表示为
Hj(f)=Hjp(f)Hjc(f)=
Hc3(f)Hc4(f)Hp3(f)Hp4(f)
(7)
式中:Hjp(f)=Hp3(f)Hp4(f);Hjc(f)=Hc3(f)Hc4(f)。
由于干扰信号同时受到雷达与干扰机系统频率响应的影响,可将二者复合系统的频率响应表示为
Hrj(f)=Hrc(f)Hrp(f)Hjc(f)Hjp(f)=Hc1(f)Hc2(f)Hc3(f)Hc4(f)Hp1(f)·Hp2(f)Hp3(f)Hp4(f)
(8)
考虑系统内各器件的非线性特性,也可将Hrj(f)近似建模为三角函数[20-21],即
Hrj(f)=Grj(f)Arj(f)ejφrj(f)=Grj(f)[a0+ancos (2παnf)+bnsin (2πβnf)]ejφrj(f)
(9)
式中:Grj(f)为复合系统理想的频率响应;Arj(f)为复合系统幅频响应的非线性函数;φrj(f)为复合系统相频响应的非线性函数。假设干扰信号传输过程能量衰减系数为b,则干扰信号频响可表示为
Sj(f)=bAjS(f)Hrj(f)+Nj(f)
(10)
式中:Aj为干扰信号强度系数;Nj(f)为噪声频谱。在干扰过程中由于雷达-干扰天线对准、功率控制、位置关系等多种因素的动态变化会使干扰信号存在较大的起伏,即导致干噪比的动态范围较大。最后,可将干扰信号的幅频响应Aj(f)表示为
Aj(f)=|Sj(f)|=|bAjS(f)Hrj(f)+Nj(f)|= |bAjS(f)Grj(f)Arj(f)ejφrj(f)+Nj(f)|= |bAjS(f)Grj(f)[a0+ancos (2παnf)+bnsin (2πβnf)]ejφrj(f)+Nj(f)|
(11)
与At(f)相比,Aj(f)还受到干扰机两个模块频响Hjc(f)和Hjp(f)的调制,因此其起伏特性必然与目标回波的幅频响应存在较大差异,此特征差异为进行目标-干扰的辨识提供了现实可行的依据。
2 目标-干扰特征提取与识别方法
2.1 目标回波幅频响应起伏特征提取
根据1.2节所述过程,对目标回波幅频响应特征进行提取,假设LFM信号载频为f0,调频斜率为μ,脉冲宽度为T,则雷达发射信号模型为
(12)
根据式(12),LFM信号复包络为
(13)
故雷达发射信号的频谱为
(14)
(15)
c(-v)=-c(v),s(-v)=-s(v)
(16)
将式(14)化简,得到雷达发射信号频谱为
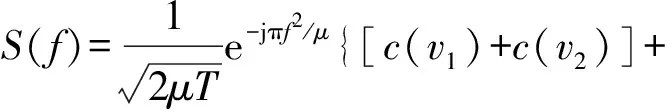
(17)
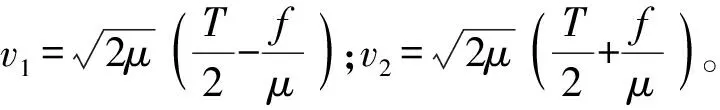
以上均为理想的分析过程,但如1.1节所述,由于雷达系统特性,雷达发射信号频谱不可能做到理想状态,因而以下对实际情况进行分析,为了具有实际泛化意义,对式(12)中LFM信号进行快速傅里叶变换,求取其离散频谱S(fn),得
S(fn)=FFT[s(t)]=[V(f1),V(f2),…,V(fM)]
(18)
式中:V(fn)表示频率为fn时的频谱样本分量,n=1,2,…,M,M为快速傅里叶变换的点数。依据式(4)所建立雷达系统频响模型,对其进行离散处理得到Hr(fn),即
Hr(fn)=[Wr(f1),Wr(f2), …,Wr(fM)]
(19)
式中:Wr(fn)表示频率为fn时雷达系统的频响分量。则目标回波信号频谱在经过雷达系统频响调制后,其频谱样本向量St(fn)为
St(fn)=aAtS(fn)⊙Hr(fn)+Nt(fn)=aAt[V(f1)Wr(f1),V(f2)Wr(f2),…,V(fM)Wr(fM)]+Nt(fn)
(20)
式中:⊙为哈达玛积运算符号。因此目标回波的幅频响应Ar(fn)为
Ar(fn)=|St(fn)|=|aAtS(fn)⊙Hr(fn)+Nt(fn)|= |aAt[V(f1)Wr(f1),V(f2)Wr(f2),…,V(fM)Wr(fM)]+Nt(fn)|
(21)
At(fn)蕴含了目标回波由于雷达系统频响调制所产生的幅频响应起伏特征。由于实际中回波信号受雷达天线方向图,目标雷达散射截面(RCS)起伏等因素影响,都会使得目标回波具有较大的功率动态范围。为消除功率绝对大小对识别性能的影响,需要对接收的目标回波进行最大值归一化处理,首先采用峰值搜索,查找目标回波幅频响应的最大分量At(fmax),则目标回波幅频响应最大值归一化结果为
(22)
基于式(22),便得到了目标回波幅频响应特征模型,由于噪声强度相对固定,当Ar取值不同时,目标回波信噪比也不同,其幅频响应特征中蕴含的信号和噪声特征成分比例也不同,因此即使对于目标回波而言,其幅频响应特征在不同信噪比下也存在较大差异,故当At动态范围较大时,目标/干扰的信(干)噪比动态范围较大,对于目标-干扰信号的识别难度也大大增加。
2.2 干扰信号幅频响应起伏特征提取
本文所提取的幅频响应起伏特征不受干扰信号多普勒、时延调制的影响,由于假目标干扰信号由干扰机对截获的雷达信号进行幅度、时延和多普勒调制-转发形成,根据傅里叶变换性质,干扰信号理想状态下的频谱可由雷达发射信号的频谱得到,即
Sj(f)=AmS(f-fm)e-j2πftm
(23)
式中:Am、tm、fm分别为第m个干扰的幅度、时延和多普勒调制系数。与目标回波类似,对式(9)所建立的雷达与干扰机系统复合频响进行离散处理,得
Hrj(fn)=[Wrj(f1),Wrj(f2),…,Wrj(fM)]
(24)
式中:Wrj(fn)为频率为fn时雷达与干扰机系统幅频响应分量。故干扰信号的频谱样本向量为
Sj(fn)=bAjS(fn)⊙Hrj(fn)+Nj(fn)=bAj[V(f1)Wrj(f1),V(f2)Wrj(f2),…,V(fM)Wrj(fM)]+Nj(fn)
(25)
则干扰信号的幅频响应Aj(fn)为
Aj(fn)=|Sj(fn)|=|bAjS(fn)⊙Hrj(fn)+Nj(fn)|= |bAj[V(f1)Wrj(f1),V(f2)Wrj(f2),…,V(fM)Wrj(fM)]+Nj(fn)|
(26)
同理,Aj(fn)中即蕴含了干扰信号由于雷达与干扰机频响调制所产生的幅频响应起伏特征,采用峰值搜索算法,求取其最大分量Aj(fmax),得到最大值归一化结果为
(27)
基于式(27),便得到了干扰信号幅频响应特征模型。同理,当Aj大小不同时,干扰信号的干噪比不同,其幅频响应特征中蕴含的噪声特征比例成分也不同,由于干扰信号可能从雷达的不同主/副瓣进入接收机,Aj通常具有较大的动态范围,从而使干扰信号具有不同的干噪比特征,因此实际干扰信号的幅频响应特征受噪声特征影响程度差异也较大。因而对于干扰信号而言,其不同干噪比下的幅频响应特征也存在较大差异,导致了信/干噪比动态范围较大情况下目标-干扰信号的识别难度较大。
2.3 目标-干扰识别算法
基于2.2节和2.3节的分析,提出一种E-ODCNN-LSTM双通道特征融合算法,其中单个算法主要包括3个部分:上通道层、下通道层和特征融合层。上通道层由ODCNN构成,ODCNN[26]常用于解决一维序列问题,能够很好地适应本文一维幅频响应特征提取;下通道由LSTM构成,LSTM是一种改进的RNN,其通过遗忘门、输入门和输出门,实现对隐含层输入、输出等状态信息的有效控制,可以很好提取信号脉冲幅频响应信息;特征融合层主要由全连接层和激活函数构成,将上通道和下通道所提取的信号特征进行Flatten处理后,在全连接层进行Concatenate拼接,进而利用激活函数实现融合特征的非线性映射,对信号两个维度特征进行充分利用,最后对融合特征进行分类。同时,本文考虑在信/干噪比动态范围较大情况下的目标-干扰识别问题,由于不同信/干噪比条件下,目标回波与干扰信号的幅频响应特征受噪声特征影响程度不同,样本具有多样性,仅依靠单一分类器不能完全将所有样本特征进行合理映射,容易陷入局部最优解的情况,无法保证识别的准确性和稳定性。因此,本文考虑将双通道ODCNN-LSTM作为基础分类器,通过将多个基分类器集成,构建E-ODCNN-LSTM算法,利用各个基分类器在训练过程中所具有的相对独立性,以及对不同信/干噪比样本的侧重性,较好的解决了陷入局部最优解的困境,做到信息的补偿和强化,通过M/N逻辑准则集成的方式提高识别的准确性和稳定性。经过仿真与实测数据实验验证,随着基分类器个数越多,集成算法的识别性能越高,但当基分类器个数达到一定数量后,算法的识别性能趋于稳定,但此时伴随着时耗增大的问题,因此综合考虑算法的识别性能与计算资源开销,将基分类器个数确定为9个。考虑本文所提取的特征维数以及训练样本数量不大,选择深度网络可能导致梯度发散或消失问题,同时结合时效性能考虑,本文在对每一个基分类器的参数选择上较为保守。
综合以上分析,本文的干扰识别算法流程如图3所示,图中S1~S9分别表示9个基ODCNN-LSTM分类器,具体步骤如下:
1)雷达接收信号快速傅里叶变换计算;
2)求取雷达接收信号幅频响应;
3)峰值搜索,求取雷达接收信号幅频响应最大分量;
4)雷达接收信号幅频响应最大值归一化处理;
5)基分类器网络参数设置,综合考虑算法的识别性能和计算资源开销,选择9个基分类器进行集成,网络参数设置如下:为实现不同感受野和提取不同分辨率情况下的频响特征,9个上通道ODCNN算法中,其中3个算法卷积核长度为6,3个算法的卷积核长度为8,剩余3个算法的卷积核长度为10,同时各个算法均采用3层卷积层和池化层提取特征,卷积步长均为1,padding=‘same’,Flatten层数为1;下通道LSTM算法层数为4,输入特征维数为 1 024,隐含特征维数为128,特征融合层后特征维数为640,Flatten层数为1,全连接层1输入特征维数为640,全连接层数2输入特征维数为64,激活函数选择ReLU。
6)将待预测的雷达接收信号幅频响应特征作为基分类器输入特征,基分类器间并行完成特征提取与融合处理,保证各基分类器所提取特征具有相对独立性,最后实现各个基分类器识别;
7)将9个基分类器采用M/N逻辑准则的方式集成,实现最终目标-干扰分类识别。
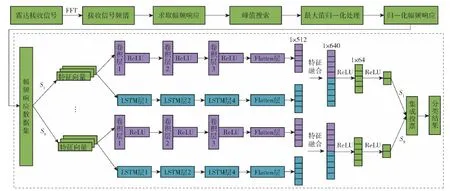
图3 目标-干扰信号识别算法流程Fig.3 Target-jamming signal recognition algorithm
3 实验与分析
为验证本文方法的有效性,设置以下仿真实验进行验证,为方便对后续识别实验进行定量分析,首先对雷达与干扰机的幅频响应曲线的模型进行仿真;其次设置单一信/干噪比条件下识别效果仿真实验,其中包括3个子实验,分别测试3种干信比条件下本文方法在单一信/干噪比情况下的识别结果;设置大起伏密集假目标干扰信号识别效果仿真实验,测试本文方法对大起伏密集假目标干扰的识别效果;设置不同网络模型识别效果仿真对比实验,测试本文模型方法在不同信噪比中心值情况下对大起伏密集假目标干扰的识别效果,同时对最佳分类器个数进行验证和描述;设置实测数据验证实验,对本文方法进行有效性验证;最后设置3组对比实验,其中单一信/干噪比条件下仿真对比实验包含两个子实验,主要验证单一信/干噪比情况下本文方法的优越性,大起伏密集假目标干扰仿真对比实验,验证大起伏信/干噪比条件下本文方法的优越性。仿真实验所用的目标回波和干扰信号的参数如表1所示。
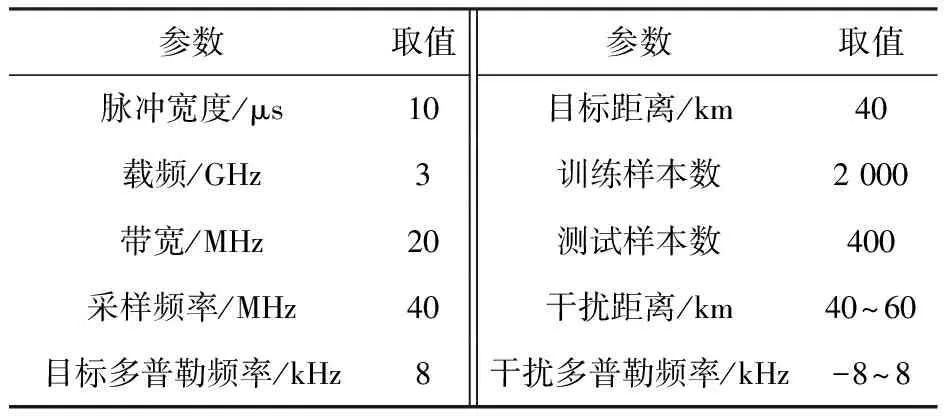
表1 仿真参数设置Table 1 Parameter setting for simulation
3.1 雷达与干扰机综合幅频响应仿真
为方便定量分析,首先需要对雷达和干扰机的幅频响应曲线进行仿真。选取式(3)三角函数模型对雷达与干扰机的幅频响应A(f)进行仿真建模,由于物理器件的差异,不同物理器件的幅频响应存在差异,其可以用不同的系数进行模拟,对于本文方法验证,不失一般性分别设置两组[a0,an,αn,bn,βn]系数为[10,0.6,6,0.4,4]和[10,0.3,9,0.7,5]代表雷达与干扰机的幅频响应特性[20-21]。幅频响应离散点数为1 024,起伏中心均为20 dB,起伏范围均为±0.8 dB。幅频响应仿真结果如图4所示,可以看出:雷达与干扰机综合幅频响应曲线的起伏趋势存在较为明显的差异,如2.1节所述,这种差异是由收发通道物理特性所决定的,本文即基于此特性差异对目标回波和欺骗干扰信号进行识别。
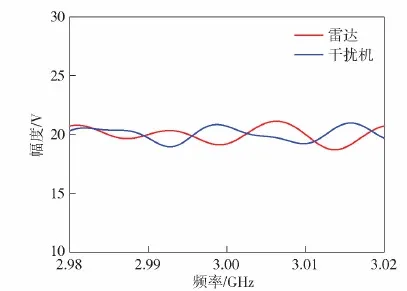
图4 幅频响应曲线仿真模型Fig.4 Simulation model of amplitude frequency response curves
3.2 单一信/干噪比条件下识别效果仿真实验
鉴于目前国内外学者主要集中于单一信/干噪比条件下对干扰进行识别研究,本文首先仿真测试基于本文提出的真-假目标频响特征差异,利用 E-ODCNN-LSTM算法在单一信/干噪比条件下的识别性能,并与单一算法识别结果进行比较,考虑通常情况下干扰信号通常具有较高的干信比,本文实验主要针对3种不同干信比的情况进行测试。基于 3.1节对雷达与干扰机综合幅频响应的仿真算法,以及式(22)和式(27)建立的目标回波和密集假目标干扰信号幅频响应特征提取算法,分别对目标回波与干扰信号进行2 400次蒙特卡洛仿真实验,其中2 000次结果用于网络训练,通过调整式(21)和式(26)中目标回波和干扰信号强度系数,3种干信比依次为0 dB、3 dB、5 dB,对应的仿真结果分别如图5、图6、图7所示。图5~图7中整体正确识别率为 400个目标和400个干扰样本的整体正确识别率,即800个样本的正确识别率;目标错误识别率为400个目标样本中被误识别为干扰信号所占比例;干扰错误识别率则为400个干扰样本中被误识别为目标回波所占比例。考虑到不同干信比条件下,识别难度不同,因而每次仿真测试中信噪比范围存在一定变化,3次测试结果的信噪比跨度范围为-14~20 dB,每次测试中信噪比每隔2 dB进行一次识别效果实验,取50次识别结果平均值作为最终识别结果。
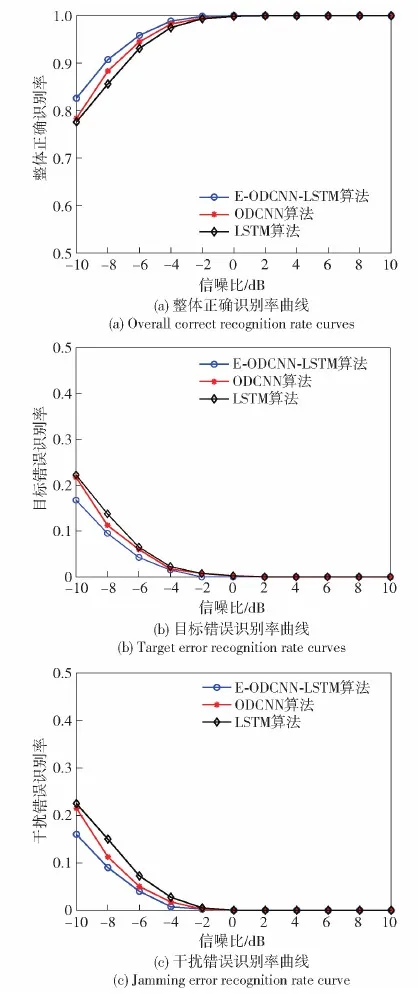
图6 干信比为3 dB仿真识别结果Fig.6 Simulation recognition results with JSR=3 dB
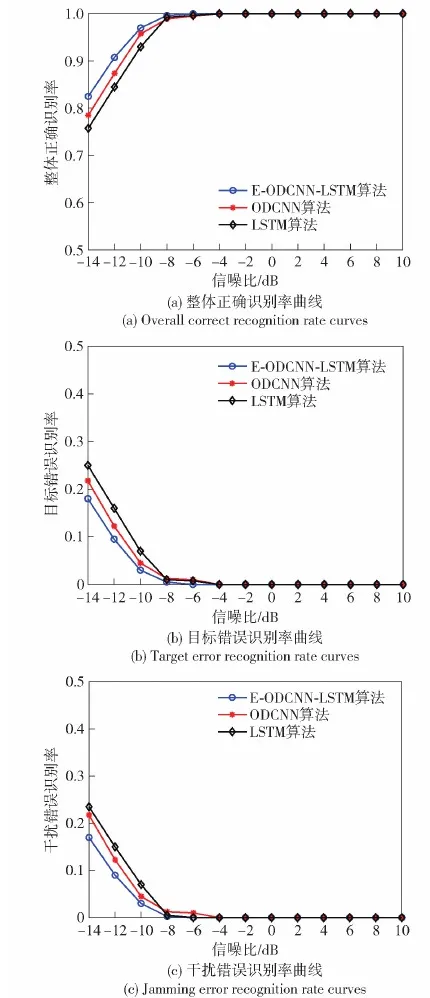
图7 干信比为5 dB仿真识别结果Fig.7 Simulation recognition results with JSR=5 dB
如图5所示,在干信比为0 dB时,当信噪比大于0 dB后E-ODCNN-LSTM算法的正确识别率达到82%以上,并且相对单一的ODCNN或是LSTM算法优势较为明显。当信噪比小于6 dB时,E-ODCNN-LSTM算法相对ODCNN而言,在各个信噪比条件下正确识别率有约2.0%~4.5%的提升,而相对于LSTM其性能提升更为明显,正确识别率有约4.5%~9%的提升,并且信噪比越低,其识别性能提升越明显。同时E-ODCNN-LSTM算法对目标和干扰的错误识别率,相对其他两种算法而言,也有一定程度的下降。由于当干信比为0 dB时,干扰信号与目标回波的功率相同,二者的幅频响应特征受噪声影响程度相当,此时相关程度最高,当信噪比较低时,噪声成分所占比重较大,其识别难度最高。
如图6所示,当干信比提升为3 dB后,干扰与回波的频响特性差异能够更好地凸显出来,因此 3种网络算法的识别性能均显著提升。当信噪比等于-8 dB时,E-ODCNN-LSTM算法的正确识别率达到90%以上,同时在各个信噪比条件下,相对于单个ODCNN算法均有提升,尤其当信噪比小于-6 dB时,性能提升最为明显,提升效果约为1.5%~4%;相较于LSTM有约2.5%~5%的提升。
如图7所示,当干信比提升为5 dB后,3种网络算法的识别性能进一步提升,对于E-ODCNN-LSTM算法,在信噪比等于-10 dB时,正确识别率大于97%,相较其他两种算法存在较为明显的优势,特别地,在低信噪比情况下,相较单个ODCNN算法和LSTM算法,正确识别率分别有1.5%~4%和4%~7%的提升。综合以上测试,可以看出:在信噪比较低时,E-ODCNN-LSTM算法所表现的性能相对单个ODCNN算法和LSTM算法而言更为优越。这主要是因为:在信噪比较低时,目标回波与干扰信号的幅频响应特征包含的噪声特征成分较多,识别难度增大,单个算法识别稳定性较差,而结合双通道特征融合算法后,可以充分利用ODCNN和LSTM提取的信号频响特征信息,更好地挖掘信号之间的差异;其次将基分类器进行集成,利用多个基分类器实现决策融合,一定程度上实现信息的补充和强化,可以实现识别稳定性的提升;最后由于单个算法在训练时容易陷入局部最优的情况,多个算法集成后使得陷入局部最优的情况有所改善,从而实现更为优越性能。
3.3 大起伏密集假目标干扰信号识别效果仿真实验
考虑目前缺少针对大起伏密集假目标干扰信号进行识别的研究成果,而实际情况中,目标回波和干扰信号的功率通常具有较大的动态范围,即现实中目标回波和干扰信号的信/干噪比具有较大的动态范围,使得目标-干扰信号的幅频响应起伏特征中噪声特征比重也存在较大差异,使得真、假目标的识别难度大大增加。针对这一现实难题,本实验结合E-ODCNN-LSTM算法的优势,针对大起伏密集假目标干扰的情况进行仿真验证,并与单个ODCNN算法以及LSTM算法的识别情况进行比较。改变 3.2节中仿真条件,生成信噪比均匀分布于-10~10 dB之间的2 400个目标回波样本,信噪比跨度范围为20 dB,信噪比中心值为0 dB,其中2 000个样本用于训练,其余400个样本用于测试;同时生成干噪比均匀分布于-10 ~10 dB之间的2 400个干扰信号样本,干噪比跨度范围为20 dB,干噪比中心也为0 dB,其训练集和测试的划分方式与目标回波相同。改变干扰信号的强度系数,使干扰信号的干噪比中心逐渐增大(如干噪比中心为2 dB时,代表干扰信号样本的干噪比均匀分布于-8~12 dB之间),针对不同整体干信比(整体干信比定义为干扰信号的干噪比中心与目标回波的信噪比中心值的差值)情况进行仿真测试,仿真结果如图8所示。

图8 信噪比为-10~10 dB动态范围情况仿真识别结果Fig.8 Simulation and recognition results of dynamic range with SNR=-10-10 dB
由图8可知,相对单一信/干噪比情况下的识别问题,大起伏信/干噪情况下的识别难度明显增大,尤其在整体干信比小于4 dB时,单个ODCNN算法和LSTM算法的性能下降较为明显,而E-ODCNN-LSTM算法相对还能保持较高的识别率。尤其当整体干信比小于10 dB时,E-ODCNN-LSTM算法的性能优势相对较为明显,相对单个ODCNN算法和LSTM算法,正确识别率分别有约1%~5%和1%~6%的提升,即整体干信比越低,识别难度越大时,E-ODCNN-LSTM算法的性能优势越明显。
3.4 不同网络模型识别效果仿真对比实验
本实验主要针对不同信噪比动态中心值的情况将3种集成算法以及ODCNN和LSTM算法的性能进行对比,主要测试基分类器个数对集成算法性能的影响。3种集成算法的基分类器个数不同,其中E-ODCNN-LSTM1为本文所设计的采用9个基础分类器算法,而E-ODCNN-LSTM2和E-ODCNN-LSTM3算法分别采用15个和5个基础分类器。本次试验样本数量与划分情况与3.3节相同,设置整体干信比为6 dB,信噪比动态范围中心值依次选择-5 dB、0 dB、5 dB,信/干噪比动态范围为20 dB,仿真结果如图9所示。
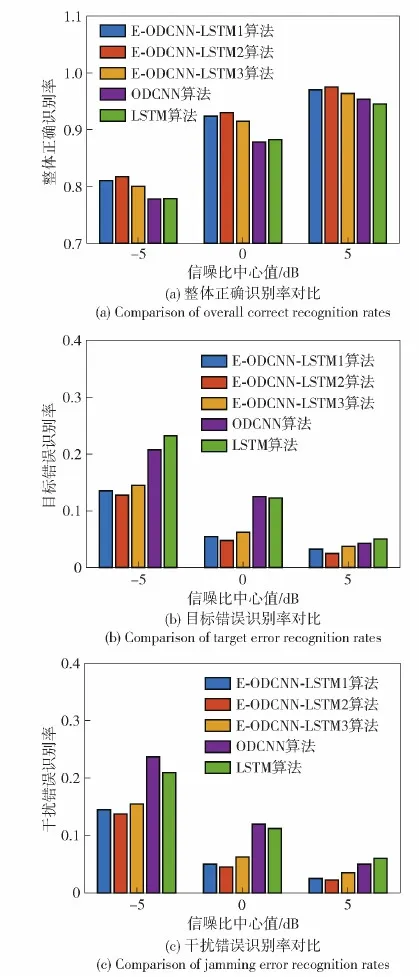
图9 不同信噪比动态范围中心值下5种算法性能对比Fig.9 Performance comparison of five algorithms with SNR dynamic ranges of different center values
从仿真结果中可见:在各个信噪比中心值,采用15个基础分类器的E-ODCNN-LSTM2算法的识别性能最高,本文所设计的E-ODCNN-LSTM1算法次之,而采用5个基础分类器的E-ODCNN-LSTM3算法在3种集成算法中效果最差。此外在3种集成算法中,9个分类器的E-ODCNN-LSTM1算法相对5个分类器的E-ODCNN-LSTM3算法性能提升相对较大,而15个分类器的E-ODCNN-LSTM2算法相对 9个分类器的E-ODCNN-LSTM1算法性能提升相对较小。这说明当基分类器个数达到一定数量后,继续增加基分类器个数对于提升算法性能有限,而当基分类器个数较大时,算法的计算量增大,会占用较多的计算资源,增加了计算成本,因此综合考虑算法的识别性能和开销成本,本文采用9个基分类器的集成E-ODCNN-LSTM1算法较为合适。并且其性能相对其他两种单独分类器算法而言性能都有较大提升,尤其当信噪比动态范围中心为-5和0 dB时,E-ODCNN-LSTM1算法相对其他两种单独分类器算法均有3%以上的提升,效果较为明显。
综合3.3节仿真实验2和本节仿真实验结果,可以看出:E-ODCNN-LSTM算法相对单个算法而言,无论正确识别概率,还是目标/干扰的错误识别概率都有较大的改善,这主要是因为:首先,由于双通道特征融合E-ODCNN-LSTM算法的上下通道能够分别提取信号的频响信息,相对单一算法而言,能够进一步挖掘信号的细节信息,因此相对单一算法具有更高的识别率;其次,对于集成算法,各个基分类器在训练过程中具有一定的独立性,可以实现特征的差异化映射,从而作出不同的判决效果,将各个基分类器进行决策融合后,其作出的判决结果更为可靠,可以纠正部分误判结果,因此其识别率有所提升;最后,是因为样本中的信/干噪比动态范围较大,即样本具有多样性,各个基分类器在训练时会各有侧重地倾向于某一个信/干噪比范围内的样本,从而在最终投票时,将各个分类器的优势综合,实现信息的补偿和强化,最终实现比单个分类器更好的效果。虽然通过基分类器集成能够实现性能的提升,但是并不意味着,可以通过增加基分类器个数无限提升集成算法的性能,这主要是因为基分类器获取的信息终是有限的,当基分类器个数达到一定数量后,信息挖掘和强化的效果已经达到上限,无法继续上升。
3.5 实测数据验证实验
利用某型雷达的实测数据对本文方法进行测试,其频点处于X波段,带宽为20 MHz,随机选取干扰和回波脉冲各1 280个,训练集与测试集划分比例为3∶1,经估算采集的目标回波和干扰信号的信/干噪比大致分布于-12.6~10.5 dB之间。本次识别结果如下:整体正确识别率为94.7%,目标正确识别率约为95%,干扰正确识别率约为94.4%。由于在实测数据中,雷达与干扰机的频响曲线起伏差异较大,因此其识别效果要优于仿真实验。这也进一步验证了:在雷达与干扰机的频响曲线起伏特征更鲜明时,识别难度会降低。由于实测数据的敏感性,在本文中只展示部分样本,图10为近似相同信/干噪比情况下目标回波和干扰信号的归一化幅频响应,可以看出二者的起伏趋势明显不同,其中干扰信号的频响由于受到干扰机的调制,幅频响应起伏更为明显,这表现为具有更多毛刺。

图10 实测样本幅频响应Fig.10 Amplitude frequency response of the measured sample
3.6 单一信/干噪比条件下仿真对比实验
本节包括两个子实验,首先,将本文方法与目前国内外多数学者关注的单一信/干噪比条件下的干扰识别成果进行对比。由于3.2节~3.4节仿真实验采用的训练样本数量与文献[16]不同,故单独进行仿真对比测试。保持3.2节仿真实验1(干信比为0 dB时)其他条件不变,仅改变蒙特卡洛仿真次数,使目标与干扰训练样本个数各为100个,使本次对比实验的仿真条件与文献[16]相同。测试结果如图11,从图中可以看出,本文方法在信噪比较低时,识别性能远远高于文献[16],充分说明本文提取的幅频响应起伏特征在目标回波与干扰信号功率相当、脉内特征相似时,对干扰信号的识别性能更好,低信噪比条件下的稳定性也更高;同时本文所用的E-ODCNN-LSTM算法也比经典的SVM算法更具优势,能够更深层次的提取信号特征。另外,与 3.2节 2 000个训练样本结果相比,本次实验识别效果下降并不大,说明本文算法在样本较少时,也具有一定的稳定性。
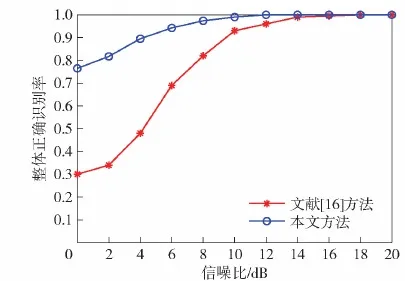
图11 本文方法与文献[16]方法对比结果Fig.11 Comparison between our method and the method in Ref.[16]
文献[17]采用卷积神经网络对干扰进行识别,将本文方法与文献[17]进行对比,保持3.2节仿真实验1其他条件不变,使本次实验中干信比为6 dB,以及目标回波和干扰信号训练样本个数各为600个。对比结果如图12所示,可以看出本文方法在文献[17]仿真条件下,无论目标正确识别率还是干扰正确识别率,在各个信噪比条件下均能实现100%的正确识别率,相较于文献[17]更具优势。
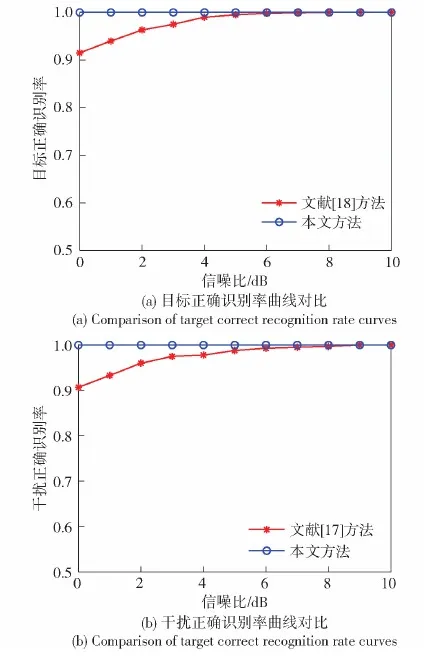
图12 本文方法与文献[17]方法对比结果Fig.12 Comparison between our method and the method in Ref.[17]
3.7 大起伏密集假目标干扰仿真对比实验
为说明在大起伏密集假目标情况下本文所提方法的优势,本实验通过提取文献[27]所用的时域偏度、峰度、包络起伏度等特征,将其用于大起伏密集假目标干扰的识别。保持3.3节仿真实验2条件不变,使信/干噪比跨度范围为20 dB,对比结果如表2所示。由表2可以看出,文献[27]方法的识别率仅能维持在65%左右,并且随着信噪比中心值的提高,其识别性能提升也较为缓慢;而本文所提方法,在各个信噪比中心值下的正确识别率均远高于对比文献[27]方法的识别率,并且随着信噪比中心值的提高,本文方法的正确识别率显著提升,说明本文方法相对传统方法而言,在针对大起伏密集假目标干扰的情况时具有较大优势。
4 结论
本文从雷达与干扰机的射频链路物理特性出发,通过建立目标回波和干扰信号频响机制影响算法,进而提出了基于雷达与干扰机频率响应特性差异的信/干噪比大动态范围变化条件下的密集假目标干扰识别方法。通过幅频响应特征的提取和 E-ODCNN-LSTM网络算法的构建实现干扰-回波信号的有效识别,实现了密集假目标干扰与目标回波信号的细微特征提取,信/干噪比大范围动态变化条件下目标/干扰信号特征起伏敏感、识别性能不稳定的难题。实现了干信比为0 dB、3 dB、5 dB共3种下对干扰的稳定识别,当信噪比大于10 dB时,均能实现100%正确识别;信噪比-10~10 dB动态范围下,对全体目标-干扰信号的稳定识别,当整体干信比大于6 dB时,整体识别率高于91%;当实测数据信/干噪比动态大致分布于-12.6~10.5 dB时,正确识别率高于94.5%;最后与经典文献方法进行对比,体现了本文方法的优越性。
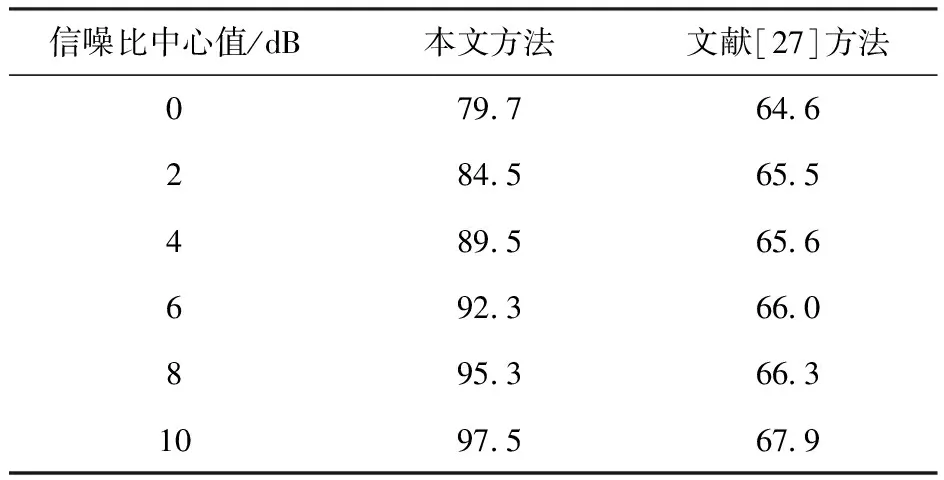
表2 大起伏条件下识别结果对比Table 2 Comparison of recognition results under large fluctuation conditions %
