互耦条件下涡旋电磁波目标方位探测方法
2023-11-27章鸿运栗苹李国林贾瑞丽
章鸿运, 栗苹, 李国林, 贾瑞丽
(北京理工大学 机电动态控制重点实验室, 北京 100081)
0 引言
近年来,携带轨道角动量(OAM)的涡旋电磁波被广泛应用于雷达[1]、通信[2]和6G无线网络[3]中。电磁波的总角动量可以分解为自旋角动量和OAM,携带不同OAM模式数的电磁波之间是正交的,这为模分复用多输入多输出(MIMO)系统提供了理论基础[4]。电磁波的OAM信息在可见光波段具有较为成熟的应用。直到2007年涡旋电磁波才首次被引入微波波段中[5]。随后,使用均匀圆环阵列产生涡旋电磁波的方法被广泛采用[6]。
与传统电磁波不同,涡旋电磁波的波前呈螺旋形分布,提供了方位分辨所需的相位变化。不同模式涡旋电磁波的相位分布不同,实现了对角度的分集,还具备一定的抗干扰能力。采用均匀圆阵发射携带不同OAM模式数的涡旋电磁波,对接收回波进行处理时,目标方位信息可以通过模式数与目标方位角之间的对偶关系获得。文献[7]通过对回波信号OAM域做傅里叶变换,获得目标的方位角信息。紧接着空间谱估计的方法被引入涡旋电磁波探测中[8-10],使目标的角度分辨率得到了提高。由于涡旋电磁波目标回波中带有非线性的贝塞尔函数项,这类方位角估计方法均对回波信号中的贝塞尔函数进行了近似处理,影响了估计精度。
目前对均匀圆阵产生涡旋电磁波的分析大多忽略了阵元间的互耦[11],即假定发射信号不会产生二次辐射。此外,根据奈奎斯特采样定理,均匀圆阵的阵元间隔小于或等于半波长是产生涡旋电磁波的必要条件。当阵列天线工作在毫米波或者更高频段时,天线间的距离较短,将导致阵元间的互耦问题。另外,当天线为共形阵列时[12-13],还将出现阴影效应和平台效应,阵列性能受到严重影响。互耦对阵列的影响表现为导向矢量的失配,大多数高分辨波达方向估计(DOA)估计算法对阵列流形的误差比较敏感,将导致角度估计性能的退化。
互耦导致的误差可以通过互耦矩阵补偿消除。常见的互耦分析方法有开路电压法[14]、全波法[15]、接收互阻抗法[16]和自校正方法[17-18]等。为解决均匀圆阵中的互耦问题,文献[14]基于电路模型,将天线阵元上的激励电压分解为球谐模式[19-20]。文献[16]通过接收互阻抗法得到了与目标俯仰角相关联的互阻抗矩阵。文献[21]结合阵列S参数和接收信号,提出了虚拟阻抗互耦校准方法,该方法与传统互耦补偿矩阵相比具有更小的计算量。
本文利用均匀圆阵互耦矩阵的循环对称性,通过相位模式构造互耦效应的等效电路模型,将阵元间的互耦转化至模式域,分析互耦对涡旋电磁波方位探测的影响,并采用有源单元方向图法进行仿真。此外,本文利用贝塞尔函数的递推关系,提出一种基于OAM的改进传播算子方法,分析一些常用的典型算法在本文信号模型下的估计性能。
1 OAM模型
在无线电目标探测中,涡旋电磁波可以由均匀圆环阵列天线产生。如图1所示,个阵元均匀分布在半径为r的圆周上,数字1、2、n、N表示阵元序号,φ为入射信号的方位角,φn为第n个阵元与第1个阵元的夹角。以圆心为原点建立球坐标系,圆阵位于Oxy面上。为了产生模式数为l的涡旋电磁波,对每个阵元施加相位为lφn=2πl(n-1)/N(n=1,2,…,N)、幅值为I0的激励,相邻两个阵元间的相位为Δφ=2πl/N。空间中与原点距离为R的任意一点P0(R,θ,φ)的电场E(r)可以表示为
(1)
式中:r为P0点的位置矢量;j为恒定电流密度矢量;ω为信号角频率;μ0为真空磁导率;d为偶极子长度;k为波数,k=2π/λ,λ为波长;rn为第个阵元的位置矢量,rn=(Rcosφn,Rsinφn,0)。用|r-rn|≈R和|r-rn|≈R-·rn分别作为远场幅度和相位的近似[6],其中为r的单位向量。
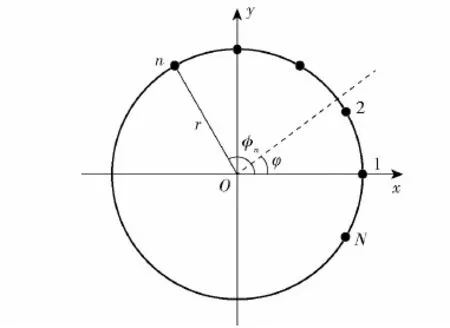
图1 均匀圆阵几何结构Fig.1 UCA array geometry
离散的均匀圆阵可以看作是连续圆阵在每个阵元处馈入激励,即连续圆阵的采样。采样函数s(φ)可以表示为一个周期为2π/N的均匀单位脉冲序列:
(2)
式中:δ(·)表示单位阶跃函数。则归一化电场可表示为
J(l+qN)(krsinθ)ej(l+qN)φ
(3)
式中:Jl为l阶第1类贝塞尔函数。
离散均匀圆阵用于产生涡旋电磁波时,主项由于采样会产生周期延拓,式(3)中的求和项包含无穷多个高阶模式数。在涡旋电磁波应用中只希望产生主模式,而其他周期延拓分量是多余的。根据贝塞尔函数的性质可知,当贝塞尔函数的阶数大于其辐角krsinθ时其幅值Jl(krsinθ)≈0,故模式数l>kr的项可以忽略。另一方面,根据奈奎斯特采样定理,N个阵元的均匀圆阵最多可以产生L=⎣(N-1)/2」个涡旋电磁波模式,⎣·」表示向下取整。因此可以得到kr
2 互耦分析
由第1节的结论可知,用于产生涡旋电磁波的均匀圆阵,其阵元间距小于半波长,且电磁波频率并非是不变常数。当阵列工作在较高频段时,产生涡旋电磁波不仅受空间采样影响,阵元间还存在互耦。
在阵列天线分析中,互耦效应常用阻抗矩阵Z描述。考虑所有阵元之间都存在互耦,即互耦自由度为N,则
(4)
式中:Zmn为第m个和第n个阵元间的互阻抗,
Zmn=Vm/In
(5)
Vm(m=1,…,N)为第m个阵元的开路电压,In(n=1,…,N)为当其他阵元开路、第n个阵元的短路电流。如图3所示,发射信号经相位加权后馈给各个天线,发射阻抗ZG1,…,ZGN可以表示为一个对角矩阵ZG,则互耦矩阵C为
C=(ZG+Z)-1Z
(6)
图3中,Port1、Port2、…、PortN分别为天线的等效端口。将上述互耦模型代入涡旋电磁波信号中,可得
E(θ,φ)=ICa(θ,φ)
(7)
式中:I为第l个OAM模式的激励矢量,
I=I0[ejlφ1,ejlφ2,…,ejlφn]
(8)
a为理想情况下的导向矢量,
(9)
通过以上分析可知,阵列天线的性质可以完全由阻抗矩阵Z和a(θ,φ)表征。
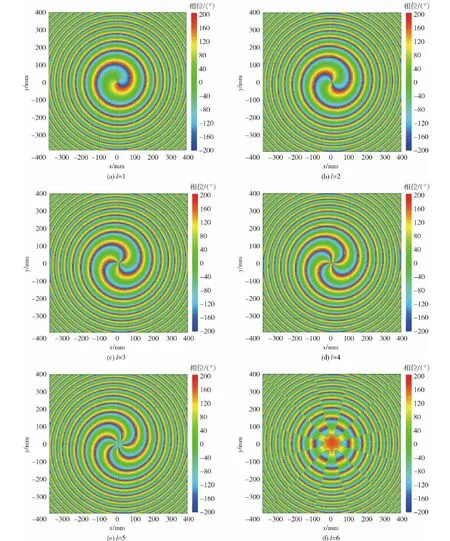
图2 理想情况12阵元不同OAM模式相位分布图Fig.2 Phase distribution of different OAM modes of 12 elements in ideal conditions
对于每一个OAM模式,可以通过对互耦矩阵做离散傅里叶变换,将各个阵元间的互耦分解成相位序列c,其中第l个元素为
(10)
式中:Cmn为第m个和第n个阵元间的互耦。当圆阵中的阵元相同且各向同性时,任意阵元的阻抗都相同,互耦矩阵C具有循环对称性,式(10)可以简化为对互耦矩阵的第1行做离散傅里叶变换(DFT):
(11)
图4将均匀圆阵中的互耦表示成OAM模式,其中等效电流,等效电阻和等效电压分别展开成自变量为l的序列。图4中,Voc为开路电压源,zl为等效负载阻抗。由此可得互耦情况下空间任意一点的归一化电场为
E(θ,φ)=cljlJl(krsinθ)ejlφ
(12)
3 方位估计
3.1 涡旋电磁波接收信号模型
基于多发单收的涡旋电磁波目标探测原理如图5所示。振荡器产生的载频信号经波形调制器调制后,经由功率放大器进行放大,放大后的射频信号经过功分器分为功率相同的N路信号,接着移相器给每路信号附加Δφ=2πl/N的相移,再通过均匀圆阵依次发射[-(2L+1),2L+1]OAM模式数的涡旋电磁波。接收天线位于阵列圆心,回波信号进入混频器与载频信号进行混频得到中频信号,经放大滤波后在OAM域进行采样,最后通过信号处理得到目标方位角信息。
假设空间中存在P个目标,回波信号和噪声均为平稳、零均值、不相关的随机过程。则接收回波信号可以表示为
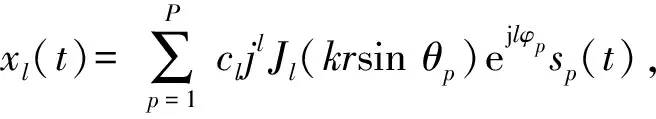
(13)
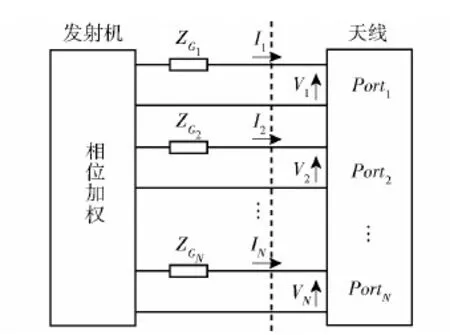
图3 阵列互耦馈电网络图Fig.3 Schematic of the array mutual coupling feeding network
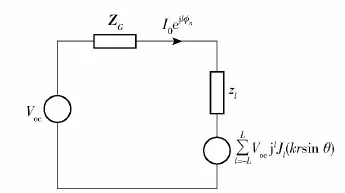
图4 均匀圆阵互耦OAM模式等效电路图Fig.4 OAM mode circuit model of the UCA including mutual coupling

图5 涡旋电磁波探测原理图Fig.5 Schematic diagram of vortex electromagnetic wave detection
式中:sp(t)为第p个空间信号。写成矢量形式为
X(t)=ClBS(t)+N(t)
(14)
式中:Cl=diag(c);B为模式空间流形矩阵,B=[b1,b2,…,bp,…,bP],
bp=jlJl(krsinθp)ejlφp,l={-L,…,0,…,L}T
(15)
S(t)为信号矢量;N(t)为功率为σ2的高斯白噪声。
3.2 MUSIC算法
接收数据的协方差矩阵为
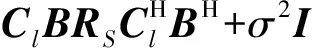
(16)
式中:RS为信号协方差矩阵,RS=E[S(t)SH(t)]。对R进行特征值分解,令US为信号子空间,则谱估计[22]为
(17)
式中:W=diag(jlJl(krsinθ));v(φ)=ejlφ。方位角可以通过对P个谱峰的搜索得到。图6为MUSIC算法的方位角估计谱,其中阵元数N=12,半径r=λ,目标方位角分别为50°和80°。由图6可以看出,阵列互耦对目标方位角估计产生了严重影响,通过互耦校准可明显改善阵列估计性能。
3.3 OAM-PM算法
MUSIC算法需要对协方差矩阵进行特征值分解和谱峰搜索,计算量较大。传播算子算法利用线性运算替代了特征值分解,降低了计算复杂度。现有的传播算子算法在对导向矢量矩阵分块时,通常将非奇异矩阵用导向矢量的前P行来定义[23]。然而在涡旋电磁波探测中,由式(13)可知不同模式数的回波信号幅值受贝塞尔函数调制,模式数较低时对应的幅值较大。因此本文为了提高方位估计的稳健性,对传播算子矩阵进行了重新定义,提出一种基于OAM的传播算子方位估计方法。
将矩阵B分块:
(18)
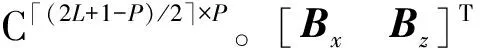
(19)
式中:P为传播算子矩阵,P∈CP×(2L+1-P)。定义矩阵:
(20)
式中:P1为P的前⎣(2L+1-P)/2」列;P2为P的后「(2L+1-P)/2⎤列。由式(19)和式(20)可得
QBy=B
(21)
矩阵Q∈C(2L+1)×P张成的空间与矩阵B张成的模式空间是同一个空间。
在噪声和互耦情况下,P可以从接收信号中得到。计算协方差矩阵
(22)
式中:t为时间变量;K为快拍数。将分块
(23)
式中:R1∈C(2L+1)×⎣(2L+1-P)/2」;R2∈C(2L+1)×P;R3∈C(2L+1)×「(2L+1-P)/2⎤。根据式(18)和式(19)可得
(24)
通过最小二乘法可以得到P的估计:
(25)
由于传播矩阵中含有贝塞尔函数,可以利用式(26)的递推关系[24]:
(2l/krsinθ)Jl(krsinθ)=Jl-1(krsinθ)+Jl+1(krsinθ)
(26)
取Q和B的前2L-1行、第2~2L行和后2L-1行,分别定义为Q1、Q2、Q3和B1、B2、B3。将分块矩阵分别代入式(21),可得
Q1Bx=B1,Q2Bx=B2,Q3Bx=B3
(27)
根据贝塞尔函数的性质可得B1、B2、B3具有如下关系:
DB2=B1Φ+B3Φ*
(28)
式中:D=(2/krsinθ)diag{-(L-1),…,0,…,(L-1)};Φ=diag(ej(φ1+π/2),ej(φ2+π/2),…,ej(φP+π/2));Φ*为Φ的共轭转置。同理可得
DQ2=Q1Ψ+Q3Ψ*
(29)
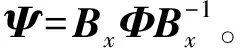
(30)
可得
(31)
式中:†表示Moore-Penrose伪逆;Ψ*为Ψ的共轭转置。对Ψ特征值分解即可获得目标的方位角:
φp=arg (λp)-π/2
(32)
经过以上分析,本文所提解耦合OAM方位估计算法步骤如下:
2) 将协方差矩阵分块,由式(25)得到传播算子矩阵P,并通过式(20)得到矩阵Q。
3) 将矩阵Q划分为Q1、Q2、Q3,分别为Q的前2L-1行、第2~2L行和后2L-1行。
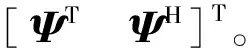

4 仿真分析
4.1 阵列互耦仿真
互耦矩阵通过有源单元方向图法得到[25]。天线的有源单元方向图是指阵列中只激励一个单元,同时其他所有单元终端都接匹配负载时的辐射方向图。当阵列天线单元间存在互耦时,阵列环境中的单元辐射方向图与孤立单元方向图不同。有源单元方向图法是将孤立单元方向图和有源单元方向图通过互耦矩阵建立联系:
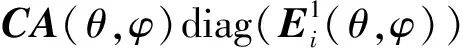
(33)

通过最小二乘法求解互耦矩阵:
(34)
阵列参数由表1所示。

表1 FEKO仿真参数Table 1 FEKO simulation parameters
通过FEKO仿真得到耦合相位序列为
c=[0.743 1+0.229 0i,0.980 4- 0.041 3i,0.894 1-0.082 5i 1.242 8+0.120 0i,1.280 1-0.261 7i, 1.245 7+0.121 3i 1.280 1-0.261 7i,1.242 8+0.120 0i, 0.894 1-0.082 5i 0.980 4-0.041 3i,0.743 1+0.229 0i]
(35)
4.2 计算复杂度
本文算法涉及协方差矩阵计算、矩阵特征值分解、矩阵伪逆和最小二乘法等运算。假设快拍数为K,谱峰搜索范围为[0°,360°),谱峰搜索步长为1°,各算法计算复杂度如表2所示。

表2 不同算法的计算复杂度Table 2 Computational complexity of different algorithms
图7为快拍数K=100、最大模式数L变化范围为5~100时算法计算出的复杂度曲线。
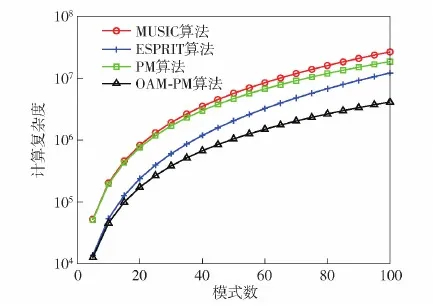
图7 不同模式数的计算复杂度Fig.7 Computational complexity of different mode numbers
图8为模式数L=50、快拍数K变化范围为50~1 000时算法计算出的复杂度曲线。
从图7和图8中可以看出,本文算法将MUSIC算法和ESPRIT算法中2L+1维的矩阵特征值分解改进为求P维矩阵的Moore-Penrose逆,同时还避免了谱峰搜索,降低了计算复杂度。
4.3 性能分析
为验证所提算法在不同阵列配置下的方位探测性能,在阵元数N=12、半径r=λ的均匀圆阵上进行了200次独立的蒙特卡洛仿真。其他仿真参数设置如下:载频f=24 GHz,总模式数2L+1=11,目标个数P=2,方位角分别为30°和80°。
无条件信号模型的克拉美罗界[26]可以表示为

(36)

定义均方根误差为
(37)
图9为快拍数为1 000、信噪比变化范围为0~30 dB时,不同算法计算出的均方根误差随信噪比变化的曲线。
图10为信噪比为10 dB、快拍数变化范围为50~1 000时,不同算法均方根误差随快拍数变化的曲线。

图10 均方根误差与快拍数关系图Fig.10 Dependence of root mean square error on snapshots
由图10可以看出,本文所提算法相较于传统传播算子算法估计误差明显降低,性能与MUSIC算法和ESPRIT算法近似,且具备更低的计算复杂度。
5 结论
本文提出一种解耦合的OAM目标方位探测新算法。首先建立OAM互耦模型,使用FEKO软件对12阵元的均匀圆环阵列偶极子天线仿真得到互耦矩阵,然后通过DFT将其转化到模式域,最后通过OAM-PM算法进行目标方位估计。实验结果表明,所提算法具有良好的解耦合性能,对目标方位角具备精确探测能力的同时拥有更低的计算复杂度。
