舰船发电系统多状态可靠性马尔可夫报酬模型

陈童, 胡斌, 狄鹏

(海军工程大学 管理工程与装备经济系, 湖北 武汉 430033)

0 引言

为有效满足舰船在不同任务阶段的平稳用电需求,发电系统通常采用冷储备或温储备冗余结构提升系统可靠性。因此,舰用发电系统一般包含多台相同或不同型号的发电机组,而每台机组随着使用时间、强度和外部环境的变化会出现性能的逐步退化。这就要求发电系统必须根据用电需求和在网机组实际性能状态,不断调整并网机组数量,合理分配单机负荷,才能保证整个系统实时响应全舰用电需求变化,保持输出功率稳定。这样,整个发电系统随着单机组性能状态和并网机组数量的变化,会表现出多个不同的功率输出水平,即多种性能状态。

在分析这类具有多种性能状态的装备可靠性规律时,如果将整个系统的状态简单分为运行和故障两大类,则会出现发电系统虽然不能满功率运行,但仍可以有效满足各种任务用电需求的情况,这就说明两状态可靠性模型难以准确反映舰船发电系统的实际可靠性规律[1]。因此,多状态系统可靠性理论被用于分析这类装备可靠性问题[2-4],如在各种冗余结构的复杂系统[5-6]、供应链网络[7]、转动部件[8-9]、电力系统[10-11]等诸多领域。

许多学者利用解析或仿真建模方法对发电系统中的多状态系统可靠性问题展开了研究。如文献[12]采用多状态决策图方法研究了温储备条件下的多状态发电机组和负载分配设备组成的电力系统可靠性问题。Lisnianski等[13]利用Lz变换方法研究了由多个发电机组组成的多状态发电系统短期可靠性问题。Kim等[14]采用统计分析方法研究了在轨航天器发电系统的多状态失效问题。Liu等[15]研究了配电系统中柔性多状态开关可靠性评估的蒙特卡洛仿真方法。这些研究表明电力系统的可靠性分析和评估工作必须考虑冗余结构类型、设备使用方式、维修策略等诸多因素对系统效能的影响,存在建模分析难度大,模型重用性差等问题。

因此,马尔可夫报酬模型被引入到多状态系统可靠性解析建模工作中。通过对系统性能状态转移过程赋予多样的报酬矩阵,有效拓展了马尔可夫随机建模方法在复杂装备系统可靠性分析工作中的应用,提升了建模灵活性,也降低了解析建模难度[16]。如Dhople等[17]利用马尔可夫报酬模型研究了随机混合系统的可靠性建模问题。Temraz[18]采用模糊非齐次马尔可夫报酬模型对具有多种失效模式的并联退化系统的可靠性问题进行了研究。文献[19]利用马尔可夫报酬模型研究了系统可靠性——费用优化设计方法。刘宇[20]提出了模糊马尔可夫报酬模型用来评估模糊多状态元件的累积性能。

此外,在分析舰船装备可靠性问题时,不能忽视舰船在整个寿命周期内设计有多次计划维修活动的特点。通过合理安排计划维修和日常故障维修内容,可以确保发电系统这类主要装备在计划维修间隔期内能够保持令人满意的可靠性水平。因此,在舰船系统可靠性设计、设备选型、维修方案设计等工作中,可以通过规定系统可用度、停机次数、工作时间等指标约束,从而明确系统平均故障间隔时间、平均修复时间、规定时间内无故障概率等相关参数,体现了可靠性设计对维修性、保障性设计工作的牵引作用。

综上,本文根据舰船发电系统实际使用特点,分析了系统在冷储备条件下的多性能水平特征,考虑舰船计划维修间隔时间设置对系统可靠性参数的影响,采用马尔可夫报酬模型构建了系统状态转移矩阵、报酬矩阵、报酬函数和系统需求满足函数,通过对报酬矩阵元素的合理赋值,获得了系统区间可用度、平均可工作时间、平均停机时间、平均故障次数、计划维修间隔期内的系统可靠度等可靠性参数,并通过算例验证了模型的有效性和适用性。

1 舰船发电系统描述与模型假设

舰船发电系统通常由若干台主发电机组和备用机组组成。主发电机组一般选用同型装备,而备用机组可以选用与主发电机组相同或不同型号。

当全船处于低负荷需求时,只需运行部分主发电机组,其余主机组和备用机组则处于备份状态;当处于高负荷需求时,所有主机组均投入运行,此时只有备用机组处于备份状态。

工作机组由于发生故障或性能下降而无法正常工作时,需要停机进行维修,此时备份机组被迅速启用。

本文以常见的舰船发电系统为例。该系统包含2台主发电机组和2台备用机组。整个系统在低负荷时通常只需1台机组正常工作,在高负荷时2台机组即可满足全船用电需求。可以进一步做出以下假设:

1)主发电机组和备用机组在运行时的故障时间服从指数分布,故障率分别为λM和λS;未运行机组处于冷储备状态,故障率忽略不计;

2)当运行机组出现故障后,备份机组转换运行状态,转换时间忽略不计;故障机组立刻接受维修;

3)主机组和备用机组的修复时间服从指数分布,修复率分别为μM、μS;

4)每个工作周期T内,全船高负荷需求P平均时长为TP,则低负荷需求L平均时长为TL=T-TP。

2 模型状态分析

随着发电系统内各机组实际状态的变化,整个系统的性能是由完好机组数量决定的,因此性能状态集可以表示为G(t)={0,1,2,3,4},其中:水平0表示系统内所有机组均故障;水平1表示系统内只有1台完好机组,发电系统仅能满足需求L;水平2、3、4表示系统中至少有2台机组(包括主机组和备用机组)完好,可以满足需求P。

2.1 系统状态空间划分

系统状态可以分为18个,如图1所示。其中,状态1～状态9对应电力高负荷需求,状态10～状态18对应电力低负荷需求。图1中,γPL和γLP分别为高负荷向低负荷需求和低负荷向高负荷需求转换时系统状态的转换率。

当系统处于状态1和状态10时,系统内2台主机组和2台备用机组均处于完好状态,此时的系统性能水平为G1(t)=G10(t)=4。

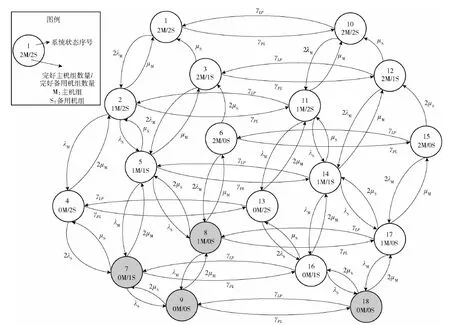
图1 舰船发电系统状态转移图Fig.1 State-transitions diagram of ship power generation system

当系统处于状态2和状态11时,系统内1台主机组和2台备用机组处于完好状态,此时系统性能水平为G2(t)=G11(t)=3。

当系统处于状态3和状态12时,系统内2台主机组和1台备用机组处于完好状态,此时系统性能水平为G3(t)=G12(t)=3。

当系统处于状态4和状态13时,系统内只有 2台备用机组处于完好状态,此时系统性能水平为G4(t)=G13(t)=2。

当系统处于状态5和状态14时,系统内1台主机组和1台备用机组处于完好状态,此时系统性能水平为G5(t)=G14(t)=2。当系统处于状态6和15时,系统内只有2台主机组处于完好状态,此时系统性能水平为G6(t)=G15(t)=2。

当系统处于状态7和状态16时,系统内只有 1台备用机组处于完好状态,此时系统性能水平为G7(t)=G16(t)=1。

当系统处于状态8和状态17时,系统内只有 1台主机组处于完好状态,此时系统性能水平为G8(t)=G17(t)=1。

当系统处于状态9和状态18时,系统内所有机组均处于故障状态,此时系统性能水平为G9(t)=G18(t)=0。

由此可知,在状态7、状态8、状态9、状态18时,发电系统性能是无法满足全船电力需求的,此时可以认为系统处于故障状态(图1中标注为灰色),而其余状态可以认为是系统的运行状态。因此可以将系统状态划分为运行状态集ΩO∈{1,…,6,10,…,17}和故障状态集ΩF∈{7,8,9,18}。

2.2 系统状态的转换

图1中的系统状态转换可以分为如下3类:

1)从所有机组完好(状态1、10)逐步向全部故障(状态9、18)的转换。这类转换中只需考虑正在运行的机组的失效率。如状态2向状态5的转换,说明此时只有1台备用机组在运行,因此状态转换率就为该备用机组的失效率λS。

2)从全部故障(状态9、18)逐步向所有机组完好(状态1、10)的转换。根据假设条件知故障机组均及时得到维修,因此转换率取决于故障机组的数量。如状态7向状态5的转换率是两台主机组的修复率,即2μM。

3)高负荷与低负荷需求的相互转换。当用电需求发生变化时,就产生了高负荷与低负荷需求之间的相互转换,系统状态(如状态1和状态10的转换)的相互转换率分别为γPL=1/TP、γLP=1/TL。

2.3 系统状态转移矩阵

根据马尔可夫转移过程,系统的状态转移矩阵[2]可以表示为

(1)

式中:QPP表示高负荷需求时的状态转换;QLL表示低负荷需求时的状态转换;QPL表示高负荷向低负荷变化时的状态转换;QPP表示高负荷需求情况的状态转换。因此有

QPP=

QLL=

式中:C1=2λM+γPL;C2=λM+λS+μM+γPL;C3=2λM+μS+γPL;C4=2λS+2μM+γPL;C5=λM+λS+μM+μS+γPL;C6=2λM+2μS+γPL;C7=λS+2μM+μM+γPL;C8=λM+μM+2μS+γPL;C9=2μM+2μS+γPL;C10=2λM+γLP;C11=λM+λS+μM+γLP;C12=2λM+μS+γLP;C13=2λS+2μM+γLP;C14=λM+λS+μM+μS+γLP;C15=2λM+2μS+γLP;C16=λS+2μM+μS+γLP;C17=λM+μM+2μS+γLP;C18=2μM+2μS+γLP。

3 系统马尔可夫报酬模型

在构造发电系统的马尔可夫报酬矩阵和效能需求函数后,通过改变系统报酬矩阵的赋值,可以方便地获得该系统的各可靠性参数。

3.1 系统马尔可夫报酬矩阵的构造

针对2.3节构造的连续时间马尔可夫过程,其状态集可以表示为S={1,…,K},本文中K=18。

将式(1)的系统状态转移矩阵写为Q=[qij],i,j=1,…,K,qij表示从状态i到状态j的转移率。

假设系统停留在状态i的每个单位时间的报酬为rii,系统每次从状态i到状态j的报酬为rij。这里的报酬表示消耗或增收了包括费用在内的各类资源。因此当报酬取负值时表示资源的消耗,报酬取正值时则表示资源的增收,则可以构造出如式(2)报酬矩阵[18]:

R=[rij]

(2)

因此,过程{Q(t),R(t)}就是一个考虑报酬的马尔可夫过程[21]。

3.2 系统报酬函数

如果系统在初始时刻t=0 h处于状态i,令Vi(t)表示在时刻t时的平均总报酬。

系统经过时长Δt后,有两种可能的状态:

1)仍处于状态i。此时有Vi(Δt)=riiΔt。

若在随后的区间[0 h,Δt+t],系统仍停留在状态i,则有

Vi(Δt+t)=riiΔt+Vi(t)

(3)

可知系统在时长Δt停留在状态i的概率为

(4)

2)转入了状态j。可知有πij(0,Δt)=qijΔt,此时Vi(Δt)=rij。而在区间[Δt,Δt+t],系统将从状态j开始向其他状态转移,在时长t的平均总报酬则为Vj(t)。因此,在[0,Δt+t]区间有

Vi(Δt+t)=rij+Vj(t)

(5)

根据式(3)～式(5)可知:若Δt→0,则有

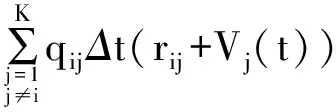
(6)

将式(6)表示为极限形式,有

(7)

同时,在时刻t=0 h,有如下边界条件:

Vi(0)=0

(8)

利用Laplace-Stieltjes变换可以对方程组式(7)、式(8)求解。

3.3 系统需求满足函数

在分析图1的系统状态转移过程时,可以发现全船的电力需求量变化过程D(t)和发电系统性能水平变化过程G(t)一样,都是马尔可夫链。D(t)的状态转移矩阵可以表示为

(9)

显然,G(t)和D(t)两个随机过程相互独立,可以构建系统需求满足函数,形式为

S(G(t),D(t))=G(t)-D(t)

(10)

因此,只有在S(G(t),D(t))≥0时,发电系统才处于能够满足全船用电需求的状态。

3.4 系统可靠性参数

令系统在t=0 h时刻的初始状态为i,可以分别给出如下系统可靠性参数:

1)系统区间可用度Ai(t)。根据区间可用度[22]的概念,可以令Ai(t)表示系统在[0 h,t]内能够满足用电需求的平均时间与时长t的比值。因此,可以按照如下规则定义报酬矩阵中的元素rij:

系统停留在状态l(l=1,…,K)时,若S(G(t),D(t))≥0,则rll=1;若S(G(t),D(t))<0,则rll=0;系统状态之间转换时的报酬均为0。

此时报酬函数Vi(t)表示的就是初始状态为i时,发电系统在[0 h,t]停留在可接受状态的平均总时长。因此有

(11)

2)系统平均可工作时间MOTi(t)。计算MOTi(t)时,只需计算系统在[0 h,t]停留在运行状态集ΩO的时间。因此可以参照计算Ai(t)构造报酬矩阵中的元素rij,此时有

MOTi(t)=Vi(t)

(12)

3)系统平均停机时间MDTi(t)。系统平均停机时间就是系统无法满足全船用电需求的平均时间,即系统处于故障状态集ΩF的平均时间。因此,可以按照如下规则定义报酬矩阵中的元素rij:

系统停留在状态l(l=1,…,K)时,若S(G(t),D(t))≥0,则rll=0;若S(G(t),D(t))<0,则rll=1;系统状态之间转换时的报酬均为0。

此时报酬函数Vi(t)表示的就是初始状态为i时,发电系统在[0,t]停留在故障状态的平均总时长,因此有

MDTi(t)=Vi(t)

(13)

4)系统平均故障次数Ni(t)。Ni(t)为系统在[0 h,t]进入故障状态的平均次数。因此,可以按照如下规则定义报酬矩阵中的元素rij:

每次系统从运行状态集ΩO向故障状态集ΩF转移时,有rij=1,其余rij均为0。

因此有

Ni(t)=Vi(t)

(14)

对报酬矩阵中的元素rij进行定义:

系统从ΩO向ΩF转移过程的报酬rij=1,其余rij均为0。

此时报酬函数Vi(t)表示初始状态为i时,整个发电系统在t时刻进入故障状态的概率,因此有

Rei(t)=1-Vi(t)

(15)

4 算例分析

根据对舰船发电系统使用数据的统计分析,可以令:λM=15次/a,λS=5次/a;μM=μS=150次/a;TP=2 555 h/a,TL=6 205 h/a。

本算例以完好状态1作为系统初始状态,根据3.4节结论分别构建报酬矩阵R,代入方程组式(7),利用数学分析软件求解微分方程,可以方便地得出系统各个可靠性参数:

1)系统区间可用度Ai(t)。在给定上述发电机组单机故障率、修复率等参数的情况下,可以非常方便的计算出整个发电系统在一段时间的区间可用度Ai(t)。图2显示了在一个舰船计划维修间隔期(3a)内Ai(t)随系统工作时间的变化情况。由图2可以看出,系统区间可用度在整个计划维修间隔期内,均维持在一个较高水平上。

图2 系统工作时间t与系统区间可用度Ai(t)的关系Fig.2 Relationship between the system online time t and the system interval availability Ai(t)

在装备结构设计或设备选型等工作中,可以先给定系统在整个计划维修间隔期的可用度指标约束,然后利用本模型确定发电机组单机故障率、平均修复时间等指标,从而满足整个发电系统的可靠性设计要求。图3就展示了在一个计划维修间隔期内,发电机组单机平均修复时间与整个系统区间可用度指标的关系。例如要确保系统在计划维修间隔期的可用度维持在0.997以上时,必须要求单机组平均修复时间大致不能超出4.5 d,这就对装备维修能力提出了明确约束。

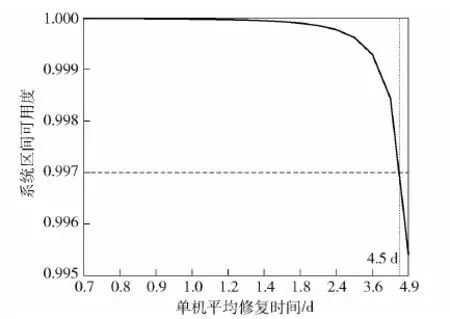
图3 单机组平均修复时间对系统区间可用度 Ai(t)的影响Fig.3 Influence of mean time to repair of single unit on the system interval availability Ai(t)

2)系统平均可工作时间MOTi(t)和系统平均停机时间MDTi(t)。图4、图5分别展示了在一个舰船计划维修间隔期内系统的平均可工作时间和停机时间,可以看出在当前的故障率及修复率条件下,MOTi(t)和MDTi(t)与系统工作时间呈近似线性关系,且MDTi(t)相对整个计划维修间隔期是非常小的(在3a的工作时间内,系统平均停机时间在3.5 h左右),说明发电系统在整个计划维修间隔期内是可以有效满足全船用电需求。

图4 系统工作时间t与系统平均可工作 时间MOTi(t)的关系Fig.4 Relationship between system online time t and mean operational time MOTi(t)

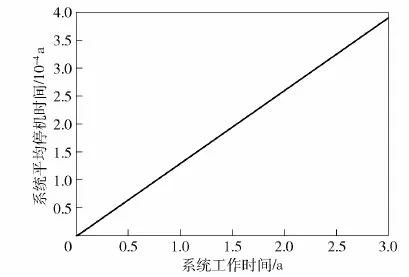
图5 系统工作时间t与系统平均停机时间 MDTi(t)的关系Fig.5 Relationship between system online time t and mean down time MDTi(t)

3)系统平均故障次数Ni(t)。图6展示了在一个计划维修间隔期内发电系统的平均故障情况。可以发现Ni(t)与系统工作时间呈近似线性关系,且整个发电系统在3a内出现崩溃的可能性比较小,这一点与图5显示的情况吻合。

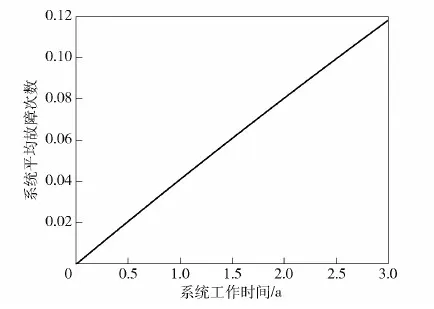
图6 系统工作时间t与系统平均故障次数Ni(t)的关系Fig.6 Relationship between system online time t and mean number of system failures Ni(t)

4)计划维修间隔期内的系统可靠度Rei(t)。图7显示当μM=μS=150次/a时,单机组平均修复时间在2.4 d左右,此时Rei(t)在计划维修间隔期末段(第2a～第3a)的可靠度在0.8附近,处于一个偏低水平,会对全船的正常使用带来明显影响。

图7 系统工作时间t与系统可靠度Rei(t)的关系 (μM=μS=150次/a)Fig.7 Relationship between the system online time t and system reliability Rei(t) (μM=μS=150 times per year)

为了确保系统在整个计划维修间隔期的可靠度水平,提升维修效率是一个非常直接的办法。因此,当单机组修复率μM和μS均提升至500次/a,即单机组平均修复时间降到了0.7 d左右时,在整个计划维修间隔期内的Rei(t)均处在一个较高水平,如图8所示。

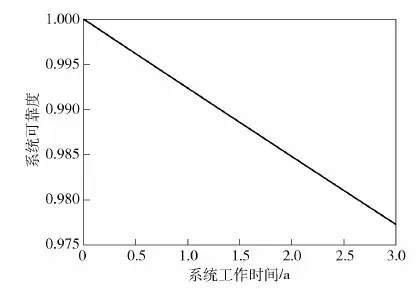
图8 系统工作时间t与系统可靠度Rei(t)的关系 (μM=μS=500次/a)Fig.8 Relationship between system online time t and system reliability Rei(t) (μM=μS=500 times per year)

图9显示了若将计划维修间隔期缩短为1 a时,单机组平均修复时间(或单机组修复率)对系统可靠度的影响。由图9可以看出,为了确保发电系统能够在整个计划维修间隔期维持在设计指标(如0.95)以上,单机组平均修复时间必须限制在2.0 d以内。图10则显示了计划维修间隔期为3a时,单机组平均修复时间对系统可靠度的影响。此时,只有将单机组平均修复时间限制在1.15 d以内时,才能有效保证整个发电系统可靠度维持在0.95以上。

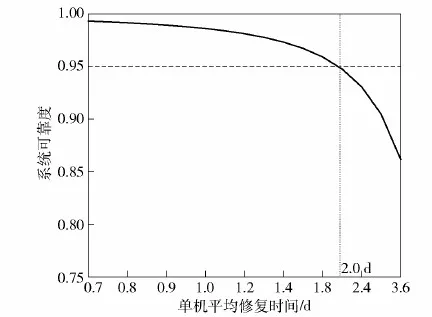
图9 单机组平均修复时间对系统可靠度Rei(1)的影响Fig.9 The influence of mean time to repair of single unit on the system reliability Rei(1)

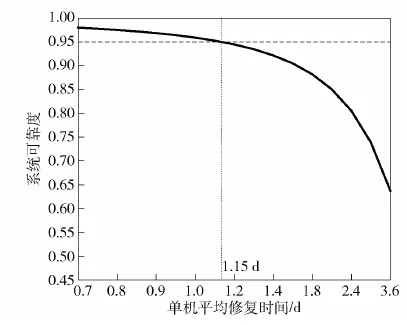
图10 单机组平均修复时间对系统可靠度Rei(3)的影响Fig.10 Influence of mean time to repair of single unit on the system reliability Rei(3)

由图9、图10的对比说明:在给定系统可靠度指标约束后,缩短计划维修间隔期可以降低对单机组平均修复时间的要求,这样就可以适当减少日常维修资源的投入,这与舰船装备使用维护的直观经验是吻合的。但也必须认识到这样做同时会造成计划修理资源消耗的增加。因此需要对舰船计划修理和日常故障修理两类维修活动科学统筹、合理分配,才能在确保系统可靠性指标的同时,充分发挥维修资源效能。

通过上述建模过程和算例可以发现,利用马尔可夫报酬模型进行舰船发电系统多状态可靠性建模时,能够通过对报酬矩阵R中元素rij的灵活赋值,方便高效地得到了多种系统可靠性参数的解析表达式,建模过程标准,模型重用性强,为分析发电系统计划维修间隔期设置对系统可靠性变化规律的影响提供了建模工具,为合理安排舰船装备维修结构提供了技术支持,显然为舰船装备可靠性设计等工作带来了极大便利。

5 结论

本文针对舰船发电系统使用与维修工作特点,利用马尔可夫报酬模型研究了冷储备结构的多状态系统可靠性规律,在保证良好解析特性的同时,通过设计灵活的报酬矩阵,方便地得出了系统区间可用度等可靠性参数,并通过算例讨论了计划维修间隔时间和单机组平均修复时间等指标对系统可靠性的影响。研究过程显示出马尔可夫报酬模型在复杂多状态系统可靠性建模和计算方面的便捷性和灵活性。因此,在今后的研究工作中,可以尝试采用类似研究思路分析复杂系统多状态可靠性建模问题。