整体解读梳理，构建过程探究

王成

［摘  要］ 函数的单调性作为函数部分的重要内容，教学中需要整体解读，分模块引导. 从情境中引入，让学生充分感知；使学生亲历探究过程，体验概念生成；在实例探究中锻炼学生的思维，提升学生的能力. 文章结合课堂实践，开展“函数单调性”的教学探讨.

［关键词］ 函数；单调性；概念；整体化

函数的单调性是高中数学的重要内容，是函数概念的延续和拓展，对后续研究指数函数、对数函数、三角函数等模型有着重要作用. 函数的单调性是学生首次系统研究的函数性质，教学中需要引导学生完成概念的抽象概括，让学生经历完整的探究过程，掌握函数性质的研究方法. 下面开展教学探讨，提出相应的教学建议.

内容整体化分析，梳理教学过程

知识间相互联系，具有一定的整体性和连续性，函数的单调性也不例外. 在教学初始的内容解读中，需要从整体视角来全面分析，包括知识整合、目标设定、活动设计等. 既要突出知识的系统性、教学的指向性，还应赋予知识整体关联性.

1. 内容分析

对于“函数的单调性”的教学，从教材内容来看，教学中需要重视两大层面：一是知识层面，即章节内容的本身；二是思想方法层面，即函数的单调性中所融合的数学思想方法，以及知识探究中需要用到的思想方法.

（1）知识层面的分析. 函数的单调性的探究需要分为两个阶段：阶段一，利用运算的性质来研究函数的单调性，关注函数的变化趋势；阶段二，利用导数知识来研究函数的单调性，需要重点探究函数变化的快慢. 本课的知识探究处于阶段一，教学时要引导学生关注探究核心，明晰探究阶段，让概念自然生成.

（2）思想方法层面的分析. 函数的单调性的教学可视为数学概念教学，也可视为关于数学思想方法的指导教学，探究过程充分体现出研究函数性质的思想方法. 教学过程需要借助图象让学生直观感知并从中抽象概括定义，使学生经历从图形语言到文字语言再到数学符合语言描述概念的思维过程. 同时，在整个探究阶段中充分渗透数形结合思想，在数形结合思想的指导下组织活动.

2. 教学梳理

学生在初中阶段已经掌握了一次函数和二次函数的相关知识，熟知对应图象的几何特征. 学生欠缺的是思维能力和探究经验，尤其是抽象水平，难以理解函数单调性的形式和定义. 因此教学中需要注重几何直观讲解，数形结合辅助分析. 实际教学可按如下思路开展，突破难点.

（1）创设情境.分析与生活实际结合紧密的函数图象，让学生直观感知函数的单调性，合理使用数学符号描述函数变化规律.

（2）引导探究. 引导学生深入学习，通过递进式设问，让学生体验探究过程，实现函数单调性从“直观感知”上升到“严谨论述”.

（3）巩固和强化所学知识. 利用具有代表性的实例，引导学生形成正确的解析思维，提升学生的综合能力.

创设情境，为性质探究做铺垫

建议教师从生活实际中提取素材，引导学生分析直观模型，掌握模型构建与分析的方法. 同时，设问引导需要立足学情，把握学生的知识经验，在此基础上开展观察、猜想、归纳等活動.

1. 情境创设

教学中可创设如下情境：

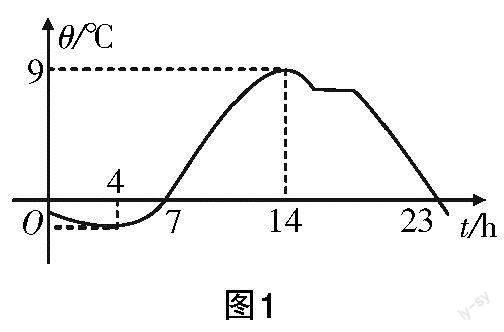
图1是某地1月某天里的气温变化图，请同学们观察气温变化曲线，回答下列问题.

（1）图1中的θ表示气温，t表示时间，如何表述θ随t的变化情况？

（2）在t∈［4，14］上，θ随t的增大而增大，如何使用数学语言来表述？

（3）是否可以表述为“当t=5，t=6，t=8，t=10时，对应的θ，θ，θ，θ满足θ<θ<θ<θ，因此在t∈［4，14］上，θ随t的增大而增大”？

2. 观察探究

在情境设问的基础上，给出如下众多函数图象，进一步引导学生探究.

（1）确定上述图象所对应的函数类型，分别表示什么函数.

（2）这些函数有怎样的变化趋势，如何表述？

上述“情境创设”和“观察探究”两个环节，先引导学生发现生活中的函数，分析函数变化规律；然后从现实生活过渡到数学问题，规范表达函数的单调性，即函数在某区间上具有怎样的变化情况——要强调其中的“某区间”，使学生明白函数的单调性是相对“某区间”而言，具有一定的局限性，为后续“函数的单调性”概念的构建做铺垫.

体验探究过程，概念自然生成

函数的单调性是函数部分的重点内容，教学中需要教师利用直观的函数图象，引领学生由形思数，思维由具象到抽象，引导学生体验函数单调性的探究过程.

1. 直观探索，共性分析

图3是一组三个函数的图象，请指出这三个函数具有哪些共同点.

引导学生从三个函数图象的变化趋势来看——结合x值的变化来分析y值的变化，促使学生深入认识增函数. 在此基础上给出第二组三个函数的图象（见图4），让学生再观察它们的共同点，促使学生深入认识减函数.

2. 数学描述，符号分析

由图象来判断函数的单调性较为直观，不具有准确性，故教学中需要教师合理预设问题引导学生用数学语言来表述函数的单调性，从而生成概念.

（1）辨析.

问题1 已知某函数在区间（0，+∞）上，当x=1时，y=2；当x=2时，y=3.是否可以说明该函数在区间（0，+∞）上，y随x的增大而增大？

问题2 有n个正数x，x，x，…，x，且x<x<x…<x，它们对应的函数值y，y，y，…，y满足y<y<y…<y，是否可以说明在区间（0，+∞）上，y随x的增大而增大？

教学中引导学生举反例来辨析问题1和问题2，让学生不仅关注函数的定义域，而且理解有限点所反馈的增减变化有局限性.

（2）符号化.

教学中引导学生用数学语言来描述函数的单调性，设问如下：若某函数为增函数，是否可以用数学语言来描述？如何用准确的数学语言来表达？请大家小组讨论，交流总结.

教学中引导学生从关键词入手，可分如下四步进行探究.

第一步，“增大”符号化，即当x<x时，y<y；

第二步，“随着”符号化，即当x<x时，f（x）<f（x）；

第三步，“任意”符号化，引导学生联想前面讨论的内容，跳出单一数值对单调性描述的局限，明白：对于任意的x<x，均有f（x）<f（x）；

第四步，“区间”符号化，引导学生关注变量x和x的取值范围，明确函数的单调性与区间紧密相关，即强调x，x∈I（I为函数的单调区间）.

（3）生成概念.

完成上述四步探究后，引导学生将其串联起来，从而生成完整的单调递增的概念. 教学中可以借助直观的函数图象，采用数形结合的方式概括单调性概念.

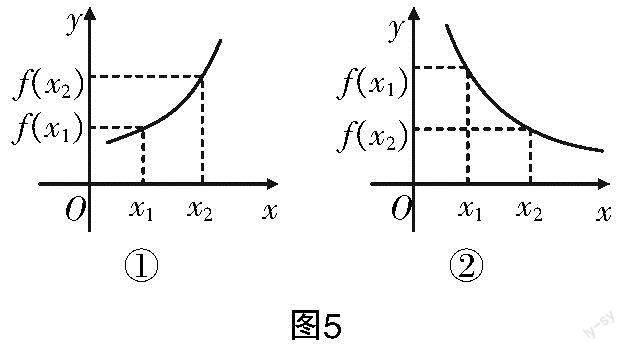
单调递增：对于区间I内的任意两个值x，x，当x<x时，均有f（x）<f（x），如图5①.

单调递减：对于区间I内的任意两个值x，x，当x<x时，均有f（x）>f（x），如图5②.

函数单调性的概念可按照上述三个环节来构建，简而言之，即先引导学生观察函数图象，然后让学生猜想并加以辨析论证，在此基础上引导学生明晰概念符号化，生成完整的单调性概念.

实例引入，概念强化

“函数的单调性”的教学，要经历概念生成和应用强化两个阶段，故概念生成后，有必要引入实例，帮助学生巩固和强化所学知识. 值得注意的是，实例要围绕函数单调性概念的三个核心内容（变量区间、对应关系、变化）而引入. 通过开展解题引导，帮助学生构建解析思维.

该区间上的单调性.

完成以下证明.

（1）函数f（x）在（0，1）上递减；

（2）函数f（x）在（0，+∞）上递增.

解题引导：让学生立足函数单调性的定义，按照“设元—代入—作差—变形—判断”的步骤完成证明. 同時，引导学生梳理证明过程，让学生明白每一步的思维方法.

总之，教师要深入解读知识内容，围绕教学重点梳理知识模块，基于知识模块开展探究活动，引导学生经历探究过程，使学生认识知识的本质，提升数学思维能力.