数学化：数学核心素养培养的一种重要方式

谢循 严艳华

［摘  要］ 在当下“问题—情境”教学模式的导向下，存在着重横向数学化、轻纵向数学化的教学认知偏差. 然而，数学化是学生的数学学习过程，对发展学生的数学核心素养具有重要意义. 文章从培养学生数学核心素养的视角阐述数学化的具体含义，以一个具体案例——非直线追及问题，揭示数学化的思想价值，并提出几点教学反思：一是数学化与情境化并不相悖，二是数学化不等于形式化，三是均衡的数学化教学是一个寻求过程，旨在更好地指导教学.

［关键词］ 数学化；核心素养；数学教学

数学化是荷兰著名数学家及数学教育家弗赖登塔尔（H.Freudenthal）的著作《作为教育任务的数学》中的一个核心思想. 弗赖登塔尔首次提出“数学化”作为数学教育的三大基本原则之一，并且提出数学教育的目的应该是数学化. 所谓数学化就是用数学方法观察世界、分析研究各种具体现象并加以整理的过程.简言之，“数学化就是数学地组织现实世界的过程”［1］.

核心素养是学生应该具备的适应终身发展和社会发展所必需的关键能力，培养学生的数学核心素养是数学课程目标的核心，也是实现育人价值的重要途径. 《普通高中数学课程标准（2017年版2020年修订）》中关于数学核心素养的提升主要包括“三会”——会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界［2］. 显然，让学生充分经历数学化过程是培养学生核心素养的重要方式.

在新时代的课程理念背景下，《普通高中数学课程标准（2017年版2020年修订）》数次强调要将现实生活作为学生学习数学的一个出发点，无疑，这样的导向对于数学教育来说是合理的，因为以现实情境为开端引发学生的认知冲突，激发学生的学习兴趣，这对学生来说是一种极佳的学习方式. 然而，过多关注情境创设而忽略问题自身的数学意义，会导致数学问题情境化与情境问题数学化这样一个“天平”失衡. 数学化作为学生数学学习的一种重要方式，其意义何在？对此问题进行思考，有助于教师理解数学化思想，更好地看待数学化在核心素养培育中的地位和作用.

数学化思想

数学化是指将现实问题转化为数学语言的过程. 在这方面，弗赖登塔尔接受了特莱弗斯（Treffers）关于数学化的划分——将数学化划分为两种，分别为横向数学化和纵向数学化［3］.

1. 横向数学化，从现实世界走向数学世界

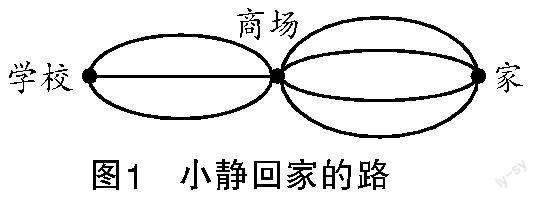
横向数学化是把现实世界引向数学世界的过程，是数学问题解决过程中的重要阶段. 具体来说，就是发现现实世界中存在的数学问题及数学信息，将这些数学问题及数学信息用数学符号表示出来，即把现实问题表述为数学问题的过程. 如这样一个实例：“小静回家的路有几条？”——小静从学校到家要经过一个商场，从学校到商场有三条不同的路可走，从商场到家有四条不同的路可走，那么小静放学回家的路一共有多少条呢？这对学生来说是一个十分生活化的案例. 那么横向数学化在这里是如何体现的呢？首先每一条路用线来表示，其次学校、商场、家分别用点来表示，最后只要数出两点间有多少条线就能解决这个问题，从而自然而然地将这个现实问题抽象成了数学“组合”问题（如图1所示）.

2. 纵向数学化，数学世界中符号的重塑与使用

纵向数学化是指经历横向数学化将现实问题转化为数学问题后，再运用数学的方法进行处理，即将符号化问题进一步抽象以达到一般化. 例如，在横向数学化中，将现实问题“小静回家的路有几条”转化成具有符號特征的数学“组合”问题后，教师先让学生亲自数一数一共有几条路可以到家：首先学校到商场有3条路，其次商场到家有4条路，因此从学校到家就有3×4=12条路. 然后经过一般化可得乘法原理：完成一件事情需要分成n个步骤，做第一步有M种不同方法，做第二步有M种不同方法……做第n步有M种不同方法，那么完成这件事就有M×M×…×M种不同方法.

3. 数学化具体过程

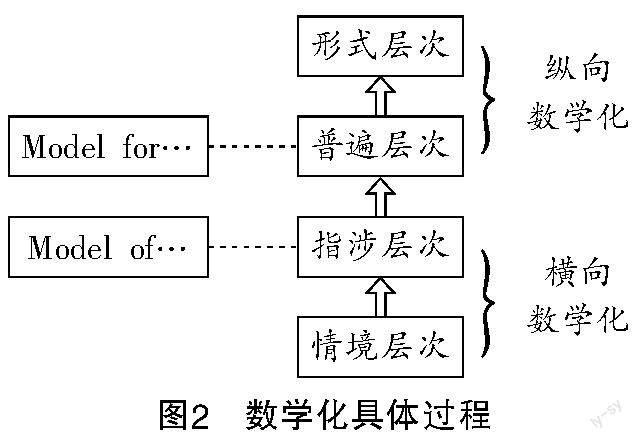
在数学化的过程中，横向数学化与纵向数学化不能随意分开，两者的作用是相互交织、不可分割的. 数学化是一种由浅入深，具有不同层次、不断发展的过程［4］. 一个完整的数学化过程包含四个层次，如图2所示. 横向数学化与纵向数学化体现在这四个层次中.

第一个层次是情境层次（situation level），顾名思义，这个层次与“情境”的关系密切，即现实世界与数学世界的联系.在这个层次中，学生的活动是从问题情境中去思考如何解决问题. 第二个层次是指涉层次（referential level）或者称为“model of”层次，学生在这个层次能够根据实际情境中提出的问题得到一个数学模型，也就是说根据当前的实际背景来构建数学模型. 第三个层次是普遍层次（general level）或者称为“model for”层次，学生在这个层次能够得到含有普遍意义的数学模型，同时将模型策略运用到不同情境中. 最后一个层次是形式层次（formal level），学生在这个层次可以进行纯粹思维、反思及欣赏活动，这是数学对象已经引用在数学范畴内规范化的步骤和符号进行表述和操作的缘故［5］. 前两个层次属于横向数学化，后两个层次则属于纵向数学化. 总的来说，数学化就是从现实世界到数学世界内部，从内部发展，再到现实生活中（以及应用于其他学科）的全过程［6］. 因此，核心素养是学生经历数学化活动后得到的产物.

以均衡的数学化，发展学生的核心素养

下面以一个具体案例展示数学化的四个层次，并且揭示其培养学生数学核心素养能力的价值.

案例 在一个湖岸边（可将湖岸看作直线）停放着一条小船，由于缆绳突然断开，小船被风刮跑，其方向与河岸成15°角，速度为2.5 km/h. 同时岸上有一人从同一地点开始追赶小船，已知他在岸上跑的速度为4 km/h，在湖中游的速度为2 km/h. 问：此人能否追上小船？小船能被追上的最大速度是多少？

1. 通过探究现实情境，学会用数学的眼光观察现实世界

考虑到人在湖中游的速度小于小船被风刮跑的速度，如果人直接跳入湖中去追小船不可能追得上，因此，一种可行的方法是：先在岸上跑一段路后再跳入湖中去追小船. 这样追小船的问题就转化成了求三角形三边关系的问题——人在岸上跑的轨迹、小船被风刮跑的轨迹以及人在湖中游的轨迹可以构成一个三角形. 如图3所示，AB为人在岸上跑的轨迹，AC为小船被风刮跑的轨迹，BC为人在湖中游的轨迹. 如何解决这个三角形问题呢？这成为解决追小船问题的关键. 此时，现实生活问题与数学就有了联系.

在这个情境层次中，学生经过思维活动将已有的生活经验与知识经验结合起来，把一个实际问题转变成了数学问题. 这个过程促使学生用数学的眼光观察现实世界，发展学生的抽象能力以及想象能力；让学生发现数学在现实生活中无处不在，感悟数学的魅力，从而提高学生的数学学习兴趣.

2.经历实际背景下的数学模型的构造，学会用数学的思维思考现实世界，用数学的语言表达现实世界

由于小船在湖中被风刮跑的时间等于人在岸上跑的时间与在湖中游的时间之和，因此得出一个关于三角形的数学模型就是解决问题的关键，并运用所学知识将三角形三边的数量关系表示出来.

如图4所示，假设小船的速度为v（单位：km/h），人追上小船所用的时间为t（单位：h），人在岸上跑的时间为kt（0<k<1），则人在湖中游的时间为（1-k）t. 人要追上小船，就有

要使①式（关于k的方程）在0<k<1内有实数解，则需要满足：

当学生用数学关系式去表示所构造的三角形的三边时，其数学化就进入了指涉层次，学生的思维在几何直观、数学建模以及数学运算的过程中得到挖掘和提升. 首先，可以构造三角形来描述实际问题并且通过三角形三边的数量关系以及已有的知识经验（如余弦定理）来解决问题. 其次，本例运算量较大，学生可以将未知问题与脑中图式转化为原本知识体系中存在的关于一元二次方程的同型问题展开运算，通过运算促进思维的发展. 最后，学生可以在现实情境中用数学的眼光发现问题解决的关键——构造三角形，并用符号语言和图形语言表达所构造的三角形，进而解决问题. 这一过程有助于学生深刻体会现实世界与数学之间的关系，学会用数学模型解决实际问题.

可见，在解决这类非直线追及的问题时，学生的思维进入了数学化的普遍层次，即当两个物体在某一时刻到达同一位置时，不仅需要把握它们的时间关系，而且两个物体不在同一条直线上运动，需要构造几何图形，比如三角形来解决问题.

无疑，在上述的数学化过程中，学生能从具体的情境中发现问题、提出问题以及解决问题. 整个过程贯穿对数学问题的思考、数学方法的运用以及数学思维的重构，促使学生在实际背景下构造数学模型，发展用数学思维思考现实世界的意识和能力. 更重要的是，学会用数学语言表达现实世界，从中感悟数学对于现实生活的重要意义.

3. 在数学活动的反思中，欣赏数学的魅力

反思以上问题的解决过程，通过探讨非直线追及问题的共性，揭示该数学模型的本质——构造三角形及三角形三边的关系，了解数学以及各个学科的知识在现实生活中的应用，由此学生的思维进入了数学化的形式层次. 在此过程中，学生增进了数学与其他学科的联系——通过与物理知识的融合，形成跨学科的应用意识与实践意识，感悟数学知识的共性通性以及魅力.

进一步的反思

1. 数学化与情境化并不相悖

重横向数学化、轻纵向数学化的教学认知偏差即教师在教学过程中过于注重情境——为了联系生活而创设一些无关数学本质的情境，教师通常以这样的方式来形式化地完成课堂教学. 然而，数学化中强调“情境”是表示对局部的具体情况进行数学化［6］，也就是说，情境创设应是数学化中的一部分. 只需要情境创设合理，学生就有可能从现实世界中获得数学知识，用数学的眼光去观察现实世界. 上述案例中首先使学生思考现实情境，初步将现实情境转化为数学问题即數学化的开始.

2. 数学化不等于形式化

将数学化的具体含义直接与其中形式层次画等号，是对数学化的一种认知偏差. 将数学化等于形式化是指一味地将现实问题数学化、强调数学的抽象概括与数学符号化. 在教学中，强调形式化的结果而忽略数学化本该有的“过程”，就会使数学学习变成一种毫无活力的数学知识的生搬硬套. 为了弥合这个认知偏差，需要教师全面正确理解数学化应包含生活化，如弗赖登塔尔所说：“教数学的教室不可能浮在半空中，而学数学的学生也必然是属于社会的.”［6］即我们所学的数学知识终将回到现实中，只有让数学与相关的现实背景紧密相连，学生才能获得富有生命力的数学知识.

3. 均衡的数学化教学是一个寻求过程

弗赖登塔尔将数学教学分为如图7所示的四种情况，对应着四种不同的教学观：（1）横向与纵向数学化都缺乏发展的是机械主义教学观，学习数学枯燥无味；（2）缺少横向数学化、发展纵向数学化的是结构主义教学观，学习充满数学道理，但学生难以体会数学与生活的联系；（3）缺少纵向数学化、发展横向数学化的是经验主义教学观，学习容易陷入模仿，缺乏数学思考；（4）横向和纵向数学化均得到发展的是现实主义教学观，学习既凸显数学本质又富有生活趣味. 在数学教育过程中过于注重横向或纵向数学化的教学都是数学化教学的两极. 而均衡的数学化教学需要教师在不断完善横向数学化教学的同时，加强经验合理化，强化纵向数学化的教学因素［7］，即在两者间找到一个均衡点. 这应是教师的一个追求，需要教师不断去探寻——通过合理把握当下数学教学本身的意义，理解数学知识的同时，考虑结合学生的认知基础来设计数学教学，在不断的动态过程中铺设发展数学教学的“现实主义道路”.

参考文献：

［1］ 张奠宙，宋乃庆. 数学教育概论［M］. 北京：高等教育出版社，2004.

［2］ 中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［3］ 弗赖登塔尔. 数学教育再探——在中国的讲学［M］. 刘意竹，杨刚，译. 上海：上海教育出版社，1994.

［4］ 孙雪梅，朱维宗. 数学化思想及其在数学问题解决教学中的应用分析［J］. 数学教育学报，2010，19（01）：20-22+102.

［5］ 张国祥. 数学化与数学现实思想［J］. 数学教育学报，2005，14（01）：35-36.

［6］ 弗赖登塔尔. 作为教育任务的数学［M］. 陈昌平，唐瑞芬，译. 上海：上海教育出版社，1973.

［7］ 王永. 寻找均衡的数学化——评《a能表示什么》一课的得与失［J］. 人民教育，2006（01）：27-29.