教材资源整合下的课堂教学研究

祝维男

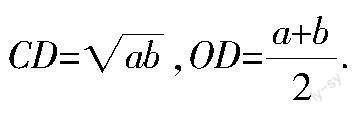
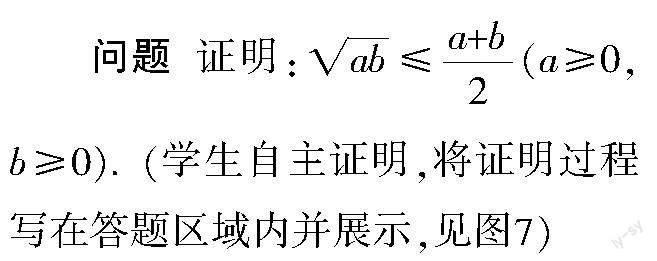
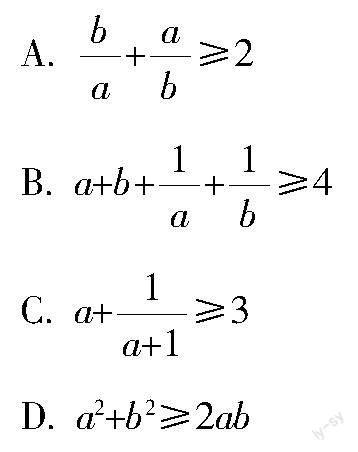
［摘  要］ 整合教材资源的水平是衡量教师能力的重要标志.教师要在深度理解教材资源的基础上，编写出既符合学生认知规律，又体现知识逻辑顺序的教学方案.文章以“基本不等式（第一课时）”的教学设计为例，谈谈教师整合教材资源的方法和作用.

［关键词］ 整合优化；教材资源；基本不等式

教材是依据课程目标和标准要求编写的，是师生开展教学活动的主要工具. 一直以来，大家都比较关注教材的编写理念和设计意图，忽视了日常教学中教师怎样理解教材、运用教材等问题. 事实上，教师不是单纯的教材执行者，而是教学资源的开发者、课堂教学的设计者，整合教材资源的水平是衡量教师能力的重要标志. 在备课过程中，教师应该在深度理解各种教材资源内涵的基础上，对教材内容进行补充、删减、融合、活化，最终巧妙编排出既符合学生认知规律，又体现知识逻辑顺序的教学方案. 下文是整合人教版初中数学教材和高中数学六个版本教材资源编写的“基本不等式（第一课时）”的教学设计.

教学过程与设计意图

1. 情境铺垫，恰当衔接

第14届国际数学教育大会（ICME-14）在上海华东师范大学中山北路校区举办. 大会的会标设计新颖，数学元素丰富，有大家非常熟悉的图形——“赵爽弦图”. （如图1、图2、图3所示）

问题1 在初中阶段，我们就用“赵爽弦图”证明了勾股定理，你还记得勾股定理的学习过程吗？

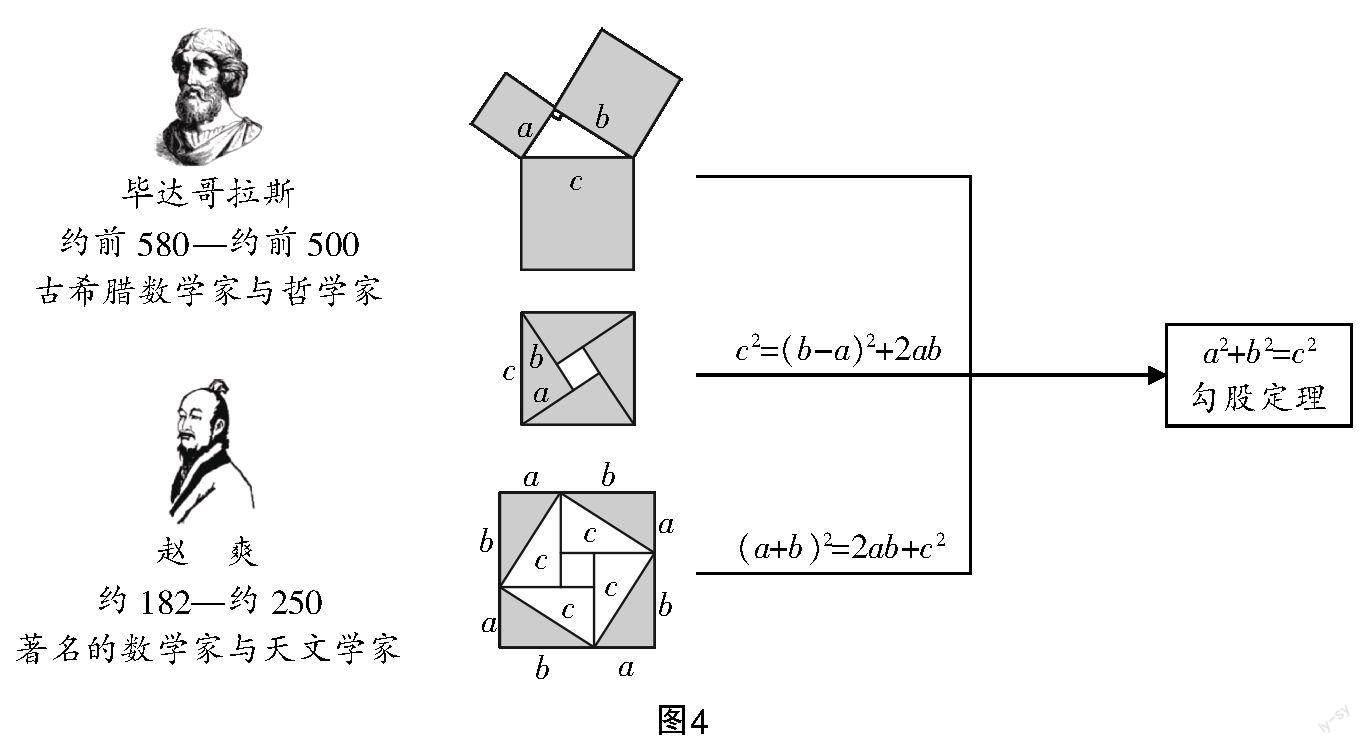
初中教材以“毕达哥拉斯到朋友家作客时，发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系——任何直角三角形，其斜边的平方恰好等于另两边平方之和”这个故事导入新课. 在课堂链接和课本习题中我们用“赵爽弦图”证明了勾股定理. 即大正方形的面积等于小正方形的面积加上四个三角形的面积.

问题2 回顾勾股定理的学习过程，给你带来了怎样的启示？

由形到数，数形结合. 事实上，数学家都是先直观思考问题，然后用演绎的形式进行证明，用文字、数学符号来表达.

设计意图 基本不等式是认识数学、研究数学的工具，基于实际学习的需要，新课标将基本不等式迁移为“预备知识”，起衔接预备作用. 对于基本不等式的导入，各版本教材一直以来都是“五花八门”，并且争议不断. 本节课的导入没有用苏教版的“天平”，也没有单纯用人教版的“弦图”，而是从饱含数学元素的时事背景出发，回顾初中学习勾股定理的过程，为高中学习基本不等式做知识和方法上的准备，解决学生对情境“不熟悉”、高中学习“跨度大”、能力要求“陡升”等问题，自然实现初中和高中的衔接.

2. 问题驱动，结论探究

问题1 通过面积相等得到了等量关系a2+b2=c2，再看“赵爽弦图”，比较面积能发现怎样的不等关系呢？

让各小组合作探究，并展示相关成果.在变动过程中，大正方形的面积始终大于等于四个小三角形的面积和，其中大正方形的面积为a2+b2，四个小三角形的面积和为2ab，所以a2+b2≥2ab.

问题2 在不等式a2+b2≥2ab中，等号何时成立？

a=b是等号成立的充要条件，叫“当且仅当a=b时，等号成立”.

问题3 这个不等式是通过几何图形得到的，你能用代数法证明吗？

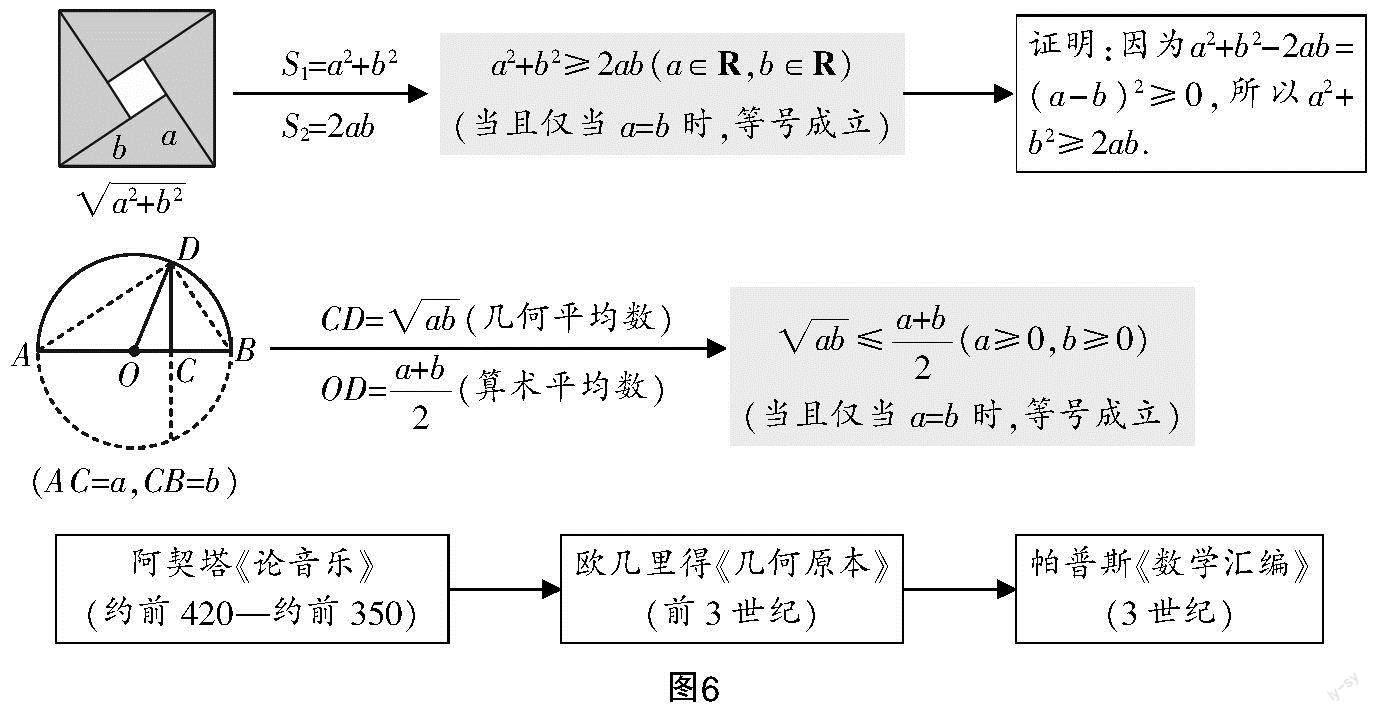
因为a2+b2-2ab=（a-b）2≥0，a∈R，b∈R，所以a2+b2≥ab，将其称为重要不等式.

问题4 下面我们继续看图（见图5），这是一个“半圆模型”，其中AC=a，BC=b，你能求出CD，OD的长度吗？

关系吗？

用GGB动态展示≤，表明正数a，b的几何平均数不大于它们的算术平均数，称之为基本不等式.

含义，逐步发展直观想象、数学抽象等核心素养.

3. 展示交流，代数论证

设计意图 几何的直观验证不能代替代数证明，代数证明可以训练学生的推理能力和计算能力，培养学生的理性思维. 这里通过代数证明既让学生了解不等式证明的常用方法——比较法、分析法、综合法，也让学生知道这三种证明方法之间的关系，提炼证明过程所蕴含的数学思想，引导学生从感性认识上升到理性认识. 比较法、分析法、综合法属于学生必备的数学方法，所以在此借助这个教学环节向学生渗透这些数学方法，为今后学习夯实基础.

4. 理解公式、深化认识

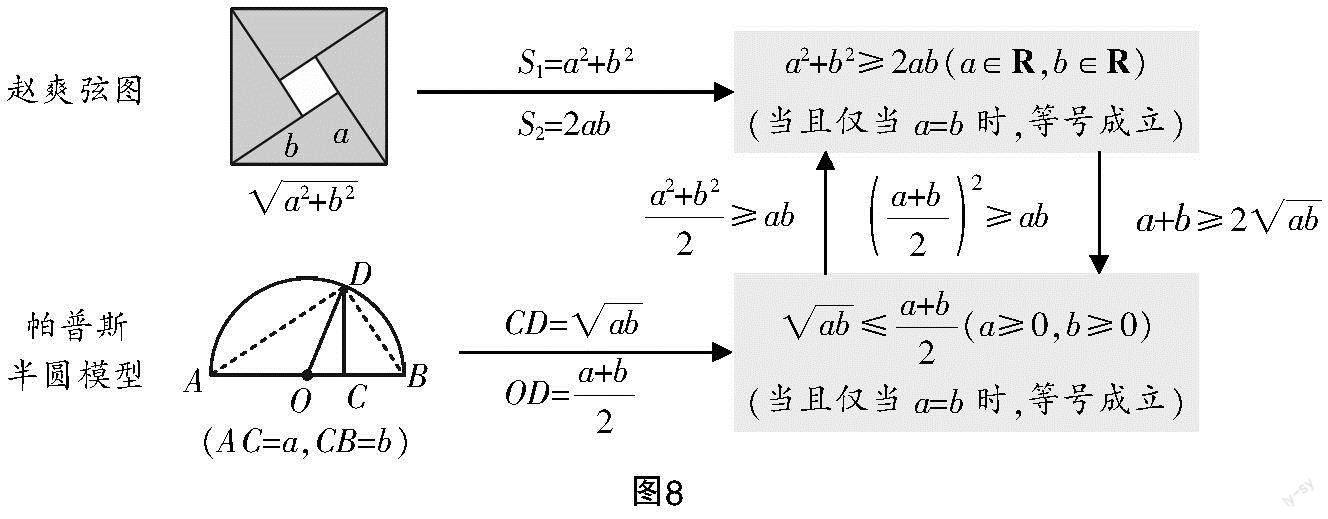
问题 通过由形到数的研究路径得到了两个不等式（重要不等式和基本不等式），这两个不等式之间有怎样的联系呢？（小组讨论）

小组1：研究方法一致，由形到數；等号成立的条件一致——当且仅当a=b时，等号成立.

小组3：结构也是一致的，都反映了两数的和与积之间的不等关系.

（重要不等式和基本不等式之间的联系如图8所示）

设计意图 通过探究重要不等式和基本不等式之间的联系，引导学生关注公式、结论的相互关联，把握基本不等式的本质特征.在转化过程中，掌握重要不等式和基本不等式的常用变形，厘清公式拓展的来龙去脉，理解公式使用的“替换”思想；融合教材中的例题和习题，在基本不等式的推广拓展中，整理知识点，形成公式链，有助于提升学生探究、创新的能力，加深学生的认知广度和深度，也为后续应用基本不等式证明其他不等式以及深入探究基本不等式的变形拓展做好铺垫.

5. 应用公式，巩固提高

习题 （多选题）设a，b为正数，下列选项中正确的有（  ）

设计意图 改编教材例题、习题融合教学，通过“判”“证”“拓”等环节，从结合重要不等式和基本不等式的结构特征进行字母替换，到应用重要不等式和基本不等式进行严格证明，再到提炼重要不等式和基本不等式的常见变形，为后续学习和探究“积定和最小”“多元不等式”“函数最值”等做好充分的准备.

6. 总结提炼，内化新知

（2）学习过程：观察→猜想→证明→应用，从感性认识上升到理性认识.

（3）思想方法：数形结合思想，整体代换思想.

设计意图 一个好的结尾，能画龙点睛凸显一节课的学习重点和问题解决的关键，“变则不变”更让基本不等式的结构美及本质特征呼之欲出.

整合教材資源的方法和作用

1. 整合不同版本教材，实现有效补充

依据《普通高中数学课程标准（2017年版）》重新编写的高中数学六个版本的教材，在编排顺序、编写思路和设计理念上都各具特色. 教师要在备课过程中，通过对不同版本教材的深度阅读，厘清教材内容的编写逻辑，领会教材内容的设计意图. 结合学生的认知水平和认知能力，在比较分析中取长补短，不断丰富教学内容、优化教学设计. 例如人教A版、北师大版等教材是引出重要不等式后再通过替换得到基本不等式的，而苏教版教材则通过“天平称重”直接引出基本不等式，在例题中再用替换的方法得到其他不等式. 事实上，重要不等式和基本不等式可以相互转化，结论的推导方法也相互融通. 本节课融合各版本的教材资源，先以“赵爽弦图”为背景由面积关系的比较得

2. 整合初中、高中教材，体现自然衔接

高中教材与初中教材相比，知识内容增加较多，由浅显变得深奥，由单一变得复杂，思维要求层次越来越高，数学语言也由直观变得抽象. 但是初中和高中的知识是紧密相连的，涉及的数学思想方法是一致的，对概念、公式、定理的探究路径也是相互融通的. 在教学过程中，教师联系初中教材的相关知识、思想方法和探究路径，在系统梳理中找准衔接点，让新知识的推出显得“水到渠成”. 基本不等式是认识数学、研究数学的工具，基于实际学习的需要，以及高一学生的学习能力，基本不等式可以提前学习——新课标下的新教材也把“基本不等式”作为“预备知识”而前置，起衔接作用. 本节课是如何体现初中和高中自然衔接的呢？通过阅读教材发现，初中教材用“赵爽弦图”证明了勾股定理，体现了由“形”到“数”的数学探究过程；高中人教A版教材先用“赵爽弦图”引出了重要不等式，再通过替换得到基本不等式. 所以，从国际数学教育大会的会标中挖掘出“赵爽弦图”导入新课，既融合了数学时事，饱含了数学文化，体现了学科育人的价值，又在知识生成背景、探究路径上找到了吻合的衔接点，符合学生的认知规律，能有效帮助学生从初中数学学习过渡到高中数学学习.

3. 整合教材文本内容，凸现逻辑贯通