考虑整体化层作用的空心板梁桥横向分布计算与承载能力分析
2021-09-09郭建民徐飞萍李广奇刘福忠金泽人
郭建民 徐飞萍 康 良 李广奇 刘福忠 金泽人
(1.山东高速股份有限公司,济南 250014;2.山东省交通科学研究院,济南 250101;3.同济大学桥梁工程系,上海 200092)
0 引言
空心板梁桥在跨度13~20 m的公路桥梁中广泛应用[1]。装配式空心板梁桥梁在数10年的运营使用过程中暴露出了很多问题。由于空心板梁的构造特性,其铰缝和整体化层成为病害频发的区域,典型的病害为铰缝破碎和整体化层的纵向开裂问题[2]。增加或重新铺设整体化层是实现空心板梁桥结构修复和性能恢复的主要方法。
桥梁的横向分布理论已有多年的研究[3-4]。由于构造的特性,装配式空心板梁桥主要通过铰缝和整体化层的传力实现横向连接[5],横向分布系数的计算理论主要为铰接板法。在装配式空心板梁桥的应用初期多采用浅铰缝,能够近似符合铰接板法的这一假定。考虑到浅铰缝难以有效振捣的问题[6],近年来逐步采用深铰缝代替浅铰缝连接各片空心板梁,以保障铰缝混凝土的质量。然而,采用深铰缝的装配式空心板梁桥不再符合铰接板法中只传剪力、不传弯矩的假定,横向传力特性发生显著改变,在计算假定的合理性和计算结果的准确性方面存在明显问题[7-8]。采用深铰缝后,整体化层的力学作用和刚度贡献同样发生改变,有必要重新审视并提出合适的计算模式,以考虑整体化层对横向传力和结构承载力的影响。
针对上述问题,本文尝试建立了一个空心板梁结构的通用力学模型,可以综合考虑板梁铰缝以及整体化层对空心板梁横向传力特性的影响,并通过有限元分析分析计算误差,对该方法进行校验。基于提出的通用力学模型,对旧梁加固过程中整体化层厚度的影响进行了探讨。
1 计算方法
1.1 接缝横向传力模型
本文在计算横向分布系数时,考虑四种不同的接缝横向传力模型:①考虑整体化层的传力作用,整体化层与主梁刚性连接,相邻整体之间的整体化层刚接,主梁相互铰接;②考虑整体化层的传力作用,整体化层与主梁刚性连接,相邻整体之间全刚接;③考虑整体化层的传力作用,整体化层与主梁刚性连接,相邻整体之间全桥铰接;④不计整体化层的传力作用,仅主梁结构铰接。接缝横向传力模型如图1所示。
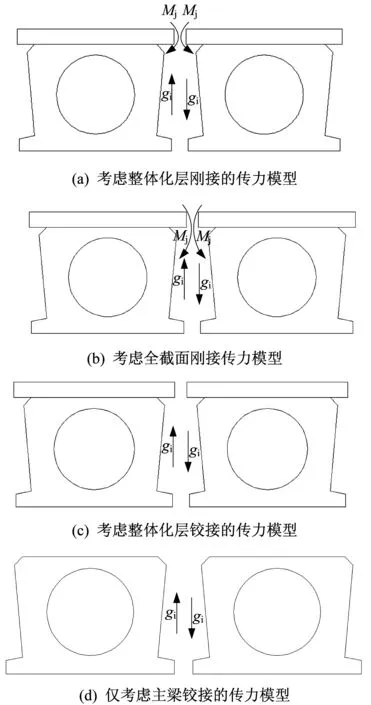
图1 四种接缝横向传力模型Fig.1 Four types of transverse load transferring models of slab beam joint
1.2 横向分布计算方法
采用刚性横梁法计算横向分布系数,根据变相协调方程求得各根主梁影响线,然后求得横向分布系数。
1)考虑整体化层刚接
当考虑整体化层刚接,主梁仍为铰接时,设铰缝之间的剪力从左至右为gi,i=1,2,…,10,整体化层处弯矩从左至右为Mi,i=11,12,…,20。根据变形协调方程,对i=1,2,…,20,均有
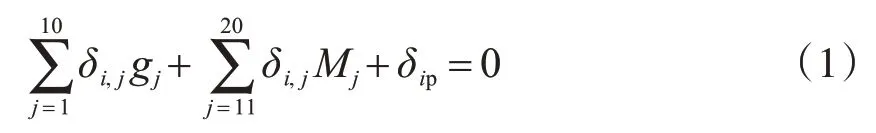
单片空心板在铰缝区域剪切峰值力gi=1作用下产生的影响可由作用在空心板横向中心的竖向力gi=1和扭矩代替,其中b为空心板的半宽。单片空心板在等效半波正弦荷载的作用下在板跨中央产生的挠度为ω,相应扭矩引起的跨中扭转角为α。在偏心正弦荷载作用下的竖向挠度ω与扭转角α分别为
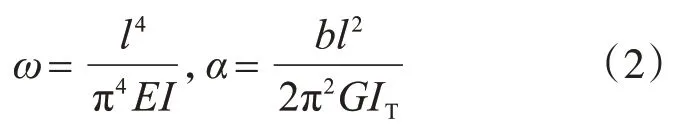
单片空心板在整体化层处弯曲峰值力Mi=1作用下产生整体转角β,板在左侧产生的挠度为,板在左侧产生的挠度为,有

在计算各片梁在弯矩作用下的转角时,考虑整体化层与主梁连接部位为刚性连接,即随主梁产生下挠与扭转。在弯矩作用下,整体化层伸出主梁的悬臂部分转角为

式中:lc为悬臂端长度;h为整体化层厚度。
进而有
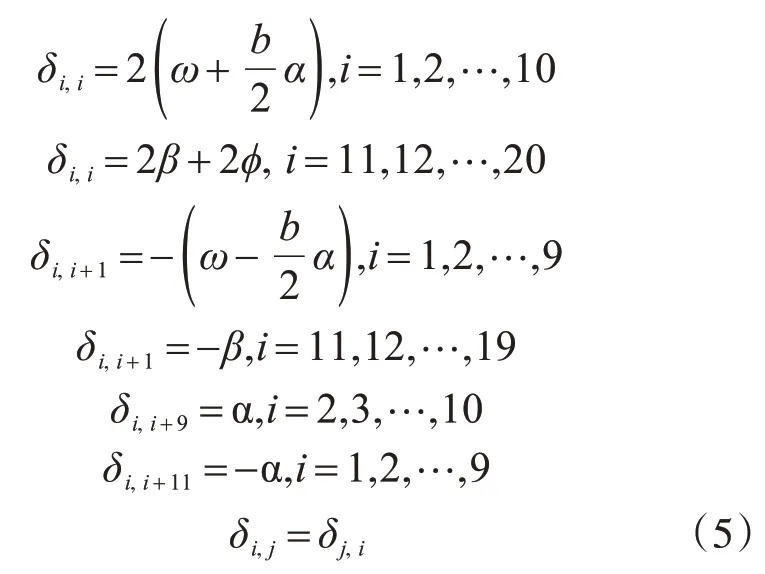
求解第i片梁的影响线时,取

求解得到gi,i=1,2,…,10,进一步求解得到各片梁的反力值,并根据反力互等定理得到各片梁的影响线。
2)考虑全截面刚接
当考虑全截面刚接时,不考虑整体化层伸出主梁的悬臂部分转角影响,即
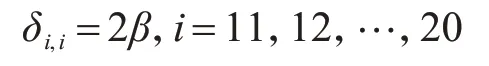
横向分布系数的其他计算过程与考虑整体化层刚接时一致。
3)考虑整体化层铰接
当考虑整体化层铰接时,不考虑变形协调方程中的弯矩分项,则方程退化为对i=1,2,…,10,均有

但在计算偏心正弦荷载作用下的竖向挠度ω与扭转角α中仍应考虑整体化层的刚度贡献。横向分布系数的其他计算过程与考虑整体化层刚接时一致。
4)仅考虑主梁铰接
当仅考虑主梁铰接时,变形协调方程与考虑整体化层铰接时相同,但在计算偏心正弦荷载作用下的竖向挠度ω与扭转角α中不考虑整体化层的刚度贡献。横向分布系数的其他计算过程与仅考虑整体化层铰接时一致。
1.3 方法校验
本文以某16 m跨径典型空心板梁桥为例进行计算分析。桥梁上部结构为2×16 m的装配式预应力混凝土简支空心板,横向布设11片梁。旧梁原有的桥面铺装为10 cm现浇混凝土+6 cm沥青混凝土。桥梁的横断面如图2所示,中梁(6#)和边梁(1#)截面如图3所示。

图2 桥梁横断面图(单位:mm)Fig.2 Cross section of the bridge(Unit:mm)
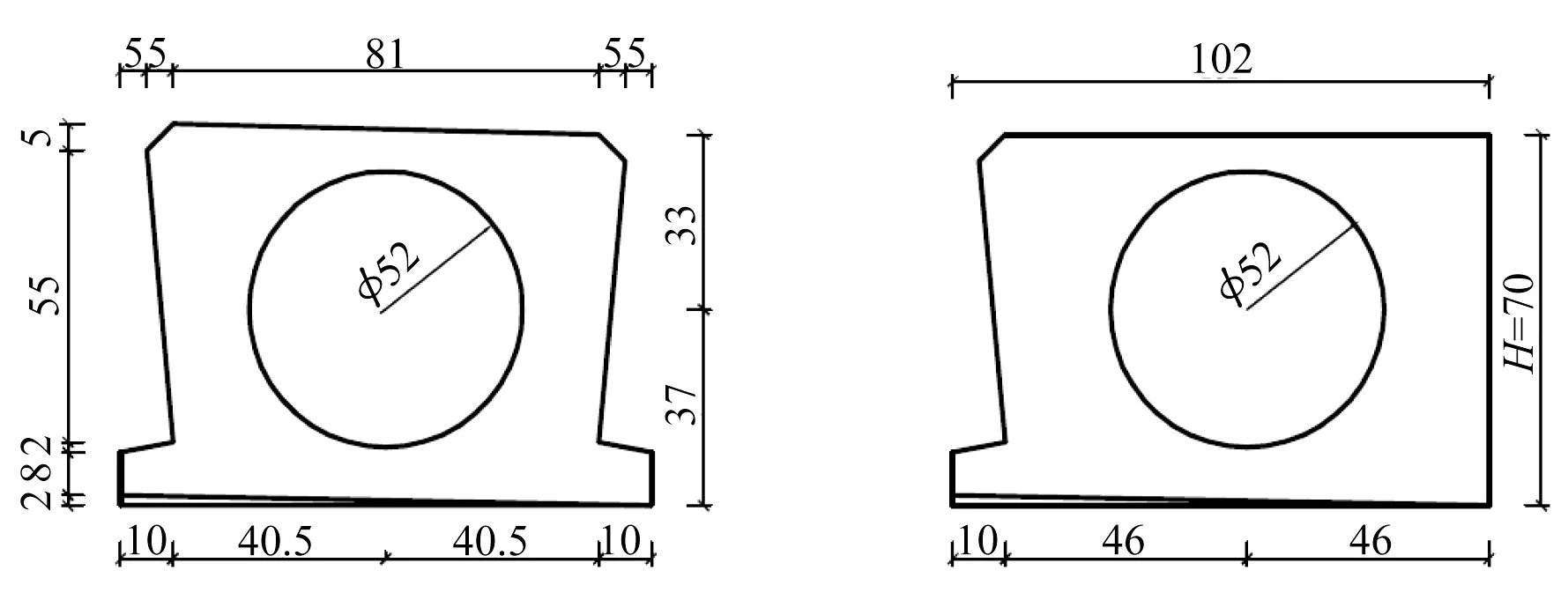
图3 空心板梁中梁与边梁截面(单位:mm)Fig.3 Cross sections of the center beam and the side beam(Unit:mm)
为进行接缝传力的精确分析,采用ANSYS建立了有限元分析模型。模型中预制空心板采用C40混凝土、接缝和整体化层材料采用C50混凝土,混凝土的弹性模量按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2012),分别取3.25×104MPa、3.45×104MPa。混凝土单元采用实体单元Solid45模拟。Solid45为ANSYS中常用的3维8节点结构实体单元,主要用于实体结构的模拟。因本节主要进行受力规律分析,不考虑混凝土结构的继续状态,不考虑裂缝的影响,因此铰缝与主梁之间不设接触单元,未采用Solid65单元,以提高计算效率。有限元分析模型立体图及正视图如图4、图5所示。

图4 有限元分析模型直观图Fig.4 Perspective of the Finite element analysis model

图5 有限元分析模型正视图Fig.5 Front view of the Finite element analysis model
表1对比了采用15 cm整体化层时,不同横向传力模型计算得到的横向分布系数与有限元分析的相应结果。

表1 不同传力模型下各梁横向分布系数Table 1 Transverse distribution coefficients of beams using various load transferring models
由表1可得,考虑全截面刚接传力模型的横向分布系数计算结果与有限元分析结果最为接近(平均相对误差5.5%),其他传力模型的横向分布计算结果相较于有限元分析结果均更为保守。其中,考虑整体化层刚接传力模型的计算结果与有限元分析结果同样较为接近(平均相对误差7.4%),且能有效反映整体化层厚度对横向分布系数的影响,后续将采用这一传力模型进行旧梁加固优化。
2 整体化层影响分析
本文在进行空心板梁桥旧梁加固时,主要通过加铺整体化层增强结构对车辆荷载的横向分布能力(降低了中梁的横向分布系数),并增加截面高度,从而改变了各片梁的受力特性,提高了结构的受力性能。其中,以6号梁(中梁)为分析对象,进行受力性能的优化设计。
2.1 横向传力的影响
根据所述横向分布计算方法,将规范车辆荷载加载于6号梁的横向影响线。其中,车道荷载折减系数按照单车道为1.2、双车道为1.0、三车道为0.8进行计算。最终得到6号梁的横向分布系数,如表2所示。

表2 不同传力模型下6号梁横向分布系数Table 2 Transverse distribution coefficients of Beam No.6 using various load transferring models
根据表2,考虑整体化层刚接的计算结果介于考虑整体化层铰接和考虑全截面刚接之间。仅考虑整体化层刚接时,整体化层厚度越大,6号梁的横向分布系数越小,趋近于考虑全截面刚接的结果。
2.2 承载能力的影响
对于方法校验中所述的16 m简支空心板梁,计算得不同整体化层厚度下的6号梁跨中正截面抗弯承载能力Mu,如图6所示。
由图6所示,随着整体化层厚度的增加,承载能力的增幅逐渐降低。当整体化层厚度为20 cm时,将其提高至25 cm后的Mu增加比例仅为2.4%。此外,随着整体化层厚度的不断增加,承载能力极限状态下,整体化层和预制空心板梁连接面内的剪力不断增大,甚至于超过界面剪切强度。此时,整体化层与主梁始终保持刚性连接的假定不再成立,横向传力特性将发生改变,本文提出的通用力学模型将不再适用。

图6 不同整体化层厚度下的6号梁MuFig.6 Mu of beam No.6 of with different integral layer thicknesses
当整体化层厚度在适当范围内时,旧梁加固优化主要考虑两方面的荷载效应:①空心板梁在自重荷载作用下的受力状态;②为空心板梁在车辆荷载作用下的受力状态。以6号梁跨中弯矩作为受力状态的评价指标,采用接缝横向传力模型a计算横向分布系数,即考虑整体化层对结构的刚度贡献,同时假定相邻整体化层刚接而主梁铰接。
1)自重荷载效应
采用不同整体化层厚度时,6号梁在自重荷载作用下的跨中弯矩计算结果如表3所示。

表3 自重荷载作用下的6号梁跨中弯矩Table 3 The mid-span bending moments of beam No.6 under the effect of dead load
2)车辆荷载效应
在计算车辆荷载作用下单片梁结构效应的基础上,乘以考虑整体化层刚接(即接缝横向传力模型a)的荷载分布系数,得到6号梁在车辆荷载作用下的跨中弯矩,如表4所示。

表4 车辆荷载作用下的6号梁跨中弯矩Table 4 The mid-span bending moments of Beam No.6 under the effect of vehicle load
2.3 加固优化策略
随着整体化层厚度增加,自重荷载效应增大,同时,横向分布系数降低导致车辆荷载效应减小。为衡量整体化层厚度对结构受力的影响,定义活载富余值
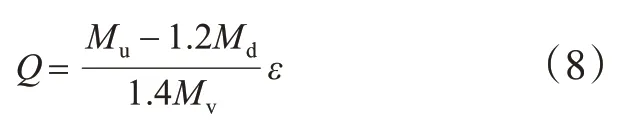
式中:Mu为主梁跨中弯矩承载能力;Md为自重荷载下跨中弯矩;Mv为车辆荷载下跨中弯矩。
计算得到不同整体化层厚度下的6号梁的活载富裕值Q,如表5所示。

表5 不同整体化层厚度下的6号梁Q值Table 5 Q values of Beam No.6 of with different integral layer thicknesses
随着整体化层厚度增加,Q值也相应增大,活载储备较多。这说明考虑整体化层的刚度贡献并假定相邻整体化层刚接时,整体化层厚度越高,结构受力状态越好。同时,整体化层厚度增加导致截面高度增加,增大了桥梁建筑高度和加固造价,为综合考虑结构受力状态和建造经济性,定义参数P

式中,h为主梁高度。
可以认为,参数P值越大,加固方案的优势越显著。表6给出了不同整体化层厚度对应的P值。

表6 不同整体化层厚度对应的P值Table 6 P values of beam No.6 of with different integral layer thicknesses
由表6可知,P值随着整体化层厚度的增加,先增大后减小,在整体化层厚度为20 cm时达到最大,此时整体化层的加固方案最优。
3 结 论
(1)根据有限元分析结果,整体化层厚度对空心板梁的受力状态和变形状态均有较为显著的影响;
(2)采用不同的接缝横向传力模式时,整体化层对横向分布系数计算中的刚度贡献存在差异,其中不考虑整体化层作用和考虑全截面刚接是考虑整体化层影响的两种极限情况;
(3)基于对不同接缝横向传力模式的对比分析,考虑全截面刚接传力模型与有限元分析结果最为接近,能够较好地反映车辆荷载作用下各片梁的荷载分配情况;
(4)同时考虑空心板梁受力性能和经济性的影响,在旧梁加固中采用20 cm厚的整体化层为最优选择。
