逆向思维，探寻解法

季学平

［摘  要］ 逆向思维，就是反方向思考，与正向思维相反的思维方式. 逆向思维的培养，可以丰富学生的思维模式，拓宽解题途径，提升解题能力. 在数学教学中，培养学生的逆向思维，也是提高学生数学素养的一个重要方面.

［关键词］ 初中数学；逆向思维；解题策略

初中数学学到九年级，已从直线型几何图形拓展到曲线型几何图形. 随着所学几何图形的不断增多，所学的与几何图形相关的知识点也逐步增多，几何综合题的难度也逐渐提升. 虽然学生对于几何综合题也积累了一定的解题经验和解题技巧，但还不够全面，仍需在教与学中进一步拓宽解题途径，提升解题能力.

多数学生做几何综合题时都习惯从问题的正面入手，将教师课堂上讲过的知识应用到其中，这种解题方式很容易固化学生的思维，会阻碍学生创新思维能力的发展，也会影响学生的临场发挥，不理想的成绩甚至会影响学生学习的积极性和信心. 笔者在九年级上学期的期中练习时遇到了一道圆的综合题，学生的解答情况非常不理想，问题出在哪里？在随后的解析教学中，笔者找到了原因.

原题重现

试题 已知AB是☉O的直径.

（1）如图1所示，C，D两点均在☉O上，且BC=BD，CD=AD，求证：∠ADC=2∠BDC.

（2）如图2所示，点C在☉O上. 若点D是平面内任意一点，且满足AD=CD，∠ADC=2∠BDC.

①利用直尺和圆规在图2中作出所有满足条件的点D（保留作图痕迹，不写作法）；

②若AB=4，BC的长度为m（0<m<4），点D的个数随着m值的变化而变化，直接写出点D的个数及对应的m的取值范围.

学生困惑

在以往的教学中，数学综合题已有一定的训练，学生已经初步积累了一些解题经验. 综合题的第（1）题难度一般较低，学生有能力解决，同时建立基础模型为后续问题的解决提供解题思路或方法参考，从而能拾级而上.

多数学生能想到不同方法完成第（1）题的证明，但很快发现，第（1）题的解题思路无法与后续问题关联起来，不能为后续问题提供任何帮助，更没有以往拾级而上的轻松感受，从而让多数学生困惑不已. 在解析教学中，笔者让学生充分发言，各自发表了解决第（1）题的不同解法，并逐一详细板书.

首先由生1提出最基本的解法：

如图3所示，连接OC，OD，AC后，先由BC=BD，OC=OD得AB垂直平分CD，进而得AD=AC，再结合AD=CD

当生1的解法完整板书后，得到了其他学生的肯定，同时也有学生提出这种解法的辅助线太多了，其实只需要作两条，故有了生2的解法：

生2的解法利用了图形中三角形的特殊性，求解了相关角的特殊值，当这种解法完整板书后，又有学生提出了还可以简化.

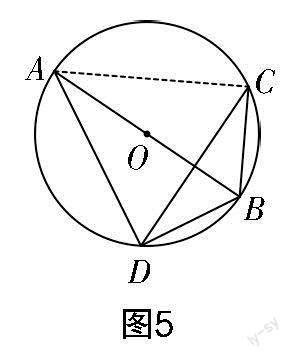
生3提出只需要作一条辅助线，具体解法如下：

如图5所示，连接AC，由BD=BC得∠BCD=∠BDC；由AB为☉O的直径，可得∠ACB=90°，进而可得∠ACD=90°-∠BCD；由AD=CD得∠CAD=∠ACD，进而可得∠ADC=180°-2∠ACD. 于是不难得出∠ADC=2∠BCD. 又因∠BCD=∠BDC，故可证∠ADC=2∠BDC.

在前三种解法的交流中，学生的思维全面打开，在生3的思路基础上，很快就有了生4的解法：

综合4名学生的解法不难看出，学生对综合题的解决没有整体性思考，没有全局观，往往只对题目所给的基础模型进行简单思考，不与后续问题综合考虑，轻易答题，或因基础题（即第（1）题）的解决方法众多，而没有找到真正与后续问题有关的解题模型，无法为后续问题提供有效的支持，从而面对后续问题束手无策.

問题解决

在肯定几名学生的解题思路后，笔者带领学生分析这几种解法能否为下面的问题提供帮助，结果发现这几种解法都无法为下面的作图提供帮助. 故对于综合题来说，基础问题的确可以有多种解决方法，但哪一种方法才能为后续问题提供方法指导才是解题的重点，因为，解决综合题时，首先要通读整个大题，把几个问题全部了解清楚. 有了基础问题的解决思路后，不应急于动手书写，而应适当逆向思考，从后续问题逆向对基础问题进行深入探究，思考后续问题与基础问题的关系，挖掘前后问题之间的共性，分析其中的关联，建立有效的基础问题模型，这样才能使后续问题变得简单.

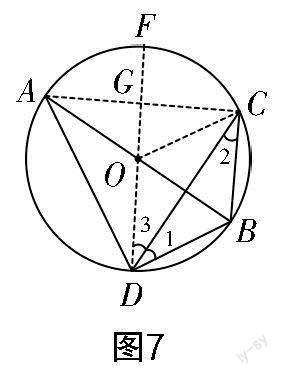
实际教学时，笔者引导学生分析第（2）题，由“AB是☉O的直径”“点C在☉O上. 若点D是平面内任意一点，且满足AD=CD，∠ADC=2∠BDC”“尺规作图求点D”可知，图1完全满足作图要求，是众多作图结果中的一种，此时点D恰好在圆周上，就这种特殊情况做进一步分析，有如下结果：

如图7所示，AB是☉O的直径，点C在☉O上，因此，连接AC后，可得∠ACB=90°，即AC⊥BC；由DA=DC，OA=OC，可得OD所在的直线是AC的垂直平分线，DG⊥AC，从而可得DG∥BC. 进而可得∠2=∠3，同时，根据等腰三角形的三线合一性质，可得∠ADC=2∠3，由此通过等量代换得到∠ADC=2∠BDC.

结合基础模型，就不难找到第（1）题的解题策略和第（2）题的作图思路. 分析完成后，学生们很快就给出了两个小题的解答.

（1）如图7所示，

连接AC，OC，连接DO并延长交AC于点G.

因为OA=OC，DA=DC，

所以DG⊥AC，AG=CG.

所以∠ADC=2∠3.

因为AB是☉O的直径，

所以∠ACB=90°.

所以BC⊥AC.

所以DG∥BC.

所以∠2=∠3.

因为BD=BC，

所以∠1=∠2.

所以∠1=∠3.

所以∠ADC=2∠1，

即∠ADC=2∠BDC.

（2）①作图思路：由DA=DC可得点D一定在AC的垂直平分线上，所以先连接AC，作其垂直平分线. 由AB是☉O的直径，且无论C在何处，都有DO∥BC，故再需BD=BC，所以再以点B为圆心、BC的长为半径作圆，与AC的垂直平分线的交点即为点D，如图8所示.

教学反思

当学生完成第（1）题和第（2）①题的作图后，笔者又带领学生回顾此题前后问题之间的关联，让学生畅言本题带给大家的感受和总结的经验. 学生的总结如下：

通过这道题的学习，我们有了新的解题体会. 综合题多个小题之间一定存在解法策略上的联系，这一点在以前的学习中我们就有体会. 以前遇到综合题，我们基本上会正向思考，拾级而上，第（1）题的解题策略清晰，解法不多样，且难度不大，这就给第（2）题的解题指明了方向，能为后续问题提供准确的解题思路，只是考点不同，难度增加，解题过程复杂些. 圆的知识点较多，与其他知识结合后，同一问题的解题策略不再单一，方法多样，可谓“条条大路通罗马”. 众多方法并不能都为后续问题提供解题方向或解题策略，因此，解决综合题时，我们更应该通读整个问题，必要时从后续问题中寻找与基础问题之间的关系，挖掘前后问题之间存在的共性特征，适当逆向挖掘综合题的解题方法，这样会有意想不到的收获.

在此题的解析教学中，笔者也和学生一同成长. 在解题设计时，笔者就要考虑引导学生从哪些角度去思考、分析问题. 在实际教学中，笔者则坚持以学生为中心，解析问题的过程中引导学生学会正面遇阻而不得时，尝试逆向思维，从后向前，挖掘前后问题之间的联系，尝试反向倒推，进而寻找解题方式，建立基础模型. 在数学教学中培养学生的逆向思维也是提高学生数学思维能力的一种重要方法，且可以使一些难以解决的问题迎刃而解，这对于提高学生灵活运用数学知识分析问题、解决问题有很大的帮助.