关注图形结构，挖掘隐含模型

朱来娟

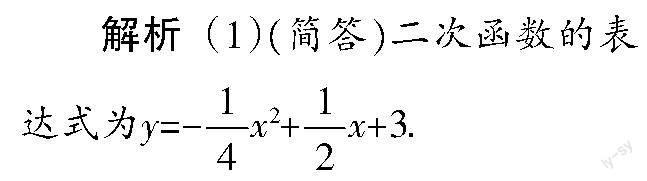
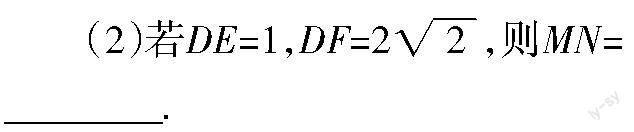
［摘  要］ 几何综合题中往往隐含了重要的模型，合理利用模型可简化解题过程，降低思维难度. “一线三垂直”模型在解题中十分常见，其模型结论是串联线段、角度条件的关键. 文章结合实例全面呈现模型探究的过程.

［关键词］ 几何模型；一线三垂直；相似；全等

几何模型是对图形特殊结构、特征的提取与重组，模型中的结论是图形本质特性的体现，合理利用模型可有效提升解题效率，因此探究解题时有必要关注其中的隐含模型. 下面对一道2022年中考几何真题进行探究.

试题探究

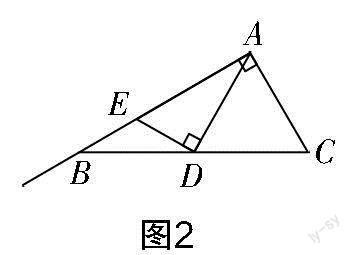
试题 （2022年扬州市中考数学卷第36题）如图1所示，在△ABC中，∠BAC=90°，∠C=60°，点D在BC边上由点C向点B运动（不与点B，C重合），过点D作DE⊥AD，交射线AB于点E.

（1）分别探索以下两种特殊情形时线段AE与BE的数量关系，并说明理由：

①点E在线段AB的延长线上且BE=BD；

②点E在线段AB上且EB=ED.

（2）若AB=6.

②直接写出运动过程中线段AE长度的最小值.

解析  （1）该问探索AE与BE之间的数量关系，要基于设定条件进行推导.

②当点E在线段AB上时，如图2所示，因为EB=ED，所以∠EBD=∠EDB=30°，∠AED=60°. 在Rt△ADE中，∠EAD=30°，则AE=2ED. 所以AE=2BE.

（2）该问设定AB=6，分别设问求AE的长，可结合具体图形分析.

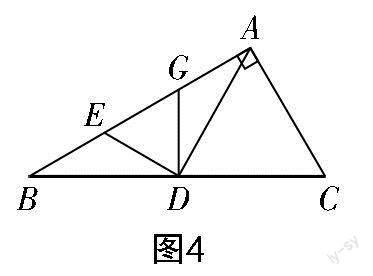
①分别过点A，E作BC的垂线，垂足分别为H，G，则∠EGD=∠DHA=90°，如图3所示.

模型挖掘

1. 模型提炼

上述第（2）题第①问，通过推导出∠GED=∠HDA，∠EGD=∠AHD=90°，证明了△EGD∽△DHA. 挖掘图形特征，有两大特点：①△EGD和△DHA均为直角三角形；②∠EGD和∠AHD的一条直角边共线（GD和DH共线）.

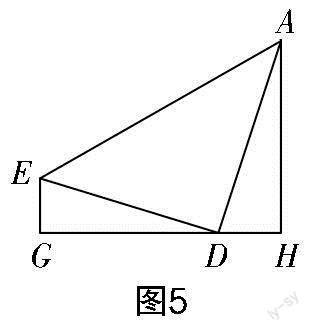
实际上有直角边共线的直角三角形构成了“一线三垂直”相似模型. 提取其中的图形，如图5所示. 根据模型的特征条件，始终可以获得三角形相似的结论.

已知：∠EGD=∠AHD=∠EDA=90°.

结论：△EGD∽△DHA.

因此实际求解时，挖掘图形的直角及共线特性，确定为“一线三垂直”相似模型，即可直接推得相似結论.

2. 模型拓展

对于上述三角形相似关系——△EGD∽△DHA，结合全等判定可知，若添加一条边相等，则可以进一步转化为全等关系——△EGD≌△DHA，从而构建将“一线三垂直”相似模型上升为“一线三垂直”全等模型，该模型中的两个三角形为全等关系，且所夹三角形为等腰直角三角形.

已知：∠EGD=∠AHD=∠EDA=90°，GD=AH（或EG=DH或ED=AD）.

结论：△EGD≌△DHA.

<D：＼数学教学通讯中旬＼2023数学教学通讯中旬（09期）＼2023数学教学通讯中旬（09期） c＼aa-1.jpg> 关联探究

“一线三垂直”相似模型或“一线三垂直”全等模型在实际解题中有着广泛的应用，基于模型特性可直接推导两三角形的相似关系或全等关系. 解题时可分两步进行：第一步，解析问题条件，构建或提取复合图形中的模型；第二步，根据模型得出两三角形相似或全等，进而推导出等角或等线段. 下面结合实例进一步解读探究.

1. “一线三垂直”相似模型的应用

例1  （2022年无锡市中考卷第28

（1）求该二次函数的表达式.

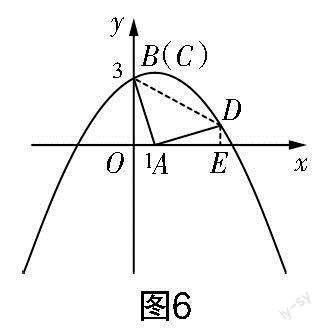
（2）若点C与点B重合，求tan∠CDA的值.

（3）点C是否存在其他的位置，使得tan∠CDA的值与（2）中所求的值相等？若存在，请求出点C的坐标；若不存在，请说明理由.

（2）过点D作x轴的垂线，垂足为E，连接BD，如图6所示.

（3）根据题设要求探寻符合条件的点C位置，再利用复合图形的性质，求出对应点C的坐标即可，过程略.

评析  上述第（2）问中△ADE和△BAO构成了“一线三垂直”相似模型，该问题属于含隐性模型的问题，即原图形中模型结构不全，需要通过作辅助线来加以补全. 因此利用模型解题时需要分两步：第一步，首先提取模型，确定模型是否完整，若不完整则需补全；第二步，根据模型特性推导结论，结合题设条件解题.

2. “一线三垂直”全等模型的应用

例2   如图7所示，四边形ABCD是正方形，点E在边AD上，△BEF是以E为直角顶点的等腰直角三角形，EF，BF分别交CD于点M和点N，过点F作AD的垂线交AD的延长线于点G. 连接DF，请解答下列问题：

（1）∠FDG=________；

解析  （1）因为四边形ABCD是正方形，所以∠A=90°，AB=AD. 因为FG⊥AG，所以∠G=∠A=90°. 又知△BEF是等腰直角三角形，所以BE=FE，∠BEF=90°. 分析可知，在图7中，∠G=∠A=∠BEF=90°，BE=FE，构成了“一线三垂直”全等模型. 由模型特性可得△ABE≌△GEF，所以AE=

评析  上述第（1）问中△ABE和△GEF构成了“一线三垂直”全等模型，模型中BE=EF，使得两三角形在“相似”基础上具有了“全等”特性. 需要注意的是，“一线三垂直”全等模型中所夹三角形必然为等腰直角三角形，因此探究解析时要关注其中的特殊三角形.

教学思考

上述基于考题开展模型挖掘，探究了“一线三垂直”的两类模型，其探究及应用过程有一定的参考价值，下面基于教学实践进一步思考.

1. 关注图形结构，生成几何模型

几何问题中往往融合了一定的数学模型，合理利用模型可以提升解题效率，但教材中一般不会针对性讲解，需要独立探究，总结生成模型. 因此教学中，教师要合理安排教学环节，引导学生亲历模型探究的过程，从复合图形中提取模型，总结模型结论. 一般可分四大环节：环节一，初识模型，引导学生结合所学证明例题；环节二，感知结构，让学生对比例题中的图形结构，初步感知模型；环节三，总结模型，引导学生总结模型的结构特征，生成系统的几何模型；环节四，强化应用，结合实例开展模型应用，让学生掌握模型应用的方法.

2. 适度拓展模型，生成模型关联

几何模型是基于几何特性的提炼与凝结，一些模型之间具有一定的关联，通过设定条件可以实现相互转化. 以上述“一线三直角”模型为例，将模型中的“直角”替换为“一般角”时，则转化为常规的“一线三等角”模型；“一线三直角”相似模型中增加“一组对边相等”则可以生成“一线三直角”全等模型. 因此模型教学中教师还应注重拓展，可从“关联模型”和“类似模型”两大视角进行：在“关联模型”探究中进行知识链串接，引导学生延伸模型；在“类似模型”探究中，引导学生进行模型延伸，总结类型模型，如相似模型中的“A”形相似模型、“8”形相似模型. 通过模型拓展探究，让学生深入、全面地了解模型.

3. 注重实际应用，总结应用技巧

开展模型探究的最终目的是为了应用解题，因此引导学生掌握模型应用的方法技巧是重点. 教学中可从三个方面来引导：一是证明模型特性，让学生掌握模型原理，充分理解模型，强化认识；二是结合实例，即结合各类实际问题，引导学生亲历模型解题过程，从“读题审题”“模型提取”“特性应用”三个环节感知应用；三是细节讲解，通常“模型提取”环节有一定的难度，需从复合图形中提取模型，尤其是隐形模型需要补全，教师要指导学生掌握补全的方法，整体把握模型，局部作图补全，从而使学生充分掌握模型应用的方法.