从通法到通性：追求解题的自然属性

姚春珍

［摘  要］ 中考复习需注重思维的发生过程，要从通法到通性，追求解题的自然属性. 教师进行中考复习时，要通过试题演练，使所有学生有不同的发展，要通过理思路、探方法来找到通法，从善总结、悟方法过渡到通性，最后深化到提升能力，从而提高复习的实效性.

［关键词］ 中考试题；自然属性；通法通性；复习实效性

目前，不断有研究“自然解法”的文章出现，但大都基于解题学微观层面探讨自然“通法”，缺乏对解题学教学论的中观研究. 而中考数学试题作为解题学的主导方向，对课堂教学起着“自然性”思想统领作用，因此，立足于系统常规研究试题的“通性”维度更具有前瞻意义.

就存在哲学范畴而言，“自然”取自然而然之意，即按照事物内部规律而发展变化. 北京林业大学王向荣教授认为，自然性包括原始的自然、生产的自然和美学的自然. 把自然界的这种自然性借用到教学论领域，则需要追求解题的自然属性［1］. 下面以2019年苏州市中考数学试题第25题为载体，呈现解题探究的自然性，凸显“崇尚自然和常规”的自然要义，引导自然课堂素养教育的实践行为.

试题呈现

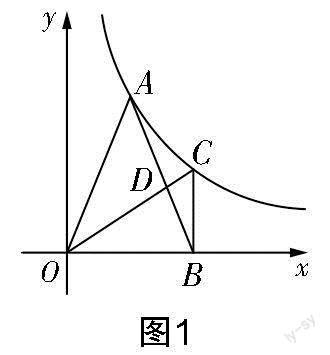
本题重点考查反比例函数、等腰三角形、勾股定理以及相似等知识. 本题为学生提供了综合知识抒发见解的学习窗口，学生可以从已有的经验出发，将学习的知识概括成问题，然后创设出与认知相冲突的问题，接下来为解决冲突而继续深究，从而使问题重新明朗化. 在以此题为线复习函数中档题的过程中，笔者发现学生对于第（2）问的求解方法有多种，这体现了学生在初中阶段学会了用不同的思维方式思考问题，用不同的方法攻破问题，会综合运用数学知识解决问题，体现了学生的应用意识和创新意识. 此题既体现了初中数学教学知识的着落点——从通法到通性，找到解题的自然属性，又彰显了核心素养在初中数学这块知识土地上落地生根，培养了学生的实践能力［2］.

解法探究

1. 找寻常规思路，剖析图形本质，实现自然回归

寻求常规解题思路，需要溯源比较. 溯源比较是解题的基本维度，反映解题学系统内部的自然属性. 这里的“溯源”是对问题来源的哲学追问；“比较”是对研究方法的认证，带有定量分析到定性把握的自然特征. 这就是齐民友先生所认为的解题要“回到自然”，而“回到固有的生动活泼的思考”也是克莱因大师的数学遗风. 因为生动活泼思考心理状态是溯源比较的意义结果［3］，可见自然属性包括溯源比较的本体特征，是自然解题教学论的起点.

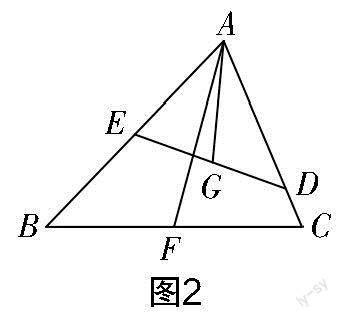
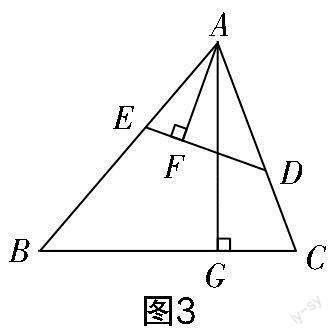
教材上的练习题综合考查了相似三角形的判定与性质、线段的中点、分数的基本性质等知识，要求学生重点掌握相似三角形的判定与性质. 学生探究出“相似三角形对应中线的比等于相似比”后解决此题便比较容易上手. 教师上课讲解时可加入变式，目的在于让学生掌握求解的自然属性. 前面的中考题与教材上的练习题，图形本质是相同的，因此学生很容易想到用相似三角形的性质来求解中考题第（2）问.

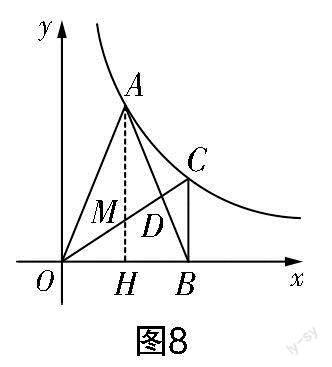
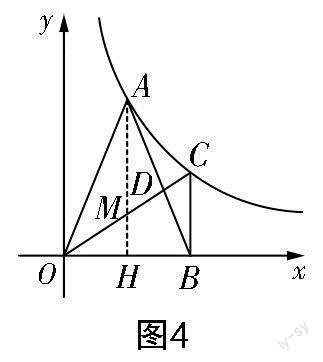
如图4所示，过点A作AH⊥x轴，垂足为H，AH交OC于点M. 因为BC⊥

本题考查了学生的知识技能、数学思考能力及问题解决能力，运用此种解法求解的学生，说明他们的数学基础知识扎实，基本技能达成度较好.

从问题溯源的角度来看一个城市（苏州市）连续两年考查同一个基本图形的客观事实，2020年的苏州中考卷第10题、2021年的苏州中考卷第24题均为一次函数、反比例函数的综合运用，因此研究解题的自然属性为试题研发提供了方向和趋势，敞亮地呈现了试题的来龙去脉和立意关联，反映了命题本源的自然属性，揭示了比较研究的意义在于发散思维的自然过渡，从而实现试题的自然回归.

2. 巧添辅助线，转化比值，实现自然联想

解题过程中学生应综合运用数学知识. 知识点在教材中是静态呈现的，但在解题运用中是动态生成的. 在复习阶段，教师应从整体上把握教学内容，让学生从知识结构上将内容进行整合，将知识进行统筹，将方法进行内化，从而实现解题的自然联想. 添加辅助线，是学生运用所学知识解题时质的飞跃的体现. 复习阶段，教师应遵循量力性原则，让学生感悟数学知识的关联性、整体性，从而实现自然联想，实现自然解题的发展.

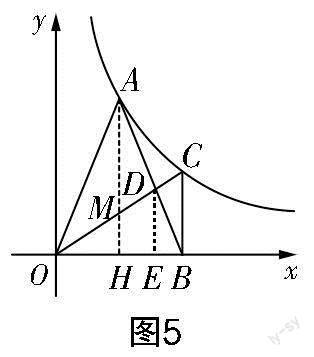
解法二：学生在解得C（4，3）后，并没有直接求出交点M的坐標，而是运用“平行线等分线段定理”求线段MH的长度或转化成线段的比来求MH的长度.

学生把求线段AM长度的解决思路和方法进行了迁移，不是中规中矩地运用常规方法，而是另辟蹊径，让计算量相对减小. 有的学生解得点D的坐标后，过点D作x轴的垂线，运用“平行线分线段成比例定理”将比例进行转化. 学生解得点D的坐标后，想到求比值用相似比，于是回到出发点. 在作高的过程中，学生得到比例的性质，可谓“植一木，成一林”. 解题中体现了用几何直观和空间想象来理解数学，更体现了学生将知识转化为能力.

从自然属性出发，在从“解决什么”到“学到什么程度”的过程中，研究解题的自然联想为解决此类问题指明方向，提示“转化”思想，过渡到自然联想. 此类解法使学生学会思考，解题稳重而又不失方法灵活. 学生基础知识和基本技能达到一定程度时才能得到自然联想，上述求解过程充分体现了学生分析问题和解决问题的能力，学生的推理能力和几何直观等核心素养培养也落到了实处.

3. 借助相似三角形，寻求通法通性，实现自然建模

学生在寻求更高层次的解题思路时，会经历综合运用知识的过程，掌握解题方法，拓宽研究问题的思路，会有新的认识，新的生成，新的思维突破，并形成通法通性，实现自然建模，最终培养学生的基本素养. 学生求线段的长度时，借助相似三角形构造模型，可见自然属性应包括通法通性的特征，实现自然建模，实现自然解题教学论的飞跃.

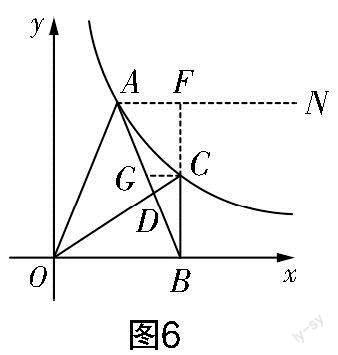
解法三：学生发散思维，在AB的右侧构造“A”形相似三角形，使计算量减小.

学生通过两次构造相似三角形来求解，即在AB右侧构造图形，使计算简单，将问题转化为一个合适的数学模型，体现了学生对相似三角形知识有较强的综合运用能力. 此解法培养了学生的发散思维，并通过问题重新构造模型，体现了学生的数学建模素养.

解法四：学生通过构造“X”形模型找相似.

学生的思维非常活跃，为找相似，顺其自然地想到了构造“X”形相似. 由数到形，培养了学生的空间想象能力和抽象思维能力. 学生采用上述解法，说明学生平常学习中注重实践探究，体现了学生思维的广阔性和灵活性，更体现了学生的想象能力很强，数学建模也搭建得比较成熟.

从问题通法通性角度解答此类中考题，从题目的适宜性、生成性、创生性角度出发评析此类题目，此题难度不大，兼顾了所有学生，让学生都有所体悟，因此起到了“以题知法”的作用. 此题可以作为数学复习阶段的原始素材，然后延伸教学内容，拓宽思维，寻求通法通性，实现自然建模，最终得到试题的自然回归.

4. 借助参数，由特殊到一般，实现自然顺应

寻求解题的一般性思路，能真正掌握数学知识内在联系和本质特征，积累数学学习经验，最终得到自然顺应. 数学知识的获得不能局限于某一个点，应从解决问题背后隐藏的思想方法中挖掘，内化为方法，用这种方法去研究和解决新问题，从而使问题螺旋式上升，方法螺旋式升华［4］. 可见自然属性应包括一般性原则，实现自然顺应，实现自然解题教学论的升华.

解法五：有少量学生将点A看成动点，运用参数k来解决问题.

此解法与解法三有相同之处，但绕开了k的具体数据. 可以说在如此短的时间内将数学“从特殊到一般”思想达到融会贯通的地步，是学生“学习能量”和核心素养积累到一定程度才能达到的境界，其能为学生的创新意识培养和可持续发展奠定基础.

从问题一般性原则出发讲述同一知识考查的客观内容，从“特殊到一般”的数学思想蕴含数学的一般性观念，能提升对知识点和方法的深度理解，将方法内化于心，将数学思想转化为数学策略，从而实现自然顺应，实现知识的自然属性回归.

教学启示

中考真题作为复习阶段的原始素材，有重要的引领作用，教师如何在课堂分析中进行客观呈现，如何将解题的自然属性进行呈现，如何将试题的通性进行体现都非常重要，真题讲解将引领课堂自然生成.

1. 理思路，探方法

教师的作用在于提升学生的认知高度，复习的任务还在于“发展”，即知识得到新的发展，学生得到新的发展. 很多试题，表面上看是新题，但同旧题的求解方法差不多. 这打破了教师和学生的惯性思维，促使师生共同探索，教学相长，其乐无穷.

2. 找通性，善总结

复习的任务在于系统整理、融会贯通. 上述试题唤醒了学生已有的解决函数的经验，运用构图直接求解或运用转化等方法，都是找通性，让零散的知识一一再现. 上述过程，学生通过解题，将原有的知识点形成系统的知识网和思维网，从“找模型—建模型—解模型—用模型”的通性中去解决问题，并总结经验. 解题复习，能增强学生对数、形的整體认识，能使知识达到系统性、连贯性和可持续性，同时有利于将学生从茫茫题海中解脱出来，达到事半功倍的学习效果.

3. 悟方法，提能力

函数中考题一般从基本图形出发，转化为求交点问题、相似三角形，最后得到一个简单的模型. 这体现了数学中从特殊到一般的数学思想方法，能促进学生把问题想深想透，将思维与实践引向更深远处.

在平时的复习教学中，教师不仅要关注问题的解决，要教给学生解决问题的各种方法和策略，更要注重学生数学核心素养的落实和提高. 在平时的教学中，教师要让学生多训练一题多解，要引导学生总结解题用到了哪些方法，是否有更特殊的解法，这些解法有没有共同点……这样学生就会对不同的解法进行比较，养成从不同角度思考问题的习惯，并找到此类题的通性通法. 所以，教师在平时的教学中应该多展示一些能够锻炼学生数学思维的真题，多渗透一些解决问题的思想，找到解题的自然属性.

《义务教育数学课程标准（2022年版）》指出“形成重论据、有条理、合乎逻辑的思维品质，培养科学态度与理性精神”［5］，此类中考题正好呼应了新课标. 不同的学生用不同的思维解题，考查了全体学生应该达到的课程目标的基本要求，同时考查了不同学生用不同的策略. 解题教学要既面向全体学生，又关注学生的个体差异；既用常规思路，又找到通法通性，体现不同差异学生的核心素养的养成. 此类中考题将思想贯穿题中，将直观想象、数学建模、数学运算等核心素养隐藏于解题中，找到解题的自然属性，让所有的学生都能参与到解题中，实现“不同的人在数学上得到不同的发展”.

参考文献：

［1］孙朝仁. 认知系统的逻辑秩序：让学习真正发生的“道”——基于数学实验的视角［J］. 江苏教育，2016（Z3）：23-26.

［2］罗增儒. 核心素养与课堂研修［J］. 中学数学教学参考，2017（23）：14-20.

［3］孙朝仁. 初中数学“教思考”的教学细化——以“分式”为例［J］. 江苏教育，2020（91）：38-40+60.

［4］丁小将. 试析微专题在中考数学复习中的应用［J］. 数学教学通讯，2021（08）：60-61

［5］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.