中考作图题考查的不仅仅是“作图”

杨国智 李英

［摘  要］ 中考作图题种类繁多，不同的作图题，其“道理”不尽相同，考查的内容和方法也不相同，这就需要学生有较强的空间观念、几何直观、数学思维能力和动手操作能力，这些题目在落实课程标准要求的基础上很好地考查了学生的数学核心素养.

［关键词］ 中考；作图题；数学核心素养

在距离中考还有两周的时候，我们进行了中考数学适应性模拟检测，其中填空题的第17小题，我们选择了2021年四川省自贡市中考数学试卷的填空题第17题. 之所以选择这道题，原因有两点：一是作图题以填空题的形式来呈现，形式比较新颖；二是题目要求只用不带刻度的直尺，在格点中作图，有别于传统的“尺规”作图. 但分析试卷发现本题的得分率低于0.5，这是为什么呢？

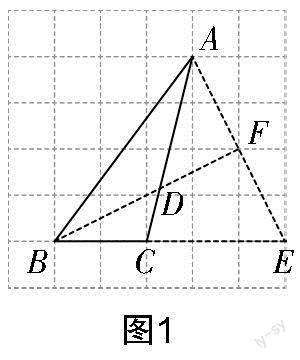
试题1  （2021年自贡中考第17题）如图1所示，△ABC的顶点均在正方形网格的格点上. 只用不带刻度的直尺，作出△ABC的角平分线BD（不写作法，保留作图痕迹）.

作法解析：延长BC到点E，使得CE为3个单位长度，连接AE，AE恰好经过格点F，作射线BF交AC于点D. BD就是△ABC的角平分线.

在网格中，根据勾股定理易知△ABC的边AB的长为5个单位长度，延长BC到点E，使得BE的长也是5个单位长度，则△ABE是等腰三角形，∠ABC是等腰三角形ABE的顶角，F是等腰三角形ABE的底边AE的中点，根据等腰三角形“三线合一”的性质可知，BF平分∠ABC.

本题考查的重点是：作图——应用——设计，涉及的知识点有勾股定理、等腰三角形的性质等，解题的关键是数学知识的迁移和转化思想的应用.

传统的尺规作图

初中数学的作图题，以尺规作图为主. 所谓尺规作图，就是在平面内使用圆规和无刻度直尺通过有限次操作完成图形与几何中的作图问题. 其中，无刻度直尺的主要功能是连接两点作线段或过两点作射线和直线；圆规的功能是用来画圆、弧，截取一条线段等于已知线段. 关于尺规作图，《义务教育数学课程标准（2022年版）》有明确要求，即能用尺规作图：作一个角等于已知角；作一个角的平分线；作一条线段的垂直平分线；过一点作已知直线的垂线； 过直线外一点作这条直线的垂线； 已知三边、两边及其夹角、两角及其夹边作三角形；已知底边及底边上的高线作等腰三角形；已知一直角边和斜边作直角三角形；过不在同一直线上的三点作圆；作三角形的外接圆、内切圆；作圆的内接正方形和正六边形；过圆外一点作圆的切线. 在尺规作图中，学生应了解作图的原理，保留作图的痕迹，不要求写出作法［1］.

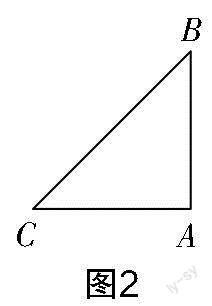
试题2  如图2所示，在Rt△ABC中，∠A=90°，AB=AC.

（1）请用尺规作图的方法在边AC上确定点D，使得点D到边BC的距离等于DA的长（保留作图痕迹，不写作法）；

（2）在（1）的条件下，求证：BC=AB+AD.

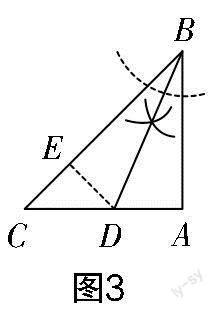
第（1）问作法解析：确定点D须满足两个条件，即一是点D必须在线段AC上；二是点D到角的两边BC和BA的距离相等. 根据“到角的两边距离相等的点在这个角的平分线上”可知，D是∠ABC的平分线与边AC的交点，所以只需要用尺规作出△ABC的内角∠ABC的平分线即可确定点D（作图如图3所示）.

传统的尺规作图，都是数学课程标准要求掌握的最基本的作图，学生只要理解作图的基本原理，就可以完成作图. 尺规作图一般要求学生作图过程用虚线表示，作图结果用实线表示.

仅利用无刻度直尺作图

仅用无刻度直尺作图，是近几年中考作图题的创新类试题，这类试题能有效地引发学生积极思考，引导学生利用观察、猜测、推理、直观想象等数学学习方法分析问题并积极地解决问题，有助于学生数学核心素养的形成.

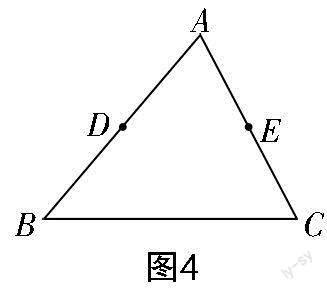
试题3  如图4所示，点D，E分别是△ABC中AB，AC边的中点，请仅用无刻度直尺按下列要求画图.

（1）在BC边上画出中点F；

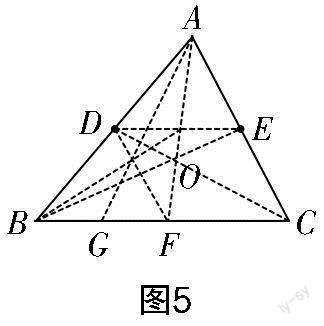
作法解析：（1）因为三角形的三条中线交于一点，已知了两个中点，第三个中点也就知道了. 连接CD，BE相交于点O，作射线AO交BC于点F. 点F就是BC边的中点. （2）所求的点G是BF的中点，在△ABF中，已知D是AB的中点，要找到边BF的中点，必须先确定边AF的中点. 在△ABC中，因为D，E分别是AB，AC的中点，所以DE是△ABC的中位线，即DE∥BC，根据平行线等分线段定理，可以确定线段AF的中点，再根据（1）的方法，点G即可确定.（作图如图5所示）

此作图题涉及的知识点有三角形的重心、三角形的中位线和平行线等分线段定理等.

图形与几何的作图题，是学生用数学语言表达实际问题情境中简单的数量关系与空间形式的重要方式，学生只有在充分理解、掌握相关知识的基础上，才能运用数学语言（几何作图）准确地表达出空间形式和数量关系. 数学语言的简洁美，能使学生逐步养成用数学语言（图形语言和符号语言）表达与交流的习惯.

利用网格格点作图

利用“网格+无刻度的直尺”完成作图，成为数学中考作图题的“新贵”. 这类试题涉及的知识点繁多，综合性较强，能够很好地考查学生运用所学知识解决实际问题的能力.

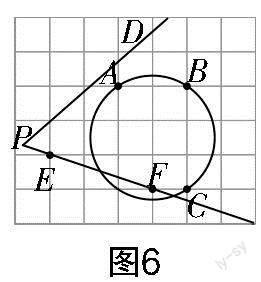
试题4  如图6所示，在每个小正方形的边长均为1的网格中，圆上的点A，B，C及∠DPF一边上的点E，F均在格点上.

（1）线段EF的长等于______；

（2）若点M，N分别在射线PD，PF上，满足∠MBN =90°，且BM = BN，请用无刻度的直尺，在网格中画出点M，N，并简要说明点M，N的位置是如何找到的（不要求证明）.

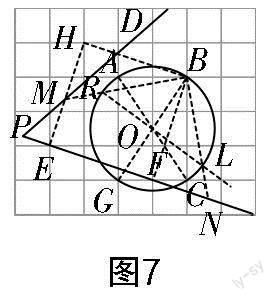
第（2）问作法解析：如图7所示，因为格点A，B，C都在圆上，所以2×3的矩形第四个頂点也在圆上，设这个点为G，连接AC，BG相交于点O，则点O为已知圆的圆心. 以线段EF为一边作正方形EHBF，EH交PD于点M，连接BM交☉O于点R，连接RO并延长，交☉O于点L，连接BL并延长，交PF于点N. 因为四边形EHBF是正方形，所以BH=BF，且∠HBF=90°，又因为RL是☉O的直径，所以∠MBN=90°，所以∠HBM=∠FBN. 易得△HBM≌△FBN，所以BM=BN.

本题涉及的知识有：90°的圆周角所对的弦是直径、正方形的判定和性质、全等三角形的判定等. 在这里，利用好线段EF是解决问题的关键，这也是本题第（1）问求线段EF长度的原因吧.

数学学习，不单单是知识的积累，更重要的是要通过具体数学情境中的基本数量关系和空间形式，能够直观地理解所学数学知识及其现实背景，能够运用所学数学知识表达事物之间的联系与规律，从而培养想象力和创新意识.

在坐标系中利用平移、旋转或轴对称作图

七至九年级的“图形与几何”领域包括“图形的性质”“图形的变化”和“图形与坐标”三个学习主题. 而利用网格或平面直角坐标系作图，是用代数的方法来研究图形的轴对称、旋转和平移变化规律，其能在用几何直观理解图形基本事实的基础上，进一步理解和掌握图形的性质和定理.

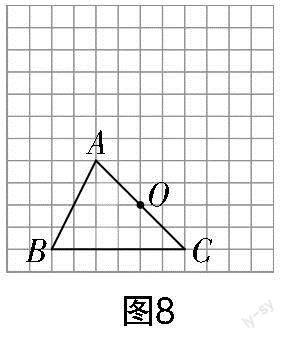
试题5  如图8所示，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点）.

（1）将△ABC先向上平移6个单位長度，再向右平移2个单位长度，得到△ABC，请画出△ABC﹔

（2）以边AC的中点O为旋转中心，将△ABC按逆时针方向旋转180°，得到△ABC，请画出△ABC.

作法解析：（1）根据平移的方式确定点A，B，C的位置，再顺次连接即可得到△ABC；

（2）根据旋转可确定点A2，B2，C2的位置，再顺次连接即可得到△ABC.

本题考查作图——旋转变换与平移变换，解题的关键是理解题意，灵活运用所学知识解决问题.

拓展延伸

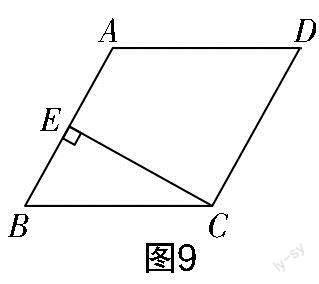
试题6  如图9所示，在菱形ABCD中，CE⊥AB，∠B=60°.

（1）请仅用无刻度的直尺完成下列画图，不写画法，保留画图痕迹.

①求作菱形ABCD中BC边上的高AF；

②求作AD的中点G.

（2）在（1）的条件下，连接EG，设AF与CE交于点H，若FH=1，求EG的长.

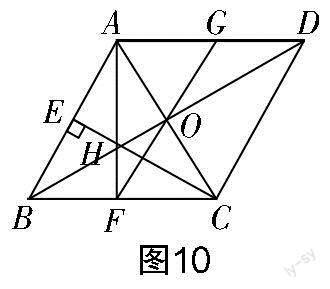
第（1）问作法解析：①连接AC，BD，相交于点O，设BD与CE相交于点H，连接AH并延长，交BC于点F，AF就是BC边上的高. 因为四边形ABCD是菱形，所以BD⊥AC，AB=AC. 又因为∠ABC=60° ，所以△ABC是等边三角形. 因为BD⊥AC，所以∠HBE=30° . 因为CE⊥AB，∠ABC=60°，所以∠HCF=30°. 所以HB=HC. 又因为AB=AC，所以AF⊥BC（到线段两个端点距离相等的点在线段的垂直平分线上）.

②连接FO并延长，交AD于点G，G就是AD的中点.

给定的作图工具越少，作图的难度越大. 本题虽然只限定用无刻度的直尺完成作图，包含的信息量不多，但考查的知识点非常多，主要有菱形的性质、等腰（等边）三角形的性质、线段垂直平分线的判定、三角形的中位线以及平行线分线段成比例，需要较强的综合能力.

作图题同图形的性质与判定有着紧密的联系，不同的作图题，其“道理”可能不尽相同，考查的内容和方法也不相同，这就需要学生有较强的空间观念、几何直观、数学思维能力和动手操作能力. 作图题在落实课程标准要求的基础上很好地考查了学生的数学核心素养，成为中考数学的必考题型. 作图时，学生需想象通过尺规作图操作后所形成的平面图形的形状，进一步理解尺规作图的基本原理、所涉及的知识点和所用到的作图方法，从而发展动手操作能力、空间观念和空间想象力，以达到培养数学核心素养的目的.

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.