多维联想 多方探究

范建兵

［摘  要］ 文章通过一道中考压轴题的深度剖析，引导师生在解题教学中关注知识融合和图形解构，多维联想寻思路，多方探究求生长.

［关键词］ 联想；突破；探究

试题呈现

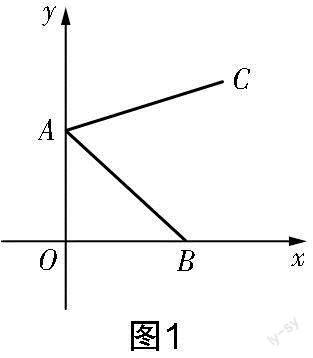
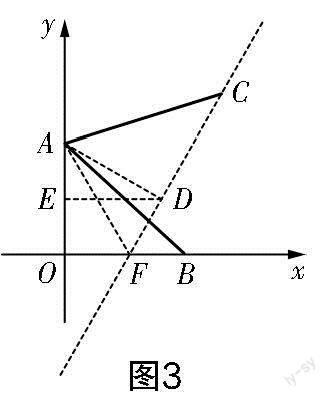
试题 （2022年江苏省苏州市中考数学卷第8题）如图1所示，点A的坐标为（0，2），点B是x轴正半轴上一点，将线段AB绕点A按逆时针方向旋转60°后得到线段AC.若点C的坐标为（m，3），则m的值为（     ）

解法探究

解题教学是数学教学中一种基本的教学方式，又是培养学生理解数学、思考数学的基本途径.本题设计巧妙，基于课本又高于课本，借助图形的旋转，融合了等边三角形、直角三角形、勾股定理、相似等几何知识，为學生提供了施展才华的广阔空间. 现提出几种解题思路，供大家参考.

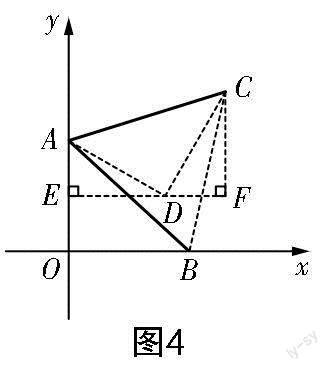
思路3 如图4所示，将线段AO绕点A按逆时针方向旋转60°后得到线段AD，过点D作DE⊥y轴，交y轴于点E，过点C作CF⊥ED，交直线ED于点F. 根据旋转可得△AED各边的长，再由“一线三直角”模型可得△AED∽△DFC，接着根据相似三角形对应边成比例且CF=2，求得DF的长，从而求出m的值.

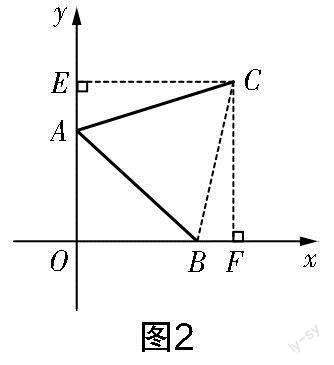
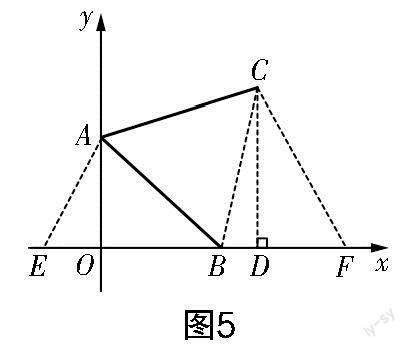
思路4 如图5所示，过点C作CD⊥x轴，交x轴于点D，连接CB，构造∠AEO=∠CFO=60°，先分别解Rt△AEO和Rt△CFD，再通过证明△AEB≌△BFC，得到AE=BF，EB=FC，从而建立方程并求得m的值.

思路5 如图6所示，与思路4相似，过点C作CE⊥y轴，交y轴于点E，连接CB，构造∠CDE=∠BFO=60°，先分别解Rt△CDE和Rt△BFO，再通过证明△CDA≌△AFB，得到CD=AF，DA=FB，从而建立方程并求得m的值.

……

试题评价

1. 思路探寻，从条件中想关联

G.波利亚在《怎样解题：数学思维的新方法》一书中提醒我们：你以前见过它吗？你是否见过形式稍有不同的类似问题？你能从已知数据中得出一些有用的东西吗？你能以不同的方式推导这个结果吗［1］ ？这说明问题的解决离不开联想，联想能够帮助我们有效地、快速地探寻到解题思路.

苏州前几年的中考几何综合题，往往涉及许多知识点，并且有着较难的图形识别要求.2022年第8题一改“常态”，以最基础、最简洁的几何图形（线段）为载体，考查了学生对几何变换（旋转）的理解. 题目看似简单，但简单图形中却蕴含了丰富的思维要求，对学生的几何直观、抽象意识、应用意识等素养要求很高. 解题时，我们不妨将试题中的各类知识串联起来，通过知识的整体性与关联性展开联想，寻找可能的解题思路. 如由“旋转”联想到变换前后的变和不变，由“60°角”联想到等边三角形和特殊角的三角函数值，由“计算边长”联想到勾股定理，由“平面直角坐标系”联想到点的对应、直线解析式、关键点的坐标、待定系数法等……

2. 方法探究，从经验中寻突破

G.波利亚将数学解题划分为四个阶段：读题、拟订方案、执行、回顾［2］. 反思以上几种思路：对于思路1，学生比较容易想到，但它对学生的运算能力要求太高，许多学生看到方程时望而却步，无法顺利求解；思路2和思路3的思考源于对旋转的深度理解，特别是在平面直角坐标系中，要求学生能将线段AB的旋转习惯性地看成是△AOB的旋转（这种思考问题的意识需要教师在平时的教学中不断渗透），找出其中的定量（点D的位置和点C的轨迹）与变量（点B和点C的坐标），这样更有利于问题的解决. 顺利读题、拟订方案、执行方案后，学生还需要养成良好的回顾与反思解题习惯，突破经验再思考：我是怎么想到的？还可以怎么想？哪种方法更好一些？

3. 模型识别，从解题中找思路

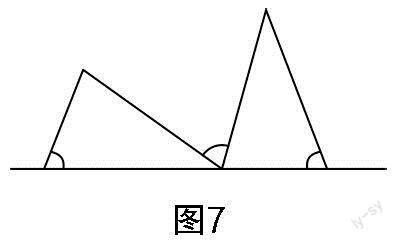
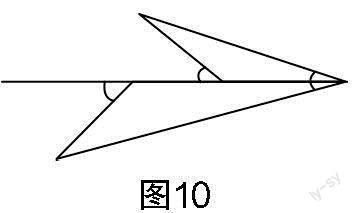
加强解题教学不是同一问题的反复训练，更不是搞题海战术. 它的正确做法是通过解题和反思活动，在解题的基础上总结、归纳解题方法，强化建模意识，提炼数学模型，提升学生素养. 思路4和思路5都应用了“一线三等角”解题模型，借助模型来构造图形的全等或相似，从而建立方程并求解. 作为一个常练常考的几何模型，“一线三等角”深受教师和学生的喜爱，在苏科版教材八年级上册第35页和九年级下册第59页、第91页都有明确的“一线三等角”图例. 教学中，教师要鼓励学生“窥一斑而知全豹”，引导学生在已有学习经验上不断关联和引申. 图7至图12都是“一线三等角”常见的基本图形（可根据角度大小与相等角的分布进行分类）. 因此，解题教学中增加基本图形的识别与构造，可以丰富学生的认知结构，完善学生的知识体系，提高学生分析问题与解决问题的能力，提升学生的模型观念，增强学生的创新意识.

4. 深度探究，在反思中求生长

深度学习是在已有认知结构上的一种完善与递进. 在问题解决的基础上，为了让学生更好地理解问题的解决路径，实现中考题引发思考和引领教学的潜在功能，我们可以通过对原有问题的再提问、再改编等方式对具体知识进行再建构，以引发师生深度理解，促进解题经验的再生长.

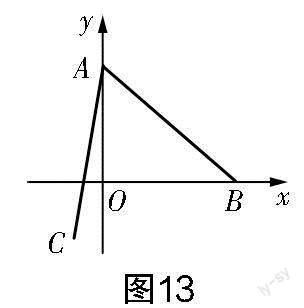
改编1 基于原题旋转方向的改编.

如图13所示，点A的坐标为（0，2），点B是x轴正半轴上的一点，将线段AB绕点A按顺时针方向旋转60°后得到线段AC.若点C的坐标为（m，-1），则m的值为____.

改编2 基于原题旋转角度的改编.

如图14所示，点A的坐标为（0，2），点B是x轴正半轴上的一点，将线段AB绕点A按逆时针方向旋转45°后得到线段AC.若点C的坐标为（m，3），则m的值为____.

改编3 基于原题隐含结论的再挖掘.

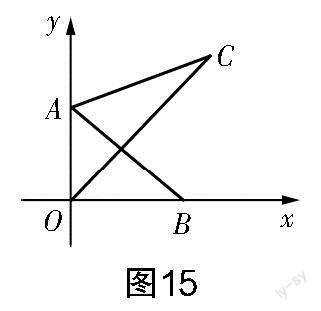
如图15所示，点A的坐标为（0，2），点B是x轴上的一个动点，将线段AB绕点A按逆时针方向旋转60°后得到线段AC，连接OC，则线段OC的最小值为____.

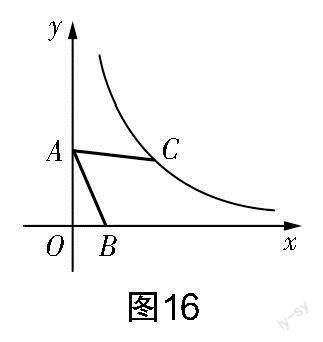
改编4 基于知识的再融合.

结束语

什么是好题？个人认为好题应该具备来路正、出路广、融合强、韵味足的特征，源于课本但又高于课本，既能够体现基本知识和基本技能的考查，又能够引领学生解题能力的提高和数学素养的提升［2］. 2022年江苏省苏州市中考数学卷第8题就是好题的代表，具有图形简洁、构造简单、思路宽广的好题之韵，让人流连忘返、回味无穷.

参考文献：

［1］G.波利亚. 怎样解题：数学思维的新方法［M］. 涂泓，冯承天，译. 上海：上海科技教育出版社，2011.

［2］陈伟华. 认清“来路”   认准“出路”——以2020年苏州市中考数学卷第18题为例［J］. 中学数学杂志，2021（10）：53-54.