合理利用思维导图 构建优质复习课堂

叶晓红

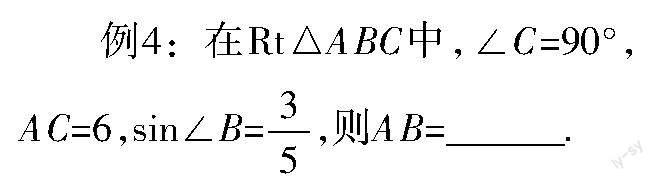
［摘  要］ 思维导图作为一种新型笔记方法，在提高教学质量、提升学习品质、發展学生学习能力等方面具有突出的价值. 在复习教学中，合理地运用思维导图可以将那些碎片化的知识串联起来，将那些“见不到、摸不着”的数学思想方法形象地展示出来，这样既有利于学生理解和掌握知识，又有利于学生提升迁移能力. 同时，思维导图可以完美地呈现知识间的内在联系，可以帮助学生把握知识的内在逻辑，能培养学生的分析能力和综合能力，并提升学生的学习品质.

［关键词］ 思维导图；迁移能力；学习品质

思维导图既是一种思维方式，又是一种学习形式，其在提升学生学习能力、发展学生数学素养等方面发挥着不可估量的作用，因此思维导图在初中复习教学中得到了广泛的应用. 在复习教学中，合理地运用思维导图可以将分散于各章节的知识点按照一定的逻辑、类别等组织起来，形成知识体系，以便于学生理解和迁移.

复习课教学的作用

复习课是数学教学的重要课型. 复习课将已学知识进行重现和再认识，从而将前后知识串联起来，形成知识网络，以此提升学生的数学综合应用能力. 不过重现不是简单的重复，若教师按部就班地将知识点一一罗列出来，然后让学生整理、记忆，之后通过大量的练习进行巩固和强化，这样“炒冷饭”式的复习模式将难以调动学生学习的积极性，不利于学生思维能力的提高.

在复习课教学中，教师需要完成以下两个任务：一是将碎片化的知识系统化，让学生在头脑中形成清晰的知识脉络；二是使抽象化的思维直观化，将抽象的数学思维形象地表达出来，便于学生理解和记忆. 思维导图为完成以上两个任务带来了便利，为此它自然成了提升复习课堂效率的重要工具.

思维导图在复习课教学中的应用

笔者教学“解直角三角形”复习课时，运用思维导图帮助学生进行知识和方法的梳理，获得了很好的教学效果，现将教学过程分享给大家，供参考！

1. 碎片化的知识系统化

数学学习活动应该是具有一定方向性，且能调动学生积极参与、主动建构的学习过程，它应该是生动活泼的，富有个性的. 在复习课教学中，教师要尽量减少或避免知识的罗列，要为学生提供一个主动思考和合作学习的机会，让学生通过思考、交流去探究知识间的联系，从而将碎片化的知识进行整理，使之系统化，这样既能让学生巩固已有知识、经验和方法，又能为新知的理解和掌握做铺垫，有助于学生提升学习能力. 为了避免知识罗列所带来的枯燥感，在复习教学设计中，教师不妨设计一些有针对性的小题，以题带动知识点的复习，以此调动学生参与的积极性，从而在巩固知识的基础上，提高学生的数学应用能力.

在本课例教学中，为了让学生能够主动建构求边长问题的知识体系，教师设计了一些前置小问题，让学生通过思考和交流进行信息的提取与加工，以形成知识体系.

（1）教学设计

【环节1：习题设计】

例1：在Rt△ABC中，∠C=90°，AC=6，BC=8，则AB=______.

例2：如图1所示，在Rt△ABC中，∠C=90°，AC=6，BC=8，点D在BC上，且AD=BD，则AD=______.

例3：如图2所示，在Rt△ABC中，∠C=90°，AC=6，∠B=30°，则BC=______.

【环节2：问题设计】

问题1：以上四道例题，你会解吗？

问题2：以上例题有何异同点？

问题3：你能尝试利用思维导图将以上例题按照不同解法进行归类吗？

【环节3：活动设计】

活动1：让学生独立完成以上4道例题的求解. （时间：大约3分钟）

教师巡视学生的解题过程，发现学生解题中存在的问题.

活动2：交流展示学生的解题过程. （时间：大约3分钟）

以上例题难度较小，为此在该环节教师应重点展示学困生的解题过程，通过学困生所展示出的问题进行针对性引导，从而让每个学生都能有所提升.

活动3：组内交流问题2和问题3. （时间：大约2分钟）

活动4：展示小组合作成果. （时间：大约2分钟）

在小组展示成果过程中，教师鼓励其他小组进行质疑和补充，由此将小组合作变为班内合作，丰富学生的认知.

（2）教学片段

师：现在给大家2分钟的时间，画出以上四道例题不同解法的思维导图. （4个学生为一个小组）

师：请各小组派代表展示一下你们的研究成果.

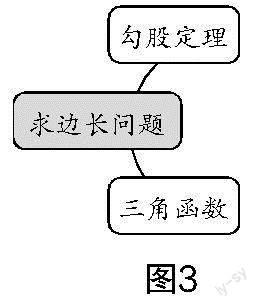
生1：我们小组是这样画的. （学生边说边在黑板上绘制，得到了如图3所示的思维导图）

师：对于生1小组得到的研究成果，你们是否有需要补充的？

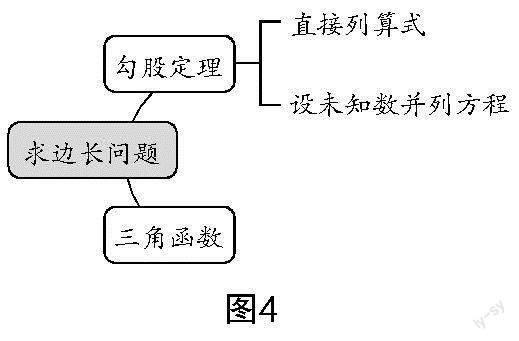
生2：我们认为这个分类还不够完整. 对于例1和例2，虽然这两道题都是利用勾股定理来求解的，但是例1可以直接列算式计算，而例2需要设未知数、列方程，所以在此基础上，我们小组做了一些补充，得到图4. （该生在原有的思维导图上进行补充）

师：很好，还有其他要补充的吗？

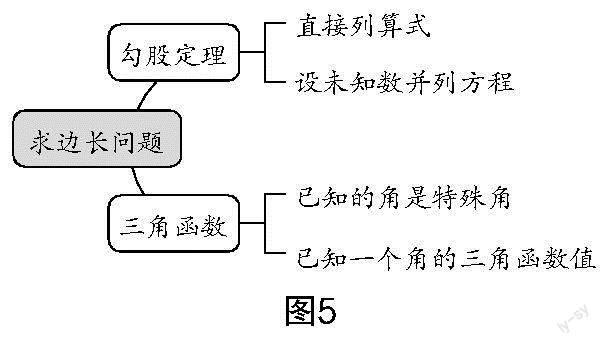
生3：对于例3和例4，虽然解题时都用了三角函数，但是在方法上有所区别，一个给出的是特殊角，另一个给出的是一个角的三角函数值，所以可以做如下补充. （生3进一步补充得到了图5）

师：回忆以前所学的知识，对于求边长问题，除了应用以上方法外，是否还有其他方法呢？

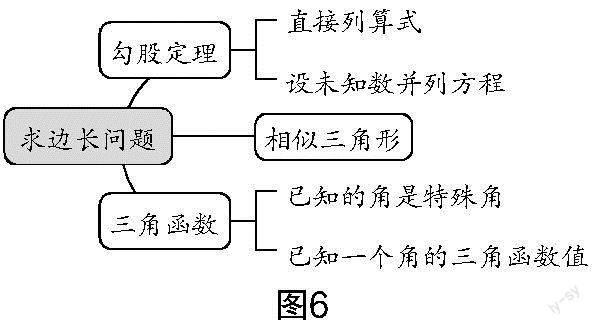
生4：利用相似三角形求边长.

师：哦！对的，看来是老师考虑不周了，题目中并未体现，生4补充得非常好. （教师补充完善思维导图，如图6所示）

（3）教学思考

教学时，教师借助一些小试题引导学生进行独立思考和合作交流，总结、归纳出了求边长问题的常用解决方法. 从师生互动和生生互动交流的过程来看，大多数学生所掌握的知识依然比较碎片化，虽然他们给出了思维导图，不过思维导图的建立依赖于解题，个体完善的认知体系并未建立. 而生4跳出了原有题目的束缚，提出了解决边长问题的常用方法——相似三角形，这说明他对求边长问题有着宏观和整体的把握. 其实，在实际教学中教师经常发现，很多学生在解题时常常是想到哪里就算到哪里，缺乏整体和全局意识，究其原因就是学生掌握的知识比较碎片化，所以在解题时常常因难以找到最优解决方法而影响解题效果. 而思维导图的运用，可以将这些碎片化的知识整合起来，形成一个完善的思维链，将问题的解决策略系统化地呈现，以此提高解题效率.

2. 抽象化的思维直观化

谈起数学，很多人都会用“抽象”来概括，抽象是數学的本质，它给数学学习增加了阻力. 而思维导图可以鲜明地将知识间的关系直观地、系统地呈现出来，从而使抽象的数学知识变得更加直观化、系统化，便于学生理解和接受. 思维导图的运用，很好地呈现了数学知识的内在逻辑，使得学生头脑中存储的信息呈现出放射状和网格化，为知识的迁移奠定了坚实的基础.

在以上教学环节中，学生通过思考与合作，利用思维导图呈现了求边长问题的基本方法，为了让学生更直观地感受数学知识，教师进一步拓展延伸，以期通过具体应用拓展学生的认知，丰富学生的解题经验，提高学生的解题效率.

（1）探究与应用

【环节1：习题设计】

例5：如图7所示，在观测站O正东方向4 km处有一港口A，某船从港口A出发，沿北偏东15°方向航行到B处，此时从观测站O观测到该船位于北偏东60°方向，求该船行驶的距离.

【环节2：活动设计】

活动1：预留2分钟让学生独立思考，寻找解决问题的思路.

活动2：在教师的引导下，展示学生的思维过程.

（2）教学片段

师：对于例5，解题前我们需要明确什么内容？

生（齐）：已知是什么，要求什么.

师：很好. 结合图7，谁来说一说我们要求什么.

生5：求斜三角形OAB中AB的长.

师：很好，也就是解决斜三角形的边长问题. （教师板书关键词：斜三角形求边长问题）

师：现在我们一起探索一下解决此类问题首先需要做什么.

生（齐）：找已知. （思维导图分支一：一找）

师：很好，根据已知找关于这个斜三角形的三个条件，思考一下，对于这三个条件，有没有特殊的要求呢？

生6：这三个条件中必须有一个为边. （拓展分支一：三个条件（有一边），如图8所示）

师：说得很好，根据已知容易找到一边OA=4，那么其他两个条件是什么呢？

生7：根据已知条件，我发现∠BOA=30°，∠OAB=105°.

师：很好，这样我们又找到了两角，现在凑齐了三个条件，接下来我们怎么办呢？

生8：作高，构建直角三角形. （思维导图分支二：二作）

师：那么过哪个顶点作高呢？三个顶点都可以吗？

生9：应该是过点A作高. 在△OAB中，∠BOA=30°，∠B=45°，这两个角都是特殊角，所以在作高时需要保留这两个特殊角. 故应该过点A作高. 若过其他两点作高，将破坏特殊角，不利于求解.

师：回答得太棒了！作高时一定要注意，不能破坏特殊角. （完善分支二：不能破坏特殊角，如图9所示）

师：通过以上分析，我们作好了高，接下来做什么呢？

生（齐）：列式计算. （教师完善思维导图，如图10所示）

上述过程通过一步步探究，帮助学生完善了解斜三角形边长问题的思维导图. 思维导图形成后，教师让学生按照此思路重新认识例5，共同完成了该题的解答过程.

师：思考一下，对于例6，我们应该如何求解. （教师用PPT给出例6）

例6：如图11所示，在一条笔直的海岸线l上有A，B两个观测站，A观测站在B观测站的正东方2 km处. 现有一艘小船在点P处，从A站处测得小船在北偏西60°方向，从B站处测得小船在北偏东45°方向. 小船继续沿AP方向行驶至C处. 此时，从B站处测得小船在北偏西15°方向，求C处到B站的距离.

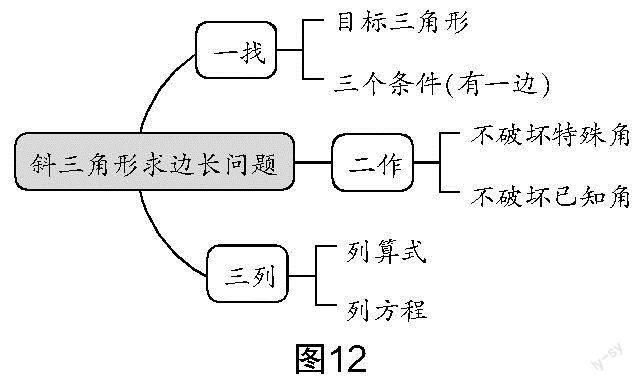
教师引导学生将例6与例5进行类比，在原有基础上进一步完善思维导图，如图12所示. 学生形成思维导图后，教师预留时间让学生独立完成该例6的解答.

（3）教学思考

数学知识是抽象且复杂的，若学生在学习中不重视方法，只死记硬背，将难以理解和记忆知识，这样很容易出现“懂而不会，会而不对”的现象. 数学知识是相互关联的，若在学习过程中学生不能从整体和全局的角度去认识知识，不能建构知识网络，那么学生将难以形成深刻的记忆. 此外，随着学习内容的不断增多，需要记忆的内容也越来越多，此时学生若不能找到合适的方法有效存取信息，很容易造成思维混乱，从而影响解题效率. 基于此，在复习教学中，教师需要引导学生进行知识的梳理，避免杂乱无章地任意堆放，要使知识变得有序、系统. 特别地，教师要充分发挥其示范功能，展现教师的思维过程，让学生也能像教师那样思考问题. 若想达到以上教学效果，教师在解题教学中可以引导学生利用思维导图，从而将知识、方法向系统化、直观化转化. 如在本课例教学中，在探究与应用阶段，教师通过“低起点、小坡度”的问题引导学生总结、归纳了解斜三角形边长问题的一般方法，并将其用思维导图直观地呈现了出来，完成了知识的系统化建构，这有利于学生快速形成解题策略，从而提高解题效率.

教学体会

从以上教学过程中不难发现，学生的思路不再完全地跟着教师走，学生可以提出自己的疑问，展现自己的思维过程，建构个体完善的思维导图，学生可以更加直观地感受知识，深刻地理解知识. 对教师而言，为学生提供自由开放的空间，引导学生思考、探索、建构，会在调动学生主观能动性的同时，为课堂增加许多不可控因素，这会给教师的“教”带来一定的挑战. 因此，教师要认真地研究教材，研究学生，做好精心预设，从而有的放矢地应对各种课堂生成，提高教学有效性.

在学习过程中，应用思维导图，可以使思维变得更加有序. 在建构思维导图的过程中，教师要打破以师为主的教学模式，要充分发挥小组互助、互相启迪的作用，鼓励学生呈现自己的思维过程，从而建构一个完善的认知体系，让不同的学生都能获得不同的成长. 如，在本课例教学过程中，教师引导学生自主建构思维导图，然后通过不断的交流进行补充和调整，充分地调动了学生的参与积极性，优化了学生的认知，使学生形成了系统的解题策略，提升了学习品质.

总之，在复习教学中，教师不要急于灌输和讲解，应该为学生提供一个自由的、开放的学习空间，充分利用好思维导图的优势，以此提高学生的数据分析、数学抽象、归纳推理等能力和素养.