注重推理过程,提升推理能力
2023-11-15潘敬贞钱耀周
潘敬贞 钱耀周










[摘 要] 立体几何是发展学生直观想象和逻辑推理素养的重要载体,也是每年高考必考的内容.文章从考查思路、求解思路和解法评析等方面对2023年全国新高考Ⅰ卷“立体几何解答题”进行分析,提出几点教学建议与大家交流、探讨.
[关键词] 立体几何;试题分析;逻辑推理;教学思考
逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的方法. 推理形式有归纳推理、类比推理和演绎推理.逻辑推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质[1].立体几何是发展学生直观想象和逻辑推理素养的重要载体,也是每年高考必考的内容. 立体几何解答题的第(1)题一般是证明平行或垂直的问题,求解这类问题先直观感知点、线、面的位置关系,然后根据相关的几何性质、定理和推理规则进行证明. 论证过程要环环相扣,一步一步地推进,每一步都有理有据,语言表述要准确精练,符合推理规则.
然而很多学生证明立体几何中的平行与垂直时,却表现出:逻辑思维混乱,说理过程不连贯,缺乏论据;语言表述啰唆,不精炼,不准确. 本文从考查思路、求解思路和解法评析等方面对2023年全国新高考Ⅰ卷“立体几何解答题”进行分析,提出几点教学建议与大家交流、探讨.
试题呈现与分析
1. 试题呈现
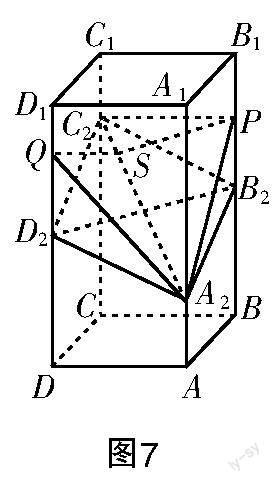
(2023年全国新高考Ⅰ卷第18题)如图1所示,在正四棱柱ABCD-ABCD中,AB=2,AA=4.点A,B,C,D分别在棱AA,BB,CC,DD上,AA=1,BB=DD=2,CC=3.
(1)证明:BC∥AD;
(2)点P在棱BB上,当二面角P-AC-D为150°时,求BP.
2. 试题分析
本题以正四棱柱为载体,第(1)题证明线线平行,第(2)题通过二面角的大小来确定动点P的位置并求线段BP的长度. 试题背景熟悉,问法常见. 试题难度不大,但有一定的灵活性和综合性,而且具有良好的信度和区分度. 试题主要考查正四棱柱的概念与性质、面面平行的性质、平行四边形的性质、线线平行的性质、二面角的定义、向量法等基本知识,以及直观想象、逻辑推理与数学运算等素养.
求解思路分析
第(1)题的求解思路比较多,为学生解决问题提供了广阔的思维空间. 可以结合正四棱柱的性质证明线线平行,也可以结合面面平行的性质定理证明线线平行;可以先构造平行四边形,再利用线线平行的传递性证明结论成立;还可以利用向量法进行证明. 第(2)题先设动点P的坐标,再求两个平面的法向量,利用向量的夹角公式列方程,最后解方程获解. 第(2)题还可以用几何法求解,但求解过程比较复杂.
1. 解答第(1)题
(1)思路1(向量)
评析 由于第(2)题可以用向量法求解,因此第(1)题可依题意建立空间直角坐标系用坐标法求解. 解法1的思路自然,过程简洁,效率高,是一种不错的解法;解法2是求解本题的通法.这两种解法简单好用,但有不少学生漏掉了“A,B,C,D四点不共线”这一重要步骤,使得说理不够充分,逻辑推理不够严密. 另外,大部分学生证明线线平行时习惯用几何法,这向教师提示:在平时教学中,要引导学生从多角度思考问题,并比较各种方法的优缺点.
(2)思路2(平行四边形)
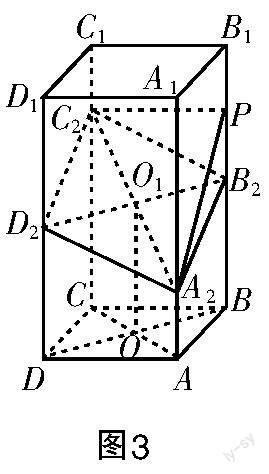
解法1(平行四边形的性质) 如图3所示,连接AC,BD,设AC∩BD=O,取AC的中点O,连接OO. 因为ABCD是正方形,所以O是AC的中点.由题设条件可知OO是梯形AACC的中位线,所以OO=2.又DD=BB=OO=2,DD∥CC//BB∥OO,所以D,O,B三点共线,即A,B,C,D四点共面. 又O是BD的中点,所以O是BD的中点,所以ABCD是平行四边形,所以BC∥AD.
评析 解法1先证四点共面,再证对角线相互平分,最后根据平行四边形的性质证明对边平行. 然而不少学生由于各种原因漏掉了四点共面的证明,导致结论不成立(对角线相互平分有可能是空间四边形).解法1对数学综合能力的要求比较高,一般学生很难做到:条理要清晰,说理要充分,推理要严密.
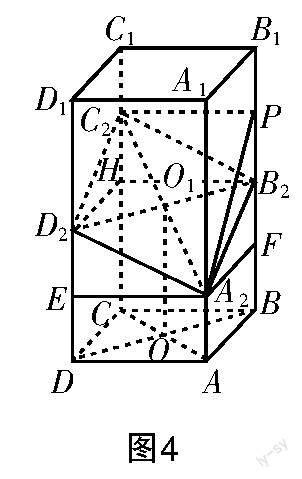
解法2(棱形概念) 如图4所示,连接AC,BD,设AC∩BD=O,取AC的中点O,连接OO. 因为ABCD是正方形,所以O是AC的中点. 由题设条件可知OO是梯形AACC的中位线,所以OO=2.又DD=BB=OO=2,DD∥CC∥BB∥OO,所以D,O,B三点共线,所以A,B,C,D四点共面. 作AE⊥DD,垂足为E;作AF⊥BB,垂足为F. 取CC的中点H,连接DH,BH,则DH⊥CC,BH⊥CC. 在直角三角形中利用勾股定理易得AD=AB=
评析 不少学生求出四边形ABCD的边长后发现四条边相等就认定其是菱形,漏掉了四点共面的证明,自然结论不成立.
(3)思路3
评析 解法1与解法2的思路基本一致,求解思路虽然清晰,但涉及的知识面比较广泛,不仅要用到平面向量基本定理,还要用到面面平行的性质定理. 在表述过程中,不少学生漏掉了“平面AADD∩平面ABCD=AD,平面BBCC∩平面ABCD=BC”,使得推理不严密,說理不充分,结论站不住脚.
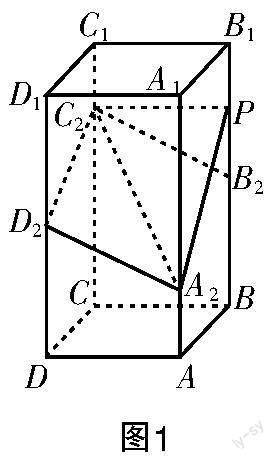
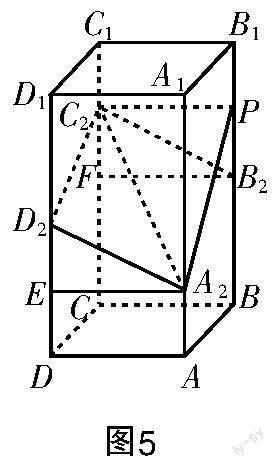
解法3(全等+面面平行) 如图5所示,作AE⊥DD,垂足为E;作BF⊥CC,垂足为F. 由题设条件可得DE=CF,∠DEA=∠CFB,AE=BF,所以△AED≌△BFC,所以∠EAD=∠FBC. 因为平面AADD∥平面BBCC,且=,=,所以BC∥AD.
评析 解法3先证明两个三角形全等得到两个角相等,然后根据空间等角定理得到结论. 不少学生的求解思路与解法3基本一致,但推理过程漏洞百出,有的没指出面面平行,有的没指出角的两边方向相同,这样推理得到的结论是不成立的,很容易举出反例.
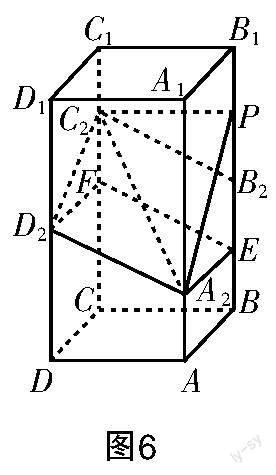
(4)思路4(线线平行的传递性)
如图6所示,分别设线段BB,CC的中点为E,F,连接EF,AE,DF,由题设条件可得BE=CF,BE∥CF,所以四边形BCFE是平行四边形,所以BC∥EF. 因为AE∥AB∥CD∥DF,且AE=AB=CD=DF,所以四边形AEFD是平行四边形,所以AD∥EF. 所以BC∥AD.
评析 思路4符合大部分学生的思维习惯,解答过程简洁,也容易表述,解答效率高.思路4可以说是第(1)题最优的几何法.
2. 解答第(2)题
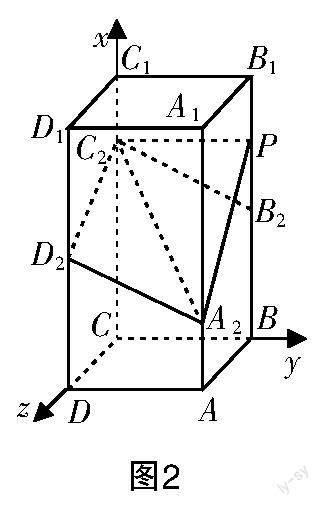
(1)思路1(解析法)
评析 解法2根据二面角的定义,先在两个半平面内分别作交线的垂线,然后用向量法解决两条异面直线的夹角问题. 解法2接地气,解答过程简洁,效率高,是不错的解法,但很少有学生能想到该解法,这需要教师在平时教学中引导学生思考,积累这方面的解题经验.
(2)思路2(几何法)
作PS⊥AC于S,连接QS,则QS⊥
评析 该解法具有一定的靈活性,关键是掌握并运用正四棱柱的性质转化问题,需要学生具备完整的逻辑链条以及较强的运算求解和推理论证能力,一般的学生很难想到该解法,利用该解法并顺利解决问题的学生就更少. (几何法)还可以在两个半平面分别作交线的垂线,再平移垂线使其相交于一点,然后连线得三角形,求出三角形的边长(用参数表示出来),由余弦定理列出关于参数的方程,最后求出参数的值即可得BP的值. 但该解法方程较多、字母较多,求解过程繁杂,效率不高. 相对而言,向量法(解析法)的求解过程更简洁,效率更高,凸显了向量法(解析法)的优越性.
教学建议
1. 提出新的问题——培育深度思考
2. 加强技能训练——实现熟能生巧
数学学习离不开必要的技能训练[2],选择不同的几何体(圆锥、棱锥、圆柱、棱柱、圆台、棱台)为载体,设置不同的证明路径为问题情境,让学生运用不同的几何知识证明不同的问题,深化知识的理解,构建知识体系.在证明平行的问题中,设置三角形的中位线、平行四边形、相似三角形、线面平行的性质定理、面面平行的性质定理等证明路径为问题情境;在证明垂直的问题中,设置线面垂直的性质定理、菱形的对角线、等腰三角形“三线合一”、面面垂直的性质定理、圆周角是直角等证明路径为问题情境. 在推理证明训练中培养学生的说理能力、推理能力,实现推理过程熟能生巧;鼓励学生多角度思考问题、解决问题,让学生体会问题的本质,培养学生的发散思维和理性精神.
3. 重视推理过程——提升推理能力
立体几何是培育学生逻辑推理能力的好素材,立体几何证明问题的求解教学切不可“蜻蜓点水”走过场,更不能停留在知识表层机械式操作,没有上升到数学概念内部的思维演绎层面,没有直击核心素养内核的重复练习是无益的,要让学生真实参与推理证明过程,体验思维发展过程,彰显推理论证的学习价值.因此,在立体几何证明问题的求解教学中,教师要重视推理过程,要循序渐进地开展教学,先引领学生弄清推理的依据是什么、推理的规则是什么、推理的目标是什么,然后带领学生一步一步地推理,讨论每一步推理的充分性与必要性,逐渐提升推理能力,形成推理素养.
4. 注重数学表达——培育理性思维
图形是从实物和模型抽象后的产物,也是形象、直观的语言;文字是对图形的描述、解释与讨论;符号则是对文字语言的简化. 因此,教学立体几何时要重视几何语言表达的训练与培育,要特别注意“模型→图形→文字→符号”这一抽象过程[3]. 求解问题时,要引导学生用数学思维思考问题,用数学语言表述问题,表达过程要注意语言的连贯性与准确性. 在训练与规范数学表达的过程中培育学生的理性思维,提升学生的思维品质.
参考文献:
[1] 中华人民共和国教育部. 普通高中数学课程标准(2017年版)[M]. 北京:人民教育出版社,2017.
[2] 李刚. 在问题探究中构建知识的整体关联——以“圆锥曲线中一类定点定值问题”为例[J]. 数学通报,2023,62(02):16-21.
[3] 李海东. 基于核心素养的“立体几何初步”教材设计与教学思考[J]. 数学教育学报,2019,28(01):8-11.
