周边固支效应靶薄板冲击响应的稳健性分析
2023-11-06翟红波李尚青毛伯永苏健军
翟红波,李尚青,毛伯永,丁 刚,苏健军
(西安近代化学研究所 西安,710065)
引言
冲击波超压是装药爆炸的主要效应之一,相关测试方法受到诸多关注[1-3]。压电式压力传感器电测法是应用最广泛的方法,其采用压电材料作为传感器敏感部件,将冲击波压力信号转换为电信号,基于压电晶体压电效应解算出压力的时间历程曲线,具有准确性高、信息全的优点;但其布设较为复杂,耗时长,爆炸近区生存性差,难以适应大规模移动式的工程测试。效应靶测试法利用冲击波加载条件下金属薄板的塑性变形量,定量表征冲击波的特征参数,装配简单,布设方便,是压电式压力传感器电测法的有益补充。
近年来,爆炸冲击波作用下金属薄板塑性变形方面的研究较多,并取得了一些有价值的研究成果。李旭东等[4]分析了爆炸与均布载荷耦合加载下固支钢板的破坏效应。傅辉刚等[5]通过有限元模拟方法,建立了薄板变形挠度、爆心距以及TNT 当量之间的关联关系,探讨了冲击波能量谱、薄板自振频率对薄板变形的影响规律。姬建荣等[6]通过激波管试验,建立了某型圆形铝板的最大挠度、激波峰值之间的关系。李丽萍等[7]在靶场试验的基础上,建立了薄板变形与交会条件的量纲分析模型,通过炸高参量的引入考虑了冲击波入射角度对薄板变形的影响,该模型经过试验验证,对于一定范围内的冲击波压力测量工程问题具有良好的指导作用。张显丕等[8]将效应靶拓展应用于装药水下近场爆炸测试,基于能量吸收比例系数,提出了无量纲化的威力损伤因子,建立了不同规格靶板的变形等效关系。这些效应靶塑性变形的研究都为效应靶的压力测量工程应用打下了基础。
效应靶的敏感元件为金属薄板,其几何尺寸、材料参数及外载荷等存在随机性,导致薄板变形值出现随机性,进而影响压力测量的准确性。关于金属薄板变形稳健性的研究较少,且多局限在静态载荷、装配工艺[9]等方面。灵敏度分析是随机研究的重要方法,已广泛应用于很多领域[10-12]。笔者基于效应靶圆板的冲击响应理论计算方法,结合Monte-Carlo数值模拟的可靠性灵敏度分析方法,分析了主要因素对周边固支效应靶薄板变形稳健性及其灵敏度的影响,有助于明晰效应靶设计的主控参量,为压力效应靶的设计与应用提供参考。
1 冲击波作用下周边固支效应靶薄板的变形计算方法
1.1 周边固支效应靶薄板的力学模型
某5 孔式压力效应靶如图1 所示,由基座、中间体、响应膜片、盖板、引压孔、压紧螺栓孔及压紧螺栓等构成,响应膜片通过中间体与盖板的紧固连接而固定。当外界冲击波作用到效应靶时,首先通过盖板上的引压孔,然后作用到响应膜片上。引压孔具有一定的倒角,以抑制稀疏波的产生,降低其对压力效应靶变形的干扰。

图1 某5 孔式压力效应靶Fig.1 A circular effect target with five hole
图2 为圆形薄板结构的简化力学模型。在冲击波压力的作用下,响应膜片发生弯曲变形(方向与载荷作用方向一致),膜片上部由于压缩为压应力区,膜片下部由于拉伸为拉应力区。当拉压应力超过材料的屈服极限时,响应膜片发生塑性变形;当拉压应力超过材料的极限强度时,效应靶断裂。若冲击波波阵面法线与效应靶膜片表面垂直,即正入射情况,则压力效应靶的最大挠度出现在膜片几何中心处,此时最大挠度值主要取决于冲击波超压峰值及冲量,可采用最大挠度表征爆炸冲击波压力,将该效应靶作为压力测量工具来使用。
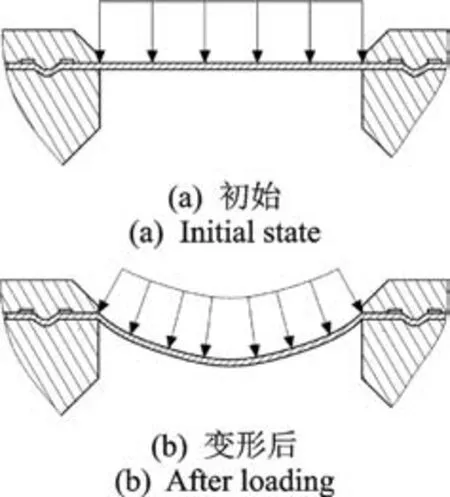
图2 圆形薄板结构的简化力学模型Fig.2 The simplified mechanics mode of circular sheet structure
通过压紧螺栓,将圆形薄板固定于中间体与盖板之间,形成圆形薄板的周边固支边界。
1.2 薄板在冲击波作用下的变形计算方法
薄板在冲击波作用下的响应分析,采用如下假设:
1)薄板响应挠度远大于薄板厚度,因此只考虑膜力,不考虑弯矩对变形的影响[13];
2)薄板周边为理想的固支约束,忽略螺钉紧固、表面平整度等导致的结合部间隙问题;
3)薄板所受载荷为均布载荷,忽略冲击波压力载荷的时空不均匀性[14];
4)薄板为理想弹塑性结构。
因此,效应靶金属薄板在爆炸冲击波作用下的响应方程[15]可以表示为
其中:A为效应靶圆形薄板面积;P(t)为作用在薄板表面的均布冲击波压力;t为时刻;ρ为薄板材料密度;h为薄板厚度;ω为薄板位移响应;为薄板变形速度;为薄板变形加速度;Nr和Nθ分别为薄板径向和周向的膜力;分别为薄板径向和周向的曲率。
假设薄板变形满足Von Mises 屈服理论,圆形薄板的膜力为
其中:σd为材料的动态屈服应力。
式(1)中左边积分表示外加冲击压力和惯性力的功率,右边第1 个积分表示在任意塑性铰处耗散的能量,第2 个积分表示在任何连续变形场中耗散的能量。对于四周固支圆薄板结构,其沿边界的位移响应ω=0,则右边第1 项为0。
考虑均布冲击波压力作用,则薄板任意位置处的位移响应可表示为
其中:W为薄板中心位置的位移响应;r为离薄板中心位置的距离;R为薄板半径;α为薄板变形轮廓参数,其取值与材料有关,当材料为纯铝时,α取值为3。
按峰值不变、冲量相等的原则,将冲击波压力载荷简化为等效三角形载荷[16-17],即
其中:P0为冲击波压力峰值;τ为冲击荷载持续正压作用时间;Te为薄板停止运动的时刻。
根据载荷历程,可将薄板结构的响应分为两个阶段。将式(4)、式(5)代入式(1),并经过一系列整理,可得到周边固支效应靶薄板在冲击波压力作用下的中心点变形挠度
1.3 变形计算方法的试验验证
为验证该中心点变形计算方法,开展相关爆炸试验。装药为1 000 kg 某炸药,近地爆炸,爆炸场地面平坦。在距爆心30 m 处,布设压力效应靶,效应靶结构见图1。效应靶布设时,敏感面与地面平齐,同时在相邻位置布设内置电路压电式压力传感器。压力效应靶与压力传感器的爆心距相同,用于测量压力效应靶上的冲击波压力载荷。图3 为静爆试验冲击波压力测试布场图,左侧2 个圆面中心安装了电测压力传感器,右侧为压力效应靶,两者与爆心的距离一致。

图3 静爆试验冲击波压力测试布场图Fig.3 Shockwave test layout diagram of the static explosion
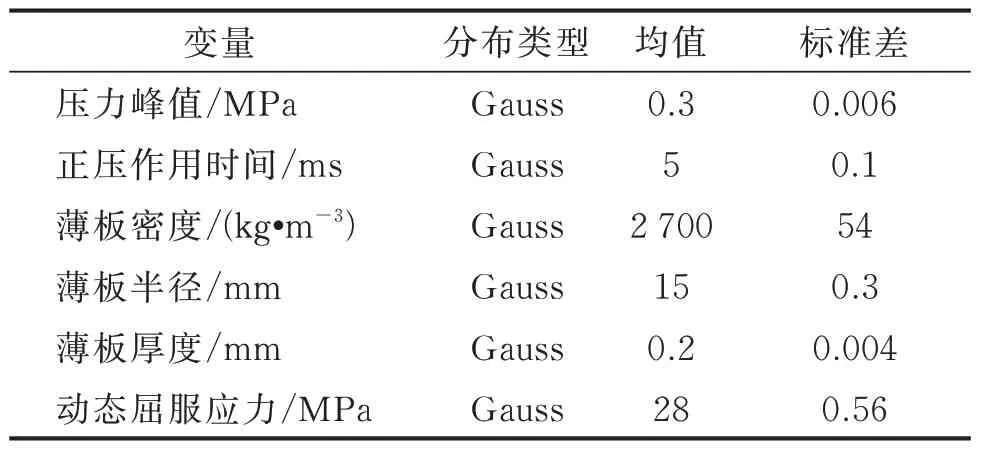
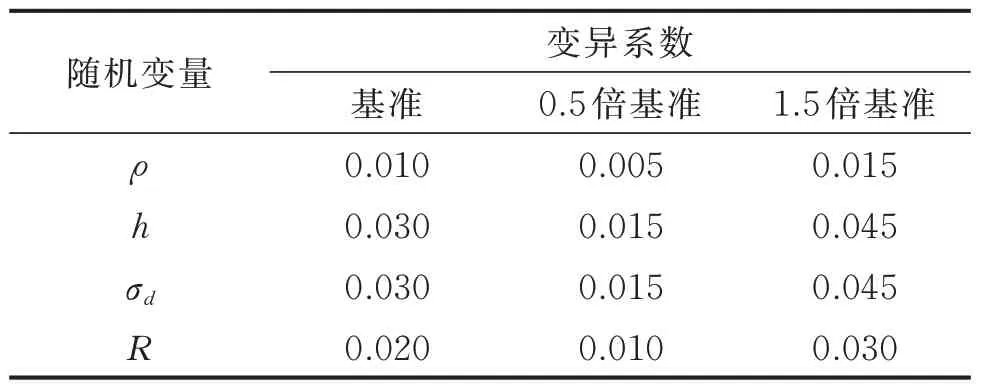
试验中,采用压力传感器测得的该处冲击波压力峰值为0.234 MPa,正压作用时间为8.454 ms,冲量为986 Pa•s。将其简化为三角波载荷曲线,峰值为0.234 MPa,正压作用时间约为4.002 ms。效应靶薄板所用材料为延展性较好的1060 铝,其动态屈服应力为28 MPa,密度为2 700 kg/m3,膜片直径为30 mm,厚度为0.2 mm。基于该简化载荷,分别采用式(6)与有限元仿真方法,得到不同方法的薄板中心点挠度对比,如表1 所示。

表1 不同方法得到的薄板中心点挠度对比Tab.1 Comparison of center point deflection results with different means
由表1 可知,该中心点变形挠度计算模型所得结果与试验值相对偏差为5.97%,相比仿真结果的偏差稍大。这主要是由于该响应模型未考虑弯矩和冲击波载荷不均匀性的影响,但该结果依然小于爆炸场冲击波压力动态测量的不确定度12%,在可接受范围内。
2 变形稳健性表征方法
压力效应靶通过薄板中心点挠度获取爆炸冲击波压力,所以其变形的稳健性非常重要。效应靶薄板在爆炸作用下的响应过程较为复杂,受到薄板尺寸、材料参数以及冲击波形等因素的影响。这些因素具有一定的随机性,导致薄板变形也会出现随机性,从而影响压力效应靶的测量精度。
为降低这种随机性的影响,应将薄板变形控制在一定范围内。假定某条件下薄板中心点挠度为Wf,随机参数条件下中心点挠度为W,最大允许偏差为k。当1-k 其中:x为随机参数的向量。 在数学上,薄板中心变形的稳健性指标可表示为 其中:θx为随机变量x的分布参数;fx为x的联合分布概率密度函数。 式(8)的非线性程度较高,采用Monte-Carlo 法进行分析,计算结果最为精确。极限状态函数z(x)为基本随机变量x={x1,x2,…,xn}T的函数,有效域定义为Ω={x:z(x)<0},式(8)可以转化为[18] 其中:Rn为n维变量空间;IΩ(x)为有效域的指示函数。 IΩ(x)可表示为 薄板变形稳健性的灵敏度可通过对分布参数θi求导得到,即 假设各随机变量xi(i=1,2,…,n)均服从正态分布且相互独立,分布参数为μi和σ2i,则式(12)右端的可表示为 式(12)右端为总体均值,此时用Monte Carlo 法抽取的样本均值代替,就能够得到变形稳健性对各影响因素分布参数的灵敏度。为了便于对比分析,还需将灵敏度值做相对标准化处理[19] 采用图1 所示的压力效应靶,压力载荷峰值取0.3 MPa,正压作用时间取5 ms,输入变量的随机分布类型及参数如表2 所示。最大允许偏差k设为0.1,即薄板变形值偏离10%以内是可接受的。 表2 输入变量的随机分布类型及参数Tab.2 Distribution patterns and parameters of input variables 采用Monte Carlo 法计算该工况的变形稳健性,模拟次数从1 000 次到100 万次。变形稳健性和抽样次数的关系如图4 所示。可以发现,在抽样次数为30 万次以下时,变形稳健性的计算结果波动较大;随着抽样次数的增加,计算结果趋于稳定。这说明薄板变形稳健性分析的非线性较强,需要很大的样本量。为保证计算精度,后面计算的抽样次数均采用100 万次。 图4 变形稳健性和抽样次数的关系Fig.4 The curves of deformation robustness and sampling times 不同质量装药爆炸时,产生的冲击波波形结构不同。为分析压力效应靶在不同爆炸工况下的适用性,计算该型薄板在不同波形压力作用下的变形稳健性。所有输入变量均服从正态分布。薄板密度为2 700 kg/m3,变异系数为0.01;薄板半径为15 mm,变异系数为0.02;薄板厚度为0.2 mm,变异系数为0.03;动态屈服应力为28 MPa,变异系数为0.03。压力峰值与正压作用时间的变异系数取0.001。图5 所示为变形稳健性和正压作用时间的关系,可以发现,随着正压作用时间的变化,变形稳健性基本不变,说明在正压作用时间1~10 ms 范围内,薄板变形稳健性结果趋于一致。 图5 变形稳健性和正压作用时间的关系Fig.5 The curves of deformation robustness and positive pressure action time 爆炸冲击波压力峰值可按萨道夫斯基公式计算[20],即 其中:m为装药的TNT 当量;s为距装药中心的距离。 爆炸冲击波比冲量可按式(17)计算[21] 其中:C为与炸药性能有关的系数,对于TNT,可取196~245。 联合式(16)与式(17),可以得到压力峰值为0.3 MPa、比冲量为300~3 000 Pa•s 对应的装药质量约为80~80 000 kg,涵盖了中大型爆炸装药质量。说明该型效应靶能够用于多种爆炸工况,适用范围较广。 针对不同的测试工况,设计了多种规格薄板的效应靶。分析4 种典型薄板的变形稳健性,如表3 所示。所有输入变量均服从正态分布,薄板半径变异系数取0.02,厚度变异系数取0.03;压力峰值为0.03 MPa,正压作用时间为3 ms,二者变异系数为0.001;薄板密度和动态屈服应力的取值与图5 的算例相同。由表3 可知:薄板1,2,3 的厚度相同,半径梯次增大,而稳健性逐渐降低,说明薄板厚度相同时其变形稳健性随半径厚度比增大而降低;薄板4 的半径是薄板1 的10 倍,但二者的半径厚度比相同,薄板4的变形稳健性显著小于薄板1,说明半径厚度比相同时薄板变形稳健性随厚度的增大而降低。这是由于薄板冲击变形与半径的4 次方基本呈正比,与薄板厚度呈反比,当半径厚度比增大时,半径对变形值的影响急剧增加,进而导致变形值的变异系数增加,稳健性下降。因此,设计效应靶时,应在允许范围内缩小薄板半径,增大薄板厚度,以此增加其变形稳健性,有助于提高测试精度。 表3 4 种典型薄板的变形稳健性Tab.3 Deformation robustness of four typical thin plates 以表3 中的薄板1 为研究对象,参数取值与其相同。为简化研究,将压力峰值、正压作用时间作为确定量。薄板的材料密度ρ、厚度h、动态屈服应力σd以及半径R仍为随机变量,服从正态分布且相互独立,薄板的3 组变异系数如表4 所示。 表4 薄板的3 组变异系数Tab.4 Three sets of coefficient of variation of the thin plates 计算3 种变异系数下薄板变形稳健性对4 种变量的灵敏度,其中:μρ为ρ的均值,σρ为ρ的标准差;μh为h的均值,σh为h的标准差;μσd为σd的均值,σσd为σd的标准差;μR为R的均值,σR为R的标准差。不同变异系数下薄板变形稳健性灵敏度计算结果和饼图分别如表5 和图6 所示。可以发现,各变量的灵敏度随着变异系数的增大而增大,其中薄板半径标准差σR的灵敏度最大,是变形稳健性的主控参量。因此,在效应靶设计加工中,应重点控制薄板半径的一致性,减小半径的标准差,以提高薄板变形的稳健性。 表5 不同变异系数下薄板变形稳健性灵敏度计算结果Tab.5 The robustness sensitivity with different coefficient of variation 图6 不同变异系数下稳健性灵敏度饼图Fig.6 The pie chart of robustness sensitivity with different coefficient of variation 结合周边固支效应靶薄板的冲击响应理论与基于Monte-Carlo 数值模拟的可靠性灵敏度分析方法,提出一种周边固支效应靶薄板变形稳健性表征方法,分析了主要因素对变形稳健性及其灵敏度的影响规律。结果表明,薄板变形稳健性随半径厚度比、厚度的增大而降低;薄板半径标准差的灵敏度最大,是薄板变形稳健性的主控参量。所得结果为周边固支效应靶的设计与压力测量分析提供了参考。3 稳健性灵敏度分析
4 结果与讨论
4.1 抽样次数的影响

4.2 各变量对稳健性的影响


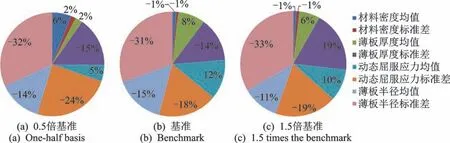
4.3 各变量对稳健性灵敏度的影响

5 结束语
