考虑层间变形的约束阻尼圆柱壳振动特性分析∗

马宏伟，陈中石，孙 伟

（1.东北大学机械工程与自动化学院 沈阳，110819）（2.东北大学航空动力装备振动及控制教育部重点实验室 沈阳，110819）

引言

圆柱壳结构由于比强度、比刚度高，在航空、航天及舰船等装备中有着广泛的应用。其在机械、气动及热等载荷作用下，很容易引发过大的振动而导致结构本身或者整个装备的性能失效。众多减振方法中，在圆柱壳结构的表面贴敷约束阻尼层（通常为局部贴敷）是一种最经济、最有效的方法［1，2］。

针对圆柱壳结构进行局部贴敷约束阻尼层减振，首先要创建可以预测复合壳结构振动特性的动力学分析模型。当前，相关研究方法主要包括解析法（或者半解析法）和有限元法。Chen 等［3］利用薄壳理论和唐奈尔-穆斯塔里-弗拉索夫（Donnell-Mushtari -Vlasov，简称DMV）的假设推导了局部贴敷约束阻尼圆柱壳结构的一般运动微分方程，分析了贴敷厚度对复合圆柱壳振动特性的影响，这是一种典型的半解析法。基于DMV 假设和拉格朗日方程，Zheng 等［4］推导了局部贴敷约束阻尼层圆柱壳结构的动力学方程，分析了不同贴敷方案的约束阻尼层圆柱壳结构振动特性。基于线弹性薄壳理论，向宇等［5］推导了局部贴敷约束阻尼层圆柱壳的一阶常微分方程，并分析了贴敷位置对复合壳振动特性的影响。基于Donnell′s 假设和线性黏弹性理论，Zheng 等［6］构造了被动约束层阻尼圆柱壳的本构关系，利用哈密顿原理导出了约束层阻尼处理圆柱壳的运动方程。损耗因子是表征贴敷阻尼材料结构损耗能量的重要指标，张安付等［7］提供了一种多种阻尼处理下圆柱壳损耗参数的解析换算方法。

相对于解析或者半解析法，有限元法具有更广泛的适用性。Wang 等［8］利用有限元法将局部贴敷约束阻尼层圆柱壳等效为单层后，进行了振动和阻尼分析，并讨论了材料性能、厚度、处理区域和位置等参数对复合壳振动特性的影响。Masti 等［9］基于有限元法和一阶剪切变形理论，建立了一种4 节点80 自由度的复合壳单元，用于分析局部贴敷约束阻尼层圆柱壳结构的振动特性，并与实验对比验证了模型的正确性。经过约束阻尼层处理的圆柱壳部分主要由基体层、黏弹性层和约束层构成，其主要减振原理是在圆柱壳振动时，黏弹性层因基体层和约束层的交错变形出现剪切效应，导致消耗更多的能量，所以在复合圆柱壳动力学建模过程中，需要考虑这种层间的变形关系。基于层间变形关系和改进的波传递法，Gao 等［10］采用瑞利-里兹法求解了贴敷约束阻尼层圆柱壳的自由振动问题。基于半解析法，Song 等［11］在考虑层间变形的基础上，推导了约束阻尼层圆柱壳在任意边界条件下的动力学方程。基于薄壳理论，Mokhtari 等［12］在考虑层间变形关系下，利用拉格朗日能量方程和瑞丽-里兹法求解了复合圆柱壳的动力学方程，并分析了厚度和半径等参数对结构振动特性的影响。利用层间变形关系和经典薄壳理论，Jin 等［13］采用傅里叶级数作为容许函数，推导了约束阻尼圆柱壳的动力学方程，并讨论了不同层厚和剪切参数对其振动特性的影响。上述考虑层间变形关系的约束阻尼层圆柱壳动力学建模均属于解析或者半解析法，如果这种层间变形关系没有引入到有限元建模分析中，将导致有限元分析结果与实际结果存在偏差。

对于局部贴敷约束阻尼层的圆柱壳结构，既存在包含3 层结构的复合壳单元，也存在仅包含基体的单层壳单元。在有限元法建模中，如何将这种不同类型的单元组集在一起，实现正确的单元组集非常重要。笔者采用有限元法对局部贴敷约束阻尼层圆柱壳结构进行了动力学建模方法研究。在建模中考虑了层间变形关系，推导了复合单元的刚度及质量矩阵，构造了一种过渡单元来实现局部贴敷约束阻尼层圆柱壳总刚度及总质量矩阵的有效组集。

1 考虑层间关系复合圆柱壳单元推导

本研究的局部贴敷约束阻尼层圆柱壳模型如图1 所示，底部为弹性约束，并在自由端贴敷约束阻尼层。其中：R为复合圆柱壳的等效半径；L为圆柱壳总高度；L1为约束阻尼层贴敷的宽度；hs，hv和hc分别为基体、黏弹性层和约束层厚度。在圆柱壳中心建立柱坐标系（x，θ，z），对应的复合圆柱壳的等效中性面上局部位移用u，v和w来表示。

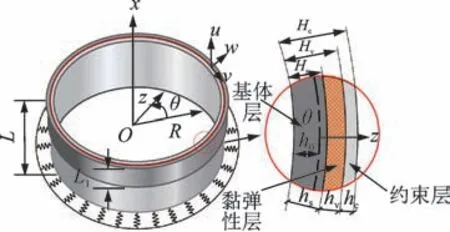
图1 局部贴敷约束阻尼层圆柱壳模型Fig.1 Cylindrical shell model with partially attached constrained damping layer

其中：E(k)，Hk分别为第k层材料的弹性模量和上表面到圆柱壳内表面的距离，且H0=0；k=1，2，3 分别表示基体层、黏弹性层和约束层

1.1 层间变形关系

基于Donnell's 薄壳理论，复合圆柱壳中基体层和约束层内任意一点位移场可表示为

约束阻尼层圆柱壳层间变形如图2 所示，假设复合结构基体层和约束层中性面分别由A-A'处沿周向变形了vs和vc，变形至B-B'处。这时，通过B-B'处的C-C'和D-D'层面可以看出，各层间位移变化是协调连续的［11］。

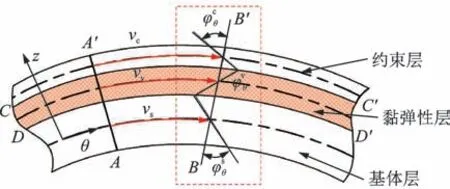
图2 约束阻尼层圆柱壳层间变形示意图Fig.2 Diagram of interlayer deformation of cylindrical shells with constrained damping layers

以周向变形为例，黏弹性层的位移uv和vv及转角位移可表示为

1.2 复合单元推导

复合圆柱壳单元如图3 所示，其中Rs，Rv和Rc分别为基体、黏弹性层和约束层的几何中面半径。

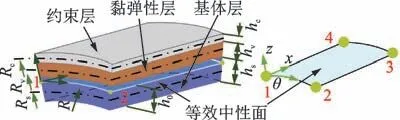
图3 复合圆柱壳单元Fig.3 Shell element of composite cylindrical shell

该复合壳单元包含4 个节点，设每个节点具有15 个自由度，任一节点位移qi为

其中：i=1，2，3，4。

由层间关系描述可知，黏弹性层的位移变形可由基体层和约束层的位移变形来表达。在单元推导过程中，可以先确定基体层、约束层的位移和应变等，再引入层间变形关系确定黏弹性层的上述参数。

可以假定任意方向位移，例如z方向位移w在曲面坐标x和θ方向上的位移场为

其中：a1，a2，…，a12为多项式系数。

复合壳单元等效中性面上任意一点的位移场为

其中：Ni为节点i=1，2，3，4 对应的形函数。

为方便构造黏弹性层的形函数，式（7）中形函数Ni也可改写为

式（8）对应基体及约束层的形函数。将式（6）代入描述层间变形关系的式（3）中，并进行相应的整理，得到黏弹性层的形函数。

复合壳单元某层任意一点应变与位移的关系为

整理可得复合壳单元各层中性面应变-位移关系为

其中：L 为矩阵微分算子；各层形函数Ns=；qe为单元节点位移向量；Bk为第k层应变矩阵。

黏弹性层的剪切应变为

同理可得黏弹性层的剪切应变-位移关系为

黏弹性层在x和θ方向的剪切应力可表示为

其中：χ为剪切修正因子，一般取。

由广义胡克定律，得到复合圆柱壳与基体及约束层相关的力与弯矩为

其中：Dk为第k层弹性矩阵。

黏弹性层所受的剪力为

因此，可得各层单元刚度和质量矩阵表达式为

其中：ρk为各层材料的密度；“∗”表示矩阵为复矩阵。

复合壳单元的刚度矩阵和质量矩阵为

上面推导了考虑层间变形关系下的复合壳单元的单元矩阵，而对于不考虑变形关系建模时，可假设为3 层均满足Donnell's 薄壳理论，并令单元节点位移自由度为

这里黏弹性层的变形不再由基体层和约束层所表征，所以不再单独考虑式（11）中黏弹性层剪切变形。各层的单元刚度矩阵和质量矩阵可表示为

2 基体单元和过渡单元推导

对于局部贴敷约束阻尼层圆柱壳结构，除包含贴敷约束阻尼层区域外还包含未贴敷区域。由于未贴敷区域的基体单元不包含约束层自由度，假如均利用复合单元进行组集，会出现总刚度矩阵奇异而无法求解的情况，故需要分开考虑这2 种单元。另外，由于有限元模型中贴敷区的复合单元和未贴敷区的基体单元的自由度不一致，直接将这2 种单元进行组集同样存在困难。因此，本研究在贴敷区和未贴敷区之间构造了一种过渡单元来连接复合单元和基体单元，形成如图4 所示的局部结构单元分布。

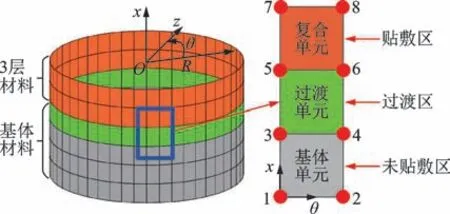
图4 局部结构单元分布Fig.4 Element distribution of local structure

2.1 基体单元构造

图4 中的未贴敷区只含有基体层，首先将复合壳单元中黏弹性层和约束层的参数设为0，得到矩阵，其维度为60×60。由于单矩阵格式较大，这里只列出单元内的第1 号节点的矩阵形式

2.2 过渡单元构造

图4 中的过渡区也仅包含基体层，但此处的单元要同时与约束阻尼层单元和基体单元相连接。为确保相容性，在构造过渡单元时，需要保证5 号和6 号节点与约束阻尼单元节点自由度一致（每个节点15 个自由度），3 号和4 号节点与基体自由度一致（每个节点9 个自由度），这样过渡单元各节点就存在不同的自由度。

3 有限元方程的建立及求解

3.1 弹性边界条件的模拟

本研究的局部贴敷约束阻尼层圆柱壳的一侧是通过螺栓固定在夹具上，因而圆柱壳受到的是一种弹性约束。参照文献［15］，可将底部设置多个周向连续分布的弹簧组来模拟该弹性边界条件，周向连续非均匀分布弹性约束圆柱壳模型如图5 所示，弹簧组对应的弹簧刚度分别为kx，kθ，kw，kux和kwθ。

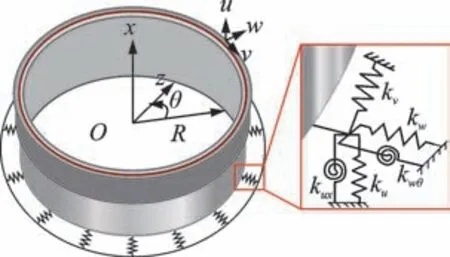
图5 周向连续非均匀分布弹性约束圆柱壳模型Fig.5 Cylindrical shell model with circumferential continuous nonuniform distribution of elastic constraints

螺栓约束本质上是非均匀的，为模拟圆柱壳底部实际周向的非均匀性，假设连续分布的各弹簧刚度满足余弦函数分布，即

其中：spr表示各边界弹簧的方向；Kspr为弹簧单元刚度值的幅度；m为底部螺栓个数；ς为螺栓影响区分布因子。

Kx，Kux，Kθ，Kw，Kwθ和ς可通过实验结果并基于分解的多目标进化算法（multi objective evolutionary algorithm based on decomposition，简称MOEA/D）进行反推辨识得到。

3.2 有限元分析

将复合圆柱壳单元、基体单元、过渡单元以及模拟弹性边界的弹簧单元组合在一起，可形成局部贴敷约束阻尼层圆柱壳的自由振动频域方程为

其中：K*为复合圆柱壳整体复刚度矩阵；Kspr为边界弹簧刚度矩阵；M为整体质量矩阵；X∗为特征向量；ω为自由振动角频率。

4 实 例

4.1 问题描述

这里以局部贴敷约束阻尼层圆柱壳为例验证本研究有限元建模方法。图6 为自由端贴敷约束阻尼层圆柱壳结构，其基体层中性面直径为450 mm，高度为210 mm，约束阻尼层贴敷在圆柱壳自由端，其高度为总高度的1/3，底部由18 个M12 规格的螺栓将圆柱壳固定在夹具上。复合圆柱壳各层材料参数如表1 所示。

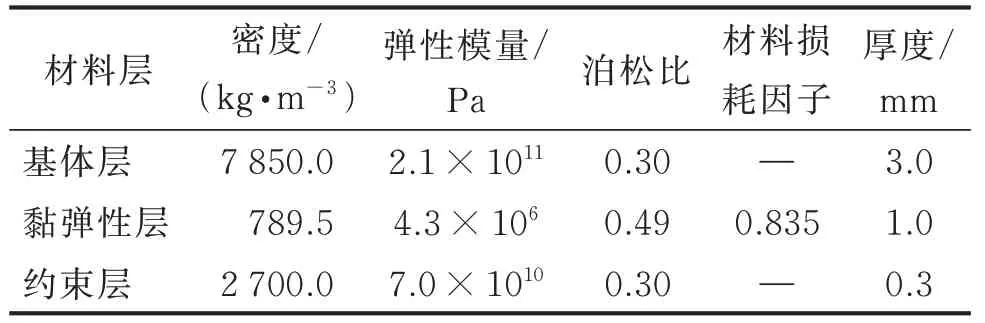
表1 复合圆柱壳各层材料参数Tab.1 Material parameters of each layer of composite cylindrical shell

图6 自由端贴敷约束阻尼层圆柱壳结构Fig.6 Cylindrical shell structure with constrained damping layer attached on free end

对复合圆柱壳的振动进行测试，测试结果用于校验所提的有限元模型。贴敷后圆柱壳锤击实验测试系统如图7 所示。采用PCB 模态力锤对复合壳进行激励，Polytec PDV-100 激光测振仪对图示激光位置进行拾振，LMS SCSDAS 便携式数据采集前端用于获取激励和响应信号，基于测试获得的频响函数反推辨识出光壳的边界条件，贴敷前后应确保边界条件不发生改变。

图7 贴敷后圆柱壳锤击实验测试系统Fig.7 Test system for hammering test of cylindrical shell after attached

4.2 模型验证

分别使用ANSYS 工程有限元分析软件及上述实验来验证考虑层间变形关系的复合壳有限元分析程序的合理性。选用Solid186 实体单元对局部贴敷约束阻尼层复合圆柱壳进行建模，共划分7 392个单元，包含40 100 个节点。自编程序共划分了288 个单元，包含336 个节点。针对2 种模型，圆柱壳底部均采用完全固定的约束，ANSYS 仿真模型如图8 所示。固支状态下复合圆柱壳前5 阶固有频率如表2 所示，其中fan和ffi分别为ANSYS 和自编程序获得的固有频率。

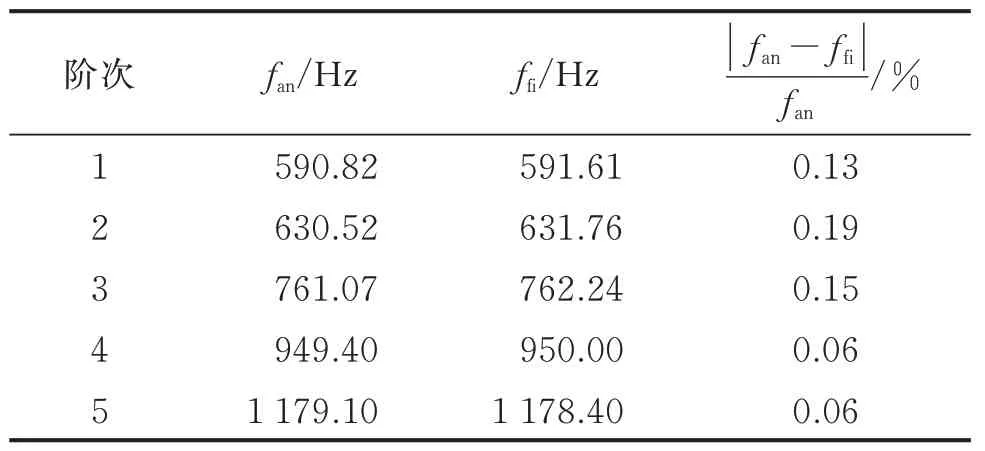
表2 固支状态下复合圆柱壳前5 阶固有频率Tab.2 The first five natural frequencies of a composite cylindrical shell under clamped conditions

图8 ANSYS 仿真模型图Fig.8 ANSYS simulation model diagram

由表2 可以看出：基于这2 种模型计算的固有频率结果较一致，前5 阶固有频率最大偏差为0.19%，但自编程序的单元数远小于ANSYS 创建模型的单元数；在求解系统固有频率方面，自编程序运算时间为36.325 s，ANSYS 仿真模型运算时间为61.3 s。由此可见，所研发的程序可显著提升该类复合壳结构动力学计算的效率。

采用实验结果进一步验证含有弹性边界约束时的自编有限元程序的合理性。通过实验测得光壳前5阶固有频率，利用MOEA/D 算法反推辨识出用于模拟弹性约束的弹簧刚度值和分布因子，如表3 所示。

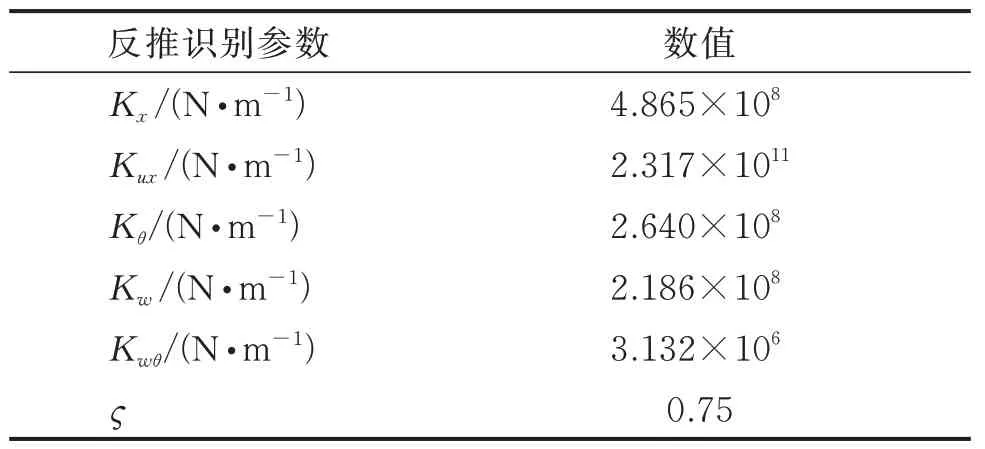
表3 模拟弹性约束的弹簧刚度值和分布因子Tab.3 Simulation elastic restraint spring stiffness values and distribution factors

将表3 中的弹簧单元参数及分布因子代入到考虑弹性边界的贴敷约束阻尼层圆柱壳有限元分析程序中，复合圆柱壳前5 阶固有频率及与实验的对比如表4 所示，实验与理论计算获得的前5 阶模态振型对比如表5 所示。表4 中列出了2 种自编有限元分析结果，其中：fign和fctd分别为不考虑及考虑层间变形关系时计算获得的复合圆柱壳固有频率；fexp为实验测得的固有频率；为相应计算结果与实测值之间的偏差。

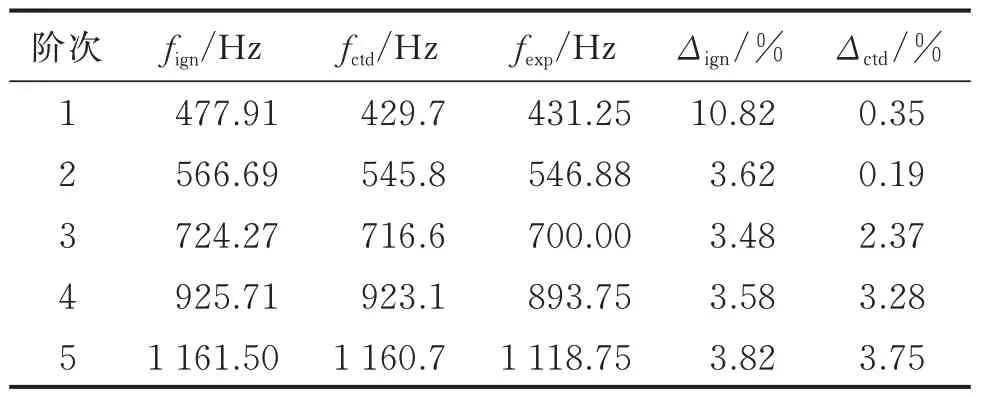
表4 弹性边界复合圆柱壳前5阶固有频率及与实验的对比Tab.4 The first five natural frequencies of composite cylindrical shells with elastic boundaries and comparison with experiments

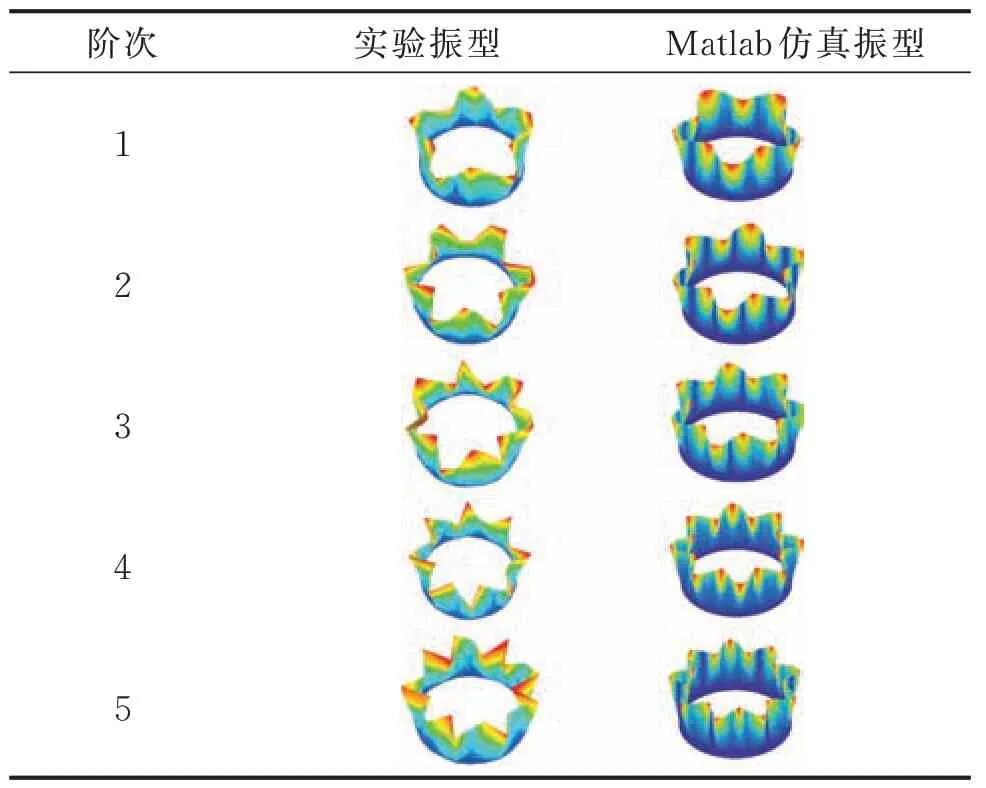
表5 实验与理论计算获得的前5 阶模态振型对比Tab.5 Comparison of the first 5 modes obtained by experiment and theoretical calculation

由表4，5 可知，采用本研究提出的考虑层间变形关系编制的有限元程序计算获得的固有频率与实验最大偏差为3.75%，计算获得的模态振型与实测基本一致，进一步证明了所研发的有限元程序的合理性。另外，从考虑及不考虑这种层间变形关系的分析结果对比来看，在约束阻尼复合壳动力学分析中，考虑层间变形关系得到的结果明显更接近实验结果，因而在实际分析时不应该忽略约束阻尼复合结构中黏弹性层的剪切变形。

4.3 参数影响分析

4.3.1 约束层厚度的影响

在仅改变分析模型约束层厚度的前提下，进行振动与阻尼分析。定义约束层与基体的厚度比，并取0.5，0.8，1.0 和1.5 这4 个值，固有频率和模态损耗因子随约束层厚度变化如图9 所示。由图可知：随着约束层厚度hc的增加，复合壳的固有频率在低阶（1～2 阶）有微小波动，而在高价（3～5阶）表现出随着约束层的厚度增加而变大的趋势；损耗因子随着约束层厚度hc的增加，在低阶（1～2 阶）逐渐增大，在高阶（3～5 阶）则出现随着约束层的厚度增加先增大再减小的现象，即产生阈值效应。因此，并不是约束层越厚越有利于减振，这可能是由于较大的约束层阻尼厚度刚度较大，反而削弱了黏弹性层剪切变形。

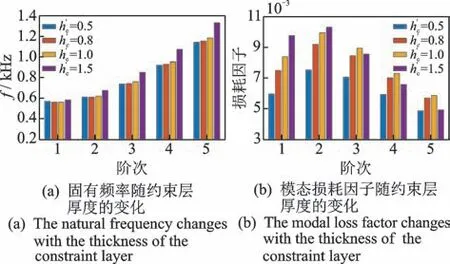
图9 固有频率和模态损耗因子随约束层厚度变化Fig.9 The natural frequency and modal loss factor vary with the thickness of the constrained layer

4.3.2 黏弹性层厚度的影响

不改变其他参数，仅改变模型的黏弹性层厚度，进行复合壳的振动与阻尼计算。定义黏弹性层与基体的厚度比为，并取0.5，0.8，1.0 和1.5 这4 个值，固有频率和模态损耗因子随黏弹性层厚度变化如图10 所示。由图可知：随着黏弹性层厚度hv的增加，固有频率值略有减少，说明黏弹性层厚度对固有频率影响不大；损耗因子各阶次均表现波动式增加，即当h'v等于0.5 和0.8 时，损耗因子变动不明显，仅当厚度比h'v的变化梯度变大时，损耗因子才有明显增加。可见，黏弹性阻尼层厚度只有达到较厚时，厚度增加才对减振有利，否则影响并不明显。

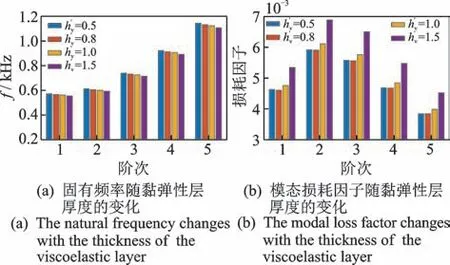
图10 固有频率和模态损耗因子随黏弹性层厚度变化Fig.10 The natural frequency and modal loss factor vary with the thickness of the viscoelastic layer

5 结论

1）针对局部贴敷约束阻尼圆柱壳，构造了一种4 节点60 自由度的复合壳单元，并进行了复合圆柱壳振动特性求解。计算结果分别与ANSYS 和实验相比较，前5 阶固有频率值最大偏差分别为0.19%和3.75%，验证了所提出有限元模型的合理性，可以在划分较少单元的前提下获得较高的精度。

2）为适应局部贴敷约束阻尼层圆柱壳结构有限元建模的需要，构造了过渡单元来连接复合壳单元和仅有基体的单层单元，实现了局部贴敷约束阻尼层圆柱壳总刚度及总质量矩阵的有效组集。该过渡单元是在不改变节点个数的前提下进行了自由度的缩减，实践表明，该过渡单元可以很好地解决不同单元类型之间的连接问题。

3）在约束阻尼复合壳动力学分析中，考虑层间变形关系得到的结果与实验结果的接近程度明显好于不考虑的情况，因此在实际分析时不应该忽略约束阻尼复合结构中黏弹性层的剪切变形。

4）分析了约束层、黏弹性层厚度变化对局部贴敷约束阻尼圆柱壳结构振动特性的影响，结果表明：约束层达到一定厚度后，复合壳固有频率会随着厚度的增加而增大，部分模态损耗因子会随着厚度的增大而减小；黏弹性层厚度对固有频率影响不大，仅当厚度达到一定程度，才会出现随着厚度的增加模态损耗因子显著增大的现象。