复合材料层板OFDR 分布式光纤冲击判位方法研究∗

2023-11-06钟照振李艳芬白瑜芳黄继伟

振动、测试与诊断 2023年5期

钟照振，曾捷，李艳芬，白瑜芳，黄继伟，綦磊

（1.南京航空航天大学机械结构力学及控制国家重点实验室南京，210016）（2.北京强度环境研究所北京，100076）（3.北京卫星环境工程研究所北京，100094）

引言

复合材料结构具有比强度大、耐疲劳性能和耐久性好等特点，已被广泛应用于航空航天领域［1］。航空航天器在服役过程中易受诸如鸟撞、空间碎片以及弹击等外物冲击［2］，特别是一些能量较小的低速冲击，虽然在物体表面未留下痕迹，但会导致复合材料结构内部出现微裂纹、分层以及纤维断裂等目视不可检损伤，这将导致其抗拉、抗压强度等力学性能下降［3］。因此，开展针对复合材料层板结构的冲击载荷位置辨识方法研究，对于保障飞行安全、提升维护检修效率具有重要意义。

目前，国内外常用于冲击载荷位置辨识的传感器主要涉及压电传感器和光纤光栅传感器。其中，压电传感器具有灵敏度高、响应快速等优点，但其需要配置大量信号传输线缆，易受电磁干扰，因此在航空航天器在轨/在役结构健康监测领域受到一定限制。光纤传感器具有抗电磁干扰、高绝缘强度、体积小、质量轻以及集信号传感与传输于一体等优点，便于构建分布式传感网络。芦吉云［4］利用小波包对碳纤维增强聚合物复合材料夹层结构的布拉格光栅传感器（fiber Bragg grating，简称FBG）冲击响应信号进行特征提取，并采用支持向量机（support vector machine，简称SVM）对冲击载荷实现定位。Pratik等［5］提出采用100 kHz 高速FBG 解调仪监测冲击信号，结合样本数据库实现冲击定位。上述2 类方法均需事先采集大量冲击响应样本数据，不仅工作量大，还会影响被测结构力学性能甚至造成预先损伤。

光频域反射型（optical frequency domain reflectometry，简称OFDR）光纤传感器采用波长横扫干涉仪测量背向瑞利散射，能够连续监测光纤沿线应变响应信息。目前，OFDR 光纤传感器广泛应用于航空航天器结构健康监测领域。Murayama 等［6］利用OFDR技术对两个不同结构粘贴胶层的内部不均匀应力进行了测量。Ciminello等［7］采用分布式光纤传感器来记录复材加筋板受冲击下的应变，监测结构的冲击损伤。

笔者采用OFDR 光纤传感器获取复合材料层板结构应变响应信息，并在此基础上提出一种基于应变幅值非线性加权原理的冲击载荷判位方法，该方法无需训练样本，具有较好的工程适用性。

1 OFDR 分布式光纤传感原理

1.1 相干探测原理

OFDR 传感基本原理主要基于相干探测技术［8］，其光路探测结构由信号光、参考光、光耦合器、混频信号、光电探测器以及拍频信号等部分组成，相干探测技术原理如图1 所示。

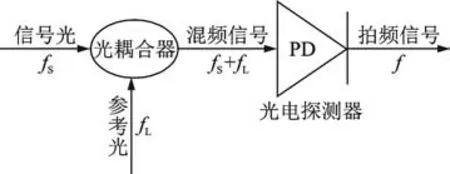
图1 相干探测技术原理Fig.1 Schematic of coherent detection technology

在相干探测系统中，信号光和参考光经光耦合器后变为混频信号，混频信号经光电探测器后转化为拍频信号，其中拍频信号的频率代表了信号光和参考光的频率之差［8］。

假设信号光与参考光的光场［8］分别为

其中：ωS，ωL分别为信号光与参考光的频率；ES，EL分别为信号光与参考光的光强。

在线性扫频情况下，拍频信号频率差的大小正比于参考光与信号光的时延τz，而拍频信号的幅度正比于测试光信号强度。因此，根据拍频信号的幅频特性，可以实现对于待测光纤上特征传感点的定位。

假设z为传感点位置，则位置计算公式［8］为

其中：c为光速；n为光纤折射率；η为线性扫频速率。

1.2 OFDR 光纤传感器应变测量原理

OFDR 分布式光纤利用纤芯中的高密度弱反射光纤光栅实现应变的测量，高密度弱反射光纤光栅传感器如图2 所示。

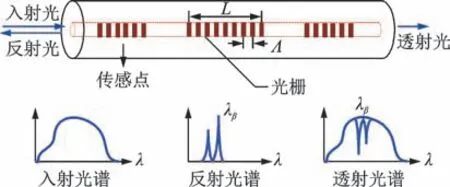
图2 高密度弱反射光栅传感器示意图Fig.2 Schematic diagram of high-density weak reflection grating sensors

当一束宽带光传输到传感器栅区时，在栅区折射率周期性作用下，只有特定波长的光信号被反射。该特定波长称之为中心波长λB，中心波长取决于光栅周期Λ与有效折射率neff，根据模式耦合理论，反射光谱中心波长表达式为

任何引起光栅周期Λ、有效折射率neff变化的因素都可以使传感器中心波长发生偏移，正是根据这一原理，光栅传感器具有传感能力。

当存在温度或者应力作用于某一光栅时，若其中心波长偏移量为Δλ，则对应的频移［9］为

由于光源是线性扫频光，频移Δf引入的时延τz为

其中：η为光源线性扫频速度。

由式（6）可知，求解光栅波长偏移量的关键是时延τz，而通过上述信号间的互相关分析便能获得时延。因此，经式（5）可计算得到布拉格光栅波长偏移量为

光栅中心波长偏移与应变、温度的关系［10］为

其中：ΔT为温度变化量；ε为光纤所受应变；Kε为光栅应变灵敏度系数；KT为光栅温度灵敏度系数。

假设待测OFDR 分布式光纤所处环境恒温，光纤仅受应力作用，由式（7）和式（8）可知，OFDR 分布式光纤所测应变为

2 复合材料层板冲击有限元仿真

2.1 复合材料层板冲击有限元仿真模型

采用有限元分析软件ABAQUS 建立复合材料层板结构冲击仿真模型，如图3 所示，仿真模块选择显示动力学模块。锤头为半径7.5 mm 的半球形锤头，锤体长为40 mm，密度为7.8 g/cm3，弹性模量为210 GPa，泊松比为0.3。复合材料层板尺寸为400 mm×400 mm×2 mm，每层铺层厚度为0.2 mm，共铺设5 层，铺层形式自下而上为［45°/0°/-45°/90°/45°］，铺层基本材料属性如表1 所示。采用四端固支方式，冲击锤距离复合材料层板上表面1 mm。

表1 铺层基本材料属性Tab.1 Basic material properties of ply

图3 复合材料层板冲击仿真模型Fig.3 Impact simulation model of composite material board

2.2 有限元仿真结果分析

为探究复合材料层板在不同位置冲击作用下的应变分布与变化规律，分别选择板面3 个代表性坐标位置作为冲击点。以复合材料层板上侧表面左下角为坐标原点O，建立相应直角坐标系，模拟冲击点坐标如图4 所示。

图4 模拟冲击点位置示意图（单位：mm）Fig.4 Schematic diagram of simulated impact pointlocation (unit:mm)

速度为5 m/s 时，冲击点a和b对应的复合材料层板表面应变响应云图如图5 所示。由图可知，应变幅值最大处位于冲击点所在位置，且距离冲击点越远应变幅值越小。进一步对板面典型路径下不同时刻的应变响应进行分析，冲击点a对应的不同应变提取路径如图6 所示，冲击点a引起的板面AB路径上不同时刻的应变响应曲线如图7 所示。

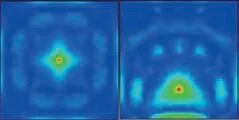
图5 冲击点a 和b 应变响应分布云图Fig.5 Strain response distribution of impact point a and b

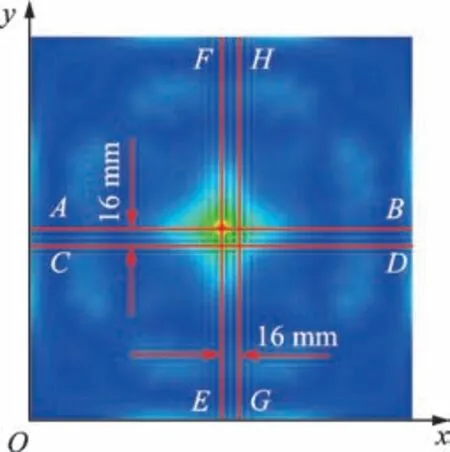
图6 冲击点a 对应的不同应变提取路径Fig.6 Extraction diagram of different strain paths at impact point a

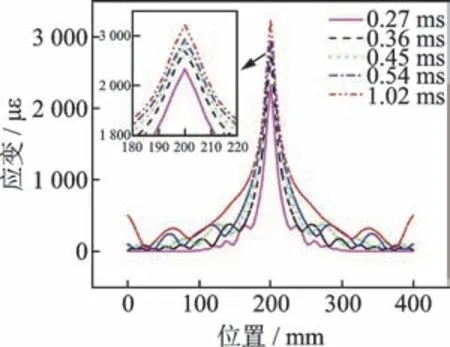
图7 冲击点a 对应的路径AB 应变响应曲线Fig.7 Strain response curve of path AB corresponding to impact point a

由图7 可以看出，峰值对应的x，y方向坐标与冲击点a所在位置完全对应。在同一时刻，应变幅值沿着冲击点a两侧呈指数形式衰减，即冲击载荷所在位置的应变大于该路径其他位置应变。因此，可以通过测量并对比该路径上各传感点的应变响应来确定冲击点所在位置坐标。考虑到实际冲击载荷加载位置的随机性，在x和y方向布置的应变感知路径通常与冲击点存在一定距离。

本研究选取冲击速度为2.5，5 和10 m/s 时，对于冲击点位置a给出提取路径CD上不同冲击速度对应的应变响应曲线，如图8 所示。由图可知：随着冲击速度的增大，相应路径的应变峰值逐渐增大.由于冲击点a与路径CD存在一定的距离，使得相应路径的应变响应曲线出现较宽的应变集中区域，应变幅值也相应减小，但应变响应峰值所在坐标仍与冲击点a所在位置基本对应。

图8 冲击点a 对应的路径CD 应变响应曲线Fig.8 Strain response curve of path CD corresponding to impact point a

3 冲击定位原理与算法仿真验证

3.1 应变幅值非线性加权定位算法原理

质心定位算法是一种无需测距的定位算法［11］，仅需传感节点的位置信息。然而，质心定位算法属于一种粗精度定位算法，其精度取决于待定位点附近传感器的数量及分布情况。假设传感器节点分别为S1，S2，…，Si，实际待定位点为So，则基于传感器节点的定位预测坐标为Se（xe，ye）

由式（10）可知，待定位点的坐标预测仅依靠传感节点的位置信息，并未考虑传感节点所测物理量特征与待定位点坐标之间的联系［12］。应变响应幅值随着冲击点与传感节点距离的增大而呈现指数形式衰减［13］，传感器所测应变越大，表明该传感器距离冲击点越近。本研究在传统质心加权定位方法基础上，提出基于应变幅值非线性加权的质心定位方法，用以提高冲击定位的精度。

其中：m为权函数w的加权次数；函数gi为第i个应变值占监测区域内应变测量总值的比例函数。

根据上述分析，可得到应变非线性加权质心法对应的坐标计算方法为

加权次数m的选择应以定位误差目标函数最小为准则。定义定位误差目标函数Eall(n)为n个冲击位置预测坐标绝对值误差的平均，即

其中：LEi为第i个冲击点预测坐标绝对误差值。

3.2 算法仿真验证

为验证基于应变幅值非线性加权质心定位算法的可行性，随机选取8 个不同位置的代表性冲击点，各点坐标如表2 所示。设置2 条经过板面中心且与x，y坐标轴分别平行的应变提取路径MN和PQ，模拟冲击点位置及路径提取如图9 所示。

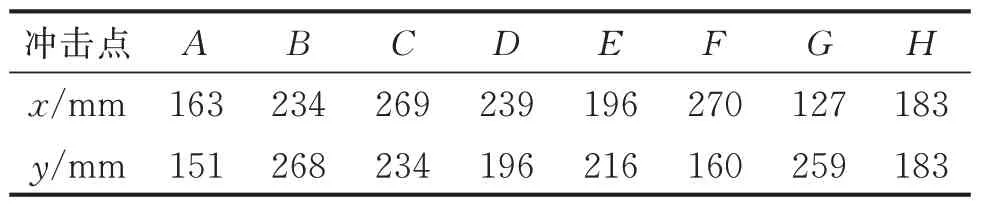
表2 冲击点坐标Tab.2 Impact point coordinates

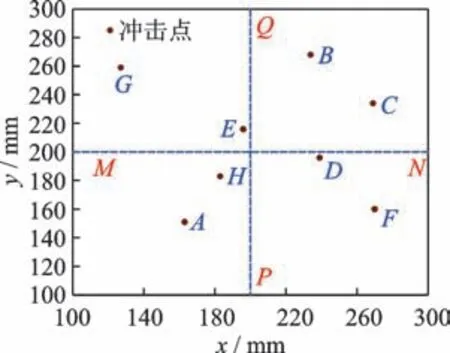
图9 模拟冲击点位置及路径提取示意图Fig.9 Schematic diagram of simulated impact point location and path extraction

不同加权值m对应的定位误差平均值曲线如图10 所示。当m=0.1 时，各个冲击点定位误差的平均值最小；当m在0.01～0.1 之间取值时，误差平均值变化平缓；当加权值m在0.1～10 之间取值时，误差平均值随着m增大而快速增加。因此，通过优化非线性加权系数可以减小定位误差。

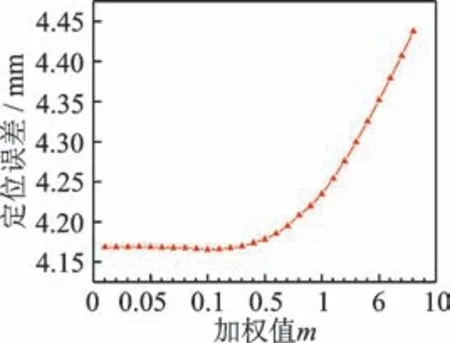
图10 不同加权值m 对应的定位误差平均值曲线Fig.10 Average localization error curve corresponding to different weight values m

4 OFDR 光纤传感器应变敏感特性

4.1 应变敏感特性试验系统

在复合材料层板表面沿x，y方向分别粘贴一段长度为190 mm×190 mm 的OFDR 分布式光纤传感器，每个方向各有30 个传感节点。OFDR 分布式光纤传感器布局与加载点位置如图11 所示，其中：1#～30#为x方向传感节点编号；31#～60#为y方向传感节点编号。在x，y方向各等间距布置8 个冲击加载点，相邻加载点间距为10 mm，其中y方向加载点距y方向光纤72 mm，y方向加载点a距x方向光纤10 mm。类似地，x方向加载点距x方向光纤51 mm，x方向加载点i距y方向光纤10 mm。

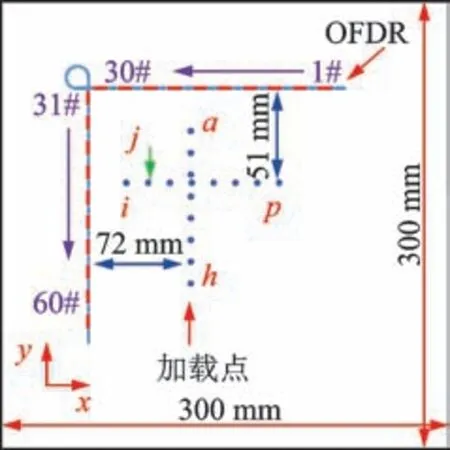
图11 OFDR 分布式光纤传感器布局与加载位置Fig.11 Schematic diagram of OFDR fiber optic sensor layout and loading position

4.2 OFDR 光纤传感器冲击响应特性

以图11 所示加载点进行冲击试验，采用不锈钢珠通过一定下落高度来模拟冲击过程。根据试验结果可得，OFDR 分布式光纤传感器内部第18#，19#和20#传感节点分别对应冲击加载点a～h，其应变响应变化峰值与冲击加载距离之间的关系见图12。由图可知，当冲击能量固定时，在0～7 cm 的范围内，随着冲击距离的增加，相关传感节点所测动态应变响应变化峰值逐渐减小，且趋于平缓。考虑到光纤信号受噪声及漂移影响，存在约2～3 με 波动，因此OFDR 光纤传感器能够感受冲击响应的有效范围约在0～7 cm 之间。

图12 应变响应变化峰值与冲击距离变化规律Fig.12 The change law of strain response peak value and impact distance

5 复合材料层板光纤冲击定位试验

5.1 复合材料层板冲击定位监测试验系统

复合材料层板冲击定位监测试验系统如图13所示，主要由复合材料层板、OFDR 分布式光纤传感器、光频域反射型光纤解调仪以及计算机组成。复合材料层板尺寸为600 mm×600 mm×2 mm，采用PCB 力锤施加冲击载荷。

图13 复合材料层板冲击定位监测系统Fig.13 Schematic diagram of impact localization results of composite panels

试验监测区域大小为280 mm×280 mm，复合材料层板表面粘贴的OFDR 分布式光纤传感器布局形式经优化后，如图14 所示。

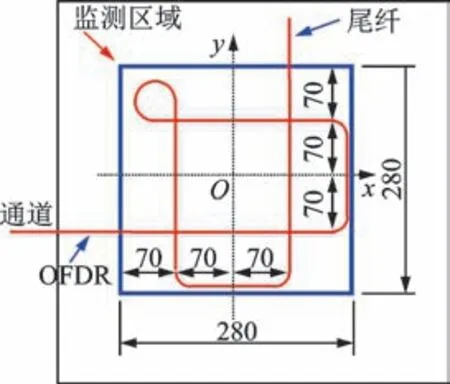
图14 复合材料层板OFDR分布式光纤优化布局（单位：mm）Fig.14 Optimized layout of OFDR distributed optical fiber on composite material board (unit:mm)

5.2 冲击定位结果分析

为验证应变幅值非线性加权冲击定位算法，基于分布式光纤优化布局，对复合材料层板随机施加16 次冲击。复合材料层板冲击定位结果如图15 所示，选取了不同加权值进行定位预测。各冲击点在不同加权值下相应冲击点定位误差如图16 所示。

图15 复合材料层板冲击定位结果示意图Fig.15 Schematic diagram of impact localization results of composite panels

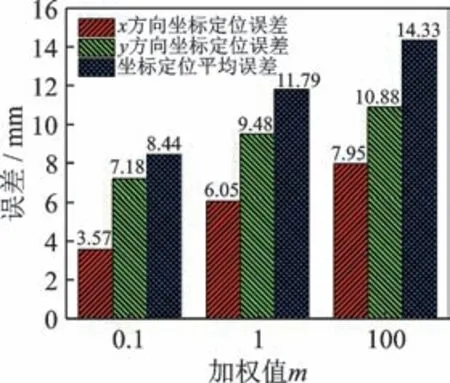
图16 不同加权值m 对应的冲击点定位误差Fig.16 Location error of impact point under different weights

由图16 可以看出：当加权值为0.1 时，16 个冲击点的平均定位误差为8.44 mm；加权值为1 和100时，平均定位误差分别为11.79 和14.33 mm。当加权值为0.1 时，冲击点预测的x坐标与y坐标平均误差均显著小于加权值为1 和100 的定位结果，因此选取合理的应变幅值非线性加权系数，可以提高冲击定位精度。