时变路径行星齿轮箱太阳轮故障响应周期特性∗
2023-11-06张旭龙章翔峰
张旭龙,姜 宏,章翔峰,李 军,申 勇,丁 韬
(新疆大学机械工程学院 乌鲁木齐,830047)
引言
由于行星齿轮箱具有体积小、传动比大及承载能力强等优点,被广泛应用于风力发电等大型机械设备中[1]。太阳轮作为其关键零部件极易发生故障[2],由于故障振动信号存在严重时变路径调制,常规分析方法难以实现运行状态监测,太阳轮故障类型的诊断更为困难。对时变路径特性进行深入研究,有助于找寻太阳轮不同故障间的差异性。
行星齿轮箱系统中,太阳轮故障啮合响应时变路径特性将增强太阳轮不同类型故障间的差异。传递路径长短不同,则故障响应衰减和受到路径调制不同,这种变化具有一定的周期性[3]。冯志鹏等[4]通过研究传递路径对振动信号的影响,指出当传感器安装在箱体特定位置,接收到的太阳轮故障振动信号传递路径存在时变现象,造成信号幅值大小周期性变化。孟玲霞等[5]通过研究行星齿轮箱振动信号模型,指出箱体上特定位置传感器随着故障啮合点的转动,存在振源传递路径长度变化,造成接收信号强弱变化。以箱体特定位置传感器为观测点,太阳轮故障啮合点转动时,传感器接收故障啮合响应的传递路径长度以一定周期变化;同时,太阳轮故障齿与特定行星轮啮合位置周期性变化。上述2 个周期性变化都以太阳轮轴为中心,存在最小公共周期。太阳轮故障啮合响应的周期性,本质是由信号传递路径时变性引起,特定位置传感器通过时变路径采集到的故障响应,在最小公共周期内具有相对唯一性。此周期包含的数据能够反映太阳轮不同类型故障之间的差异性,有利于对太阳轮不同类型故障诊断的深入研究。
文献[4]对时变路径的周期性变化结合模型进行了分析,推导出行星齿轮箱齿轮局部故障振动频谱特征,并应用于故障分析中。Lewicki 等[6]以行星架作为太阳轮故障啮合位置周期性变化的参考系,对最小啮合周期做了一般性推导,并应用于行星齿轮箱故障诊断中。赵磊等[7]应用特定行星齿轮箱,基于时变路径影响下的故障啮合周期分析,用加窗的方式将行星齿轮箱振动信号进行分离,诊断出齿轮齿根裂纹故障。张冕等[8]基于太阳轮和行星架的旋转角度,获得了最小啮合周期的一般表达式。
笔者为了确定能够表征太阳轮不同故障类型的数据长度,首先,经振动信号传递路径分析确定了传感器定点采集的方式,考虑行星轮之间是否存在差异性,分别推导出对应的周期表达式;其次,借助周期表达式,以特征为坐标建立3 维空间分离太阳轮不同故障类型;最后,通过分离效果确定数据长度。
1 时变路径周期啮合特性
采集故障响应的传感器一般布置在行星齿轮箱箱体上,太阳轮故障齿与行星轮齿啮合产生的响应将通过3 条不同路径到达传感器。行星齿轮箱模型及太阳轮故障啮合传递路径如图1 所示。第1 条路径由故障啮合位置,经过行星轮传递给箱体,由箱体上的传感器进行采集;第2 条路径由故障啮合位置,经行星轮、行星轮轴承、行星架、行星架轴及行星架轴承传递至箱体,由箱体上的传感器进行采集;第3条路径由故障啮合位置,经太阳轮、太阳轮轴及太阳轮轴承传递至箱体,由箱体上的传感器进行采集[9]。第2、第3 条传递路径的距离不会随着故障啮合位置变化,对振动信号只产生比例缩放作用,不会产生调制作用[4]。路径1 的传递距离随时变化,对故障响应产生调制,这种时变特性是太阳轮故障响应最显著的特征,因此将传递路径1 作为本研究的重点。
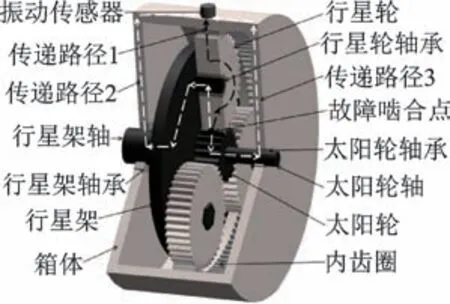
图1 行星齿轮箱模型及太阳轮故障啮合传递路径Fig.1 Planetary gearbox model and description of transmission path of sun wheel fault meshing
随着太阳轮旋转,太阳轮故障轮齿不断与不同行星轮齿啮合,啮合位置不停变化,传递路径1 响应路线也不断变化[10]。传递路径1 长度变化如图2 所示,时变路径越短则信号传递能量越强,时变路径越长则信号衰减越严重[11]。

图2 传递路径1 长度变化Fig.2 Transfer path 1 length change
将特定位置传感器作为太阳轮故障啮合位置周期性变化的观测点(如图2 中将箱体顶部传感器作为固定观测点),由图2 可以看出,随着轮系的周期性转动,传递路径1 不断地发生周期性变化,呈现出太阳轮故障传递路径的时变特性[11]。因为太阳轮、行星架都以太阳轮轴心为中心转动,所以太阳轮故障齿和特定行星轮齿啮合响应经传递路径1 被传感器采集的过程存在最小周期。例如,图2(a)传递路径最短,图2(b)传递路径由最短逐渐变长,图2(c)传递路径最长,图2(d)传递路径由最长逐渐变短,再恢复至图2(a)位置;随着故障啮合位置周期性变化,传递路径1 长度也周期性变化。当传感器位置固定时,故障啮合位置变化周期内传感器采集到的振动信号也具有周期性,周期内振动数据能表征太阳轮不同类型故障啮合响应特性。
2 啮合周期特性推导
行星齿轮传动系统结构如图3 所示,其中:s 为太阳轮;r 为行星轮;p 为内齿圈;H 为行星架。
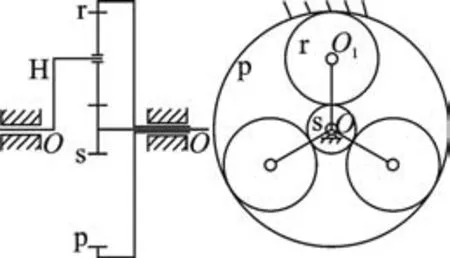
图3 行星齿轮传动系统结构Fig.3 Structure of planetary gear transmission system
太阳轮与行星架的转速比为
其中:isH为太阳轮与行星架的转速比;ωs为太阳轮转速;ωH为行星架转速;Zs为太阳轮齿数;Zr为内齿圈齿数。
由式(1)可知,任意时间段td内太阳轮和行星架转过圈数之比为
2.1 行星轮存在差异的同齿啮合周期
行星轮系中,安装、制造加工造成各行星轮之间存在轴心对中及物理形状的差异,导致各行星轮与太阳轮故障轮齿啮合状态的差异。太阳轮故障齿与每一个行星轮的啮合响应将这种差异经传递路径1被传感器采集。太阳轮发生单齿故障,任意时刻故障啮合点与同一位置再次出现故障轮齿与同一行星轮齿啮合,其时间间隔ts为太阳轮故障啮合最小周期,定义为同齿啮合周期(从开始转动到1 个周期结束时,太阳轮故障轮齿仍然与同一个行星轮上的齿在同一位置啮合),同齿啮合周期原理如图4 所示。

图4 同齿啮合周期原理Fig.4 Principle of meshing period of the same gear teeth
对各行星齿轮之间存在差异时的太阳轮啮合特性进行分析,此时td=ts,并且太阳轮转过的角度θs与行星架转过的角度θH有以下关系
太阳轮旋转圈数为正整数,结合式(3)可判断,行星架转过圈数也为正整数。太阳轮故障啮合最小周期需要满足式(2)和式(3),同时要取得最小值,即
其中:Gmin(Zs+Zr,Zs) 为Zs+Zr与Zs的最小公倍数。
因此,太阳轮故障啮合最小周期为
为方便表述,后文论述时将行星轮之间存在差异时的同齿啮合周期统一用ts表示。
2.2 各行星轮完全相同的准同齿啮合周期
理想状态时各行星轮完全相同,与太阳轮啮合状态一致。太阳轮故障啮合最小周期不考虑行星轮之间的差异,只与太阳轮旋转方向下一个行星轮齿啮合时位置相关,定义为准同齿啮合周期(从开始转动到1 个周期结束,太阳轮故障齿与太阳轮旋转方向下一个行星轮齿在同一位置啮合),准同齿啮合周期原理如图5 所示。
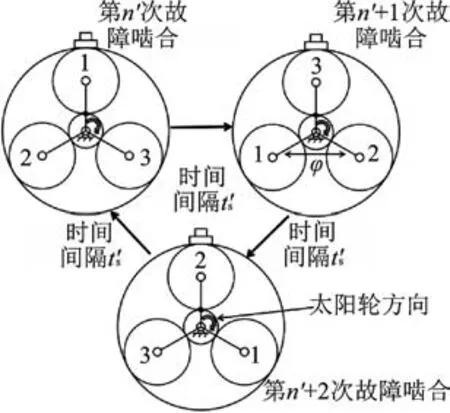
图5 准同齿啮合周期原理Fig.5 The principle of meshing period of quasi-identical teeth
其中:a为太阳轮多转过角度的个数;分别为时间段内太阳轮和行星架转过的圈数。
太阳轮旋转圈数为正整数,结合式(7)可知,行星架旋转圈数可为正整数或者正分数。
其中:Gmin(Zs+Zr,Zs) 为Zs+Zr与Zs的最小公倍数。
由式(4)、式(10)可得
行星轮完全相同时太阳轮故障啮合最小周期为
为方便表述,后文论述将各行星轮完全相同时的准同齿啮合周期统一用表示。
2.4 施工安全与企业信誉的关系信誉是一种隐形效益,是企业多年经营后所获得的社会对企业的评价。施工安全是企业信誉的一个非常重要的方面。一个高信誉的企业必定是个安全工作做得完善的企业。因为信誉高是企业综合素质的反映,当然包括在安全方面的出色管理。建筑企业欲在当今市场中求发展,做好施工安全管理是极其重要的一环。创造信誉得靠人为,人的安全无保证,怎能去创信誉。企业要获得信誉,先要保证开创信誉人的安全。
3 实验数据分析
3.1 分析方法
根据式(12),综合考虑ts及之间的关系,构造经传递路径1 传感器采集到的太阳轮单齿故障振动信号为
太阳轮单齿故障振动信号分析如下。
1)本研究重点关注太阳轮单齿故障振动信号,对于特定行星系统,相同转速下产生的系统噪音在啮合周期内基本相同[8]。行星轮和内齿圈都为健康齿,啮合周期内基本相同。分析太阳轮不同类型故障啮合特性时可以忽略系统噪音和的影响,重点关注。
2)M<N时,因为行星齿轮制造和安装所产生的误差不可避免,准同齿啮合周期或者其倍数内故障数据没有完全包含啮合响应特性,不足以表征不同状态太阳轮之间的差异性。
3)M=N时,同齿啮合周期内数据包含完整啮合响应特性。太阳轮故障类型不同,啮合响应不同,能够表征不同状态太阳轮之间的差异性。
4)M>N时,同齿啮合周期与准同齿啮合周期同时存在,数据包含超过一个完整同齿啮合周期的响应特性,对不同状态太阳轮之间差异性表征不断增强。
3.2 实验验证
通过太阳轮不同故障类型实验数据,结合ts及t's,探究表征太阳轮故障差异性的数据长度。采用图6 所示的行星齿轮传动系统动态测试实验台采集振动信号,实验平台由驱动电机、控制器、平行轴齿轮箱、行星齿轮箱及磁粉制动器等组成。行星轮系参数如下:太阳轮齿数为20;行星轮齿数为40;内齿圈齿数为100。

图6 行星齿轮传动系统动态测试实验台Fig.6 Test table for dynamic test of planetary gear transmission system
由式(5)、式(12)可知,ts和与齿轮转速直接相关,通过验证不同转速对应啮合周期的数据,才能充分验证ts和表达式的准确性。在转速为2 100,2 400 和3 000 r/min 时采集太阳轮的故障信号,其故障类型如图7 所示。

图7 太阳轮故障类型Fig.7 Type of solar wheel fault
啮合周期及其倍数内的数据可代表太阳轮不同类型的故障信息。选择有代表性的特征表征啮合周期内太阳轮不同类型故障振动信号的差异性:方差表示数据周期性偏离程度;均方根表示振动信号能量变化;峭度值表示振动信号冲击分布特性。对采集的振动信号利用和ts及其倍数进行截取。借助上述特征建立3 维空间进行故障诊断,并确定表征不同故障类型的数据长度,故障诊断流程见图8。
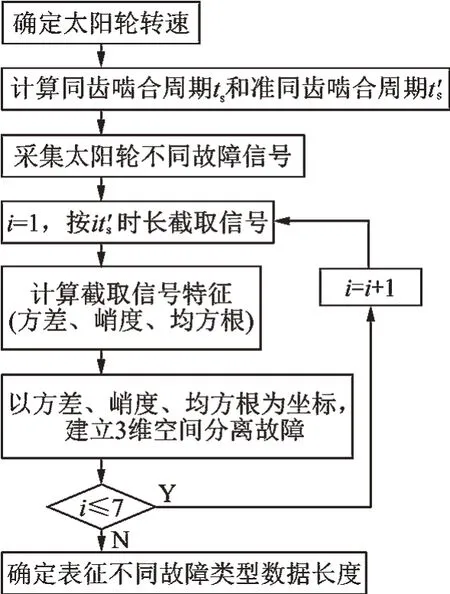
图8 故障诊断流程图Fig.8 Flow chart of fault diagnosis
通过式(5)和式(12),计算不同转速下太阳轮故障振动信号啮合周期,如表1 所示。
由表1 可知,当转速为2 100 r/min 时,同齿啮合周期ts=0.171 s,准同齿啮合周期。分别采集健康太阳轮、太阳轮齿根裂纹及太阳轮齿面磨损信号各20 组,共60 组,每组时长为5 s,按照图8的流程对信号进行处理。通过计算截取信号的特征值,并以其为坐标建立3 维空间,将各组信号转化成空间中的点,对不同类型故障对应点用不同符号表示,通过相同符号点在空间中聚集程度体现对不同类型太阳轮故障的区分效果,转速为2 100 r/min 时的诊断结果如图9 所示(峭度值无量纲)。
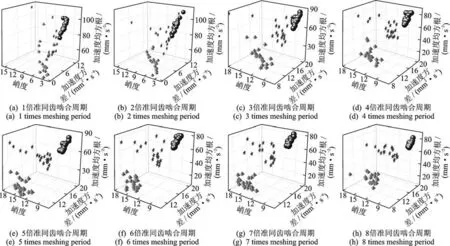
图9 转速为2 100 r/min 的诊断结果Fig.9 Diagnostic results at 2 100 r/min
图9(a)~(c)中3 维空间各点散乱分布,代表太阳轮相同的故障点未在空间内形成聚集区域,说明内数据之间的差异性不明显。随着数据长度接近4t's,相同符号点有聚集的趋势。
图9(e)~(g)中,代表太阳轮相同的故障点集中在一定区域,相同符号聚集空间分界明显,说明健康太阳轮和太阳轮齿面磨损的点在空间中的位置已经基本稳定,代表太阳轮齿根裂纹的点逐渐集中。
采用相同的方法对太阳轮转速为2 400 和3 000 r/min 时的信号进行处理,诊断结果分别如图10,11 所示。其中,与相对应的3 维空间内各点散乱分布,代表太阳轮相同的故障点未在空间内形成聚集区域。这说明太阳轮转速变化后,重新计算所得内数据之间差异性仍不明显,不足以区分太阳轮的不同状态,与图9 中的结果相同。
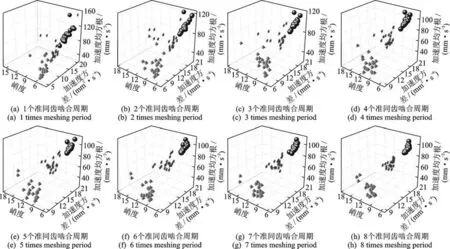
图10 转速为2 400 r/min 的诊断结果Fig.10 Diagnostic results at 2 400 r/min

图11 转速为3 000 r/min 的诊断结果Fig.11 Diagnostic results at 3 000 r/min
4 结论
1)通过对太阳轮故障啮合响应传递时变路径特性的分析,说明了太阳轮故障啮合最小周期的存在。根据太阳轮与行星架的转速比,推导出“同齿啮合周期”和“准同齿啮合周期”的表达式,并证明了两者之间的关系。
2)结合同齿啮合周期和准同齿啮合周期之间的关系,构造出太阳轮单齿故障振动信号的表达式。分析可知,同齿啮合周期及其倍数内的信号长度数据更能反应行星系统中行星轮之间存在差异性的真实工况。
