一角点支撑对面两边固支正交各向异性矩形薄板弯曲问题的辛叠加解

寇天娇,额布日力吐

(内蒙古大学数学科学学院,内蒙古 呼和浩特010021)

1.引言

各向异性矩形板是土木工程、航空航天以及机械制造等各种现代工程中普遍应用的一种结构元件.由于各向异性矩形板的基本方程为高阶多变量的偏微分方程,因此一般很难得到其精确的解析解[1].近年来,国内外学者不断探索怎样寻求各向异性矩形板方程的解析解,并得到了一些解析方法,如叠加方法[2]、复变函数法[3]、有限积分变换法[4]和傅立叶级数法[5]等.但是上述方法都属于半逆解法或者基于半逆解法的方法,这类方法需要事先人为设定挠度等试验函数,而选取的函数无规律可循,不具有普适性.

直到二十世纪九十年代初,钟万勰教授巧妙的在弹性力学中引入了辛几何方法[6−7],为弹性力学的发展画上了点睛之笔.2010年李锐等学者[8]又在辛弹性力学方法的基础上提出了辛叠加方法,这进一步拓宽了辛弹性力学方法求力学问题解析解的范围.

辛叠加方法到目前已解决了一系列各向同性板弯曲[9]与振动[10]的实际问题,丰富了各向同性板问题的解析求解,然而各向异性板由于其自身的复杂性,致使辛叠加方法还未能广泛应用到各向异性板的实际问题当中.文[9]研究了均匀荷载下一角点支撑对面两边固支的各向同性板弯曲问题,而本文应用辛叠加方法进一步研究了均匀荷载下一角点支撑对面两边固支的正交各向异性矩形薄板弯曲问题.首先,根据对边简支边界条件下原方程所对应的Hamilton算子本征函数系的完备性,应用本征函数系的辛-Fourier展开得到对边简支问题所对应的Hamilton正则方程的通解,再利用叠加方法求出一角点支撑对面两边固支的正交各向异性矩形薄板弯曲问题的解析解.最后通过本文解析解计算的数值结果与已有文献的数值结果进行比较,验证了本文所得辛叠加解的正确性.

2.Hamilton正则方程

考虑正交各向异性矩形薄板的基本方程

3.本征值和本征函数系

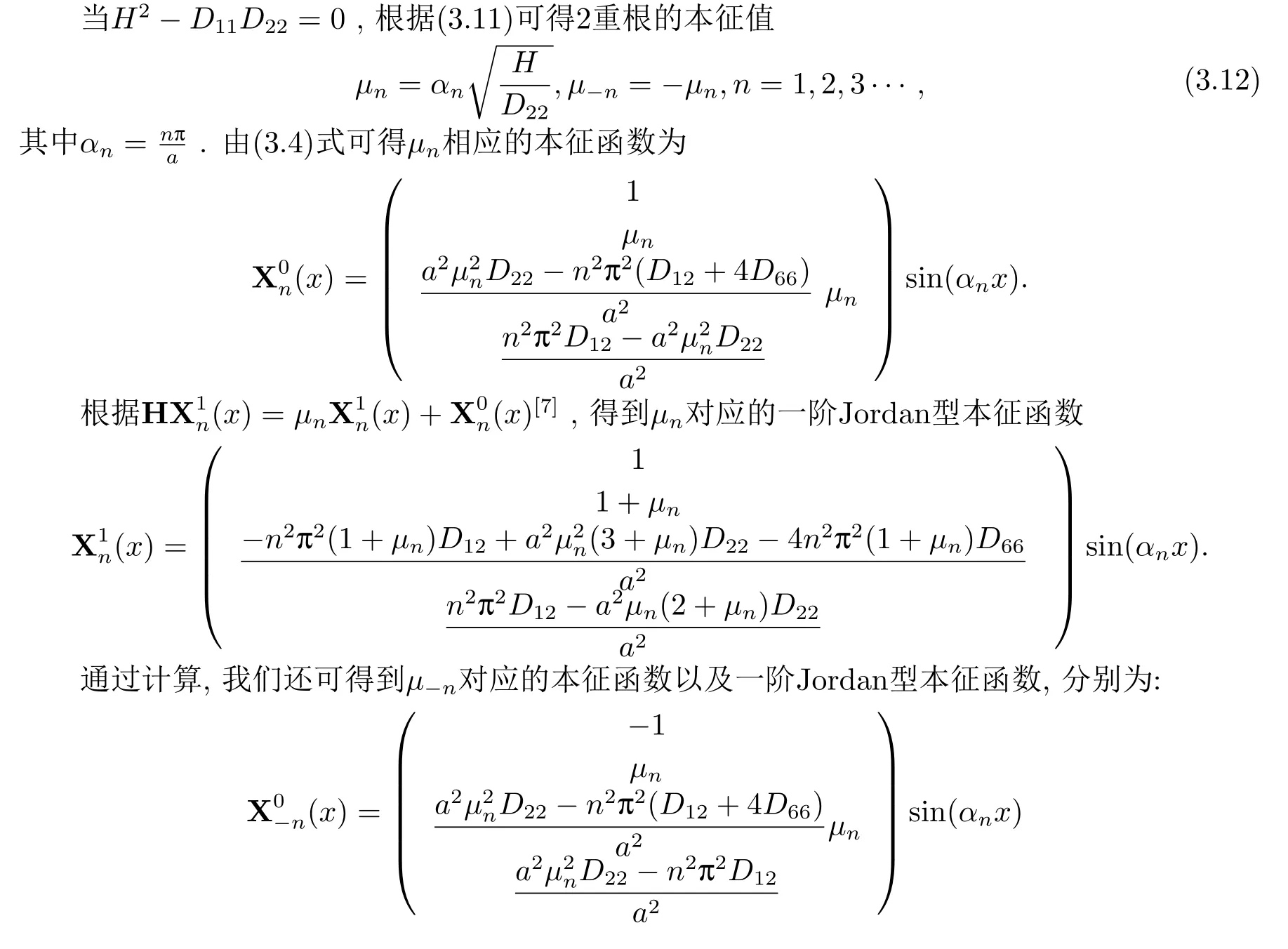
Ⅰ本征值为重根的情形

Ⅲ辛正交性与完备性

4.辛叠加解

为了研究均匀荷载作用下一角点支撑对面两边固支的正交各向异性矩形薄板弯曲问题,我们考虑如下三个子问题[9]:

(a) 四边简支正交各向异性矩形薄板在均匀荷载下的弯曲问题,在x=0和x=a边简支,在y=0和y=b边满足条件

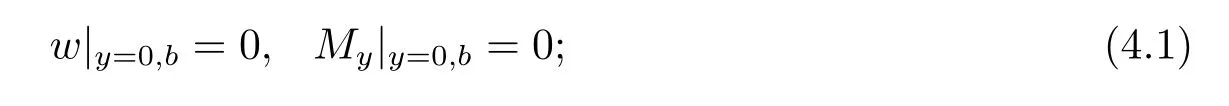
(b) 在x=0和x=a边简支,在y=0和y=b边满足条件

(c) 在y=0和y=b边简支,在x=0和x=a边满足条件

将上述三个子问题的解进行叠加后可得到均匀荷载作用下的一角点支撑对面两边固支的正交各向异性矩形薄板弯曲问题的辛叠加解.

Ⅰ本征值为重根情形下的辛叠加解

当H2−D11D22=0时,我们先来求解子问题(a),此时需要求解无穷维Hamilton正则方程(2.6),根据引理3,可设非齐次项

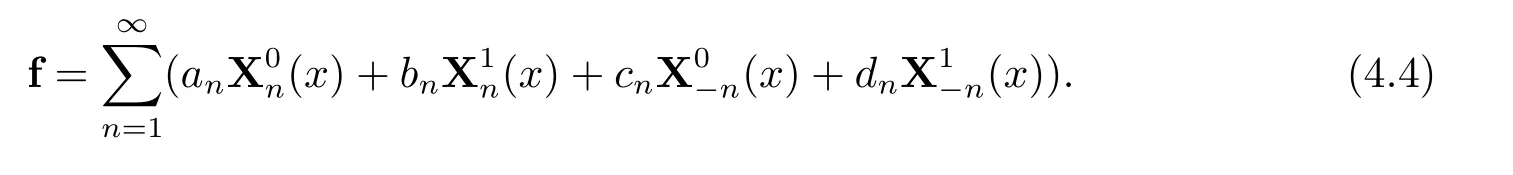
根据引理1,可得:

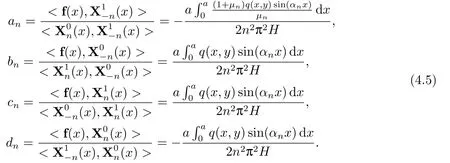
根据引理3,我们假设在边界条件(3.9)下Hamilton正则方程(2.6)的解为

在边y=0处,三个子问题的等效剪力之和应为零,即满足Vy|y=0=0,计算得到

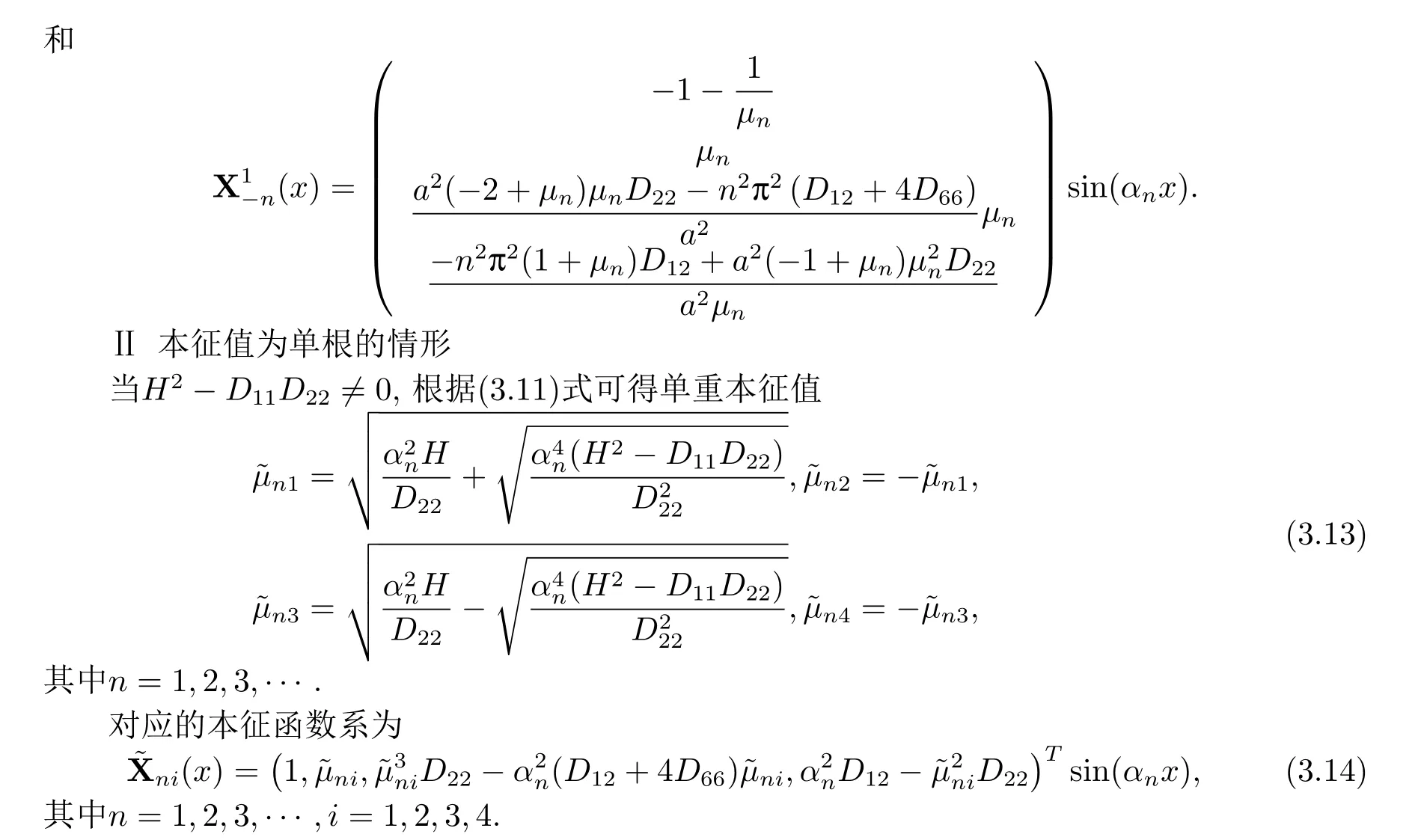
Ⅱ本征值为单根情形下的辛叠加解

类似于本征值为重根的情形,先求解子问题(a),即四边简支正交各向异性矩形薄板在均匀荷载下的弯曲问题.此时需设非齐次项

子问题(c)的通解为

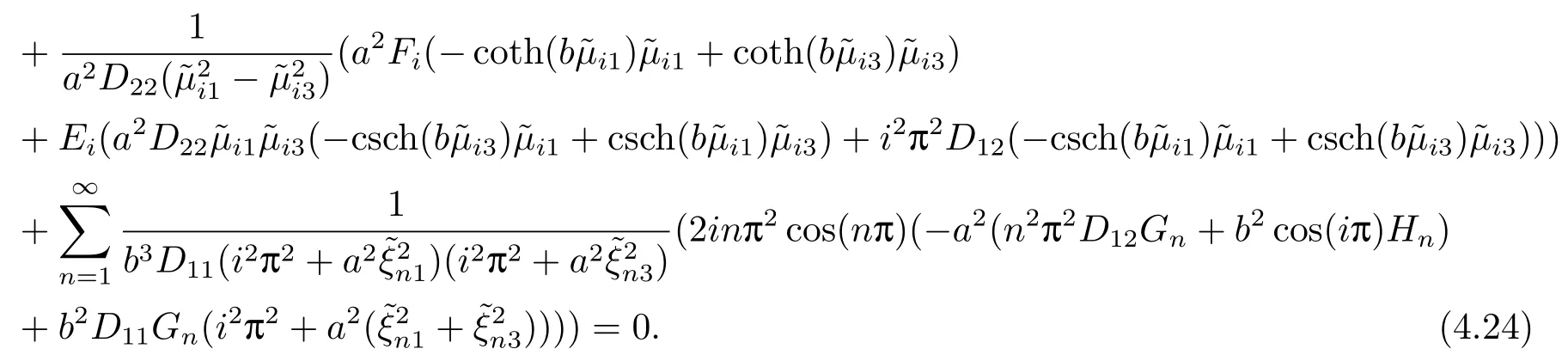
在边x=0处,三个子问题的等效剪力之和应为零,即满足Vx|x=0=0,计算得到

在支撑点(0,0)处,三个子问题的挠度之和应为零,计算得到

因为等式(4.27)恒成立,所以该式结果可忽略不计.通过求解方程组(4.23)-(4.26),解得系数En、Fn、Gn和Hn(n=1,2,3,...),将这些系数分别代入解(4.20),(4.21)和(4.22),我们得到本征值为单根情形下一角点支撑对面两边固支的正交各向异性矩形薄板弯曲问题的辛叠加解如下

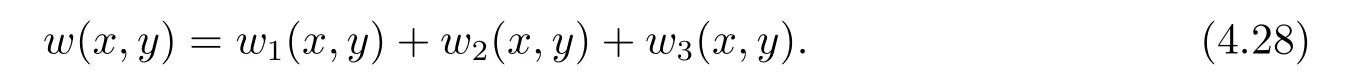
5.算例

这里我们分别计算了一角点支撑对面两边固支各向同性矩形薄板和正交各向异性矩形薄板一些点处的挠度和弯矩.为了丰富论文的计算数值结果,我们计算了b/a取不同值的一些结果，并将辛叠加解展开到前30项.

例1计算在均匀荷载下一角点支撑对面两边固支各向同性矩形薄板的挠度和弯矩,此时在正交各向异性矩形薄板方程(2.1)中的对应参数取为

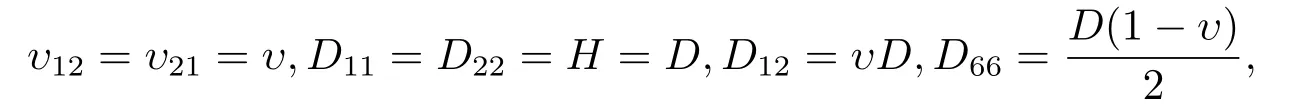
其中泊松比υ=0.3.计算数值结果(精度取到10−8)与文[9]的数值结果进行了比较,具体结果列于表1.

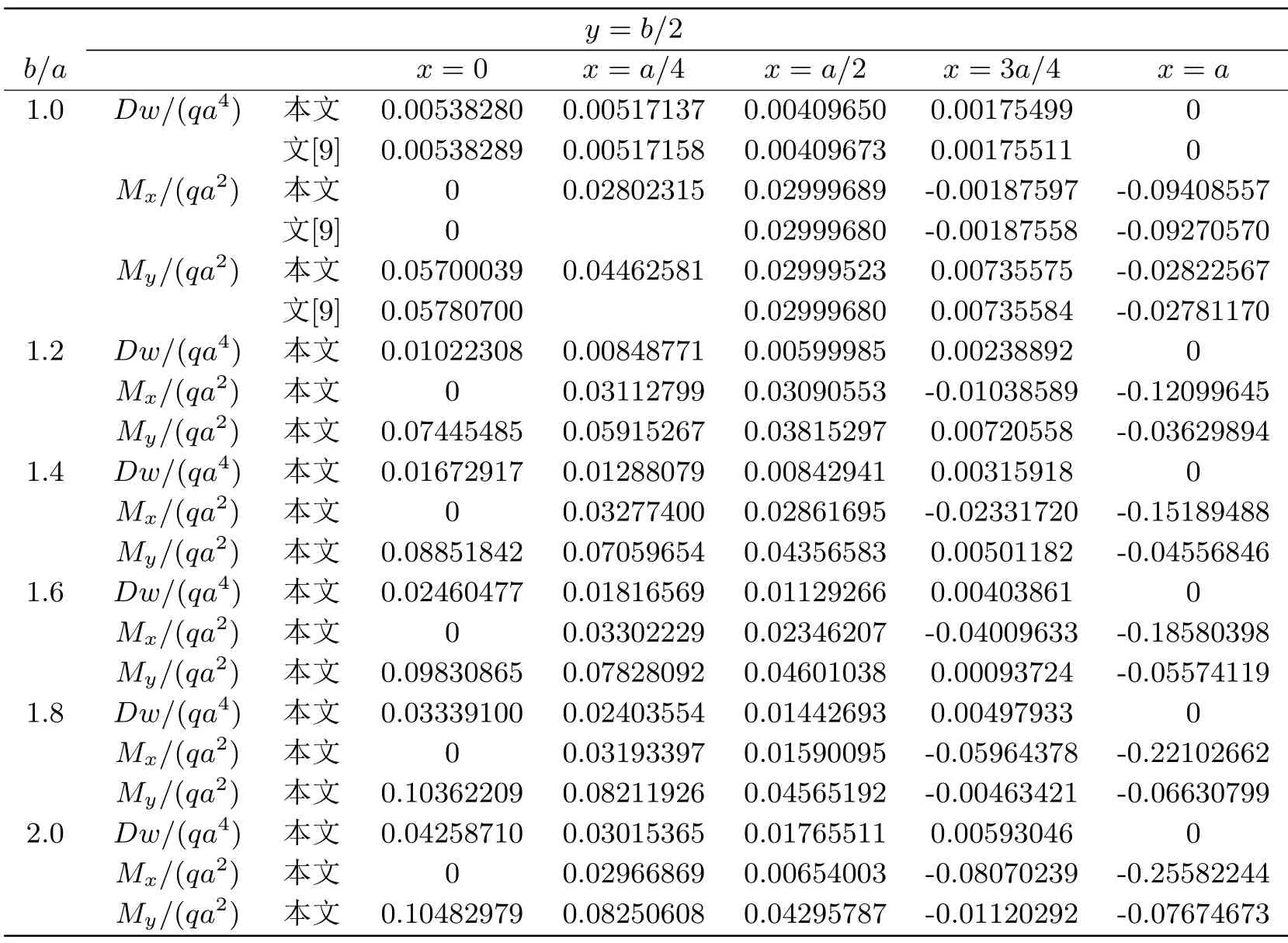
表1 均匀荷载下一角点支撑对面两边固支的同性矩形薄板的挠度和弯矩

例2计算了一角点支撑对面两边固支的正交各向异性矩形薄板的挠度和弯矩,取材料属性为

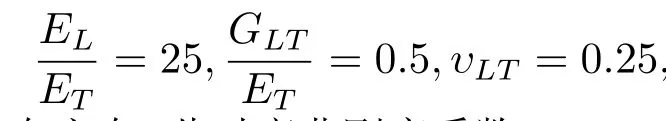
其中L和T分别表示纤维和横向方向.此时弯曲刚度系数D11、D12、D22和D66分别取

D12=0.01D11,D22=0.04D11,D66=0.01995D11,

一些点处挠度和弯矩的计算结果(精度取到10−8)列于表2.

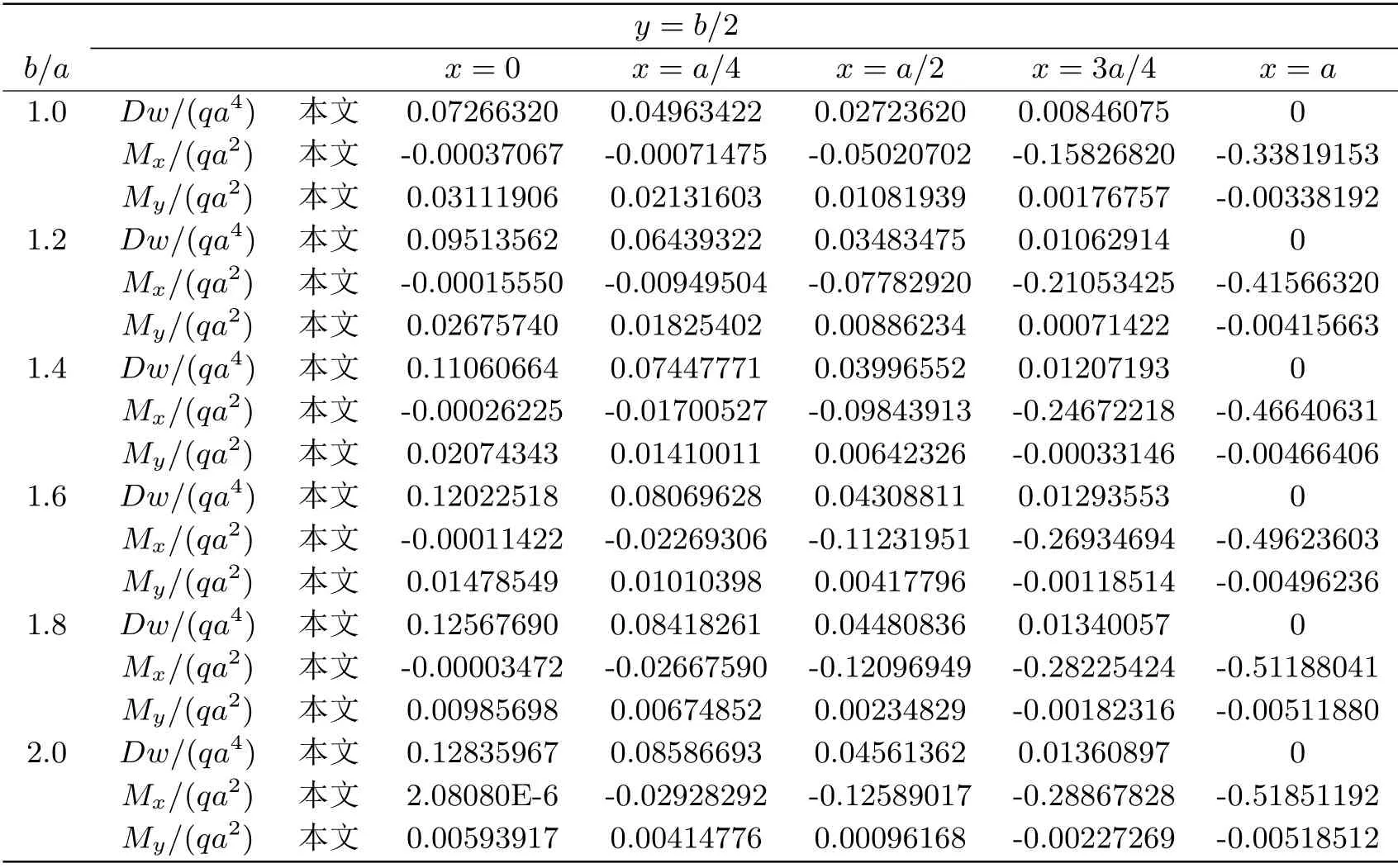
表2 均匀荷载下一角点支撑对面两边固支的正交各向异性矩形薄板的挠度和弯矩

6.结论

本文用辛叠加方法推导出了一角点支撑对面两边固支的正交各向异性矩形薄板弯曲问题的解析解.首先应用辛弹性力学方法得到了对边简支正交各向异性矩形薄板弯曲问题挠度形式的解,再利用叠加方法给出原问题的辛叠加解.虽然本文只计算了均匀荷载下一角点支撑对面两边固支的正交各向异性矩形薄板的挠度和弯矩值,但是应用本文给出的方法也可以研究任意荷载以及其他边界条件下的正交各向异性矩形薄板的弯曲和振动问题.