基于改进UKF 的非线性结构荷载和参数同步识别∗

王 振，辛 宇，2，王佐才，2，袁子青

（1.合肥工业大学土木与水利工程学院 合肥，230009）（2.安徽省基础设施安全检测与监测工程实验室 合肥，230009）

引言

工程结构在服役期间会遭遇各类不同的荷载激励，当结构处于较低水平荷载激励时，结构的行为符合线弹性假定［1］。然而，当其遭遇地震、强风等强荷载激励时，结构在一定程度上表现出较强的非线性动力学行为，其振动响应也表现出非平稳特性。利用基于振动响应的健康监测技术识别非线性结构的特征参数，不仅为非线性结构的损伤诊断提供重要支撑，同时对结构的安全评估具有重要意义［2-3］。然而在实际应用中，对于随机性较强的地震荷载，往往难以利用传感器设备精确获得结构外荷载的全部特征。因此，如何在输入荷载未知的情况下，开展非线性结构参数识别已成为结构健康监测领域亟待解决的一个难题。

近年来，国内外学者在未知荷载作用下结构参数识别研究领域已取得一定的成果。李杰等［4］将结构基底作用力作为识别过程的修正因子，提出全量补偿法和统计平均算法，并利用结构的动力响应数据识别出系统的物理参数，并反演地震动输入。Lu等［5］利用基于动态响应灵敏度的模型修正方法实现了对外荷载及系统参数的同步识别。Chen 等［6］提出了一种具有修正功能的迭代识别方法，将外部激励的空间信息转化为数学条件，通过运动方程对未知力矢量进行预测和修正，再基于修正后的输入力矢量对结构参数进行估计，并利用数值模拟验证了该方法的可行性。但当外荷载激励较强时，结构往往表现出非线性行为，此时上述线性系统识别方法将不再适用。

随着扩展卡尔曼滤波（extended Kalman filter，简称EKF）［7］和UKF 方法［8］的提出，基于时域信号的非线性结构参数识别技术得到了快速发展。相较于EKF，UKF 以无迹变换来近似计算非线性系统状态的后验均值和协方差，有效避免了雅克比矩阵的计算问题，显著提高了计算效率，并且在强非线性模型参数识别方面表现出优越性［9］。因此，在非线性系统识别中，UKF 方法得到了广泛应用［10-11］。文献 ［12-14］提出了一种基于UKF 的两阶段识别方法，首先利用最小二乘算法估计系统的外部荷载和子结构参数，再进一步结合传统UKF 方法对系统的非线性参数进行识别。尽管该方法能够实现未知激励下的非线性系统识别，但需要将系统的全部动力响应作为观测量。Ding 等［15］通过正交多项式对未知激励进行分解，并将正交多项式的系数作为未知参数进行识别，但该方法需要识别的未知参数数量过多，导致其计算效率较低。为了实现非线性参数和未知激励的同步识别，文献［16-17］提出了一种基于改进UKF 的非线性系统识别方法，利用递归非线性最小二乘方法对未知激励进行同步更新，能够有效地实现非线性系统参数和未知激励的同步识别，但当测量噪声水平较高时，该方法往往难以收敛到真实值。

笔者在传统UKF 方法的基础上，提出了一种改进UKF 的荷载和参数识别方法，能够有效实现结构状态参数与未知输入的同步识别。此外，为了降低测量噪声的影响，改善滤波器的跟踪性能，本研究进一步在提出的UKF 框架中嵌入线形卡尔曼滤波器，对测量噪声协方差矩阵进行同步优化。通过数值模拟验证了方法的可行性和精确性。

1 UKF 算法流程

假定离散非线性系统为

其中：k为离散时间；f(·)为非线性状态方程；h(·)为非线性测量函数；Xk为n维系统状态向量；zk为m维测量向量；uk-1为输入向量；vk～N(0，Qk)为过程噪声，服从高斯分布；wk～N(0，Rk)为观测噪声，服从高斯分布。

基于式（1）的UKF 状态估计过程如下。

1）初始化系统状态统计特性

2）选择采样策略，并计算sigma 点ξi，k-1(i=0，1，…，2n)，即

3）时间更新

4）测量更新

上述计算过程中的参数取值为

其中：λ=α2(n+κ)-n，α（0 ≤α≤1）为比例缩放因子，对于强非线性系统，α通常取一个较小的值；κ为比例参数，一般取κ=3-n或0；β为非权重系数，如果是高斯分布，β=2 为最优值；n为状态变量维数。

2 基于改进UKF 的非线性结构荷载及参数同步识别

2.1 荷载及参数同步识别方法

对于具有多自由度的非线性系统，其运动方程可表示为

其中：M，C分别为结构的质量矩阵和阻尼矩阵；分别为结构的位移、速度、加速度响应向量；θ为未知结构参数向量；R(x，θ)为系统恢复力；u为外荷载；L为荷载分布向量。

在输入荷载未知情况下，使用UKF 方法对结构状态和参数进行同步识别时，在k时间步，状态量更新完成后，采用预测状态量和测量值结合运动方程，对未知输入进行估计，即

其中：o 和p 分别为测量值和预测值；G(·)为非线性函数，G(·)中包含预估参数，需要在每一步进行更新。

在时间更新步中，利用k-1 步状态量Xk-1和输入uk-1，对k步状态进行预测，将状态预测值和测量值代入式（16）中，即可得到uk的估计值。将uk估计值代入到式（7）、式（8）中，即可求得测量预测值。此时得到的荷载估计值uk是不准确的，因为在uk的估计过程中，所使用的系统状态量和参数均为预测值，在后续计算中，估计误差将会被纳入到测量噪声中。

使用更新后的系统状态和参数对未知输入进行修正，即

用更新后的uk替换掉初始估计值，并在下一步预测中使用，重复上述过程，直至所有迭代全部完成。

具体识别流程如下。

1）初始化系统状态统计特性

2）计算sigma 点ξi，k-1(i=0，1，…，2n)

3）时间更新和未知输入估计

4）测量更新和未知输入更新

对于传统的基于UKF 的系统参数识别方法，测量噪声和过程噪声参数的协方差矩阵通常基于工程师经验进行设定，当这些假定的协方差矩阵与真实值差别较大时，可能会导致识别结果不准确甚至发散。为降低测量噪声对非线性系统识别的影响，本研究在进行荷载和参数的同步识别中，通过在UKF方法中嵌入KF 过程以实时优化测量噪声矩阵［18］，有效实现了非线性系统参数与未知输入的同步识别。KF 具体流程如下。

1）计算残差序列和残差序列协方差，即

2）KF 预测步。第k步测量噪声e的先验估计值和协方差为

其中：T为内嵌卡尔曼滤波过程的过程噪声协方差矩阵。

观测误差协方差矩阵的对角线为

3）KF 更新步。KF 的预测协方差和互协方差矩阵为

其中：U为内嵌卡尔曼滤波过程的观测噪声协方差矩阵。

KF 的卡尔曼滤波增益为

e的后验估计均值为

e的后验估计协方差矩阵为

观测噪声预测值为

T和U也是零均值高斯白噪声。将每次更新后的Rk代入到主滤波程序中，即可实现对噪声的自适应调整。

2.2 识别结果评价指标

为了验证未知激励识别的有效性，本研究通过定义相关系数来量化未知荷载的识别精度。相关系数的表达式为

其中：l为样本个数；yi为理论值；xi为识别值；为相应平均值。

相关系数r越接近于1，说明识别结果越接近于真实值。此外，基于先前研究结果［19］，当相关系数大于0.7 时，表明变量之间具有较好的相似性。

3 数值仿真分析

3.1 单自由度Bouc-Wen 模型算例

地震荷载作用下的单自由度Bouc-Wen 模型如图1 所示，其运动方程为

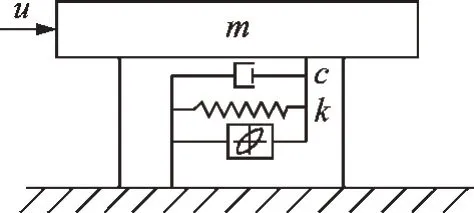
图1 单自由度Bouc-Wen 模型Fig.1 The single degree of freedom Bouc-Wen model

其中：u为地震激励；m，c分别为结构的质量和阻尼；x分别为结构的位移、速度和加速度；R(x，z，t)为系统恢复力；z为结构滞回位移。

Bouc-Wen 模型可以表示为

其中：k为结构刚度；α，β，γ，n为非线性参数。

本算例所用参数的数值如下：m=1 000 kg；c=0.3 (kN·s)/m；k=9 kN/m；α=0.1；β=2；γ=1；n=2。地震激励选用1940 年的El Centro 地震波，持续时间为30 s，采样频率为50 Hz。

本研究利用4 阶龙格库塔方法对式（43）状态方程进行求解，获取结构理论位移、速度和加速度响应。将结构的加速度和位移响应作为观测数据，并加入5%的高斯白噪声模拟测量噪声的影响。假设该系统的激励未知，选取k，α，β及γ作为模型的未知参数，将未知参数写入状态变量中，得到系统的广义状态向量，其状态空间方程式为

为了对未知系统的输入和参数进行同步识别，系统参数的初始值设置如下：X0=[x0，，z0，k0，α0，β0，γ0]T=[0，0，0，5.4，0.06，1.2，0.8]T；Q0=10-8I7×7；I为单位矩阵 ；R0=diag(1，10-3)。利用笔者提出的改进UKF 方法对该滞回系统进行识别，Bouc-Wen 模型的参数识别结果如表1 所示。将滞回模型参数归一化，非线性参数识别结果如图2 所示。由表1 可知，在激励未知条件下，改进的UKF 方法能够实现Bouc-Wen模型参数的准确识别，识别误差均低于3.2%。地震荷载和Bouc-Wen 模型滞回曲线的识别结果分别如图3，4 所示。由图3 可知，未知激励的识别结果与真实值基本一致，且相关系数的计算值为0.96，说明未知激励的识别结果具有较高精度。基于该单自由度Bouc-Wen 模型的识别结果可知，在输入未知条件下，本研究所提方法能够准确地实现非线性系统参数和外荷载的同步识别。

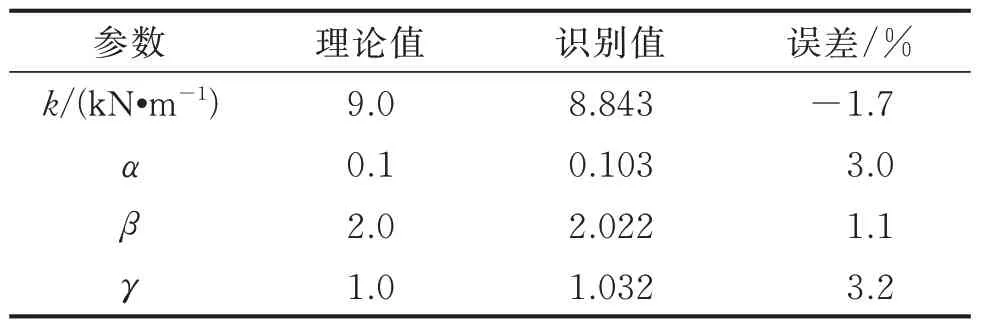
表1 Bouc-Wen 模型的参数识别结果Tab.1 The identified parameters of Bouc-Wen model

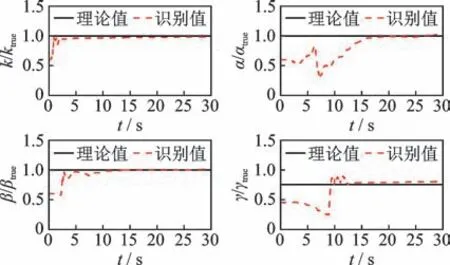
图2 非线性参数识别结果Fig.2 The identified results of nonlinear parameters

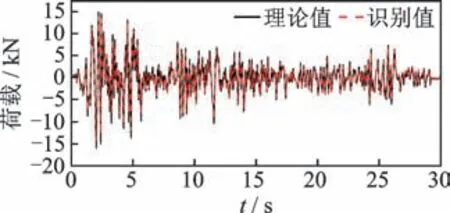
图3 地震荷载识别结果Fig.3 The identified results of unknown seismic loads

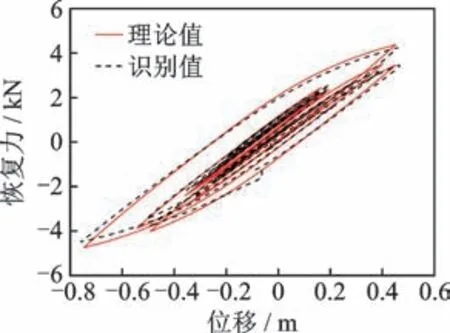
图4 Bouc-Wen 模型滞回曲线识别结果Fig.4 The identified hysteric loop of Bouc-Wen model

为研究观测量对识别结果的影响，分别对2 种工况进行讨论：①仅加速度响应已知；②加速度和位移响应同时已知。利用所提的改进UKF 方法分别对2 种工况下的参数及未知激励进行同步识别，并对比在不同观测量组合下的参数识别结果和荷载识别结果，分别如表2 和图5 所示所示。由表2 可知：在工况1 下非线性参数的最大识别误差为7.7%；当加速度和位移响应同时作为已知观测量时，非线性参数最大识别误差仅为3.2%，识别精度显著高于工况1 的结果。由图5 可知：当仅把加速度响应作为已知观测量时，识别的外部激励在时间序列后半段出现飘移，相关系数计算结果为0.91，这是因为当仅以加速度响应作为观测量时，由于积分误差逐步累积，导致识别过程不稳定；当同时采用加速度和位移响应作为观测量时，识别的外部激励与真实值基本一致，识别精度较高。

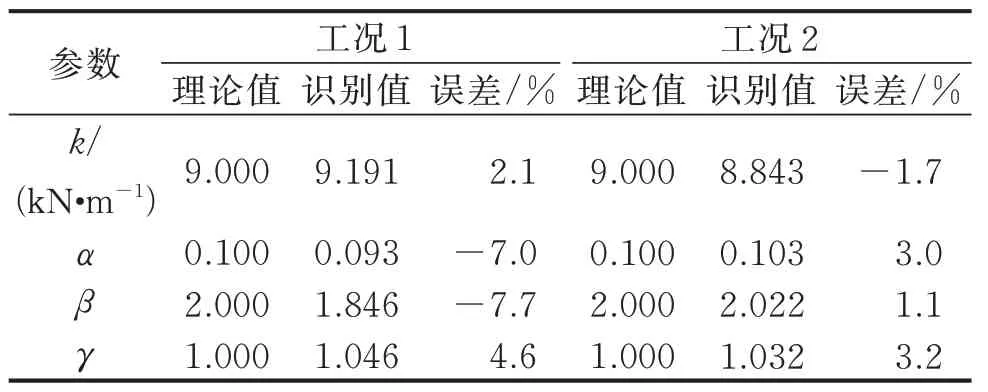
表2 不同观测量组合下的参数识别结果Tab.2 The identified parameters under the different combinations of observations

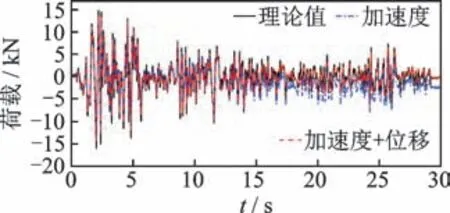
图5 不同观测量组合下的荷载识别结果Fig.5 The identified unknown loads under the different combinations of observations

为了验证测量噪声协方差矩阵的更新对识别结果精确性的影响，笔者以单自由度非线性系统为例，对有/无测量噪声矩阵更新的2 种工况进行计算，其中工况1 为本研究所提出的改进UKF 方法，工况2为不考虑测量噪声协方差矩阵更新。2 种不同工况下的参数及荷载识别结果分别如表3 和图6 所示。由表3 和图6 可知，2 种工况下，非线性参数和输入荷载的识别结果均具有较高的精度。但由相关系数的计算结果可知，当不考虑测量噪声协方差矩阵的实时更新时，相关系数的计算结果为0.93，低于工况1 的计算结果0.96。因此，通过对噪声协方差矩阵进行实时更新，能够提高非线性系统的识别精度。

表3 2 种不同工况下的参数识别结果Tab.3 The identified parameters under the two different cases

图6 2 种不同工况下的荷载识别结果Fig.6 The identified unknown loads under the two different cases

为验证本研究方法在非线性系统和未知荷载同步识别方面的优越性，将识别结果与UKF-UI算法［16］进行了对比。不同算法下非线性参数及荷载识别结果分别如表4 和图7 所示。由结果可知，2 种方法均能实现未知荷载作用下的非线性系统识别，识别值与理论值吻合较好，相关系数均为0.96，但本研究方法的参数识别精度略高于UKFUI 方法。此外，由于UKF-UI 方法采用了迭代最小二乘算法对未知激励进行估计，计算效率相对较低。

表4 不同算法下非线性参数识别结果Tab.4 The identified nonlinear parameters based on the different methods

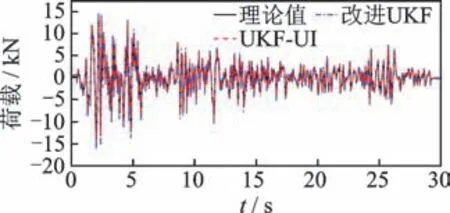
图7 不同算法下荷载识别结果Fig.7 The identified unknown loads based on the different methods

3.2 5 自由度非线性系统

为进一步验证改进UKF 方法对多自由度非线性系统识别的有效性，对某地震激励作用下的5 自由度Bouc-Wen 模型进行数值模拟，5 自由度非线性结构系统如图8 所示。在地震荷载作用下，该非线性系统的运动方程为

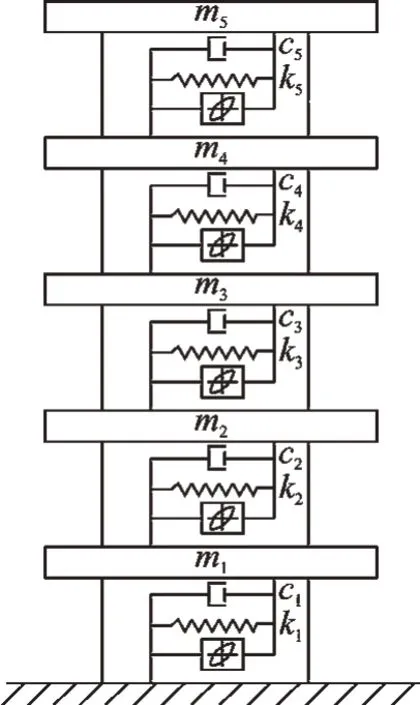
图8 5 自由度非线性结构系统Fig.8 The five degrees of freedom nonlinear structural system

其中：M，C分别为刚度矩阵和阻尼矩阵；R(x，z，t)为系统恢复力；u为外荷载；L为荷载分布向量。

5 层Bouc-Wen 模型设计参数如表5 所示，地震激励选用1940 年的El Centro 地震波，持续时间为30 s，采样频率为50 Hz。

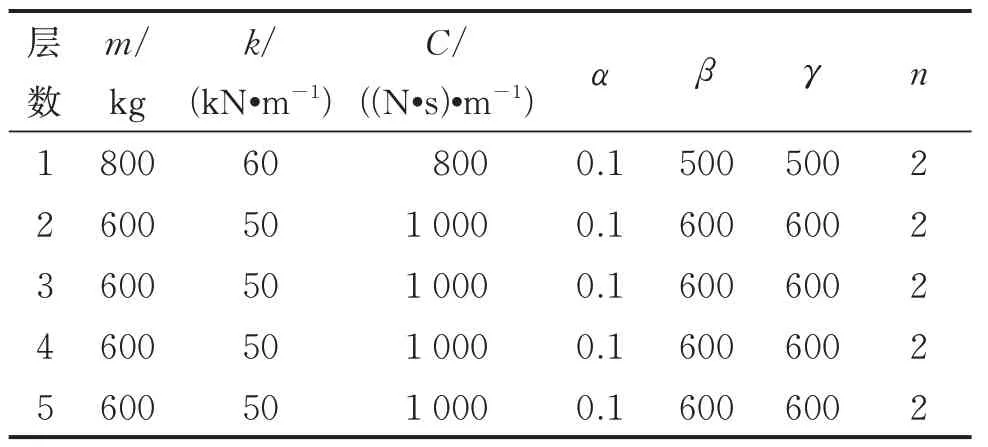
表5 5 层Bouc-Wen 模型设计参数Tab.5 The design parameters of five-storey Bouc-Wen model

将结构各层位移S、速度、滞回位移z、刚度k以及非线性参数α，β，γ写入状态向量，得到系统广义状态向量。该非线性系统和状态空间方程为

其中：A=(α1，α2，α3，α4，α5)T；B=(1-α1，1-α2，1-α3，1-α4，1-α5)T；。

选取各层加速度响应作为观测量，为避免由于积分误差所引起的荷载识别漂移现象，本算例将第4 层位移响应作为已知观测量用于系统识别。此外，为模拟测量噪声对识别结果的影响，分别对已知的加速度和位移响应加入5%的高斯白噪声，并基于改进的UKF 方法对未知激励作用下的非线性系统进行识别。5 自由度非线性模型参数识别结果如表6 所示，底层和第3 层非线性参数识别结果如图9所示，未知荷载识别结果如图10 所示。对比表6 和图9 可知，利用改进的UKF 方法能够精确识别该非线性系统参数，且最大识别误差低于5%。由图10可知，未知荷载识别结果与真实值吻合较好，相关系数为0.98。底层滞回曲线识别结果如图11 所示，由图可知，基于改进的UKF 方法，结构在地震作用下的非线性力学行为能够被准确识别。综上所述，本研究所提出的改进UKF 方法能够对多自由度非线性结构参数和未知激励进行同步识别。

表6 5 自由度非线性模型参数识别结果Tab.6 The identified parameters of the five-DOF nonlinear model

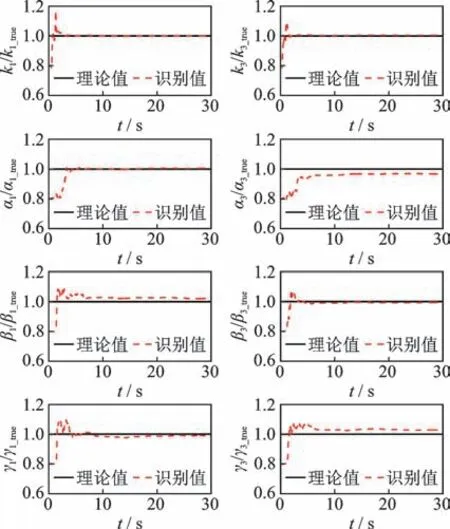
图9 底层和第3 层非线性参数识别结果Fig.9 The identified nonlinear parameters of the 1st and 3rd floors

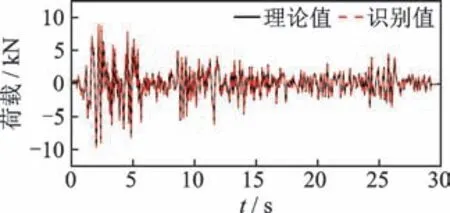
图10 未知荷载识别结果Fig.10 The identified results of unknown loads

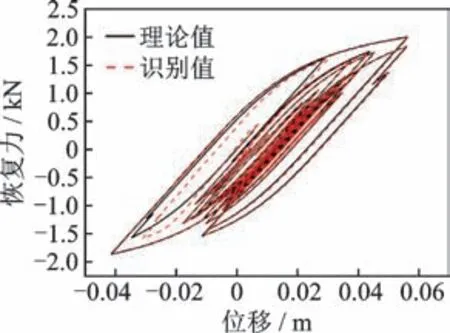
图11 底层滞回曲线识别结果Fig.11 The identified hysteric loop of the 1st floor

4 结束语

提出了一种基于改进UKF 的非线性参数和荷载同步识别方法。该方法在系统状态更新过程中，利用结构响应和参数的当前预测值，对输入荷载进行初步估计，并进一步结合系统状态的估计值对输入荷载进行识别。为降低测量噪声对非线性系统识别结果的影响，在UKF 方法中嵌入卡尔曼滤波器对测量噪声协方差矩阵进行同步优化，确保了非线性结构荷载和参数识别的精确性。为了验证该方法的可行性和准确性，分别对地震激励下的单自由度和5 自由度Bouc-Wen 模型进行数值模拟。模拟结果表明，所提出的改进UKF 方法能够对非线性系统参数进行可靠识别，对随机输入可进行同步估计。此外，由于测量噪声矩阵在系统状态估计过程中被实时更新，因此该方法具有较好的噪声鲁棒性。