偏振光测量之理论溯源及数据处理

梁钰林,邢燕霞

(北京理工大学 物理学院,北京 100081)

在大学物理的理论范畴和实验条件下,偏振光的唯一可观测量是光强分布.顾名思义,线偏振就是一条直线,圆偏振就是圆,椭圆偏振就是椭圆,但实验测量的结果并非如此,所谓“线偏不线,椭偏不椭”,这给初学者造成很大困扰.事实上,偏振光的理论定义和实验观测并不直接相关,人们对偏振光的误解绝大多数均源于此.既然“线偏不线,椭偏不椭”,为何还要叫作线偏振、圆偏振、椭圆偏振光呢?最重要的,理论定义的偏振光应该具有什么样的实验指征?

想要厘清这些问题,必须借助实验观测.但是受课时限制,光的偏振的实验内容简单粗糙,实验部分的基础理论很难在区区3个实验课时内讲清楚,而大学物理课堂理论仅止于线偏振光的马吕斯定律,完全不涉及椭圆偏振光的实验预测.这导致两个后果:1) 学生对椭圆偏振理论的理解似是而非;2) 理论和实验严重脱节.不仅如此,由于实验结果显示“线偏不线,椭偏不椭”,这样的实验测量不仅不能让初学者深入理解偏振现象及其本质,反而带给他们无尽的困扰.相关文献[1-4]大都局限于实验数据处理的细节,没有从理论上追根溯源,从根本上阐明偏振的本质.为了更好地理解偏振理论,澄清偏振光概念上的一些误区,本文做了以下3个工作:1) 从光的偏振的基础理论出发,结合具体的实验现象,对每一步实验现象追根溯源,找到“线偏不线,椭偏不椭”的理论依据;2) 从实测的实验数据出发,清晰地还原椭圆偏振光的椭圆性,找到严谨但容易造成误解的理论定义和直观却不符合直觉的实验现象之间的直接联系,进而直观地展示理论定义和实验现象之间的差别和产生这种差别的根源;3) 通过理论-实验,实验-理论的双循环模式构建偏振理论和实验互通的桥梁.

1 偏振的物理本质

光的频率和波长都可以作为光的量子态指标,二者作用相当.偏振光是具有确定振动姿态的光,除了特定的频率(或波长),偏振光还有一个至关重要的态指标:振动姿态.

根据电磁场理论,光是横向振动光速传播的电磁场,下面用电场E(或者磁场B,二者互相垂直)来表征电磁场.电磁场是协变场,电磁波自然也是谐波,但它不同于一般的谐波.普通谐波的振动方向是固定的,用一个谐振函数即可表示其振动位移,即

l(t)=Aei(ωt-kz)

(1)

而电磁波的振动方向却是任意的,它有两个独立的振动自由度,可以沿垂直于传播方向的x-y平面内的任一方向振动,因此必须用两个独立的振动矢量来表示电磁波的振动. 这两个独立矢量互相垂直,方便起见,定义为x和y方向. 两个方向的振动分量都表示为和普通谐波一样的谐振函数,即[5]

Ex(t)=Axei(ωt),Ey(t)=Ayei(ωt+δ)

(2)

为简便起见,已略掉空间变化,只保留时间相关的相位ωt.

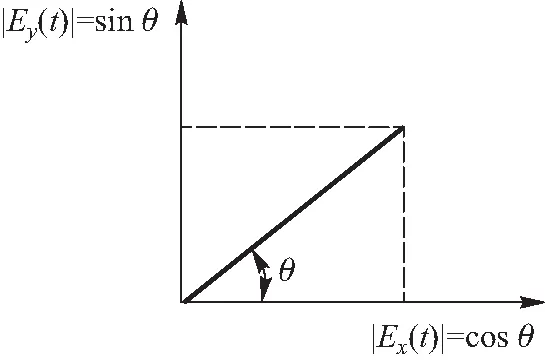
图1 电磁波两个独立振动方向的振幅示意图

为精确描述振动姿态,定义如图2所示的瞬时振动方向α(t),表示振动矢量在t时刻和x轴的夹角,谐振函数取复函数的实部,瞬时振动方向满足

图2 瞬时振动方向

(3)

瞬时方向α(t)不同,振动矢量Ex(t)形成的轨迹也不同. 变量ωt随时间均匀变化,周期平均后和实验测量方位角φ等价.δ=±90°时,有tanα=tanθtanφ.

2 偏振的数学表现

偏振是一种可以精确刻画的确定的振动姿态.振动矢量Ex(t)形成的轨迹可以形象地描述振动姿态,这个振动姿态就是本文所要研究的偏振态.方程(2)中两个方程右边取实部,联立消掉ωt时间参数,即可得到Ex和Ey的隐函数关系[6]为

(4)

这是一个关于Ex和Ey的中心位于原点的椭圆曲线方程,也是瞬时振动矢量的端点在x-y平面形成的运动轨迹. 相位差δ的正负决定矢量端点的运动方向,用于定义左(右)旋光,δ的大小则决定椭圆形状,从而决定偏振矢量的整体振动姿态.

图3展示了δ=0°、30°、60°、90°四种不同偏振态的矢量轨迹.δ=0°时,tan[α(t)]=tanθ,两个方向振动完全同步(同涨同消),合振动方向不变,振动轨迹为直线,为图3(a)所示的线偏振态;δ=90°时,方程(4)退化为长短轴和坐标轴重合的正椭圆方程,此时,x和y方向的振动完全不同步(一涨一消),振动轨迹为正椭圆,为图3(d)所示的正椭圆偏振态,教科书或文献中提到的椭圆偏振通常指这种正椭圆偏振态.

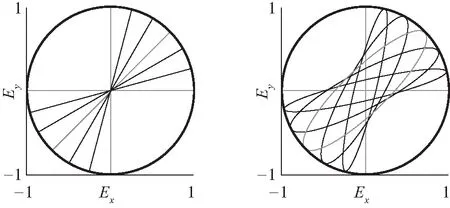
δ=0° δ=30°

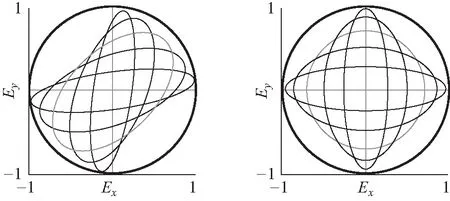
δ=60° δ=90°图3 不同δ下偏振光矢量的振动轨迹,每幅图中的7条曲线代表θ 为0°、15°、30°、45°、60°、75°、90°时的7种混合比例

通常情况下,两个互相垂直且相互独立的振动既不完全同步(同涨同消,δ=0,±180°)也不完全不同步(一涨一消,δ=±90°),其整体振动轨迹为长短轴不在x/y方向的斜椭圆. 图3(b)和图3(c)展示了δ=30°、60°时的一般偏振态的振动轨迹. 为方便描述斜椭圆姿态,定义斜椭圆长短轴方向分别为新坐标系x′和y′方向,x′和x轴的夹角设为β. 通过坐标变换可知,只有当θ=0°、45°、90°时,β=θ. 此时,斜椭圆倾角固定,不随相位差δ改变而改变,这3种特殊的混合比(图3中的深灰和浅灰曲线)正是正椭圆偏振态的特殊情形,即线偏振和圆偏振对应的混合比.

3 偏振的实验指征

偏振具有明显的方向性,空间分布具有强烈的各向异性,光强分布当然也不例外. 但由于电磁场随时间快速变化,比如,波长600 nm的可见光,振动频率达到5×1017Hz,在探测器响应时间尺度下,光矢量的大小和方向瞬息万变,根本无法探测瞬时电场,也无法如电学实验中探测周期电场一样,用示波器探测电磁场的波形图(瞬时矢量信息),只能探测周期平均下的能量(光强)分布. 换句话说,电磁场没有波形图,只有光强分布. 实验上只能通过光强分布来标定偏振态. 那么,不同的偏振态又各自具有什么样的光强分布?

3.1 同步振动的线偏光

线偏振光振动方向保持不变,可看做两个相互垂直的同步振动的合矢量. 如图4所示,合矢量E(t)=Aeiωt,其长度瞬时变化,但方向不变,可通过矢量投影分解到任意两个相互垂直的面内方向,分解后的两个方向的振动相位依然同步,探测任意方向的投影光强即可得到线偏光的光强分布.实验所测光强为放大后的相对光强,其绝对值无意义. 方便起见,依然使用归一化的光强,设线偏振光振动方向为x方向,振幅A=1,探测方向和线偏振光呈φ角,其光强记为Pφ,对归一化的光矢量做矢量投影,Eφ(t)=E(t)cosφ=eiωtcosφ,探测光强Pφ=|Eφ(t)|2=cos2φ,这是大家熟知的马吕斯定律. 如果在垂直方向再放一个探测器P′,则有P′=sin2φ. 相互正交的两个方向等效于两个正交完备基[7],通过这两个方向的探测,可以收集线偏振光所有的能量,满足能量守恒P=P′+Pφ=1.

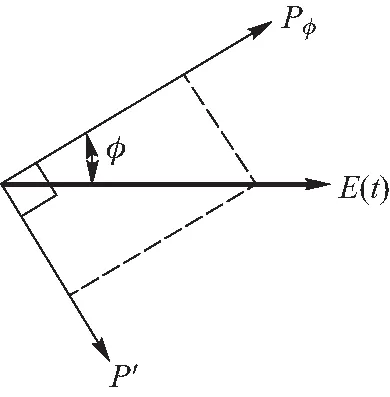
图4 线偏光投影分解测量

图5(a)展示了线偏振光光强随角度的变化.探测方向(深灰色线)只能收集部分光强Pφ=cos2φ,垂直方向P′收集剩下的所有光强(浅灰色线),二者满足Pφ+P′=1. 图5(b)展示了光强和cos2φ的完美线性关系,深灰色直线代表我们熟悉的马吕斯定律. 图5(c)展示了极坐标下光强的角分布. 据此可判定,实验上测到的线偏振光的角分布Pφ(深灰色线)必定为标准的倒“8”字型,而非直线型,所谓“线偏不线”. 因此,线偏振的实验指征绝非“直线”,而是光强为零的消光现象. 光强零点位于倒“8”字的90度方向. 图5(c)的黑色圆圈为深灰色线和浅灰色线的数据之和. 可以看出,沿任意角度(灰色辐射线)分解测量,总光强均保持不变,这是由能量守恒的基本原理决定的.

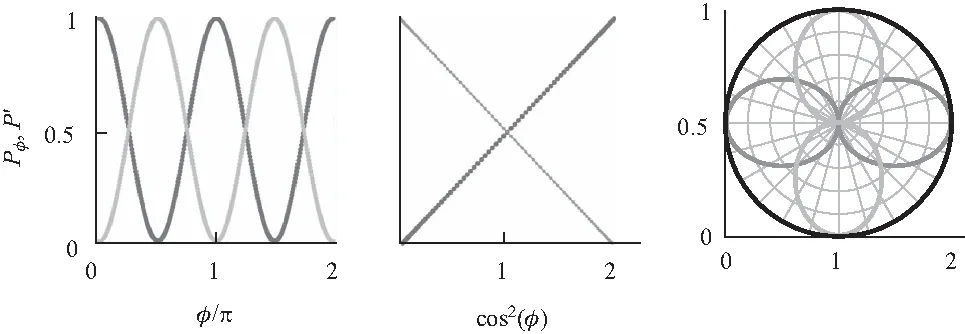
相互垂直的两方向的线偏光光强随φ角的变化 两方向的线偏光光强随cos2φ的线性分布 两方向的线偏光光强在极坐标下的角分布图5 线偏振光的光强分布

3.2 不同步振动的椭圆偏振光

椭圆偏振光由两个线偏振矢量合成,这两个线偏振矢量不同步,存在相位差δ. 由于合振动的矢量方向瞬息万变,无法直接进行矢量投影,如图6所示,要想进行有效的矢量投影,必须把椭圆偏振光还原成两束不同步的线偏振光Ex(t)=cosθeiωt和Ey(t)=sinθei(ωt+δ),再把两束线偏振光分别投影到测量方向(图6深灰色点线所示),分光强相加即可得到这个方向的总光强

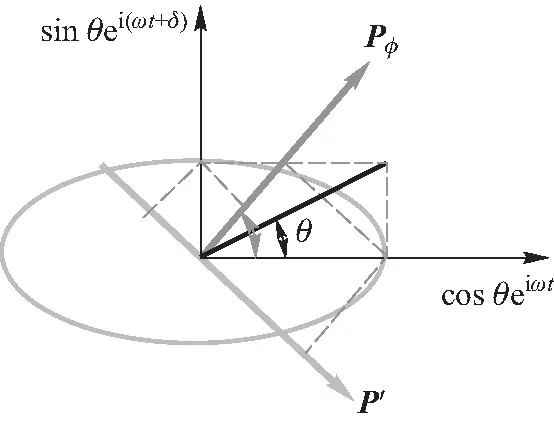
图6 椭圆偏振光投影分解测量.

Pφ=cos2θcos2φ+sin2θsin2φ

(5)

注意,分光强只取决于线偏振光的振幅,和相位无关,表征周期平均后的整体强度. 因此,尽管线偏振光的相位差δ影响振动姿态(斜椭、正椭),但却不影响光强分布Pφ. 这意味着,斜椭圆偏振和正椭圆偏振光的光强分布完全相同,以下只研究正椭圆偏振的光强分布. 无论是线偏振光还是椭圆偏振光,其光强,也就是能量,是确定的,φ方向只能测到部分能量,剩下的能量全部集中在垂直方向(图6的浅灰色箭头),两束线偏振光分别投影亦可得到此方向的光强P′=cos2θsin2φ+sin2θcos2φ,容易验证,Pφ+P′=cos2θ+sin2θ=1,表明总光强和测量角度φ无关,意味着所有的正交完备基地位均等,都可用来合成和分解偏振光.

图7(a)展示了以不同比例矢量合成的椭圆偏振态沿φ方向光强Pφ在极坐标下的角分布. 矢量合成混合比例Ay∶Ax=tanθ,取θ=0°、30°、45°、60°、90°. 从图7(a)可以看出,θ=45°的圆偏振光,其光强分布也是圆形(浅灰色圆圈),因此圆偏振光检测相对容易,实验上也最常用. 与此形成鲜明对比的是θ=0°、90°的线偏振光和θ= 30°、60°的椭圆偏振光,线偏振光的光强分布并非直线(深灰色曲线),椭圆偏振光的光强分布也并非椭圆(黑色曲线),正所谓“线偏不线,椭偏不椭”. 它们的光强分布都是细腰哑铃形,线偏振光细腰宽度为零,椭圆偏振光细腰宽度非零. 椭圆偏振光和线偏振光的唯一区别就在于哑铃细腰宽度是否为零,即是否存在特定角度的消光现象. 相比于线偏振光和圆偏振光,椭圆偏振光的判别并不容易,因此实验上很少用椭圆偏振光. 图7(a)图中的黑色大圆圈代表Pφ和P′之和,表明沿任意角度(灰色辐射线)分解测量,总光强保持不变.

线偏振、椭圆偏振、圆偏振光都是特定的量子叠加态[7],本质上并无区别,都属于线性叠加的量子纯态. 这导致所有偏振光的光强Pφ均呈现如图7(b)所示的与cos2φ成线性关系,表示为Pφ=εcos2φ+(1-ε)/2,其中,斜率ε=1-2sin2θ表征偏振的各向异性程度.ε=0代表各向同性的圆偏振光(浅灰色直线);ε=±1表示完全沿x或y方向振动的极端各向异性的线偏振光(深灰色直线);0<|ε|<1表示各向异性的椭圆偏振光(黑色直线). 我们熟知的马吕斯定律只是这种线性关系的特例(ε=1).

以上考虑的是理想单色波的完全偏振态. 完全偏振态是一个理想的量子纯态,实现完全偏振有两个前提:保证单色,即ω固定;保持相位即δ固定. 两个条件中,第一个单色条件更容易满足,原子发光光谱便具有单色性. 第二个相位保持条件很难实现[8]. 要知道,一个原子一秒钟就能够发射108个相同频率的光子,发光光源中又包含了摩尔数量级的原子,因此在每一次有效测量时间内,都有无穷多个振动姿态各异的光子到达探测器,所看到的探测信号必定是大量光子的集体平均效果,平均的后果完全抹杀偏振态的各向异性的振动姿态.因此,普通光源发出的自然光的光强分布必定各向同性,此谓完全非偏振光. 如果非偏振光叠加偏振光,则为各向异性的部分偏振光.

设线偏振光光强为A,自然光光强B,取线偏振光的振动方向作为角向的零点,二者叠加的总光强Pφ=Acos2φ+B=(A+B)cos2φ+Bsin2φ,这是一个标准的椭圆偏振光的光强分布(方程5).如果A=0,则Pφ完全等同于圆偏振光的光强分布. 因此,单从光强分布无法区分圆偏振光和自然光,也无法区分椭圆偏振光和部分偏振光. 要想区分二者,必须借助偏振光的特性,即它的纯态特性.组成纯态的量子叠加态有确定的相位,因此偏振态的相位(δ)有迹可循,总可以通过相位补偿把所有的偏振光都变为线偏振光,而线偏振光是极端各向异性光,在垂直方向可以完全消光. 部分偏振光和自然光则没有确定的相位,无法进行相位追踪,也无法通过相位补偿使之变为线偏振光,因此无论如何也做不到特殊角度消光. 综上,光强分布结合消光操作即可通过简单的光强测量确定偏振态.

4 偏振的实验测量

本小节将通过实测数据验证前面的理论预测,并根据前面的理论推导,利用实测数据还原偏振光矢量的振动轨迹. 实验仪器如图8所示,包括光源、光学元件(含两个偏振片和一个1/4波片)、光功率测量仪(含接收器和指示器),所有仪器均置于光具座上,以保证光路准直.

图8 实验仪器实物

实验所用光源为毫瓦级半导体激光. 高质量的激光器可以同步大量原子的量子态[8],产生振动方向确定的线偏振光. 但椭圆偏振光无法直接从光源获得,必须利用波片制造椭圆偏振光. 波片是折射率各向异性的二相色散晶体切片,切片法线沿着各向异性最大的方向. 如图9所示,线偏振光垂直入射波片,出射光线变为两束振动方向互相垂直的同方向传播的线偏振光. 由于折射率不同,两束线偏振光速一快一慢,在晶体中产生固定相位差,相位差正比于晶体厚度d,1/4波片产生δ=π/2(+2nπ)的相位差. 两束振动方向垂直、相位差δ=π/2的线偏振光叠加合成正椭圆偏振光. 鉴于现有的测量条件(只测光强)无法区分斜椭圆偏振和正椭圆偏振,下面只测量并分析相位差δ=±π/2的正椭圆偏振的实验数据.

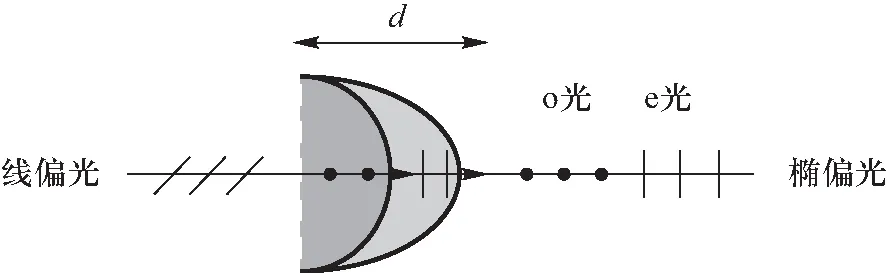
图9 利用波片产生椭圆偏振光原理示意图

大学物理实验所用激光器无法保证线偏振光的偏振度,还需让激光透过偏振片,产生理想的线偏振光. 如图10所示,部分偏振的激光透过透光方向为M的偏振片(起偏器),变为理想的线偏振光P0,振动方向平行于M. 此线偏振光为后续所有实验测量的唯一光源,具有确定的光强和偏振方向.为便于和理论结果进行比较,对此线偏振光强进行归一化,即设P0=1,并设它的振动方向M为x方向. 波片有两个透光方向(短划线),分别为o光和e光的振动方向,这两个方向正是构成椭圆偏振光的两个线偏振光的振动方向. 为了定位这两个振动方向,必须借助偏振片,如图10所示,两个透光方向相互垂直的偏振片定义一对正交基,在不插入波片的情况下,透光为零,是为一次消光,之后,在两个偏振片之间插入波片,由于透过波片的两束线偏振光无法同时和检偏器透光方向垂直,消光解除,此时的透光为椭圆偏振光. 但是有一种情况例外,那就是当波片的o光和e光的振动方向分别平行于起偏器和检偏器的两个透光方向时,M方向偏振光可以完全透过波片,但是完全无法透过具有垂直透光方向的检偏器,是为二次消光. 此时,M和N就是o光和e光的振动方向. 转动波片,即可得到各种姿态的偏振光,转动检偏器(透光方向N),可测量各种偏振光的光强分布Pφ.

图10 椭圆偏振光测量原理图

如图11所示,椭圆偏振光的轨迹椭圆的长短轴沿转动的o光和e光方向,椭圆的形状取决于两束线偏振光振幅的相对比例Ae/o/Ao/e=tanθ,其中,θ为波片转角,定义二次消光的位置为θ=0. 图11(a)、11(b)分别展示了θ<45°和θ>45°的两种不同的振动姿态. 如前所述,θ=0°、90°为线偏振光,θ=45°为圆偏振光,其余情况为椭圆偏振光.

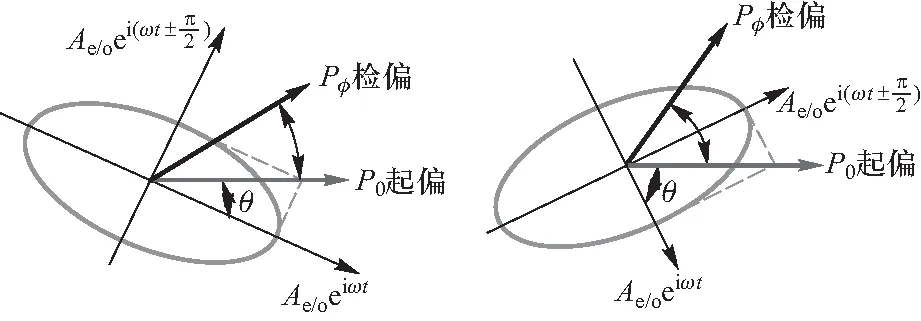
θ<45° θ>45°图11 椭圆偏振光测量角度示意图

图12展示了θ=0°、30°、45°、60°、90°五种混合比例下的椭圆偏振光强分布Pφ.图12(a)中,φ角的零点定在x轴方向,即起偏方向. 为便于和理论结果进行比较,图12(b)把φ角的零点变为跟随波片转动的移动零点,此零点固定在波片的o/e光的振动方向. 图12的光强分布显示,不管φ角如何变,总光强Pφ+P′基本保持不变(最外层的大圆),意味着能量守恒已满足,光强无损耗,测量数据基本可靠. 图中三角标记的曲线为线偏振,实心点标记的曲线为椭圆偏振,圆圈标记的曲线为圆偏振,线偏振、椭圆偏振和圆偏振光强分布分别为“8”字形、细腰哑铃形和近似圆形,和理论分析基本一致.

角坐标零点固定的极坐标系下 角坐标零点随波片移动的极坐标系下图12 不同坐标系下线偏振、椭圆偏振、圆偏振光的光强角分布

为了进一步验证实验测量的可靠性,根据振动方向α和测量方位角φ的关系tanα=tanθtanφ,图13还原了图12的光强分布对应的光矢量端点轨迹图,轨迹图清晰地呈现了线偏振的线性轨迹和椭圆偏振的椭圆轨迹,直观地呈现出各种偏振光的振动姿态,从实验的角度形象地解释了线偏振和椭圆偏振的由来.

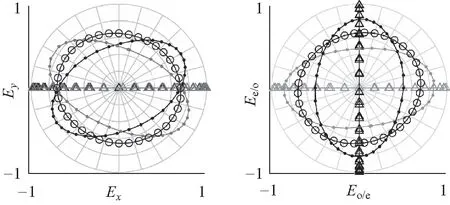
图13 利用图12中的光强数据还原对应的振动矢量端点轨迹图

5 测量误差分析

理论上,圆偏振光的光强分布和矢量轨迹都是理想的圆形,但图12和13中的圆圈标记曲线并非圆形,尤其是光强分布图,更像是倾斜的长椭圆.椭圆偏振的椭圆也有少许形变扭曲. 这意味着,实际测量中波片两个振动方向的透光率并不完全相同,这种现象在偏振实验测量中经常出现,非常具有代表性. 初步分析,原因如下.由于激光光斑较大,实际实验中在光路并未完全准直的条件下,接收器依旧可以接收到毫瓦级的正常强度的光强,因此造成线斜入射垂直放置的波片而实验者并未察觉的情况. 由于斜入射的线偏振光的振动面和波片所在平面不垂直,因此无论波片如何转动,线偏振光也无法完全透过波片. 极端情况,波片的一个振动方向,例如Eo,正好位于线偏振光的振动面内,透过率最不完全,影响最大. 此时,Ee方向完全不受影响,依然保持零透光.一般情况,两个方向都有影响,但影响程度不同,实验中波片振动方向随机(摆放),因此便造成如图13所示的无规倾斜的长椭圆式的圆偏振轨迹,以及轻微扭曲的椭圆偏振轨迹.

此外,整个实验仪器设备粗糙简陋,也会造成实验数据偏离理论值的情况. 图14展示了θ=0°、30°、45°、60°、90°五种混合比例下偏振光强Pφ随cos2变化的线性曲线. 其中,实线为理论曲线,同图7右图,圆点为实测数据,深灰色、黑色、浅灰色分别为线偏振、椭圆偏振、圆偏振光的结果.理论曲线呈现完美的线性关系(直线),但实测数据并非理想的线性曲线,数据的线性回归相关系数r<1. 可以看出,线偏振光(各向异性度最高)的线性程度最高,圆偏振光(各向同性,椭圆偏振度最低)线性程度最低,这说明波片使用中更容易出现问题.

图14 实验数据的线性和椭圆偏振度示意图

6 结论

本文利用大学物理实验室的简单光学仪器构建并探测各种偏振光. 用大学物理的基本知识,溯源偏振光的理论起源、数学表现和实验指征. 用详尽的偏振理论注解实验现象,解释实验上的“线偏不线,椭偏不椭”的怪现象. 以实验数据为唯一依据,还原线偏振的线振动和椭圆偏振的椭圆轨迹,以能量守恒为基本准则,验证实验数据的可靠性. 以理论推导为桥梁,找到唯象的理论定义和反直觉的实验现象之间的关联,帮助初学者更好地理解光偏振现象的本质.