浅谈变分原理及其一些应用

郑神州,于海燕

(1. 北京交通大学 数学与统计学院,北京 100044; 2.内蒙古民族大学 数理学院,内蒙古 通辽 028043)

变分技术有着悠久的历史,几乎与微积分理论同时诞生. 变分法是从约翰·伯努利(1696年)提出最速曲线问题开始出现的,同时代的牛顿和莱布尼茨对该发展也有贡献. 历史上,欧拉对这个理论的贡献非常大,他的著作《变分原理》给予了这门科学这个名字,当今人们把对应于泛函的临界点的微分方程称为欧拉方程,或称欧拉-拉格朗日方程. Weierstrass给出的反例表明:通常连续的可微函数空间可能达不到泛函的极值,他的贡献完善了变分学,使其具备现代表述特征. 20世纪伊始,希尔伯特在巴黎国际数学家大会的讲演中提到的23个著名数学问题就涉及变分问题,变分法的思想贯穿了库朗和希尔伯特所著的《数学物理方法》一书,Pontryagin、Rockafellar和Clarke广义变分法理想控制论发展了新的数学工具[1,2].极小曲面(肥皂泡)研究(又称Plateau问题),拉格朗日力学、最小作用量原理、微分几何中的测地线等均是有约束的变分问题研究[3,4]. 变分是研究泛函的极值问题的基本方法,这是一种处理数学、物理、工程等领域有关最优化问题的一种基本的数学技术,它往往与给定边界条件的某类微分方程(从所周知的欧拉-拉格朗日方程)密切相关[4,5]. 事实上,在物理和工程等实际问题中,经常考虑某个泛函取得极大或极小值(或者是一些约束条件下的极值),变分法就成为处理泛函的数学领域的“微积分”了,和处理函数的普通微积分相对应;所以变分法在泛函问题中所起的作用,犹如微分在函数研究中一样[5,6]. 另外,变分的直接方法来计算近似解,如Ritz法和有限元素法,变分法提供了有限元方法的数学基础;在寻找变分泛函极大和极小值时,在一个解附近的微小变化的分析给出一个近似[6-8]. 很多时候将泛函转化为欧拉-拉格朗日方程,有一些微分方程求解工作可以利用,比如格林函数求解法[3,6,9].

变分技术是物理学和自然界存在方式和运行机制的基本原理[3,6-8]. 例如:几何光学中的费马原理(1662年,又名“最短时间原理”):费马原理正确的称谓应是“平稳时间原理”:光沿着所需时间为平稳的路径传播,光线传播的路径是需时最少的方式.从费马原理可导出3个几何光学定律:光线在真空中的直线传播、光的反射定律和光的折射定律;力学中的最小作用量原理和哈密尔顿原理,等周问题,电磁理论,及量子力学;根据斯蒂芬·沃尔夫冈的说法,爱因斯坦场方程也涉及一个变分原理,作为爱因斯坦-希尔伯特作用量的约束.

1 变分原理

引理1.2(变分原理):如果函数f(x)∈C(a,b),对于[a,b]上满足η(a)=η(b)=0的任意连续函数η(x)(下文中用C0[a,b]表示在[a,b]上紧支的连续函数类),如果

(1)

那么必有f(x)≡0,∀x∈(a,b).

证明:反证法,设有x0∈(a,b)使得f(x0)≠0,不妨设f(x0)>0.由f(x)∈C[a,b],则一定存在ε>0,使f(x)>0,x∈[x0-ε,x0+ε]⊂(a,b)这样我们构造下面一个连续函数η(x):

(2)

其中α=x0-ε,β=x0+ε,所以η(x)∈C0[a,b],且

(3)

与引理1.2条件矛盾,所以对于任意的x∈(a,b),都有f(x)≡0.

推广到高维情形,陈述如下:

引理1.3:设定义在Ω⊂Rn(n≥2)上的连续函数f(x),如果对于在Ω上连续且在∂Ω为零处的任意函数η(x),均有

则f(x)≡0,∀x∈Ω.

定义1.4:如果泛函J[y]在y=y0(x)扰动的一个ε邻域内都不大(小)于J[y0],那么我们称泛函J[y]在y=y0(x)有极大(小)值.也就是说

J[y]≥J[y0](极小),J[y]≤J[y0](极大)

(4)

使J[y]取到极值的函数称为极值函数.

计算泛函J[v]临界函数y=u(x)的欧拉-拉格朗日方程可以通过这样来得到:内积

例1.5:以最简单的泛函为例,讨论使泛函取到极值的必要条件.设

(5)

在α=0达到极值.根据微积分理论得:α=0一定是J(α)的驻点,即

(6)

称之为上述泛函变分问题的欧拉-拉格朗日方程.对于特殊情况:F(x,y′)与y无关时,利用上述欧拉-拉格朗日方程(6),得到

所以

(7)

如计算J[v]临界点时,我们也可以用η=δu来计算δJ[v].

定义1.6:一般地在允许函数类的两个函数y(x)、m(x),若彼此任意接近,那么m(x)与y(x)之差δy(x)=m(x)-y(x)称为函数y(x)的变分.对于一个泛函J[y],函数变分所引起的泛函增加量为ΔJ=J[y+δy]-J[y].如果可以展开为

其中δJ:=L[y,δy]称为泛函的一阶变分,δ2J:=Q[y,δy]为泛函的两阶变分.

这样可得到下面的泛函极值的必要条件.

定理1.7:若泛函J[y]在y=y0(x)上达到极值,则泛函在y=y0(x)上的一阶变分δJ满足

δJ=0

注1.8:当然像函数的驻点不是极值点一样,不是每一个临界点都能达到泛函的极值的,其中鞍点和许多的退化点也是临界点.例如对泛函式(5),计算得到

2 一些典型的应用

欣赏如下几个实际的具体例子,这些例子在相应学科发展史上也起过关键的作用,它们也是理解变分法基本原理、结构和方法的良好途径.

例2.1:最短线(或称短程线)问题:众所周知,连接两固定点的所有连续曲线中最短路径是直线段,这是显然的事实,可要从数学严格意义下得到并不容易.以平面问题为例论证.

图1 最短线问题

(8)

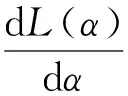
(9)

把式(8)代入式(9),展开后有

(10)

由于式(10)对于任意的η=η(x)都成立,根据变分引理,得到

(11)

求解之,这意味y=C1x+C2.因此,在平面上过固定两点距离最近的光滑曲线是直线.

注2.2:几何光学问题:费马原理表明光线在光学介质中的传播会选择传播时间最短的方式.在非均匀的平面介质中光的速度c(x,y)是随点的变化而变化,与介质的光学性质有关.假设光线传播的轨迹为曲线y=u(x),t为时间变量; 则

(12)

积分之,于是关于曲线u(x)的时间泛函为

(13)

这时,费马原理转化为:寻找连续可导函数y=u(x),使得达到min(T[u]).如果是在均匀介质(如真空)中传播,这时c(x,y)=c是常数;例2.1表明此时的传播路径是直线.

注2.3:曲面上测地线问题:欧式空间R3中曲面S可用函数z=F(x,y)的图[x,y,F(x,y)]表示,在曲面S上寻找连接给定两点M[a1,b1,F(a1,b1)],N[a2,b2,F(a2,b2)]的最短曲线C⊂S,称为其测地线.设曲线C以x为参数表示:x=x,y=u(x),z=F[x,u(x)].于是我们所寻找的测地线是满足边界条件:u(a1)=b1,u(a2)=b2的如下泛函极小值:

(14)

(15)

u(0)=P1,u(1)=P2

连接弧长P1P2的弧长为

(16)

其中c是一个积分常数,由定义知: -1≤c<1.所以

即cθ′2=cos4θ-c2cos2θφ′(t)2,作变量代换t=tanθ,有

例2.5:最速降线问题:在重力作用下,一个粒子沿着该路径可以在最短时间从给定点A到达不直接在它底下的给定点B,如图2所示.

解:先在该竖直平面上取一直角坐标系,以A为坐标原点,水平为x轴,向下为y轴.曲线的方程为y=y(x),A点坐标(x0,y0)=(0,0),B点坐标(x1,y1).曲线上任意一点P时的速度为

因此,重物沿该曲线从A点滑到B点所需要的总时间为

(17)

由于y(0)=0, 所以d=0.于是最速降曲线是一族经过原点的一段摆线(旋轮线)

即:圆周x2+(y-r)2=r2沿x轴滚动时,圆周上点(0,0)的运动轨迹.

注2.6:对于旋转极小曲面泛函式(16),有

则有

由于

得

(18)

这是一条悬链线,常数c、c1由边界条件给出.若取特定常数,得到该参数曲线为旋轮线(或称为摆线)

即:圆周x2+(y-r)2=r2沿x轴滚动时,圆周上点(0,0)的运动轨迹.

例2.7:等周问题:用参数表示的平面曲线方程为x=x(s),y=y(s),参数s可以理解为曲线从起点的长度.如果曲线的长度为l,那么s∈[0,l].由于曲线是封闭,所以有边界条件

x(0)=x(l),y(0)=y(l)

(19)

而该曲线的长度为

(20)

该曲线所围成的面积为(根据Green公式)

(21)