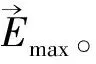部分偏振光分解的研究①
2020-03-11李向阳幺周石陈安和
李向阳,幺周石,贺 腾,李 帅,陈安和
(中国空间技术研究院西安分院,西安 710000)
0 引言
随着科学技术的发展,光学偏振广泛的应用于军事领域和我们日常生活当中。在军事方面,光波从介质界面反射时会产生部分偏振光,目标物、背景物和伪装物反射光的偏振度差别较大,所以军事上采用红外偏振成像技术来识别目标,此外,有线光通信、空间光通信也涉及了偏振光的传输[1]。在民用方面,除了我们熟知的3D电影外,现阶段对光学系统偏振像差的研究与校准也取得了一定的进展。
光波的偏振态有三类:完全偏振光、自然光和部分偏振光,完全偏振光的空间电场矢量随时间按一定规律在振动,而自然光和部分偏振光电场矢量没有一定的规律。其中完全偏振光包括线偏振光、圆偏振光和椭圆偏振光,并且部分偏振态是自然界光波存在的最常见的状态。对于偏振光的数学描述有Jones矩阵、相干矩阵和Stokes矩阵,三种矩阵都可以描述完全偏振光、且形式明确,但是Jones矩阵不能描述自然光和部分偏振光,并且光学教程中对部分偏振光的描述非常含糊[2]。采用相干矩阵和Stokes矩阵描述部分偏振光时,只是指出部分偏振光可以分解成完全偏振光和自然光两部分,并未给出部分偏振光的具体表达,也没有给出在已知部分偏振光两正交成分Emax和Emin的条件下如何分解部分偏振光,及分解前后部分偏振光偏振度求解公式之间的关系。鉴于此,本文主要研究部分偏振光的分解。
1 部分偏振光相干矩阵的分解
相干矩阵是一个2×2的矩阵,其不仅可以描述完全偏振光,也可以描述自然光和部分偏振光[3]。如果光波沿Z轴传播,其电场矢量在x方向的振幅分量为ax,在y方向的振幅分量ay,相位差φy-φx为δ,则此光波的相干矩阵为(1)式:
(1)
对于完全偏振光,两正交方向的振幅分量ax、ay及相位差δ是确定的,将其带入(1)式可以得到完全偏振光的相干矩阵。对于自然光,相邻电场矢量之间没有确定的相位关系,且两正交方向光强相等都为总光强I0的一半,其相干矩阵如(2)式示:
(2)
如图1示,部分偏振光光矢量沿y′方向占优势,其光强用Imax表示,在其正交的x′方向光矢量处于劣势,光强用Imin表示,并且x′oy′坐标系相对于xoy坐标系沿逆时钟旋转了θ角,这样使所要研究的部分偏振光具有一般性。
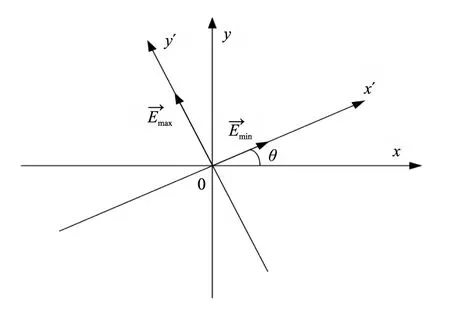
图1 部分偏振光电场矢量描述
(3)
由上述对部分偏振光的分解可知,线偏振光的相干矩阵中ax=ΔI1/2sinθ,ay=ΔI1/2cosθ,δ=π,此处设ΔI=Imax-Imin,则部分偏振光分解后的线偏振光相干矩阵为(4)式。
(4)
采用偏振光的叠加理论可知,部分偏振光的相干矩阵为(5)式。
(5)
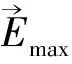
(6)
2 部分偏振光斯托克斯矢量的分解
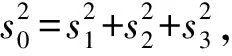
(7)
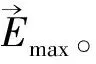
(8)
由上述对部分偏振光的分解可知,线偏振光在 轴方向的振幅为ax=ΔI1/2sinθ,在y轴方向的振幅为ay=ΔI1/2cosθ,相位差δ=π,此处设ΔI=Imax-Imin,则部分偏振光分解后线偏振光成分的斯托克斯矩阵为(9)式。
(9)
采用偏振光的叠加原理可知,部分偏振光的斯托克斯矩阵为S4:
(10)
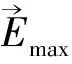
(11)
3 部分偏振光的偏振度
偏振度是描述光波偏振化程度的物理量,其严格定义为“部分偏振光的总光强中完全偏振光所占的百分比”[4],表达式如(12)式:
(12)
由光波的偏振态描述可知,不同表达形式的偏振光其偏振度的求解公式是不相同的,但是对于一束偏振光采用不同的形式描述、或是不同的方法分解,其所描述光波的偏振态应该是相同的,偏振度的求解公式也是相等的。为了进一步验证本文对部分偏振光分解的正确性,此处对不同表达形式的部分偏振光分解前后的偏振度进行了研究。
在光学教程中定义光波偏振度的公式如(13)式示。其中,两正交分量中光强的最大值为Imax,光强的最小值为Imin。
(13)
采用(13)式来求解光波的偏振度存在明显的缺陷,由此公式可知,圆偏振光和自然光的偏振度P=0,部分偏振光和椭圆偏振光的偏振度0 (14) (15) 上述公式(14),(15)可以描述自然光,部分偏振光和完全偏振光,对于自然光P=0,对于部分偏振光0 (5)式是相干矩阵描述的部分偏振光,采用公式(14)可知如下。 (16) (10)式是斯托克斯矢量描述的部分偏振光,采用公式(15)可知如下。 (17) 上述(16),(17)式是在已知部分偏振光Imax,Imin的条件下,由部分偏振光的分解思想,分别采用相干矩阵和stokes矢量描述部分偏振光时的偏振度。由上述结果可知,验证了部分偏振光分解思想的正确性,得到了采用相干矩阵和stokes矢量描述分解后部分偏振光的偏振度,及部分偏振光分解前后偏振度相等的结论。 本文在已知部分偏振光Imax,Imin的条件下,由部分偏振光分解的思想,通过分解前后部分偏振光偏振度的分析,得到如下结论: (II)通过偏振光分解和叠加的思想,从而将一个现实存在的复杂问题简单化,并得到了部分偏振光相干矩阵和斯托克斯矩阵的具体表达,分别如(5)式和(10)式可知,从而便于一般偏振光学一般问题的解决。 (III)通过对部分偏振光的偏振度计算分析可知,光学教程上定义偏振度公式P=(Imax-Imin)/(Imax+Imin)虽然不适用于完全偏振光,但对于部分偏振光此公式和由“总光强中完全偏振光所占的百分比”计算得到的偏振度是相等的,也验证了部分偏振光分解的正确性。4 结论