铁磁共振实验中频散效应的讨论

陈 森,祝邦恺,裴艺丽,李 莉,冉玉晶,吴 平

(1. 北京科技大学 自然科学基础实验中心,北京 100083;2. 北京科技大学 数理学院,北京 100083)

铁磁共振(Ferromagnetic Resonance,FMR)的研究对象是组成铁磁物质原子中的未耦合电子,外部磁场使得磁矩围绕磁场方向发生进动,并受到附加的微波旋转场的影响[1]. 它是铁磁物质的电子自旋的一种反映. 因此,铁磁共振的研究对于物质精细结构以及电子自旋的深入理解具有重要意义[2,3].

许多高校在近代物理实验教学中都开设了铁磁共振的相关课程,实验主要测量参数包含共振频率、共振磁场强度和共振线宽. 共振频率和共振磁场强度可以计算材料的磁旋比和朗德因子,给出材料微观结构的信息[4-6]. 共振线宽是反映磁矩进动过程中所受阻尼的宏观物理量. 在工程上,共振线宽关系到器件的正向损耗和工作带宽,其研究对提高微波铁氧体器件的性能有重要的应用价值[7,8]. 实验中,通过测量谐振腔输出功率与外加恒定磁场H0的关系曲线得出共振线宽[9],通常认为理想的曲线为一等高对称曲线,如图1所示. 然而,该曲线受频散效应的影响,实际测量中往往得到反常的不对称曲线,如图2所示,会导致半共振点的选取不准确,进而带来共振线宽的测量误差. 本文拟从理论上分析铁磁共振实验中频散效应的来源及其对铁磁共振曲线的影响,解决教学过程中的难点.

图1 理想的P出-H曲线

图2 反常P出-H曲线

1 共振线宽

将铁磁材料置于恒定磁场H0中,其中的磁矩M将绕H0做拉莫进动,其进动角频率为

(1)

如果同时在垂直H0的方向加入一个微波旋转场H,当H的旋转方向与进动方向一致且其频率ω′=ω0时,铁磁体会剧烈吸收微波能量,即发生铁磁共振现象,吸收功率与恒定磁场H0的关系曲线如图3所示,其中半共振点(能量吸收为共振吸收一半的位置)间距即为共振线宽ΔH. 铁氧体在微波磁场H与恒定磁场H0的共同作用下,磁矩运动通常用经典的唯象Landau-Lifshitz-Gilbert (LLG)方程来模拟[10],即

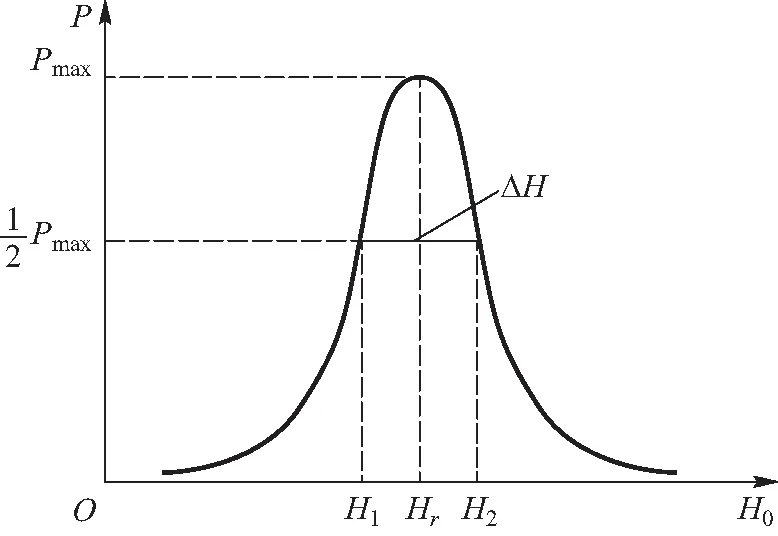
图3 吸收功率P与恒定磁场H0的关系曲线

(2)

其中,α是衡量损耗大小的无量纲的比例系数,称为铁氧体的唯象阻尼系数. 式(2)中右边第一项为进动力矩,第二项为阻尼力矩.Heff为有效磁场,且有

Heff=H+H0

(3)

在线性近似下,由式(1)、(2)、(3)可得

(4)

因此,可以用ΔH表示铁氧体损耗的大小.

2 实验方法

实验采用传输式谐振腔测量共振线宽ΔH,实验系统如图4所示,三厘米固态信号源与TE10p型矩形谐振腔提供频率一定的微波旋转场,微波谐振腔的谐振频率为8 992 MHz,只有工作在这个频率下才能形成稳定的驻波与功率输出. 对于不是谐振频率的其他频率,不存在有效解,此时谐振腔失谐,微波被耦合片全反射,谐振腔内有效场Heff为零. 实验中将样品微波铁氧体(YIG)小球加载在矩形谐振腔磁场最大、电场最小的位置(认为小球足够小,对谐振腔的电磁场分布几乎无影响),固定微波旋转场的频率,改变恒定磁场H0大小,可测得谐振腔输出功率与恒定磁场的关系曲线,即铁磁共振曲线,如图5所示,可以计算出共振线宽ΔH.

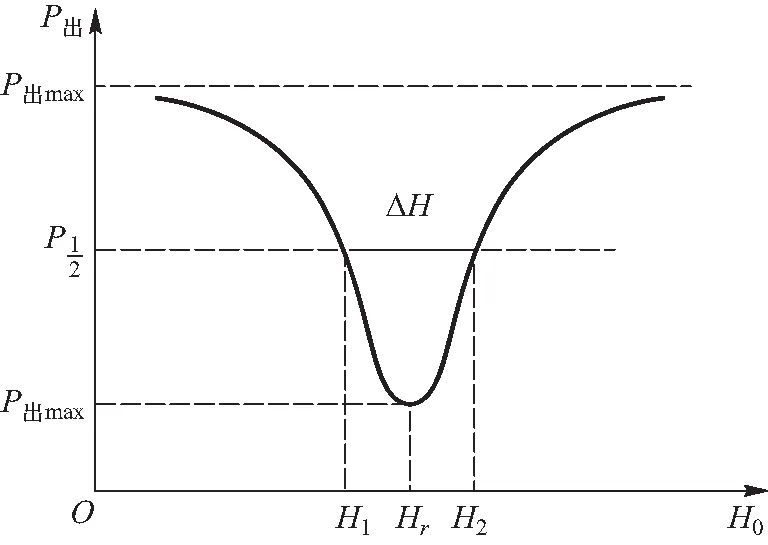
图5 输出功率P出与恒定磁场H0的关系曲线

3 频散效应

由于谐振腔中的外加磁场以及腔体形状会导致待测样品磁导率的变化,进而引起谐振频率ω的偏移[11],随着这种偏移的发生会出现共振波形失真的现象. 从广义来讲,凡是随频率或波长而变化的物理量,都可称为“频散”或“色散”,因此称这种由频率改变而引起的波形失真为频散效应.

实验时,为了简化测量过程,一般采用非逐点调谐法,图6给出了微波旋转场为8 976、8 982、8 986、8 987、8 995、8 997、8 999、9 001 MHz时的铁磁共振实验曲线,其中检波电流I与微波输出功率P出成正比. 由图6可以看出,在微波谐振腔的谐振频率8 992 MHz附近,当微波旋转场频率小于谐振频率时曲线呈现左低右高,当旋转场频率大于谐振频率时曲线呈现左高右低,频散效应明显.

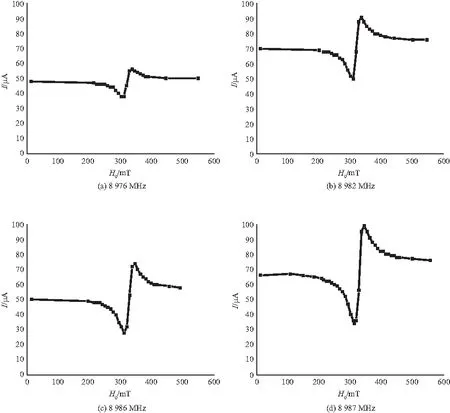
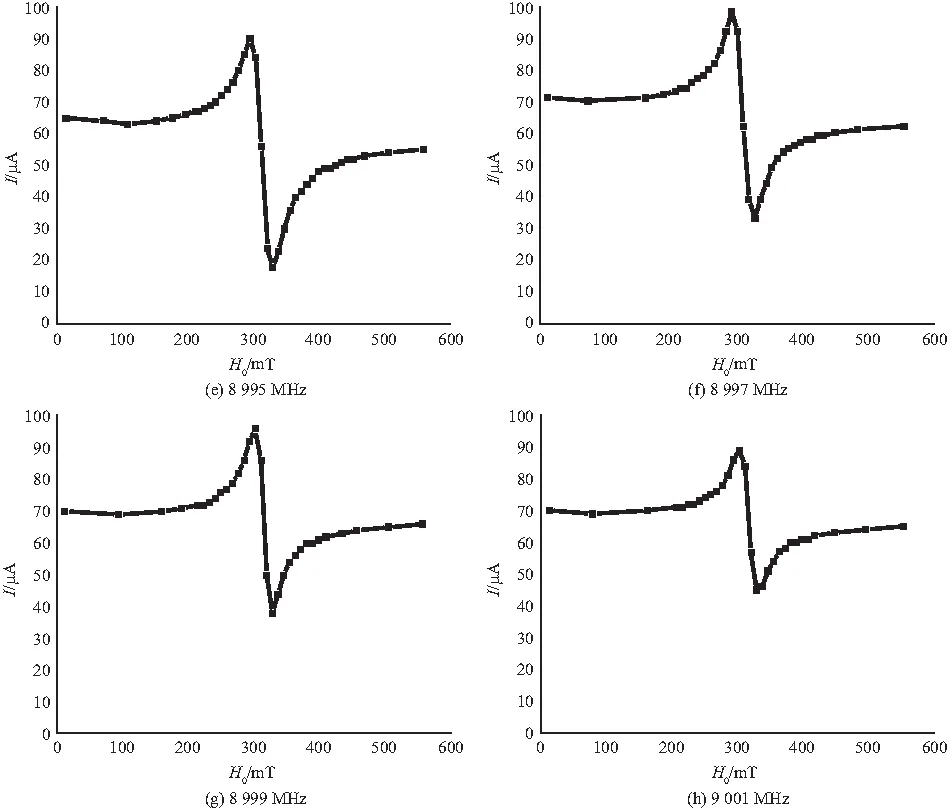
图6 不同微波频率下的铁磁共振曲线

采用逐点调谐方法,电流步长0.05 A,同时调节微波源使微波频率与谐振腔谐振频率一致,测量数据如表1所示,图7给出了逐点调谐的铁磁共振实验曲线,由图7可以看出,曲线两边等高,但不对称,频散效应相对减弱.

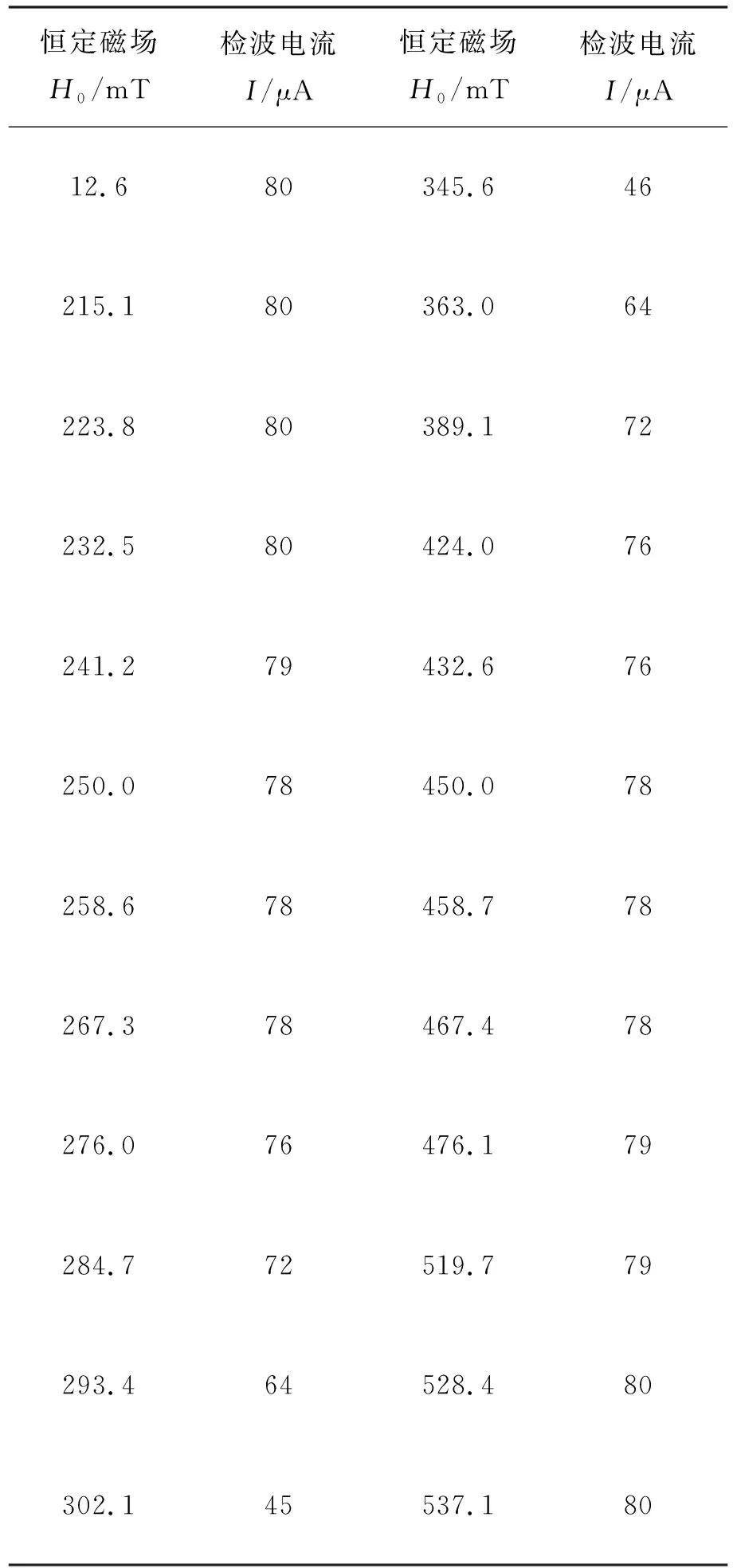
表1 检波电流随恒定磁场大小的变化

4 分析与讨论

对于铁磁共振测量共振线宽时出现的频散效应,许多文献从磁感应强度的角度分析该效应,采用求解铁磁体小球的布洛赫方程组的方式[11,12],引入样品小球磁化强度矢量的两个分量,即吸收信号与频散信号. 当共振频率与微波旋转场频率相等时,样品的磁感应强度与微波旋转场同相位,其吸收信号最强而频散信号最弱,共振曲线为吸收曲线. 当共振频率与微波旋转场频率不相等时,共振曲线为吸收曲线与频散曲线的叠加,曲线出现左高右低或左低右高现象. 该方法认为样品的磁感应强度与样品处的微波旋转场之间存在一定的相位差,导致能量无法被充分吸收,进而形成频散效应[13].

微扰法的基本思想是处理某些系统的物理问题时,如果系统的物理条件只发生微小的变化,那么系统的某种物理量的变化也将是微小的. 于是,一个复杂系统的物理问题可变成一个简单系统的物理问题加上扰动部分产生的变化量. 例如,要求解微波谐振腔体在放入铁氧体后的谐振频率,在铁氧体体积足够小(可看成微扰)的条件下,就不必直接求解腔体的边值问题[14]. 在本实验中使用TE10p型矩形谐振腔,腔体形状带来的影响可以忽略,以谐振腔整体为研究对象,从谐振腔的微扰理论出发进行理论分析.

设谐振腔内充介质,介电常量为ε,磁导率为μ,则谐振腔内场向量E1、H1满足麦克斯韦方程,即

(5)

(6)

其中,ω0为未加恒定磁场的谐振频率. 若介电常量为ε+Δε,磁导率为μ+Δμ,则谐振腔的谐振频率相应地变为ω=ω0+Δω,这时谐振腔内场向量E2、H2同样满足麦克斯韦方程,即

(7)

(8)

将公式(5)、(6)、(7)、(8)做共轭并相乘,得

(9)

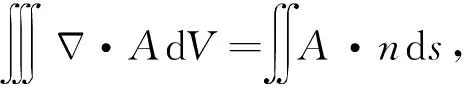
(10)

式(10)是在谐振腔内介质整体改变的情况下导出的,但对腔内部分介质改变时也能适用[15]. 为近似处理微扰情况下介质在小范围内改变的问题,分子的积分范围是铁氧体体积,分母的积分范围是电磁场存在范围体积.

由于样品放在磁场最大、电场为零的位置,因此频率的相对变化量为

(11)

随着恒定磁场H0的增大,铁氧体小球磁导率增大,即Δμ是一个与恒定磁场H0大小有关的量,假设

Δμ=kH0

(12)

则有

(13)

其中,k为待定系数,为正值,r表示样品体积与谐振腔体积之比,是一个小量,则有

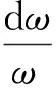
(14)

求解式(14)得

ω=ω0e-vkH0

(15)

显然,谐振腔的谐振频率ω并不是定值,而是随着恒定磁场H0而改变的量ω(H0). 恒定磁场H0增加,谐振腔谐振频率ω减小.

根据文献[16],谐振腔内微波旋转场功率与谐振腔谐振频率ω关系为

(16)

α(>1)为衰减因子,ω′为信号源发出的微波旋转场频率,P(0)为微波旋转场频率ω′与谐振腔谐振频率处于配适状态时谐振腔内微波旋转场功率.

令微波旋转场频率ω′=βω0,并将式(15)代入式(16),得到

(17)

由式(17)可以得到以下结论.

β<1,即微波旋转场频率小于谐振腔谐振频率,谐振腔失谐,谐振腔内微波旋转场功率较小,随着恒定磁场H0的增大,谐振腔谐振频率减小,微波旋转场频率逐渐与谐振腔谐振频率一致,谐振腔内微波旋转场功率变大,因此出现铁磁共振曲线左低右高的现象,如图6(a)、(b)、(c)、(d)所示.

β>1,即微波旋转场频率大于谐振腔谐振频率,谐振腔失谐,随着恒定磁场H0的增大,谐振腔谐振频率减小,微波旋转场频率与谐振腔谐振频率差距进一步增大,谐振腔失谐加剧,谐振腔内微波旋转场功率变小,因此出现左高右低的现象,如图6(e)、(f)、(g)、(h)所示.

5 总结

本实验采用传输式谐振腔测量了铁磁共振曲线,观察到了明显的频散效应,从铁磁体本身对谐振腔谐振频率的影响出发,采用微扰理论,很好地解释了频散效应的产生原因及对铁磁共振曲线的影响,从而解决了铁磁共振实验教学过程中的一个难点.