新课标背景下数学图示作业设计探究

蔡燕清　蔡凤梅

摘要：图示指的是用图形来表示或说明数学概念、方法、过程等。图示作业是教师引导学生利用实物、图形、图表、影像等来诠释数学世界的一种作业，它可使学生降低依赖文字通道的认知负荷，加速思维的发生，利用直观手段把数学思维引向深度和广度。图示作业可以从工具图示、文化图示、分层图示三个角度优化设计，从中实现新课标要求的教学质量评价目标。

关键词：图示作业；新课标；第三学段

《义务教育数学课程标准（2022年版）》（以下通称“新课标”）指出，根据学生的年龄特征，评价结果的呈现应采用定性与定量相结合的方式，关注每一名学生的学习过程。第二、第三学段可以采用描述性评价和等级评价相结合的方式。评价结果的呈现应更多地关注学生的进步，关注学生已有的学业水平与提升空间，为后续的教学提供参考。评价结果的运用应有利于增强学生学习数学的自信心，提高学生学习数学的兴趣，使学生养成良好的学习习惯，促进学生核心素养的发展。基于新课标的要求，在第三学段中，笔者尝试图示作业设计，引导学生将思维过程图示化，既关注学生基础知识和基本技能的获得，又发展学生的数学思维，将学生从繁重的作业中解放出来，回归快乐的学习本源，促进综合素养的提升和自我个性的实现。

一、工具图示作业，让知识从表象走向深入

工具图示作业指的是教师根据考查知识特点，充分挖掘数学工具图（点子图、方格图等）之间的密切联系，进而设计的一种具有延展性的作业。数学学科的发展过程表明，从抽象的数学结论中往往能找到相对直观的表征和解释。很多数学内容和数学概念都既有“数的特征”，又有“形的特征”，为此，教师要明晰一些重要图形工具的用途，如可以用方格图、点子图、笛卡尔坐标图等图形工具，寻找图形之间的联系，让学生不断运用工具图解读问题，探究知识，理解知识的本质意义，使学生对数学知识的认知由表象走向深入。

例如，在教学“求不规则图形的面积”一课时，笔者在多年实践中有这样的经验：学生借助方格纸估计不规则图形的面积，完成作业的正确率较低。在通过割补法和添补法，利用转化的思想把它转化成学过的几个基本图形，然后根据面积和及面积差求出不规则图形的面积时，学生对分割成哪几个已学过的基本图形感到困惑。为此，笔者尝试设计工具图示作业。

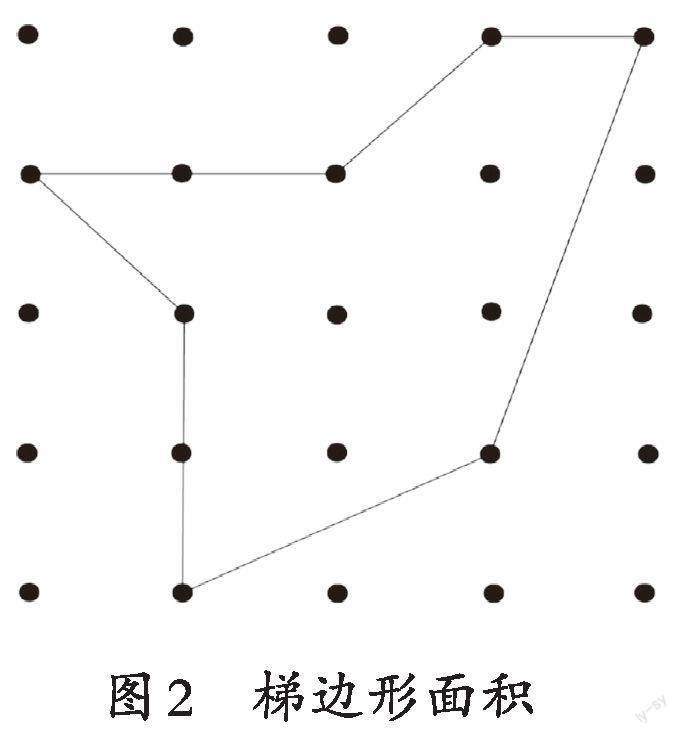
第1题，图1中每个小正方形的边长是1分米，请你算出阴影部分的面积是多少平方分米？第2题，图2中相邻格点围成的最小正方形的面积是1平方厘米，这个多边形的面积是多少平方厘米？第3题，思考：经过图1和图2的面积计算，你能否找到它们之间的联系？利用第2题得到的规律再去解决第1题，感受一下数学抽象的魅力。此处用“割补法”就有一定的困难，图1中因为在割补出基本图形的底长时出现不满一个的边长，部分学生就用添补法，用正方形的面积分别减去4个三角形的面积和2个梯形的面积：4×4-1×3÷2-1×2÷2-1×2÷2-1×2÷2-（3+1）×1÷2-（1+2）×2÷2=6.5（平方分米）。为了继续挖掘图与数的联系，教师可让学生在图2中继续探究其蕴含的数的规律。学生用 “割补法” 很快求出不规则图形的面积是7.5平方厘米后，教师追问：根据你用割补法求出的面积，观察这幅点子图，你能否发现不规则图形的面积跟正方形点阵图中格点的关系？学生通过观察，积极思考，得出：4+9÷2-1=7.5（平方厘米），与刚才的割补法求出的结果是一样的，进而归纳推理得出不规则图形的面积=区域内部的格点数+区域边界上的格点数的一半-1。第3题让学生利用规律去解决图1的问题，学生得到：阴影部分的面积=4+7÷2-1=6.5（平方分米）。学生惊奇地发现，原来求不规则物体的体积能轉化成数格点数。

这样的探究式图示作业设计，需要教师熟悉各种工具图之间的联系，研究它们之间的必然联系，使知识的学习更加全面而富有探究性。

二、文字化图示作业，让知识从空洞走向生动

文字化图示作业，指的是以数学文化名题为载体，让学生展开想象，找到与其匹配的最佳图形来解决问题的趣味性作业。著名数学家柯郎在其论著的《数学是什么》中指出：“数学教育的传统地位陷入严重的危机，数学教学有时竟变成一种空洞的解题训练。”为了让数学走出孤立主义的阴影，教师在设计 数学作业时可以挖掘数学文化名题，结合图示进行设计。这样设计，会让数学作业妙不可言，学生会用图示表征数学文化，通过感性思维与理性思维互换，培养严谨的素质，追求创新精神，欣赏数学之美。

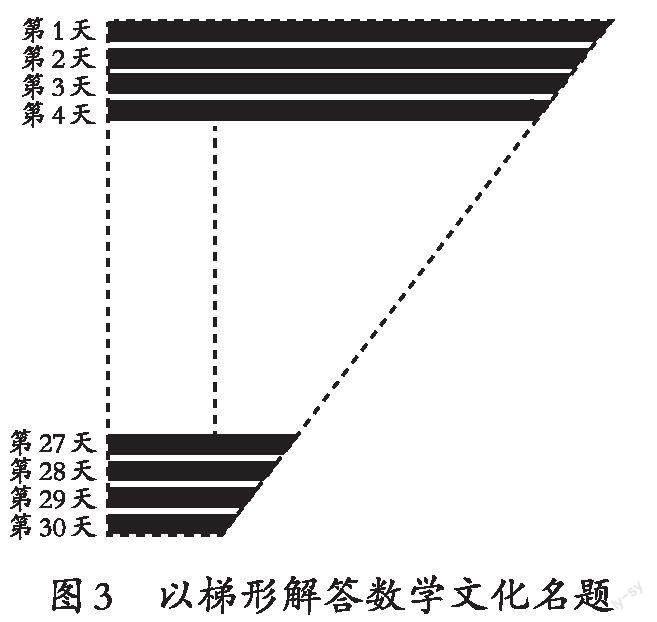
例如，教学“梯形的面积”一课时，教师可设计如下的图示作业：《张丘建算经》是我国南北朝时期数学家张丘建所著，它丰富了我国古典数学理论体系。书中有一道题：“今有女子不善织布，逐日所织的布以同数递减，初日织五尺，末一日织一尺，计织三十日，问共织几何？”意思是：第1日织布5尺，以后每日依次减少， 最后1日织布1尺，一共织了30天，一共织了多少平方尺布？你能利用今天学习的内容，通过画一画，把这道古代数学趣题转化成图形来解答吗？

教师引导学生把纯文字的数学名题转译成几何图形的图示作业，给学生指引思考的方向：画什么图形，怎么画才既能与这道名题的意思相吻合，又能直观解决问题？因为学生刚学完梯形的面积，其思维马上会迁移到梯形上来，他们会尽力想办法把文字名题转译成一个图形题（见图3）。根据梯形的面积公式（上底+下底）×高÷2，学生很快就能算出： （5+1）×30÷2=90（平方尺）。教师可以顺势引导学生继续思考：如何用其他几何图形来解答此题（见图4）？学生先画第一天的一段表示5尺，接着，在后面画第30天一小段表示1尺；如此循环画第二天的4尺和第29天的2尺，就会画出一个长（5+1=6）尺，宽是（30÷2=15）的长方形。最后，根据长方形的面积=长×宽，算出结果也是90平方尺，这也可以为初中等差数列的学习做好铺垫。

新课标背景下，教师可以把图示作业与数学史相结合，展现知识的和谐、方法的巧妙、探究的乐趣、文化的魅力、能力的提升，彰显以德育人的功效。这样，既能使学生巩固梯形的面积应用能力，又能加强数学阅读能力，还能使学生走进经典数学名题，体验古今数学的对话，感悟丰厚的数学文化内涵。伴随着先进的数学文化，数学教学会变得有血有肉。

这样的作业设计要求教师不仅要对数学史作出宏观的历史考查，还要在微观的数学概念、数学方法、数学思想中揭示数学文化底蕴，把数学文化的魅力真正融入作业。这样，数学作业就会更加“平易近人”，就会通过文化层面让学生进一步理解数学，从而喜欢上数学作业，进而热爱数学。

三、分层图示作业，让作业从共性走向个性

经验图示作业要以生活为原型，引导学生用数学的眼光观察生活，从生活中寻找数学灵感启迪来构造数学对象，发现构筑数学作品，从而拓展学生的思维。教师要思考图示作业所蕴含的数学意义和学习价值，贴切地、精准地指向概念本质，揭示概念的内涵，促进每个学生的数学理解。教师要针对不同学生的学习特点，深入分析教材内容，挖掘其背后的价值。为此，教师要思考如何设计分层图示作业，可以结合考查的知识，以多种图示如实物、情境模型、图形等逐级呈现，实施弹性作业设计。

例如，教学“圆柱的表面积”一课之后，为建构圆柱的表面积和圆柱的认识的知识脉络，教师可这样设计分层图示作业。

（一）手切实物，提高兴趣

教师可布置这样的课后作业：拿一根圆柱体的白萝卜切一切，同时将截面涂上颜色，彩印在纸上或将截面覆盖在纸上，描画出截面的平面图形，完成下面表格的填写。

学生在切的过程中可以直观地看到截面的形状，同时也可以直观地发现“切一刀增加两个完全一样的截面”。学生在彩印或描画截面时能清楚地知道“不同的切法，产生的截面不同”，如沿着平行底面切，截面是圆形的；沿着底面直径切，增加的截面是长方形的；不平行于底面而是斜着切，截面是椭圆形的；随意切截面是弓形的……这样的实物操作的图示作业，满足了学生的好奇心，提高了他们做作业的兴趣，使他们在玩中愉快地学习。

（二）手连图形，直观感知

教师可设计如下作业：如下页图5，将不同的圆柱切成两部分，切开后的截面各是什么形状？请连一连。

学生从上一题的实物图，抽象到本题的几何图形，通过想象，进一步深刻认识到圆柱体是通过切割产生图形的，感受到“圆柱体中实物和图形相联系”的道理。同时，通过连线，学生明白了：同一个圆柱被截后的截面形状与所截角度有关，角度不同，截面形状也会随之变化。这样，有利于学生图形的表象积累和空间想象能力的发展。

（三）实际运用，灵活解题

教师可设计如下作业：一根圆柱体木料的底面半径是0.3米，长是2米。如图6所示，将它截成4段，这些木料的表面积比原来木料的表面积增加了多少平方米？

此题的设计目的是利用直观图让学生观察，学生能直接看到多出6个底面。同时，学生根据此图，联想到五年级时所学的“植树问题”的模型，发现截成4段需要截3次，每次多2个底面。根据植树问题模型，学生可以顺势延伸总结规律：如果截成n段，多的截面個数是2（n-1）个。这样，既培养了学生灵活解决实际问题的能力，又兼顾了与其他知识的整合，同时帮助学生建立起模型思想。

（四）课外延伸，发散思维

教师可设计如下作业：明明过生日，妈妈给他买了一个圆柱形蛋糕，蛋糕直径是40厘米，他沿蛋糕直径按十字形纵切（见图7），表面积增加了2400平方厘米 ，爱思考的你能帮明明算出这个蛋糕的高度是多少吗？（请从不同角度思考，用两种方法解答）这样的解题要求激发了学生思考的欲望，学生通过想象得出，第一种解法沿蛋糕直径按十字形纵切，切两刀增加4个面，这4个面是长方形，它的长是底面直径40厘米，宽是圆柱的高，就能轻松得出高是2400÷4÷40=15厘米；学生通过生活经验和观察图形，发现增加8个面，这8个面也是长方形，只不过它的长相当于圆柱的底面半径，宽还是相当于圆柱的高。第二种解法应运而生：2400÷8÷（40÷2）=15厘米。教师渗透这样多种方法的比较，让学生再次感受：不同的思考角度，就有不同的解法。这样，培养了学生解题的灵活性，发散了学生的思维。

学生经过手切、彩印、描画、连线、想象、运用等这一系列层层递进图示作业的训练，多重体验，逐步感悟，建立面与体的联系，在二维和三维之间寻找关系，深化了对圆柱表面积的理解，发展了空间观念。

综上所述，在新课标背景下，图示作业设计应以学生为主体，以尊重学生的个性差异为宗旨，充分挖掘教材资源、生活资源、数学文化、图表资源等的潜在功能，设计有探究性、层次性、思考性、创新性的习题。这样既巩固学生的知识、提高技能，又训练学生的思维，从而激发学生学习数学的兴趣，培养学生的核心素养。

参考文献：

［1］范存丽，让数学思维过程“看得见”［J］.人民教育，2014（15）.

［2］刘焱南，于鹤丹，在高等数学课程中实施数学专题讲座的实践思考［J］.教书育人，2013（12）.