型钢连接装配式混凝土梁等效抗弯刚度研究

2023-10-26胡习兵范周军孙槐璟

计算力学学报 2023年5期

胡习兵, 周莹, 范周军, 孙槐璟

(中南林业科技大学土木工程学院,长沙 410004)

1 引言

装配式建筑由于其低碳节能、工业化制作和施工周期短等典型特征而得到大力推广应用[1]。近年来,针对工程中常用套筒注浆等连接方式存在的弊端,已研发了许多新的装配式PC构件连接方式及做法,其中,采用型钢连接方式的装配式建筑做法尤为突出。装配式PC构件采用型钢连接方式后,构件的抗弯刚度将不同于传统现浇钢筋混凝土构件,必将对构件和结构的刚度与变形带来相应的影响。

国内外学者对变刚度梁以及型钢混凝土梁截面抗弯刚度进行了大量研究,取得了一定的研究成果。朱先奎[2]利用Heaviside函数,将梁抗弯刚度沿轴向的任意变化简化为阶梯刚度,导出了任意变刚度梁变形的计算公式。Lu等[3]给出了弹性模量沿梁轴向及截面高度方向双向梯度变化时功能梯度等截面梁弹性问题的半解析解。许昕等[4]在精确分析梯形梁单元变形特性的基础上,提出了一种新的变截面板簧刚度计算的传递矩阵法。传光红等[5]利用势能驻值原理,得到了变截面梁的单元刚度矩阵及剪切和弯曲位移模式。陈忠汉等[6]在试验研究的基础上提出了不对称钢骨混凝土梁截面抗弯刚度的计算方法。刘凡等[7]基于SRC梁受弯加载试验测得的荷载-挠度曲线,提出了分工作阶段的有效工作截面概念,给出了相应的有效抗弯刚度计算公式。

型钢连接装配式PC构件刚度不同于常规构件,针对该类构件的具体做法,通过计算假定,利用小变形叠加原理,建立了该类变刚度构件的简化计算模型,基于等变形条件,推导了该类构件的等效抗弯刚度计算公式,并对其进行了验证。

2 型钢连接装配式混凝土梁构造

为方便预制混凝土构件的连接,在预制混凝土梁两端设置了型钢连接件,并将梁柱连接节点域采用了组合预制节点,如图1所示。预制混凝土梁两端设置钢结构连接件(丄型钢),丄型钢连接件一端预埋在预制梁内,另一端与预制组合节点的外伸H型钢采用等强对接焊缝进行连接。此类连接采用传统钢结构连接方式,其传力可靠,施工方便,质量可控[8]。

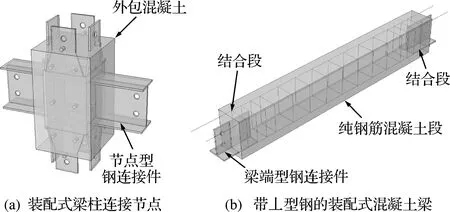
图1 型钢连接装配式混凝土梁构造Fig.1 Construction of fabricated concrete beam connected with section steel

3 构件抗弯刚度计算模型

3.1 计算假设

为简化该类变刚度构件计算,进行如下假设。

(1) 型钢连接混凝土梁截面符合平截面假定; (2) 抗弯刚度为弹性阶段刚度,不考虑连接的非线性性能; (3) 不考虑型钢与混凝土之间的相对滑移。

3.2 计算模型

根据该类梁的构造做法,型钢连接装配式混凝土梁由型钢段、结合段和钢筋混凝土段组成,其中结合段包含丄型钢,型钢段包含H型钢,构件计算模型如图2所示。

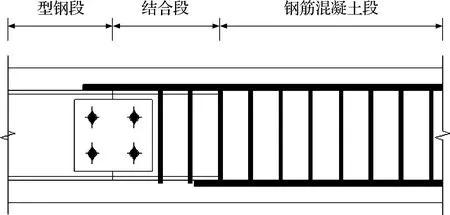
图2 型钢连接装配式混凝土梁计算模型Fig.2 Calculation model of fabricated concrete beam connected with section steel

3.3 抗弯刚度计算方法

根据梁的实际构造做法,梁各段的抗弯刚度可按如下方法进行计算。

(1) 钢筋混凝土段。该段的抗弯刚度B可按照《混凝土结构设计规范》[9]中钢筋混凝土受弯构件的短期刚度计算式求得。

(1)

(2) 型钢段与结合段。型钢段与结合段均为钢-混凝土组合截面,考虑型钢对混凝土约束的影响,其抗弯刚度参考《组合结构设计规范》[10]的规定,当型钢连接装配式混凝土构件的纵向受拉钢筋配筋率为0.3%～1.5%时,按荷载的准永久值计算的短期刚度为

(2)

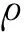
4 等效抗弯刚度计算

4.1 等效抗弯刚度计算方法

采用传统抗弯刚度计算方法进行构件变形计算较为复杂,不利于工程应用。基于等位移原则(即两种方法计算所得挠度相等),由图乘法可得到用等效抗弯刚度代替原有变刚度梁的刚度计算方法。

在荷载作用下,构件位移可计算[11]为

(3)

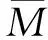
(4)

式中Δ1为钢筋混凝土段在荷载作用下产生的相对位移,Δ2为结合段在荷载作用下产生的相对位移,Δ3为型钢段在荷载作用下产生的相对位移,E1I取值按式(1)计算,E2I和E3I取值按式(2)计算。

主要推导步骤为,(1) 绘制荷载F作用下杆件的弯矩图; (2) 建立虚拟状态,在杆件中施加单位力1,绘制弯矩图; (3) 对以上两个弯矩图进行图乘; (4) 根据等位移原则求出等效抗弯刚度。

4.2 变刚度悬臂梁等效抗弯刚度计算

变刚度悬臂梁在集中荷载F和单位力作用下的弯矩如图3所示,其等效抗弯刚度计算过程如下。

图3 集中荷载下变刚度悬臂梁图乘法计算模型Fig.3 Graph multiplication calculation model of variable stiffness cantilever beam under concentrated load

Δ=Δ1+Δ2+Δ3

(5)

(6)

(7)

(8)

设变刚度悬臂梁的等效抗弯刚度为EI,由材料力学可知等刚度悬臂梁在集中荷载F作用下的梁端挠度为Fl3/(3EI)。由变刚度构件与等刚度构件的挠度相等求解等效刚度,则有

Fl3/(3EI)=Δ1+Δ2+Δ3

(9)

由此可得,变刚度悬臂构件在集中荷载作用下的等效刚度为

EI=E1I/[α3+A/(0.7m)+B/(0.7n)]

(10)

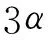
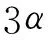
4.3 变刚度简支梁等效抗弯刚度计算

变刚度简支梁在集中荷载F和单位力作用下的弯矩如图4所示,其等效抗弯刚度计算过程如下。

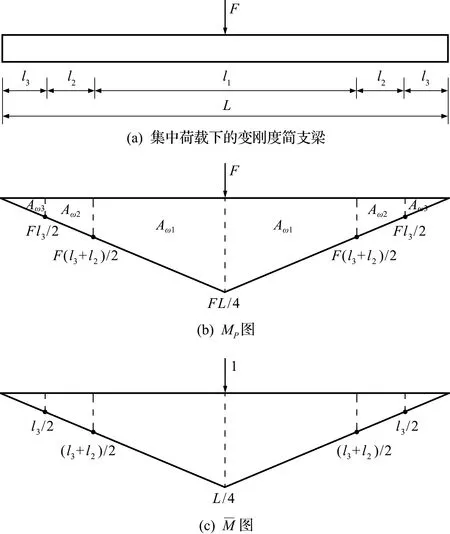
图4 集中荷载下变刚度简支梁图乘法计算模型Fig.4 Diagram multiplication model of simply supported beam with variable stiffness under concentrated load

变刚度简支梁在集中荷载F作用下挠度为

Δ=Δ1+Δ2+Δ3

(11)

(12)

(13)

(14)

设变刚度构件的等效刚度为EI,由材料力学可知等刚度简支梁在集中荷载F作用下的跨中挠度为Fl3/(48EI),由变刚度构件与等刚度构件的挠度相等求解等效刚度,则有

(15)

由此可得,变刚度简支构件在集中荷载作用下的等效刚度为

(16)

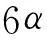
2α(α-β-γ)(α+2β+2γ)

5 对比分析

5.1 试验验证

为验证等效抗弯刚度公式推理的准确性,以变刚度悬臂梁在集中荷载作用下的试验测试数据为例[8]。两试件梁SJL1和SJL2的截面尺寸均为b×h=150 mm×230 mm。试件SJL1钢筋混凝土段的长度为325 mm,试件SJL2钢筋混凝土段的长度为475 mm;试件SJL1与试件SJL2结合段的长度均为175 mm;试件SJL1与试件SJL2型钢段的长度均为250 mm。装配式组合节点、梁、柱和基础均采用C40混凝土,型钢材料为Q355钢,梁端型钢翼缘和腹板厚度均为6 mm,纵筋均采用直径为10 mm的HRB400级钢筋,箍筋均采用直径为6 mm的HPB300级钢筋,外包混凝土厚度为20 mm。

图5 试验Fig.5 Test chart

试验测得极限荷载分别为57 kN和46.5 kN,梁SJL1和SJL2在荷载分别为37 kN和25 kN时,梁端挠度值分别为2.6 mm和3 mm。试件RCL I和RCL II为对称配筋的普通钢筋混凝土梁,通过与型钢连接装配式混凝土梁在相同荷载下的梁端挠度对比分析,研究型钢连接件对梁挠度的影响,列入表1。

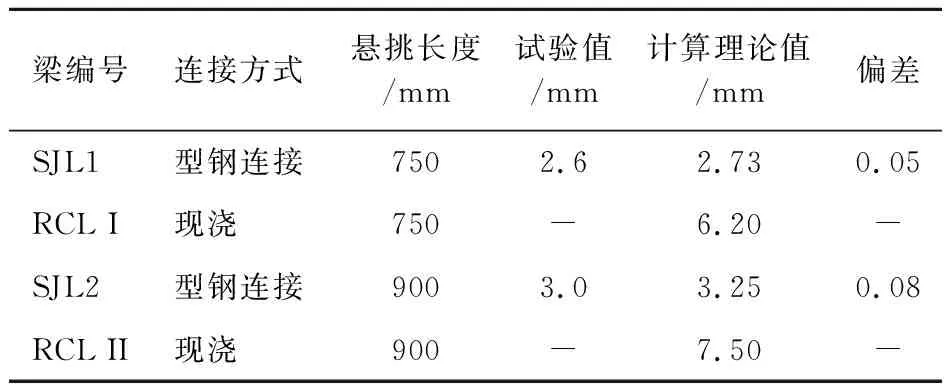
表1 挠度计算理论值与试验值对比Tab.1 Comparison the values between theoretical method and experimental method

5.2 有限元验证

采用有限元软件ABAQUS建立型钢连接装配式混凝土梁试件SJL1和SJL2的有限元模型,混凝土材料本构模型选用损伤塑性模型,钢材本构模型采用双折线随动强化模型,模型采用分离式建模方式,钢筋采用三维桁架线性单元T3D2模拟,混凝土和型钢部件均采用减缩积分实体单元C3D8R模拟,钢筋与型钢焊接通过Merge来模拟,钢筋、型钢与混凝土间采用嵌入约束。混凝土网格尺寸取35 mm,型钢和钢筋网格尺寸取15 mm,如图6所示。

图6 带丄型钢的装配式混凝土梁Fig.6 Fabricated concrete beam with 丄 steel section

有限元分析得到的极限承载力计算值分别为59.6 kN和49.8 kN,梁SJL1和SJL2在荷载分别为37 kN和25 kN时,梁端挠度值分别为2.7 mm和3.06 mm。变刚度悬臂梁挠度计算理论值与有限元理论值对比列入表2。

表2 挠度计算理论值与有限元理论值对比Tab.2 Comparison the values between theoretical method and finite element method

由表1和表2可知,SJL1试件的挠度计算理论值与试验值偏差为5%,挠度计算理论值与有限元理论值偏差为1%,SJL2试件的挠度计算理论值与试验值偏差为8%,挠度计算理论值与有限元理论值偏差为6%,吻合良好。

传统现浇方式的钢筋混凝土试件分别比型钢连接混凝土试件的挠度增大了127%和130%,由此可知,型钢连接混凝土构件比普通钢筋混凝土构件抗弯刚度大,在荷载作用下构件挠度较小,构件和结构受力更为有利。

5.3 参数分析

5.3.1 结合段与型钢段长度对梁抗弯刚度的影响

为研究结合段与型钢段长度对梁挠度的影响,通过改变公式中β和γ的取值,对梁端挠度值进行计算并对比分析。假定梁端荷载为20 kN,梁截面尺寸为b×h=150 mm×230 mm,悬挑长度为1200 mm,型钢腹板和翼缘厚度为6 mm,参数变化及计算结果汇总列入表3。由表3可知,β一定时,随着α减小,γ增大,梁端挠度不断减小,且减小幅度逐渐变缓;γ一定时,随着α减小,β增大,梁端挠度也不断减小,且减小幅度逐渐变缓。此结果表明,在一定范围内,增加型钢连接件的长度能增加梁截面的刚度,减小构件挠度变形值,但随着型钢长度的增加,挠度变形减小的幅度降低,型钢过长得不到充分利用。

表3 变刚度悬臂梁参数变化及计算结果Tab.3 Parameter variation and calculation results of variable stiffness cantilever beam

5.3.2 型钢节点对梁抗弯刚度的影响

为研究型钢节点对梁抗弯刚度的影响,采用有限元软件ABAQUS建立模型RCL1,RCL2与RCL3,试件RCL1为梁截面尺寸300 mm×450 mm,柱截面尺寸450 mm×450 mm,混凝土强度等级C30,型钢强度等级Q355,纵向受力钢筋强度等级HRB400,箍筋强度等级HPB300的标准悬臂梁试件。RCL2为与RCL1同尺寸的对称配筋的普通钢筋混凝土悬臂梁,试件RCL3为与RCL1同尺寸但无型钢节点的型钢混凝土悬臂梁。有限元计算得到RCL1,RCL2与RCL3的荷载-位移曲线如图7所示。可以看出,型钢连接装配式混凝土梁的抗弯刚度最大,其承载力远高于普通钢筋混凝土梁和无型钢节点的型钢混凝土梁,说明型钢节点提高了梁的抗弯刚度;而型钢混凝土梁与钢筋混凝土梁荷载位移曲线相差不大,说明仅含有型钢的钢筋混凝土梁对梁的抗弯刚度影响不大。