考虑碳纳米管非均匀分布的复合材料电导率计算

黄正玮, 宋 颖, 赵晓华*, 侯会明*

(1.汕头大学 土木与环境工程系,汕头 515063; 2.广东省高校结构与风洞重点实验室,汕头 515063)

1 引言

碳纳米管具有优良的力和电性能,近年来在复合材料中作为增强相得到了广泛应用[1-5]。基体材料大多属于不良导体,如聚合物的电导率仅为10-16S/m～10-12S/m[6],而碳纳米管的电导率一般在1 S/m～106S/m[7],因此碳纳米管在改善基体材料的力学性能时,也能大大提高基体材料的导电性能。研究表明,当掺入碳纳米管的体积分数超过某一特征值时,复合材料的电导率会急剧增加到十个数量级以上,之后则缓慢增长,表现出明显的渗流效应[8-13]。这种导电行为主要取决于两种导电机制,即纳米尺度的电子隧穿和微观尺度的导电网络[7,14,15]。同时,研究还发现,碳纳米管复合材料具有压阻效应,即电导率会随所受应变的改变而发生有规律的变化[16,17]。由于具有这一性能,碳纳米管复合材料不仅为结构材料,而且还具有自监测能力,是一种机敏材料。

为了度量压阻效应,准确预测碳纳米管复合材料的电导率尤为重要。迄今为止,已经提出了多种预测复合材料电导率的方法[6,7,18-22]。这些方法主要基于两种途径,一是确定碳纳米管形成的导电网络数量,利用等效电路计算电导率;二是将碳纳米管近似为夹杂,直接用细观力学的方法计算电导率。这些方法不仅考虑了碳纳米管之间的隧穿效应,而且包含了碳纳米管的性能、在基体中的取向和排列方式等因素。这些方法成立的前提都是碳纳米管在基体中均匀分布,而且大多还需要根据试验拟合来确定其中的参数。然而,碳纳米管为团簇材料,分散十分困难,目前还没有制备方法能够实现碳纳米管在基体中的均匀分布,因而限制了这些方法的实际应用。

本文以聚合物基复合材料为对象,考虑碳纳米管在基体中的非均匀分布特性,提出一种计算碳纳米管复合材料电导率的数值方法。采用随机场模拟碳纳米管体积分数,构建了基于细观力学理论的有限元分析模型。只需确定碳纳米管和基体材料的基本物理参数,可有效预测复合材料的等效电导率,从而为碳纳米管复合材料的设计和应用提供依据。

2 碳纳米管非均匀分布的随机场模拟

碳纳米管为团簇材料,在聚合物基体中很难均匀分散,通常呈现不均匀分布的状态,其体积分数在空间上是随机变化的。为了模拟碳纳米管在基体中的非均匀分布,将碳纳米管体积分数视为三维随机场,并采用随机谐和函数来表示。

设碳纳米管的体积分数为f,则可表示为

(1)

(2)

式中N1,N2和N3为随机谐和函数的展开项数。

(3)

(4)

(5)

(6)

(7)

Sfff与自相关函数Rfff之间服从维纳-辛钦关系

e-i(K1ξ1+K2ξ2+K3ξ3)dξ1dξ2dξ3

(8)

从上述各式可知,确定自相关函数后,三维随机场完全可由随机谐和函数表示。文献[23]证明,只需很少的展开项数,式(2)生成的随机场功率谱密度函数就能逼近目标功率谱密度函数,因而具有很高的精度,且近似服从高斯分布。

本文选择高斯型自相关函数

(9)

式中b1,b2和b3为相关距离,反映空间的相关性。代入式(8)可得

(10)

通过误差分析,N1=N2=N3=8时,即可满足精度要求。

为验证模型的可靠性,本文对文献[24]的碳纳米管复合材料进行了数值模拟,尺寸大小取50 mm×50 mm×50 mm。对碳纳米管体积分数为5%的复合材料做了数字化图像研究,得到了反映碳纳米管分散情况的SEM图和等值线图。

图1 碳纳米管体积分数的随机场模拟Fig.1 Stochastic simulation for the volume fraction of carbon nanotubes

图2 碳纳米管体积分数的三维分布Fig.2 Three dimensional distribution of carbon nanotube volume fraction

3 碳纳米管复合材料微小体积单元的电导率

对于任意的微小体积单元,碳纳米管在基体中可近似为均匀分布。复合材料的电导率取决于碳纳米管形成的导电网络和碳纳米管之间的量子隧穿效应。根据Simmons[25]的分析,隧穿效应产生的电导率为

(11)

式中γ为基体的势垒高度,代表电子跃迁穿过基体需要的能量,对于大部分聚合物,势垒高度在0.5 eV～5.0 eV[6,15]。m为电子的质量(m=9.10938291×10-31kg),e为电子携带的电荷大小(e=1.602176565×10-19C),h为普朗克常量(h=6.626068×10-34m2kg/s)。da为碳纳米管之间的平均间距,可由式(12)计算[22,26]

(12)

式中f为碳纳米管的体积分数,dcp和fcp分别为渗流阈值对应的碳纳米管平均间距和体积分数。文献[17]的研究结果表明,dcp=1.8 nm。体积分数fcp可由碳纳米管的长径比α近似求得[18]

fcp=9H(1-H)/(2+15H-9H2)

(13)

基体材料通常为绝缘体,但Simmons[25]的分析表明,由于存在隧穿效应,在碳纳米管之间的基体中会产生隧穿电流。因此,碳纳米管间的隧穿电导率σm即为复合材料基体的电导率。这样,可以利用细观力学的有效介质理论、Mori-Tanaka方法和H-S界限模型[27],进一步求得碳纳米管复合材料微小单元的电导率σe。

(1) 有效介质理论

(14)

式中ne=σe/σm,n=σcnt/σm,σcnt为碳纳米管的电导率。

及S33=1-2S11。

(2) Mori-Tanaka方法

(15)

(3) H-S界限模型

(16a)

(16b)

式中σe+为复合材料电导率的上限,σe-为下限。

4 考虑碳纳米管非均匀分布的复合材料等效电导率

图3 碳纳米管复合材料受电场作用Fig.3 Carbon nanotube composite under electric field

(17)

J=σ·E,·J=0

(18,19)

表面S1

(20)

表面S2

(21)

微分方程(17～19)和边界条件(21)可表示为求下述泛函的极值问题,

(22a)

δπ=0

(22b)

本文采用六面体20结点等参单元进行有限元分析。将计算区域划分为若干个六面体单元,分别取角点及各边中点为结点。对于第e号单元,单元内的电势表示为

(23)

(24)

式(22a)化为

(25)

(26)

式中Ge为转换矩阵,m为结点总数。式(25)变为

(27)

由式(22b)δπ=0,得到线性方程组

(28)

引入边界条件(20),并求解线性方程组(28),即得到所有结点的电势。代入式(23,24)和式(18),可进一步得到各单元内的电势和电流密度J,进而得到表面a和表面b之间的电压U与平均电流I

(29)

(30)

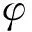
σeq=IL/(US)

(31)

5 方法验证

对图3所示的碳纳米管复合材料进行有限元分析,试件大小为100 mm×100 mm×100 mm。采用20节点正六面体等参数单元,单元边长d=10 mm,共1000个单元。

首先,根据式(1)生成碳纳米管体积分数的随机场,相关距离b1=b2=b3=1d,变异系数cv=0.1,得到各单元的体积分数值。然后,由式(14～16)求得各单元的电导率σe。文献[6,15]的研究表明,聚合物基材料的势垒高度在0.5 eV～5.0 eV,计算中取2.5 eV。碳纳米管的长径比为100,电导率为104S/m[7]。在此基础上,通过上述三维有限元分析,计算出所有结点的电势、各个单元内的电势和电流密度J,利用式(29～31)求得碳纳米管复合材料的等效电导率。

分析中对应每个体积分数值,分别生成50个样本,碳纳米管复合材料的等效电导率取其均值,结果如图4所示。由于碳纳米管的非均匀分布,各个样本的碳纳米管体积分数有着不同的空间分布形式,对应的等效电导率也各异。多个样本的均值是这种非均匀分布的平均反映。本文正是考虑碳纳米管复合材料的随机性,从统计平均的角度计算其电导率。

图4 碳纳米管复合材料的电导率Fig.4 Conductivity of carbon nanotube composites

可以看出,随着掺入碳纳米管的体积分数增加,复合材料的等效电导率快速增大,表现出明显的渗流效应。但超过渗流区后,电导率的增加则逐渐放缓,反映碳纳米管的导电网络基本形成。基于H-S界限理论的有限元分析给出了电导率的上限和下限,尽管不同文献的试验值相差较大,具有随机性,但大部分试验值都在相应的区间内。基于有效介质理论的有限元分析结果偏大,接近H-S界限理论的上限。基于Mori-Tanaka方法的有限元分析结果基本位于H-S上下界的中间位置,反映了试验值的平均变化。因此,考虑碳纳米管的非均匀分布时,基于Mori-Tanaka方法的有限元分析能够给出比较理想的电导率预测值,而基于H-S界限理论的有限元分析则给出了上下界。

6 碳纳米管非均匀分布对复合材料电导率的影响

影响碳纳米管非均匀分布的主要因素为变异系数cv和相关距离,下面基于Mori-Tanaka方法的有限元分析分别进行探讨。分析中,每个碳纳米管体积分数的样本数为100,分别计算其电导率,然后求得复合材料电导率的均值和分布范围。图5(a,b)为变异系数对复合材料电导率的影响。变异系数增加时,碳纳米管的非均匀分布程度加大。可以看出,电导率的离散范围变大,但试验值总是在均值附近波动。cv=0.1时,试验值的波动范围超出了计算的波动范围。而cv=0.3时,试验值基本位于计算范围内。图5(a,c)反映相关距离对复合材料电导率的影响。相关距离反映不同区域碳纳米管分布在空间上的相关性。可以看出,相关距离的改变同样会导致复合材料电导率在一定的范围内波动。

图5 变异系数cv和相关距离对电导率的影响Fig.5 Effect of cv and correlation distance on conductivity

上述结果表明,碳纳米管的非均匀分布对复合材料的电导率有显著影响,本文方法能够对复合材料电导率的均值和变化范围给出合理的预测。

7 结 论

(1) 提出了碳纳米管在基体中非均匀分布的一种模拟方法。通过引入随机谐和函数,建立了碳纳米管体积分数的三维随机场模型。数值结果显示,这一模型能够较好反映碳纳米管的非均匀分布特性。

(2) 基于细观力学的有效介质理论、Mori-Tanaka方法和H-S界限理论,考虑碳纳米管之间的隧穿效应,提出了复合材料微小体积单元的电导率计算方法。在此基础上,建立了考虑碳纳米管非均匀分布的三维有限元分析模型,发展了复合材料等效电导率的计算方法。

(3) 运用上述方法,分析了碳纳米管非均匀分布对复合材料电导率的影响。数值结果表明,碳纳米管体积分数的变异系数和相关距离会导致复合材料电导率在均值附近的一定范围内波动。本文方法能够对均值和变化范围给出合理的预测。