滞回摩擦型调谐惯质阻尼器结构隔震研究
2023-10-26台玉吉华旭刚
台玉吉, 周 帅, 华旭刚*
(1.湖南大学 风工程试验研究中心,长沙 410082;2.湖南大学 桥梁工程安全与韧性全国重点实验室,长沙 410082;3.中国建筑第五工程局有限公司,长沙 410082)
1 引言
结构控制技术可减少结构振动,其主要有主动、半主动或被动控制等,其中被动控制由于不需要外部能量输入和结构形式简单等优点得到广泛研究[1]。惯容器的提出推动了被动控制装置在振动控制领域的进一步发展。惯容器最早是由Smith[2]正式提出的概念,其是一种力与加速度成比例的机械装置,可采用较小的物理质量获得较大的表观质量。这种质量放大的机制,包括滚珠丝杠机制、齿轮齿条机制、液压机制和行星齿轮机制等。
惯容器可单独使用,也可与弹簧和各种耗能元件结合使用,用于结构的振动控制。当单独使用时,惯容器只会增加结构的惯性,从而延长结构的自振周期,降低结构对地震荷载的响应[3]。然而,惯容器本身不会耗散结构的输入能量,因此,其通常与弹簧和能量耗散元件组合使用[4],利用惯容器的局部放大作用提高耗能元件的消能效果[5]。惯容器也可添加到现有的减振器中,以进一步提高减振器的性能,例如调谐液体阻尼器(TLD)和调谐质量阻尼器(TMD)等。TLD使用液体晃动来耗散能量,其原理与TMD类似。为使TLD具备更好的控制效果,必然会增加成本或占用更大的安装空间。文献[6]提出将惯容器和TLD结合形成一个称为调谐液体惯容器系统(TLIS)的控制系统,能够解决成本高和安装空间大的问题。类似的,调谐质量阻尼器惯容器(TMDI)[7]通过惯容器将TMD的质量块与基础相连。TMDI的控制效果和鲁棒性优于传统TMD,MTMDI则更优于TMD[8]。Siami等[9]研究了TMDI的使用,将其用于雕像的地震响应控制。
众所周知,摩擦是用于结构控制最有效的能量耗散机制之一[10]。与粘性和粘弹性阻尼器相比,摩擦阻尼器具有足够的初始刚度、较高的能量耗散能力以及稳定的机械性能,并且显著降低了维护成本。摩擦阻尼器已广泛用于建筑结构的减震和航空航天的发动机振动抑制。与库仑摩擦元件相比,滞回弹簧摩擦元件由弹簧与库仑摩擦元件串联组成,该元件可考虑接触刚度的宏观滑动,因此具有摩擦滞后效应。为了进一步提高调谐惯质阻尼器(TID)在振动控制中的有效性,将滞回弹簧摩擦元件添加到TID中形成一种新型非线性阻尼器——滞回摩擦调谐惯质阻尼器(HFTID)。本文研究HFTID在多层建筑抗震控制中的应用。研究目的是,(1) 进一步降低振动控制系统的力和位移传递率;(2) 建立HFTID最优参数设计公式;(3) 便于HFTID振动控制系统在实际应用中的设计。本文推导了HFTID单自由度系统的运动方程和传递率的解析解,对HFTID进行了优化设计,最后将HFTID应用于基础隔震建筑,验证了HFTID的实用性。
2 HFTID单自由度系统理论推导
图1所示为单自由度力激励系统和位移激励系统,两个系统分别以力和位移作为输入。图1中,fin(t)和fout(t)分别为激振力和传递到基础的力。xin(t)和xout(t)分别为基底的位移激励和主结构的位移响应。力激励系统可用于评估结构在外力(如风、波浪、机械振动和人群振动)下的力传递率,这种力传递率是指传递到基础上的力与激振力的比值。位移激励系统可用于评估受地面运动(如由地震引起的)影响的结构的位移传递率。

图1 HFTID的单自由度系统Fig.1 Single degree of freedom system with HFTID
与线性TID相比,HFTID具有滞回摩擦元件,因此具有滑动摩擦和粘性阻尼的复合阻尼效果。HFTID中的滞回弹簧摩擦元件可在线性和非线性状态之间转换,这取决于主结构和基础之间的相对振幅。临界振幅由摩擦元件的摩擦力和串联弹簧刚度决定。当相对振幅小于临界振幅时,摩擦元件处于静摩擦状态,HFTID可视为TID并联一个弹簧元件。当振幅大于临界振幅时,摩擦元件处于滑动摩擦状态,此时摩擦元件消耗的能量与振幅成比例。HFTID可根据外部荷载调整阻尼器的工作范围,从而将维护和更换成本降到最低。
2.1 非线性摩擦力
本文采用的滞回弹簧摩擦元件由库仑摩擦元件与弹簧串联而成,其力学模型[11-13]如图2所示。其中,kf为串联弹簧的刚度,fn为作用在摩擦阻尼器上的力,f为摩擦阻尼器提供的最大摩擦力。可以看出,摩擦力和位移x1(t)之间的关系可以用分段函数表示为

图2 滞回弹簧摩擦模型Fig.2 Hysteretic spring friction model
(1)
θ=arccos{1-2[f/(kfxA)]}
(2)
位移x1(t)和位移幅度xA之间的关系可表示为
x1(t)=xAcosΨ
(3)
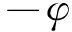
当xA≥f/kf,根据傅立叶变换,非线性摩擦力的表达式可通过式(1,2)得到
fn(Ψ)≅AcosΨ+BsinΨ
(4)
式中
(5)
(6)
当xA fn(Ψ)=kfx1(t)=kfxAcosΨ (7) 对于图1的HFTID单自由度系统,运动方程为 (8a~8d) (9a~9b) (10) 2.2.1 摩擦元件滑动摩擦状态(xA≥f/kf) 摩擦元件处于滑动摩擦状态,摩擦力由式(9)表示。摩擦元件的数学模型是高度非线性的,因此很难直接找到其解析解。谐波平衡法(HBM)是寻找非线性系统近似解的有效方法。在该方法中,假设输入和输出均为谐波,并且使运动方程两侧相同阶次的谐波项的系数相等可得表达式(10)。 简化式(10)可得 (11) 将上述无量纲参数代入式(11)得 (12) 式中 (13) 系统幅值响应可以表示为 FD(λ)=|xg(λ)| (14) 为获得力传递率,式(8a)可进一步表示为 (15) 当结构受到外激励时,其底部的内力可表示为 (16) 传递到基底的力的幅值表示为 (17) 因此,力传递率可表示为 (18) (19) 式中符号‖‖为振幅。 (20) 通过使用无量纲参数,可获得位移传递率 (21) 由式(18,21)可知,力传递率等于位移-位移传递率,这与之前的研究结果一致[14]。 2.2.2 摩擦元件静摩擦状态(xA 摩擦元件处于静摩擦状态,其中摩擦元件可以视为刚性臂。将式(9b)代入式(8)。利用谐波平衡法和无量纲参数,可得 (22) HFTID最优参数可通过以下优化程序确定,优化目标为最小化最大传递率。 (1) 首先,在不同结构阻尼比ζ1条件下对HFTID进行优化设计。将结构阻尼比固定,然后随机组合μ和γk。对每个组合进行计算以确定最佳频率比γω-opt、最优阻尼比ζb-opt和最佳力比γf-opt。 (2) 通过步骤(1),可以得到不同结构阻尼比下最优参数的表达式,再将不同表达式的系数进行拟合,可得到考虑结构阻尼比的最优参数表达式。 考虑拟合精度和拟合公式的复杂性,采用等式(23),基于最小二乘法,获得了不同最优参数的拟合系数。 (23) 最终计算得到位移或力传递率的最优参数的近似公式为 (24) 近似公式的限制条件为0.05≤μ≤0.25,0≤γk≤0.3, 0≤ζ1≤0.03。 为比较HFTID和TID系统的隔振性能,惯质比μ和刚度比γk均设置为0.1或0.2。图3给出了最优参数下TID和HFTID两个系统的传递率比较。HFTID的振动控制系统的最大传递率明显小于TID。HFTID比线性TID更有效,尤其是在共振区和低频区。当惯质比μ为0.1时,γk=0.1和γk=0.2的HFTID的振动控制系统最大传递率比TID小19.5%和17.1%。当惯质比μ为0.2时,与使用TID的隔振系统相比,γk=0.1和γk=0.2的HFTID系统最大传递率分别降低了6.5%和11.8%。应注意的是,在这两种情况下,HFTID系统在高频范围的传递率会增大。本文将传递率的最大值进行最小化作为性能指标,这并不能保证传递率可以在整个频率范围内均具有明显降低效果。 图3 HFTID和TID系统的位移传递率对比Fig.3 Comparison of transmissibility of HFTID and TID systems 为评估HFTID系统在实际工程中的有效性,以1座隔振建筑结构为例对HFTID的隔震性能进行了研究。该结构为五层基础隔震(BI)建筑,分别采用TID和HFTID进行隔震控制,如图4所示。假定结构各层的质量和刚度特性相同,mi=3500 kg,ki=35000 kN/m,其中i={2,3,4,5,6}。基础隔震系统的质量m1和刚度k1分别为3500 kg和105 kN/m,层高为3 m。在OpenSees中建立了简化的有限元模型,如图5所示。 图4 建筑结构Fig.4 Building structure 图5 HFTID基础隔震五层建筑的有限元模型Fig.5 Finite element model of base-isolated five-floor building with HFTID 建筑场地的峰值地面加速度为0.2g,特征周期为0.55 s。根据特征周期,从地震动数据库中随机选择20个地震波,并将峰值加速度调整为0.2g,20个地震波的具体信息列入表1。 表1 随机地震动描述Tab.1 Description of ground motions 由于基础隔震系统的刚度k1远小于结构每层的刚度ki,因此可将基础隔震建筑视为单自由度结构,以获得TID或HFTID的最佳调谐参数。HFTID和TID的惯质比均取0.1,HFTID的刚度比为0.1。基于上述参数,HFTID的最佳调谐参数可根据式(24)获得,γω-opt=0.9483,ζb-opt=0.1936,γf-opt=0.1561,TID的最优参数可根据已有文献[15]计算得到,γω-opt=0.9268,ζb-opt=0.1899。 显然,通过理论计算得到的最优调谐参数都是无量纲参数。在实际应用中,需要确定阻尼器的物理质量、弹簧刚度、阻尼系数和摩擦力。特别是摩擦元件的摩擦力f与外部激励的振幅有关,在地震激励的情况下,外激励是随机的,因此不可能直接获得最佳摩擦力。本文按最不利的情况进行取值,即地震最大响应,将地震加速度峰值和结构总质量相乘得到的惯性力可用作近似优化计算的激励幅值。主结构的总质量为21000 kg,地面加速度峰值为1.96 m/s2,近似的激振力幅值为41160 N,最佳摩擦力为6425 N,具体关键参数列入表2。 表2 HFTID的最佳参数Tab.2 Optimal parameters of HFTID 图6显示了BI系统、BI-TID系统以及BI-HFTID系统在不同地震波下的层间位移角的最大值和均方根值,其中层间位移角定义为层间相对位移与层高之比(Δμ/h)。 图6 建筑物底部层间位移比较Fig.6 Comparison of inter-storey drift at building bottom 图6的水平线是20条地震响应平均值。HFTID的控制性能优于TID。与TID的基础隔震建筑相比,HFTID的基础隔震建筑在20条地震动下的最大地震响应平均值降低了约8.4%。然而,在地面运动Northern Califa-02(第4条地震波)和Lytle Creek(第16条地震波)的情况下,HFTID隔震建筑的最大层间位移角大于TID隔震建筑的最大层间位移角。与最大层间位移相比,层间位移均方根的平均值没有显著降低。这表明HFTID不能同时降低层间位移角的最大值和均方根值。图7显示了隔震建筑在Humbolt Bay和Parkfield地震动作用下的时程响应曲线。显然,HFTID可能会降低最大值,但会放大层间位移角的均方根值。如图7(a)所示,HFTID系统的最大层间位移角显著降低,但在特定时间段(如20 s~60 s)的控制效果可能更差,这导致均方根值降低较差。这主要是由于HFTID的参数优化基于峰值地面加速度,而不是每个局部最大加速度。然而,增加的局部最大值远小于峰值响应,因此上述方法对地震响应控制是合理的。如果期望控制每个局部最大值,则必须采用主动控制或半主动控制。图7(b)中,HFTID可显著降低时程曲线的最大值和局部最大值,这主要是由于强震持续时间短,强震后自由衰减过程长。 图7 建筑物底部层间位移角的时程曲线Fig.7 Time history curves of inter-storey drift at building bottom 图8显示了隔震建筑在20次地震动作用下的TID和HFTID的最大轴向力。HFTID中TID的最大轴向力明显小于单个TID,大部分轴向力由摩擦元件承担,摩擦元件在HFTID中起保护作用。如果TID轴力过大,将导致惯容器中的滚珠(滚珠丝杠机构)或齿轮(齿条齿轮机构)变形,从而减弱减振效果。此外,过大的轴向力也会导致阻尼元件漏油。在HFTID中,摩擦元件承受了大量的力,摩擦元件的内力不会因加速度或速度过大而受损。与TID相比,在HFTID中引入摩擦元件提高了耗能装置本身的鲁棒性。 图8 不同地震波的TID和HFTID轴向力Fig.8 Axial force of TID and HFTID for different seismic waves 本文研究了一种新型非线性阻尼器HFTID。采用谐波平衡方法,研究了具有HFTID的单自由度振动控制系统的力和位移传递率,并推导出了HFTID最优参数的近似表达式,可以根据实际需要调整减振效果,为工程实践中HFTID的参数设计提供一种合适的方法。HFTID在降低结构在多条地震波作用下的最大地震响应方面具有明显的优势,这表明HFTID具有很强的适用性。综上所述,HFTID在建筑和桥梁结构抗震、桥梁拉索振动、车辆悬挂系统和其他机械隔震问题上具有潜在的应用前景。2.2 传递率


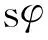
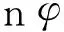
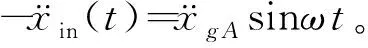

3 HFTID参数优化与隔振性能
3.1 参数优化
3.2 隔振性能对比

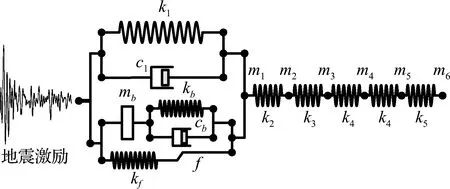
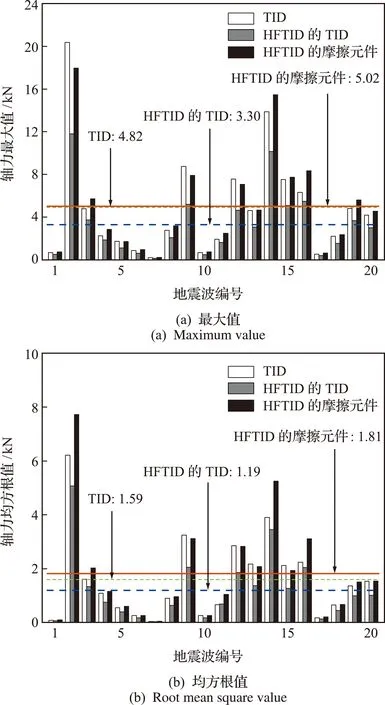
4 隔震性能评估




5 结 论
