基于分离式建模的砖石古塔动力性能与响应分析

2023-10-26卢俊龙周谦祥田鹏刚王振山田建勃

计算力学学报 2023年5期

卢俊龙, 周谦祥, 田鹏刚, 王振山, 田建勃

(1.西安理工大学,西安 710048; 2.陕西省建筑科学研究院有限公司,西安 710082)

1 引言

我国现存的砖石古塔建造年代久远,长期受到自然和人为的破坏,其结构均出现损伤,同时塔体高宽比大,砌体粘结强度较低,在地震作用下极易发生破坏。对古塔进行地震反应分析,针对其地震响应与破坏的动力学机制,进行科学合理的抗震能力评定与性能提升,是砖石古塔预防性保护的必要工作。作为由古旧砌体构成的高耸结构,古塔在地震作用下与地基的动力相互作用十分明显,同时古塔砌体在动力作用下的开裂破坏对塔体动力响应具有显著影响,因而需要考虑上述因素的影响,对砖石古塔动力性能与地震响应进行精细化分析,为其抗震性能评估与加固修复提供依据。

砖石古塔抗震加固分析的研究中,国内外学者通过对其现状和震害特征进行调查,归纳分析砖石古塔的破坏模式,围绕倒塌机制、地震易损性和地震响应等课题开展了一系列研究工作[1-3],对部分古塔通过环境激振试验测得其动力特性,与数值仿真结果进行对比,研究古塔的地震响应规律[4,5],分析开洞位置、壁厚和相邻建筑物对其抗震性能的影响[6,7],提出评估砖石古塔结构地震易损性的参数[8],结合典型古塔的地震作用分析研究,探讨古塔计算模型的建立方法[9],通过建立砖石古塔有限元模型,对古塔进行增量动力弹塑性分析和push-over分析等,评估古塔抗震性能[10],提出部分砖石古塔抗震加固方案[11],取得了较好的成果。

上述研究大多通过简化计算模型,并未考虑地基对结构动力性能的影响,直接将结构与地基嵌固,对古塔结构进行数值仿真分析,通过计算结构的动力特性、动力响应、进行push-over分析、将模拟结果与环境激振试验结果进行对比等,分析砖石古塔结构的抗震性能。

针对土-结构相互作用对砖石古塔动力性能与响应的影响已有诸多的研究,但数值分析多采用整体式建模,而古塔由砌块与砌筑灰浆构成,因此块体与砌筑灰浆的破坏机制很难获得理想结果。Casolo等[12]研究了地基土体积与不同地基土类型对古塔动力响应和地震破坏模式的影响。Bayraktar等[13]研究了三种不同地基土对砖石拱桥-土相互作用系统的三维地震破坏机理影响。Silva[14]评估了土-结构相互作用对砖石塔的周期、阻尼、位移和塔体整体动力响应的影响。Fathi等[15]采用数值分析法,提出土-结构相互作用会对古砌体结构平面外性能产生影响。Torelli等[16]提出三种不同评估等级,对某塔楼和地基相互作用系统的抗震能力进行了评估。

研究表明,与刚性地基条件下古塔结构相比,古塔与地基相互作用体系的自振频率低,阻尼增大,地震时能量以塔体结构开裂变形与土体中的辐射阻尼而耗散。同时历史震害表明,沿砌筑灰缝破裂是古塔结构震害的主要形式,因而本文通过考虑土-结构相互作用以及古塔砌体中块体与灰缝的分布关系,进行砖石古塔动力特性与地震响应研究,为砖石古塔的抗震保护提供参考。

2 古塔数值计算模型

2.1 慧照寺塔概况

慧照寺塔位于陕西省渭南市临渭区,唐代砖塔,如图1所示,2013年入选全国重点文物保护单位,为楼阁式砖塔,平面为正方形,共9层,总高36 m,首层平面边长约6.11 m,层高为5.75 m,2层以上层高和宽度逐层递减,首层北面开设门洞,有塔室且内部有楼梯,其余各层四面均有假券门,层间有砖砌叠涩出檐,结构尺寸列入表1。

图1 慧照寺塔Fig.1 Huizhaosi pagoda

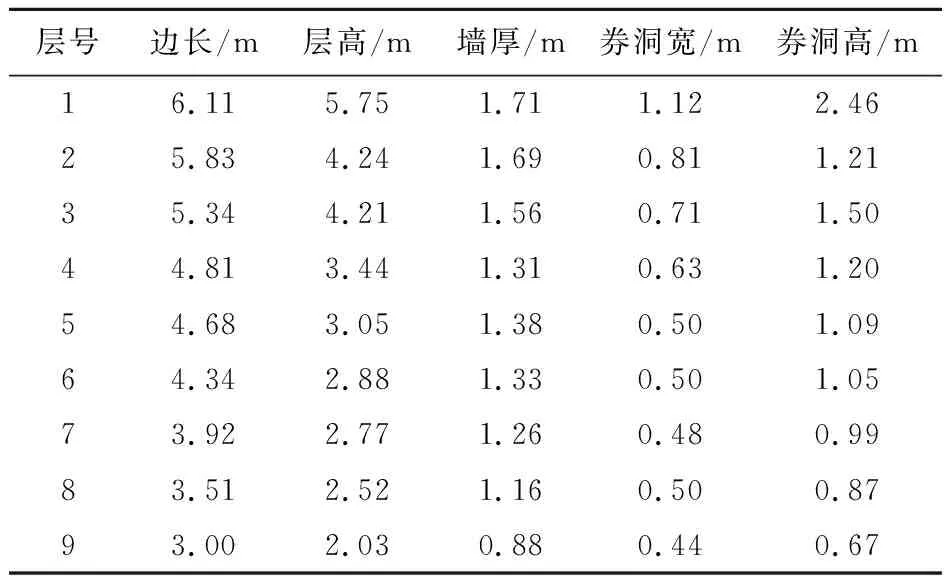
表1 慧照寺塔楼层尺寸Tab.1 Dimensions of the Huizhaosi pagoda

2.2 地震波输入

古塔所处场地抗震设防烈度为8度,设计地震分组为第二组,因其为全国重点文物保护单位,分析时提高1度按9度设防计算。因无场地地质资料,结合渭南地区场地条件取为III类,根据其场地类别,特征周期值为0.45 s,及古塔自振周期为0.79 s,选择El-Centro地震波、Taft波及兰州人工波作为地震动输入,具体波形和频谱曲线如图2所示,按小震、中震和大震的设防水准对加速度进行调幅后分别输入到塔底和地基底部。

图2 三条地震波加速度时程曲线和频谱曲线Fig.2 Three acceleration time history curves of seismic wave and spectrum curve

2.3 计算模型

2.3.1 塔体结构

基于通用有限元软件ABAQUS平台,考虑古塔砌体的构造特征,将砖材块体与灰浆分别按一定的等效尺寸分离后赋予相应的材料属性参数,建立慧照寺塔的数值计算模型,如图3所示。计算单元采用8结点六面体单元,塔体青砖弹性模量E=1000 MPa,泊松比μ=0.15,密度ρ=1800 kg/m3。

图3 塔体结构数值模型Fig.3 Finite element model of the structure

阻尼比依据设防水准进行取值,小震取2%,中震取3%,大震取4%。糯米灰浆的弹性模量E=100 MPa,泊松比取μ=0.15,依据砌体试块及灰浆试块的抗压试验,确定塔体损伤模型的力学参数,砌体的轴心受压峰值应力fcm=4 MPa,峰值应变εcm=0.04 MPa,轴心抗拉强度平均值ft=0.02 MPa,峰值拉应变εt=0.02 MPa,分别定义青砖和灰浆的损伤参数[17]。受压与受拉损伤的参数为

(1)

受拉损伤参数

(2)

式中Dc和Dt分别为受压和受拉损伤因子,ε为压应变,ε为极限压应变,ε为极限拉应变。

2.3.2 地基边界条件

第一层土Ed1=22700 kPa,σdf1=134 kPa

第二层土Ed2=35700 kPa,σdf2=139 kPa

第三层土Ed3=45000 kPa,σdf3=146 kPa

地基的边界采用粘弹性人工边界,在ABAQUS相互作用模块中特殊设置法向和切向弹簧阻尼器,边界节点各方向均设置1个单向弹簧-阻尼单元,形成连续分布的并联弹簧-阻尼器系统,如图4所示。弹簧的法向刚度、法向阻尼、切向刚度和切向阻尼参数按下式计算[19]

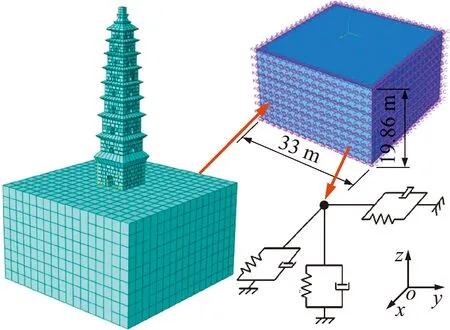
图4 塔体-地基相互作用系统计算模型Fig.4 Calculation model of tower-foundation interaction system

切向边界KBT=αTG/R,CBT=ρcs

(3)

法向边界KBN=αNG/R,CBN=ρcp

(4)

考虑地基条件后,建立塔体-地基相互作用系统的计算模型如图4所示,计算时每个粘弹性边界节点的从属面积为4 m2,地基计算模型四个面共包含680个人工边界节点。

3 动力特性

通过模态分析计算得到慧照寺塔的前2阶平动振型如图5所示,底部刚接时,东西向1阶和2阶振型质量参与系数分别为48.6%和27.1%。考虑土-结构相互作用后,东西向1阶和2阶振型质量参与系数变为79.7%和7.9%。由表2可知,考虑土结构相互作用后,对1阶振型影响不大,其自振频率降低5.7%,周期略有增加;2阶振型影响较大,自振频率降低了45%,自振周期增加显著。

图5 振型Fig.5 Vibration mode

表2 自振频率计算结果比较Tab.2 Contrast of vibration frequencies

4 地震反应

4.1 水平地震响应

4.1.1 加速度

计算得到El-Centro波在三种设防水准下两种模型沿水平东西方向的加速度放大系数,如图6所示。当塔底嵌固时,加速度放大系数曲线随楼层高度总体呈S形分布,在9层顶部其值最大,且不同工况下其值的大小关系为中震<大震<小震。

考虑地基-结构相互作用时,小震和中震作用下,加速度放大系数曲线随楼层高度总体呈C形分布,曲线拐点分别出现在4层和6层,为曲线的最小值。大震作用时,在第2层至第7层出现多个连续拐点。

对比图6可以看出,与底部刚接相比,考虑地基-结构相互作用后,曲线拐点发生改变,塔体1层的加速度放大系数值较底部嵌固条件时显著增大,其原因为土体的放大效应。

表3为东西向峰值加速度具体数值,可以看出,大震时,考虑土-结构相互作用时各楼层水平向峰值加速度放大系数均大于底部嵌固时的值。

表3 东西向峰值加速度放大系数Tab.1 Amplification factor of East-West peak acceleration

图7～图9分别为El-Centro波、Taft波及兰州人工波作用下塔体顶层的加速度时程曲线,表4为顶层加速度峰值,模型A为底端嵌固条件下,模型B为考虑土-结构相互作用条件下,其中在El-Centro波和Taft波作用下,考虑土-结构相互作用后,古塔结构的东西向和南北向的水平加速度峰值均大于底部嵌固时的值。而当输入兰州人工波时,考虑相互作用条件下古塔加速度峰值响应均较底部嵌固条件下的值减小约50%,其原因在于输入的兰州波主频与系统的主频相差较大,土层对地震波起到隔振作用[21]。

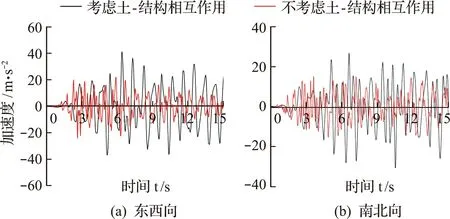
图7 El-Centro波作用下顶层加速度时程曲线Fig.8 Time history curve of top floor acceleration under EI wave

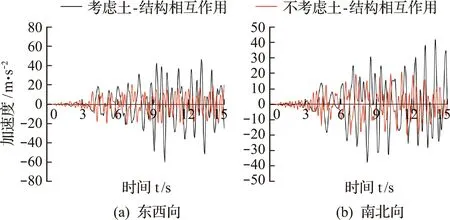
图8 Taft波作用下顶层加速度时程曲线Fig.9 Time history curve of top floor acceleration under Taft wave

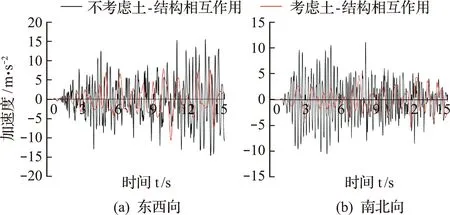
图9 兰州人工波作用下顶层加速度时程曲线Fig.9 Time history curve of top floor acceleration under Lanzhou wave

表4 顶层加速度峰值Tab.4 Top acceleration peak

4.1.2 位移

图10为El-Centro波作用下塔体顶层水平位移响应,从图11(a)时程曲线可以看出,考虑土-结构相互作用后,东西向峰值水平位移由2.41 cm增加到6.93 cm。从图10(b)层间位移曲线可以看出,考虑土-结构相互作用后,曲线拐点发生改变,东西向最大层间位移由七层变为首层,其值由3.39 cm增加到13.39 cm。

图10 水平位移响应Fig.10 Horizontal displacement response

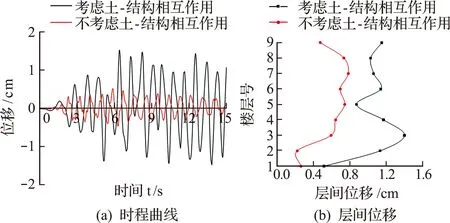
图11 竖向位移响应Fig.11 Vertical displacement response

4.2 竖向位移

图11为El-Centro波作用下塔体顶层的竖向位移响应,从图11(a)时程曲线可以看出,考虑地基-结构相互作用后,塔体竖向峰值位移响应约为底部嵌固条件下其值的3倍。从图11(b)层间位移曲线可以看出,底部嵌固时,竖直向层间位移最大值位于7层,其值为0.78 cm,最小值位于2层,其值为0.22 cm;而在考虑相互作用条件下,楼层的竖向层间位移均大于底部嵌固时的值,最大位移值为1.4 cm,位于第3层。

4.3 应力

4.3.1 主拉应力

因古塔砌体抗拉强度低,地震作用下易发生受拉破坏,塔体在所输地震波峰值时刻的最大主拉应力计算结果如图12～图14所示。表5为主拉应力峰值,模型A为底端嵌固条件下,模型B为考虑相互作用条件下。可以看出,不同设防水准下3条波作用下塔体最大主拉应力峰值及其出现的位置均不相同,塔体主拉应力峰值关系为,Taft波作用下最大,兰州人工波作用下最小;同一设防水准下相同地震波作用时,两种模型的主拉应力响应不同。如在El-Centro波作用下,当塔底部嵌固时,小震、中震和大震作用下塔体最大主拉应力分别位于2层西立面洞口周边、4层南立面洞口处和4层东北立面交界处,其值分别为0.367 MPa,0.414 MPa和1.359 MPa。当考虑地基-结构相互作用条件,El-Centro波作用时,小震、中震和大震作用下塔体最大主拉应力分别位于4层东北立面交界处、4层东北立面交界处及东立面洞口处和4层东北立面交界处,其值分别为0.416 MPa,2.833 MPa和4.124 MPa。与塔底部嵌固相比,考虑地基-结构相互作用后,塔体最大主拉应力峰值及位置发生变化。

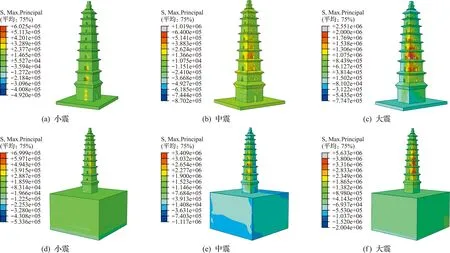
图12 El-Centro地震波下最大主拉应力云图Fig.12 Cloud chart of maximum principal tensile stress under EI-Centro seismic wave

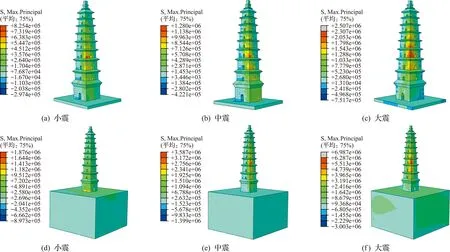
图13 Taft地震波下最大主拉应力云图Fig.13 Nephogram of maximum principal tensile stress under Taft seismic wave

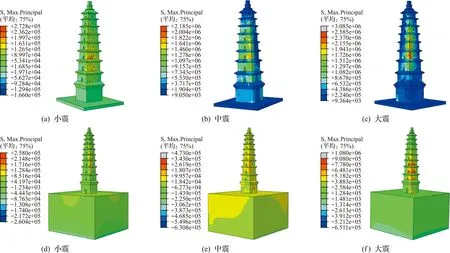
图14 兰州人工地震波下最大主拉应力云图Fig.14 Cloud chart of maximum principal tensile stress under artificial Lanzhou seismic wave

4.4 等效塑性应变

依据等效塑性应变云图分布进一步判断塔体的开裂变形特征,3条地震波下慧照寺塔等效塑性应变如图15～图17。可以看出,不同地震烈度下三条波作用下塔体最大等效塑性应变位置不同。

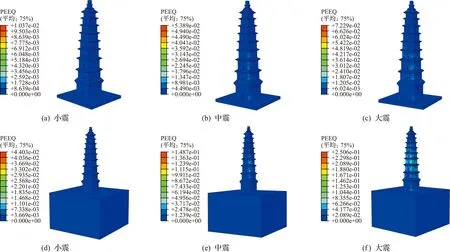
图15 El-Centro地震波下等效塑性应变Fig.15 Equivalent plastic strain diagram under El-Centro seismic wave

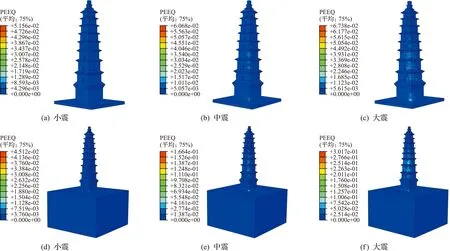
图16 Taft地震波下等效塑性应变Fig.16 Equivalent plastic strain diagram under Taft seismic wave

图17 兰州人工地震波下等效塑性应变Fig.17 Equivalent plastic strain diagram under artificial Lanzhou earthquake wave

如小震时,三条波作用下,两种模型塔体均产生明显开裂变形。中震时,在底部嵌固条件下,El-Centro波、Taft波和兰州人工波塔体等效塑性应变最大值分别位于2层至4层东南立面交界区、塔体3层至4层东北立面交界区和1层洞口顶部及各层南立面洞口附近灰缝处。在考虑地基-结构相互作用条件下,El-Centro波、Taft波和兰州人工波塔体等效塑性应变最大值分别位于2层至4层东南立面、1层底部及2层至5层东北立面交界区和1层底部。

与底部嵌固条件下相比,考虑地基-结构相互作用后,小震时塔体塑性应变均未发生明显改变;中震作用时,El-Centro波作用下,塔体在2层至4层东南立面交界区等效塑性值增大;Taft波作用下,塔体最大等效塑性应变区由3层至4层东北立面交界区扩展到2层至5层东北立面交界区。兰州人工波作用下,塔体在1层底部等效塑性应变值最大。大震作用时,El-Centro波作用下,塔体最大等效塑性应变区域由2层至4层东北立面交界区扩展到2层至5层整个楼层,同时等效塑性应变值增加;Taft波作用下,塔体等效塑性应变区由2层至4层东北立面交界区向全截面扩展。兰州人工波作用下,塔体在1层底部及3层至4层东南立面交界区等效塑性应变值较大。

5 慧照寺塔结构地震响应分析

采用分离式建模后,通过赋予不同材料属性参数,进行地震作用下塔体在不同设防水准下的开裂破坏过程模拟计算结果表明,慧照寺塔在地震作用下,结构薄弱层位于2-5层。El-Centro波作用下,底部嵌固时,南北向层间位移曲线拐点出现在2层和5层,考虑相互作用后,沿南北方向的层间位移曲线拐点出现在3层、5层和8层,结构薄弱层发生变化。同时,与底部嵌固相比,考虑相互作用后,El-Centro波和Taft波作用下塔体顶部加速度峰值响应增加,而兰州人工波作用下加速度峰值响应反而减少50%,可以看出,考虑地基-结构相互作用后,塔体薄弱层及动力响应的分析结果均发生变化。

同时,由塔体等效塑性应变云图分布可以看出,因砌筑灰浆的粘结强度远低于砌块强度,地震时灰缝首先发生开裂变形,随输入地震烈度的提高,砌块逐渐发生开裂,而在考虑地基与结构相互作用条件下,土体对地震波具有一定的放大作用,塔体的变形开裂加剧。