近极槽配合下直驱电机性能分析

兰志勇,叶书帆,谭皓元,罗元钧,彭思齐,2

(1.湘潭大学 自动化与电子信息学院,湘潭 411105; 2.佛山湘潭大学绿色智造研究院,佛山 528300)

0 引 言

直驱电机(以下简称DDM)具有高效率、高转矩密度的特点,其凭借着高定位精度、快响应速度及大转矩的优势,不需要齿轮、皮带等减速装置而直接连接在工作台上,因此被广泛应用于多功能高性能数控机床、高精密检测装置、印刷机械制造等自动化生产设备中。而如何在现有DDM的基础上进一步提升电机的定位精度及减小转矩脉动成为了当今科研工作者追求的目标。齿槽转矩的存在会对电机的定位精度产生较大的影响,怎样有效地抑制或消除齿槽转矩对DDM的影响成为近年来研究的热点问题。不同的极槽配合会对DDM的齿槽转矩产生较大的影响,同时合理的极槽配合选择也能优化气隙磁密与反电动势波形,从而提升电机的性能。

目前,许多专家学者主要通过电机本体结构设计对DDM进行优化设计,优化方向主要集中在合理的极槽配合、斜极[1]、斜槽、不等齿宽[2]、辅助槽[3]、极弧系数、转子偏心[4]、不等气隙等方面。其中,文献[5]对不同极槽配合下无刷直流电机的分数槽集中绕组的绕组系数进行了研究,提出了虚拟电机的概念来计算分数槽集中绕组系数,并提出一系列性能较好的极槽配合。文献[6]研究了不同极槽配合交替极永磁电机的齿槽转矩与不对称气隙磁密中偶次谐波的关系,并探究了极槽配合对交替极永磁电机反电动势偶次谐波与转矩脉动的影响。文献[7]针对六种极槽配合方案结合遗传算法对电机的永磁体厚度、槽深、齿宽等进行优化,选择出一组低齿槽转矩、高功率密度、低损耗的电机。文献[8]对多相直驱电机的转矩脉动和损耗特性进行了研究,分析了三相电机与十五相电机的谐波含量与损耗,得出十五相电机在不同供电方式、不同中性点接法和不同极槽配合下的转矩脉动和损耗方面具有显著优势。文献[9]结合绕组系数解析式对比分析了不同极槽配合下的各次谐波绕组系数及幅值,选择出一组合适的极槽配合组合,对比分析不同负载状态下的电磁转矩及其他电机性能,得到不同极槽配合方式对电机设计及其性能的影响。文献[10]使用多层绕组排列合成具有非常规极槽配合的对称分数槽集中绕组,并提出了一种通用的设计方案,结合常规极槽配合分析非常规极槽配合的分数槽集中绕组电机的优缺点,进行了样机测试,验证了该想法的可行性。文献[11]通过对分数槽集中绕组的电枢绕组磁动势谐波及电枢反应磁场谐波分析,从绕组分布效应、相移技术、内置磁障及定子齿槽结构4个方面总结了分数槽集中绕组电机减少谐波的方法,同时对发展趋势进行总结与展望。文献[12]引入虚拟电机的概念并结合星型图分析了分数槽虚拟电机与整数槽虚拟电机绕组计算的等效条件,对分数槽集中绕组的绕组系数快速计算提供了方法。

本文在上述文献的基础上,针对应用于数控机床的DDM极槽配合选择进行分析,结合电机的齿槽转矩、转矩脉动、气隙磁密与反电动势波形畸变率对DDM的性能进行综合性评估,选择出性能参数较优的极槽配合。在结构参数相同的前提下,将待选的几种不同极槽配合的电机模型通过有限元分析进行对比,为DDM在数控机床上的应用提供了重要的参考依据。

1 DDM齿槽转矩的研究

1.1 齿槽转矩的理论分析

齿槽转矩用能量法可表示为永磁电机不通电时磁场能量W与定转子相对位置角α的负导数[13],即:

(1)

假设电枢铁心的导磁率为无穷大,永磁材料的磁导率为真空磁导率。

规定α为定转子相对位置角,θ=0为该永磁体的中心线,如图1所示。

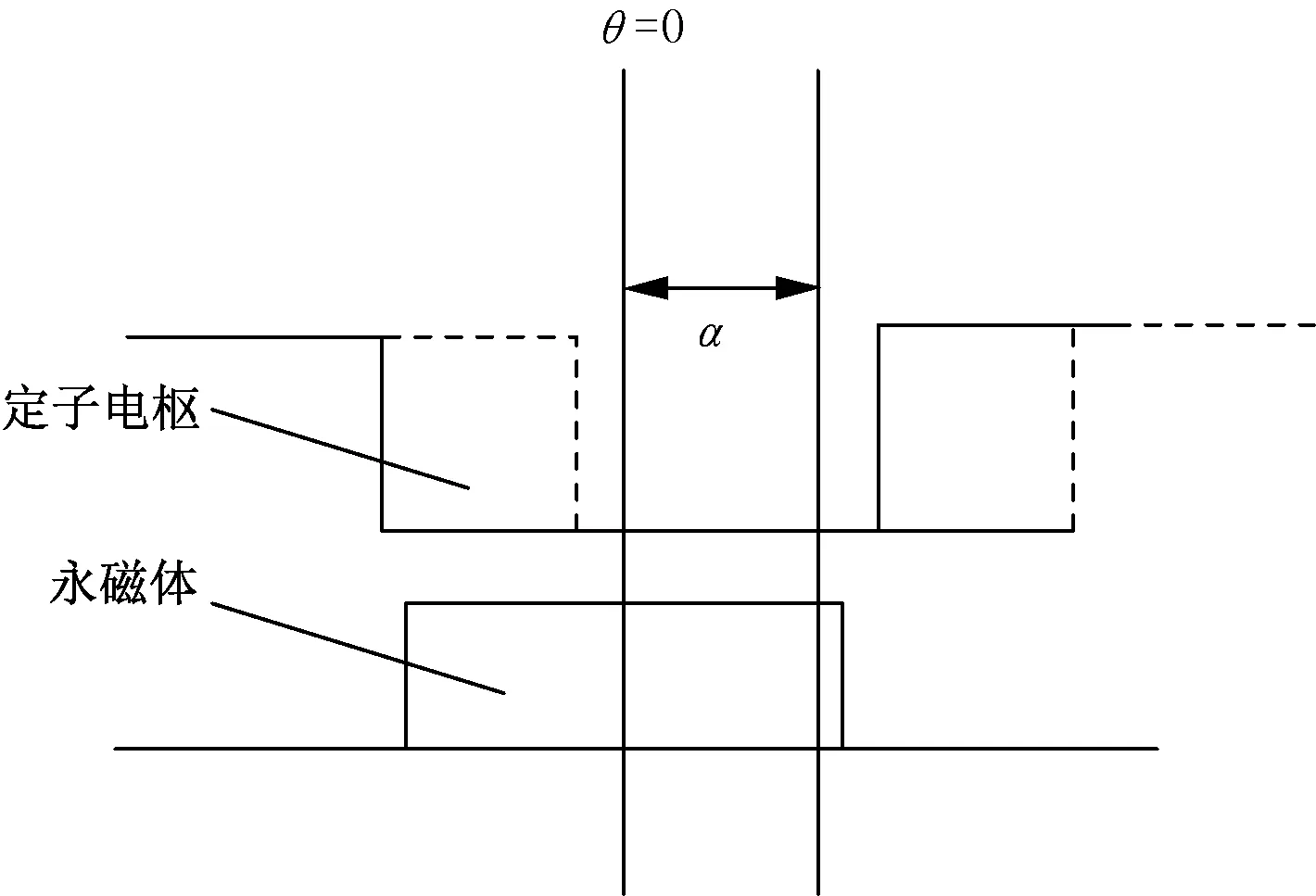
图1 定转子相对位置角

假设电机内储存的能量可近似为电机永磁体中储存的能量和电机气隙中所储存的能量之和,即:

(2)

气隙磁密在定子电枢表面的分布可表示:

(3)

式中:Br(θ),δ(θ,α),hm(θ)分别为永磁体剩磁、有效气隙长度、永磁体磁化长度沿圆周方向的分布。

将式(3)代入式(2)可得:

(4)

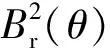
(5)

将上述公式整理后可得出:

(6)

式中:Lef为电机电枢铁心的叠压厚度;R2、R1分别为转子外径、定子轭内径;n为能使nQ/(2p)为整数的整数。

1.2 极槽配合对齿槽转矩的影响

本文针对某数控机床上转台用DDM的极槽配合进行分析,在已经确定槽数的情况下,通过改变极数来影响极槽配合的选择,进而影响Gn和Brn的大小来抑制齿槽转矩。在电机槽数为27的情况下,本文选择极数与槽数相近的槽极配合组合,极数分别为24、26、28、30。

DDM的定转子位置在一个齿距范围内发生相对变化的过程中,齿槽转矩也相应呈周期性变化,其周期数Np由槽数与极数的组合决定,周期数为使nQ/(2p)为整数的最小整数n,故在一个齿距内的齿槽转矩周期数的表达式:

(7)

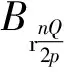
结合表1中的4种极槽配合DDM齿槽转矩的周期数可以发现,极槽配合为27/28的DDM齿槽转矩周期数最大,27/26、27/30与27/24次之。根据上述理论可以预测到极槽配合为27/28时DDM的齿槽转矩最小,极槽配合27/26的齿槽转矩次之。

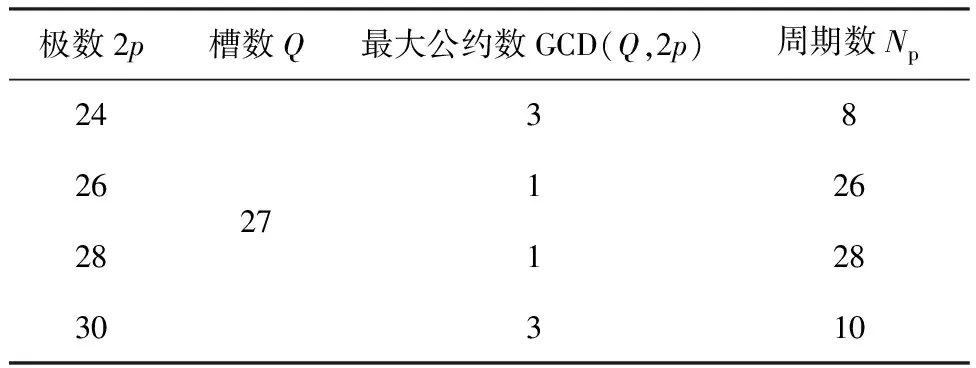
表1 4种极槽配合的最大公约数与周期数

2 气隙磁场谐波含量分析

电机气隙是进行能量交换的场所,气隙内进行能量交换是电机运行的基本原理,气隙磁场对电机的影响主要表现在:影响齿槽转矩的大小;气隙磁场谐波的存在会导致电机产生较大的噪声;造成较大的铁心损耗,使电机温度上升等。此外,电机在进行能量交换的过程中,气隙磁场中存在的各次磁场谐波会对电机性能产生较大的影响,因此对气隙磁场进行分析很有必要。

合理的极槽配合来削弱气隙磁场谐波含量可以达到改善反电动势和气隙磁密波形及提升材料利用率的目的,而电机的绕组系数会对这些参数产生影响,因此在对反电动势与气隙磁密分析的过程中,分析其绕组系数非常有必要。

近极槽配合下的绕组系数由节距系数与分布系数组成,其中节距系数表达式:

电机的分布系数可表示:

式中:kp,kpv分别为基波分布系数和v次谐波谐波分布系数;q,α,v分别为每槽每极相数、槽距角和v次谐波的次数。

近极槽配合下DDM的绕组系数可表示:

式中:kw,kwv分别为基波绕组系数和v次谐波绕组系数。

本文选择的27/24、27/26、27/28和27/30 4种极槽配合下的绕组系数,其基波绕组系数如表2所示,图2为各极槽配合下的基波及各奇数次谐波绕组系数。

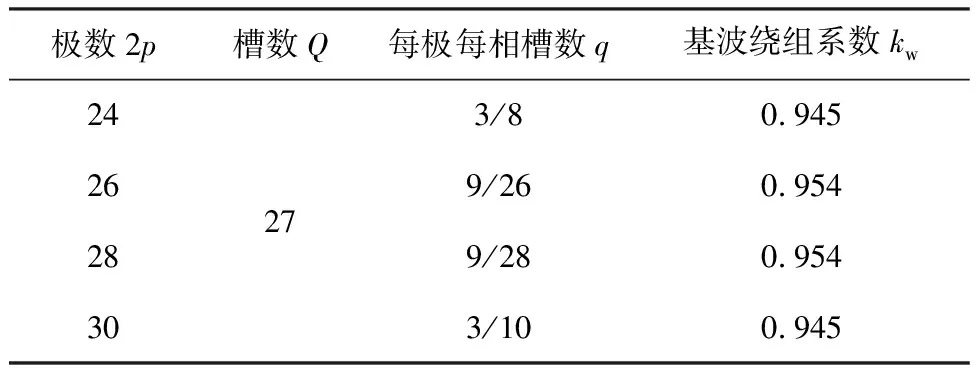
表2 不同极槽配合下的基波绕组系数

图2 不同极槽配合下的各奇数次谐波绕组系数

由图2与表2可以发现,极槽配合为27/24与27/30的DDM绕组系数相同,27/26与27/28亦是如此,故对上述4种极槽配合下的DDM绕组系数分析可以简化为对27/28与27/30的分析。由图2与表2数据可知,极槽配合为27/28的基波幅值比极槽配合27/30的大,同时极槽配合27/28的3～11次奇数次谐波均比极槽配合27/30的幅值较大,但极槽配合27/28的13～19次奇数次谐波的幅值明显比极槽配合27/30的幅值较小。极槽配合为27/28的各奇数次谐波值随谐波次数的增加而减小,这表明极槽配合为27/28的DDM绕组系数分布相对较好。由于分数槽绕组的电机具有分数次谐波,所以要结合仿真结果进一步分析电机的性能。

3 近极槽配合下DDM性能分析

3.1 仿真模型搭建

为探究4种极槽配合下的DDM性能,在保证电机的结构参数和输入变量保持一致的前提下,对这四种电机通过Soildworks进行精确建模,将模型导入到Maxwell中,对模型进行材料添加并给定相同的输入参数,对仿真模型进行有限元分析得到结果。四种极槽配合下的DDM结构参数如表3所示。

表3 四种极槽配合DDM的结构参数

结合上述参数,将精确建模导入到Maxwell中进行材料添加、运动设置添加、激励添加等,以极槽配合27/24的DDM为例,三维有限元模型如图3所示。

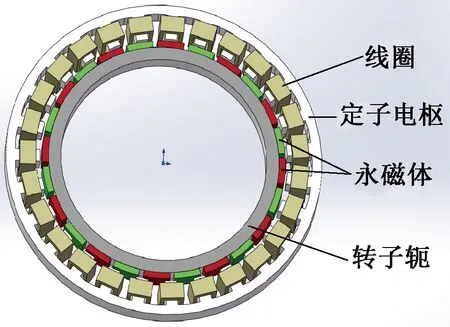
图3 27/24三维有限元仿真模型

通过Maxwell有限元仿真软件,对上述四种不同极槽配合的DDM进行仿真,将仿真后的结果进行分析。

3.2 齿槽转矩分析

齿槽转矩是永磁电机的固有特性,由于DDM通常直接与运动装置上,故齿槽转矩会一定程度上影响DDM定位精度,因此对DDM进行性能分析的时候结合齿槽转矩非常有必要。

4种极槽配合下DDM的齿槽转矩峰峰值如图4所示,分别为160 mN·m、151 mN·m、91 mN·m、153 mN·m。结果表明,极槽配合为27/28的DDM具有最小的齿槽转矩,并且具有较好的对称性,相较于其他3种极槽配合组合具有显著优势,能满足DDM应用于高精密仪器的要求。

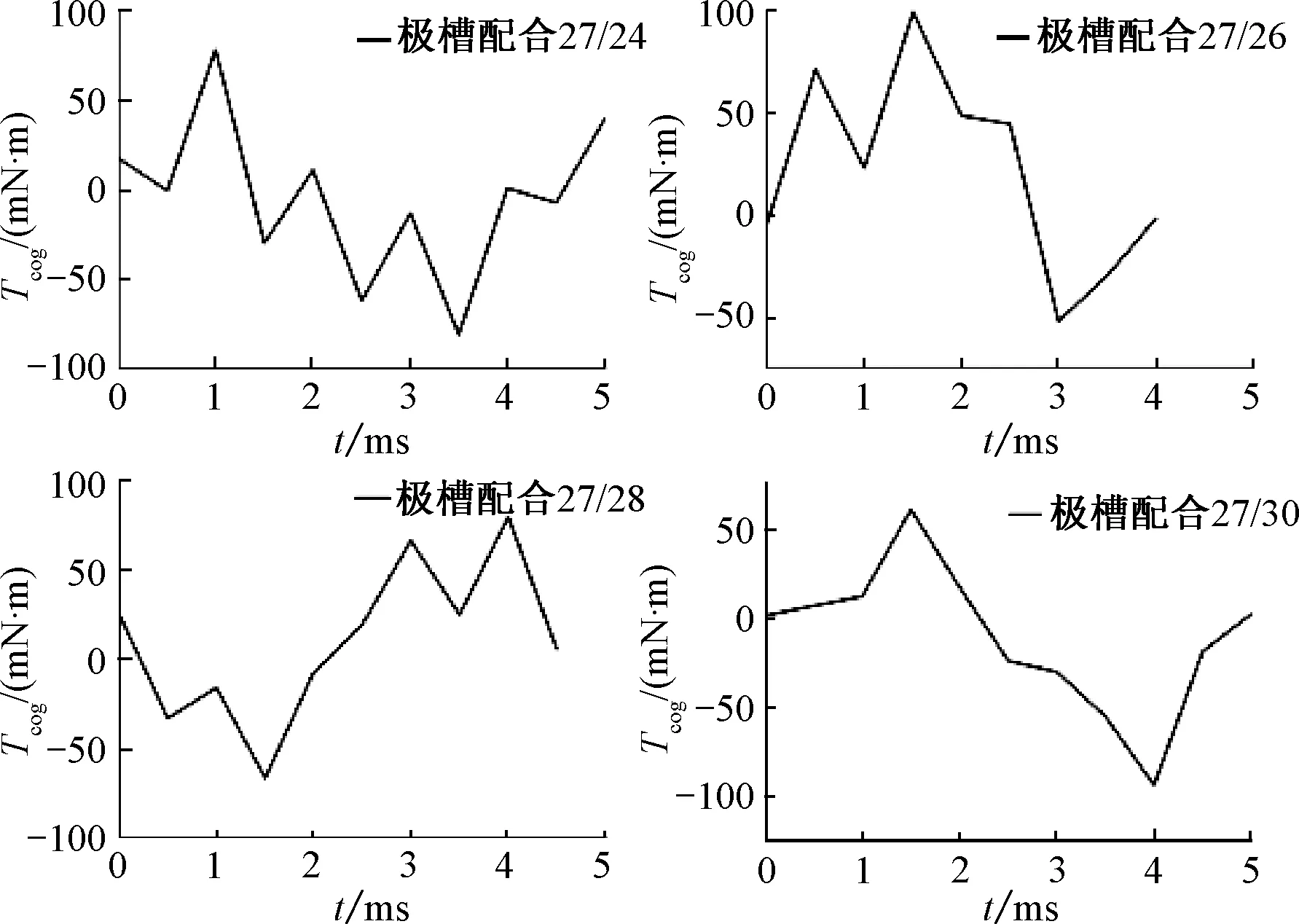
图4 4种极槽配合下的齿槽转矩

3.3 气隙磁密与反电动势分析

通过有限元仿真后,得到4种不同极槽配合下电机的空载气隙磁密,随后对其进行傅里叶分析,气隙磁密波形与傅里叶分析的结果如图5所示。

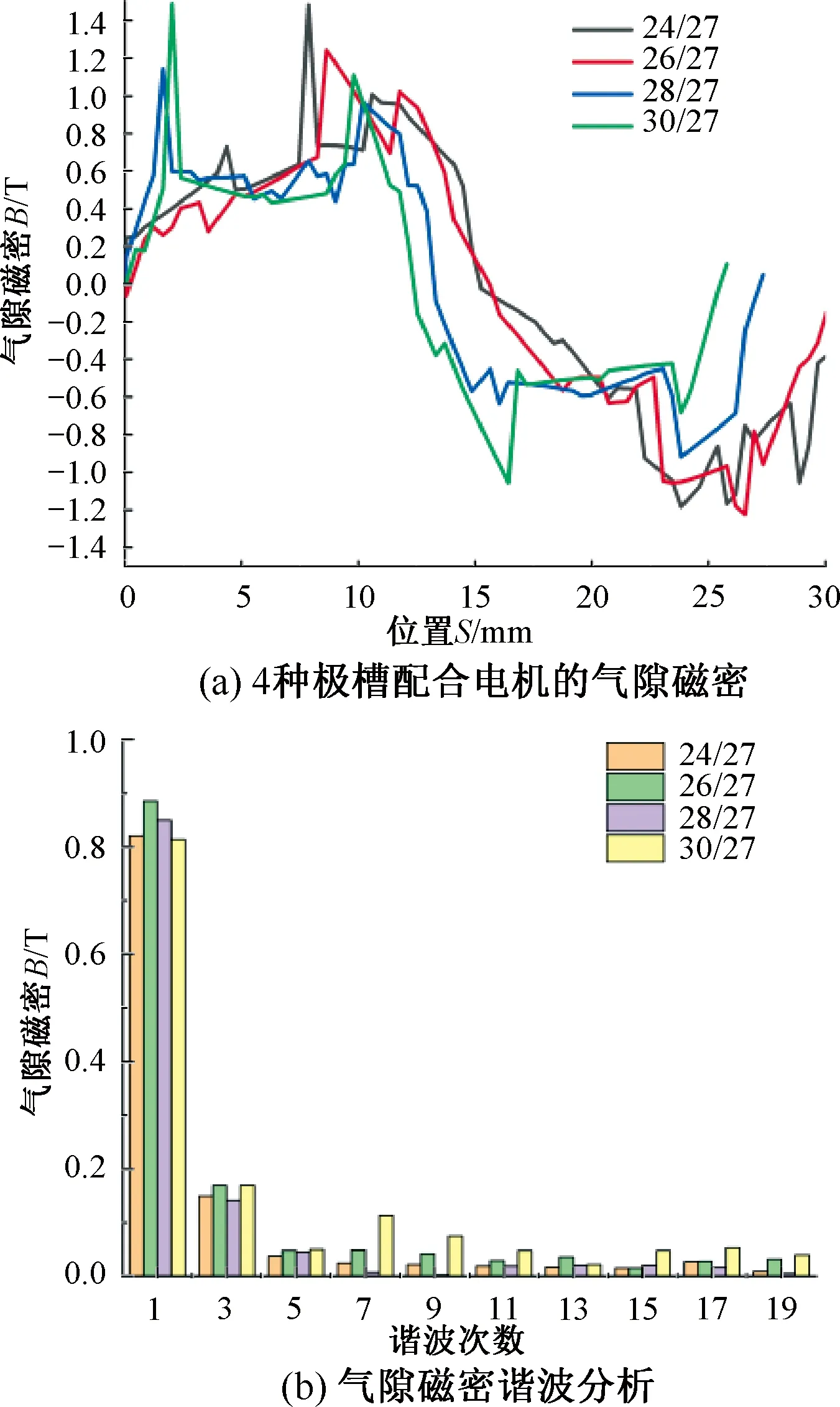
图5 4种极槽配合下DDM的气隙磁密

结合图5 4种极槽配合下电机的气隙磁密傅里叶分析图可知,4种极槽配合电机的基波气隙磁密幅值依次为0.82 T,0.885 T,0.85 T,0.813 T。可以发现,极槽配合为27/26与27/28两款电机的基波气隙磁密幅值相较于另外两款较大,其中各极槽配合的3次谐波气隙磁密幅值分别为0.15 T,0.169 T,0.142 T,0.169 T,分别占基波气隙磁密幅值的18.3%,19.1%,16.7%,20.8%,各极槽配合下的5次谐波气隙磁密幅值分别为0.038 T,0.048 T,0.045 T,0.05 T,分别占基波气隙磁密幅值的4.6%,5.4%,5.3%,6.2%,其余各奇数次谐波中极槽配合为27/28的幅值均为最小,27/26次之,27/30较差。此外,图5表明,极槽配合为27/28的DDM气隙磁密谐波含量最低,具有较好的波形,能为电机提供较好的气隙磁密,保证了电机的输出性能。

空载反电动势的波形畸变率反映出电动势中的谐波含量。通过有限元分析得到空载情况下的反电势波形如图6(a)所示,对图6(a)中的反电动势进行傅里叶分析后得到空载反电动势的傅里叶分解图如图6(b)所示。并对4种极槽配合下的DDM反电动势畸变率进行计算,计算公式如下:

图6 4种极槽配合下A相空载反电动势的波形及谐波

式中:U1为空载反电动势基波分量值;Un为空载反电动势各次谐波分量值。

由于空载状态下,反电动势是三相对称的,故取4种极槽配合下的A相反电势进行对比分析。从图6可以看出,在相同转速与相同匝数情况下4种极槽配合的反电动势基波幅值分别为26.7 V,28.4 V,28.5 V,28.7 V,其中空载反电动势的三次谐波值分别为0.953 V,0.592 V,0.55 V,0.534 V,其波形畸变率分别为3.9%,2.37%,2.52%,3.27%。极槽配合为27/28的DDM空载反电动势的奇数次谐波含量相较于其他3种极槽配合组合低,表明该极槽配合下的空载反电动势的波形畸变率较低,在同等情况下产生的损耗较少,符合DDM高性能、高效率的设计要求。

3.4 转矩脉动分析

为探究负载情况下的电机转矩脉动情况,对上述4种极槽配合的DDM进行仿真,将输入相同电流激励情况下的转矩脉动进行对比分析,引入转矩波动率来评价转矩的波动情况。转矩波动率定义:

式中:n为周期数;Tnmax、Tnmin分别为第n周期内的转矩最大值、最小值;Tavg为平均转矩;KT为转矩波动率。

如图7所示,结合仿真数据表明,4种极槽配合的DDM在输入电流为8 A的情况下转矩波动率依次为61.79%、8.23%、6.83%、12.04%,这表明在运行状态下,极槽配合为27/28的DDM具有较低的转矩脉动,能适用于定位精度较高的工作场景,同时能满足运行要求,具有明显的优势。

图7 4种极槽配合下的转矩波形

4 结 语

本文针对应用于数控机床的27槽DDM的极数进行初步选择,选择出极数槽数相近的4种极槽配合选择,结合齿槽转矩与绕组系数的表达式对上述4种极槽配合组合进行初步判断。对4种极槽配合组合的DDM进行建模与有限元分析,通过分析仿真结果表明,极槽配合为27/28 DDM的气隙磁密、空载反电动势谐波含量较低,同时具有较小的齿槽转矩和转矩波动,能够符合数控机床对定位精度与高性能的要求,为DDM在数控机床上的应用提供了一定的参考依据。