初中数学教学中数形结合思想的应用分析

贾龙才

【摘要】数形结合在课程教学中的应用比较普遍，且应用效果较好，可以助力于学生的知识理解，促进学生思维拓展的作用.初中数学课程教学中应用数形结合的思想，将数字、图形两个知识要素进行融合，可以准确、直观地表达出数学知识间的逻辑关系.文章对数形结合思想进行研究和分析，并对其在具体初中数学课程教学中的实践应用进行研究，提出了提高數形结合思想应用的措施.

【关键词】数形结合；初中数学；思维能力；数形互变

引 言

数形结合思想是一个比较广泛的概念，在该思想的引领下，教师对初中数学课程教学的应用灵活性有所增强，教学效果也进一步增强.数形结合思想的应用可以贯彻落实课程教学的各个阶段，所应用的方法也存在差异，在应用形式上可以与多媒体技术融合，建立数学模型，助力于学生对知识的理解，以符合对学生能力培养的目标.

一、数形结合思想的应用方法

数形结合思想在初中数学课程教学中的方法应用上，教师应充分考虑到数字与图形之间的关系，判断二者之间的内在联系.具体而言，教师将数形结合思想应用在教学中，可以采用以形促数、以数解形、数形互变的方法.

（一）以形促数

针对初中数学课程中比较复杂的内容，如抽象化的数量关系，教师可以应用图形的方式将其直观展现，学生在解题过程中根据图形之间的联系解决复杂的数量关系问题.教师再次应用以形促数的方式，对函数关系进行讲解，帮助学生更加直观地了解数学问题.

以初中数学“一次函数”的课程教学为例，列出一次函数“y=ax+b”，其中a，b两个数值均为常数，且a不为0.教师如果直接对数量关系进行解释，那么学生很难对其进行理解，教师如果将数量关系绘制成为直观的图形，那么学生对知识内容的理解将会更加深入.因此，教师可以在黑板上列出不同情况下的图形，解释一次函数中的数量关系（如图1）.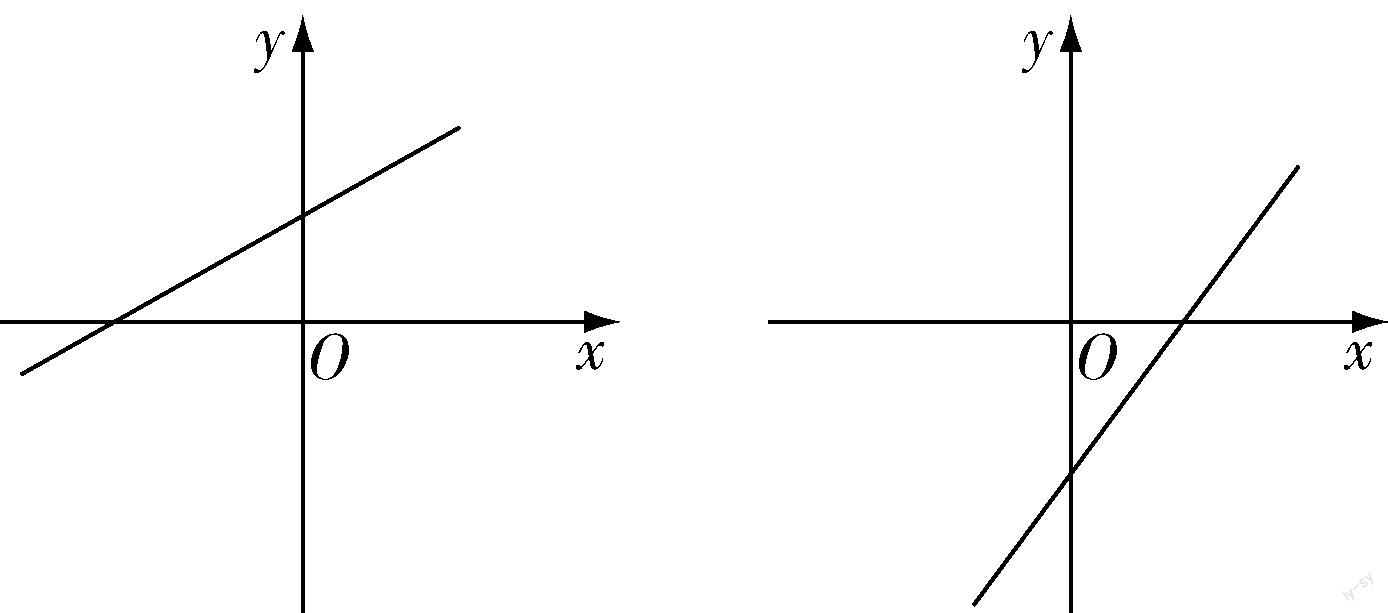

教师将原本抽象的数量关系以图形的方式展示在黑板上，使学生对一次函数的数量关系有了更加深入且直观的理解.教师根据图形和一次函数的性质，设置例题“y=2x2+6”，在图像中存在两个点，分别为（2，y1），（-2，y2）.学生按照教师所应用的数形结合思想进行习题解析，将数量关系带入函数中，对其进行比较和分析，判断y值的变化关系，最终得出答案.

以形促数方法的应用是依据数形结合的思想对相关问题进行解析，将原本复杂的数量关系以图形的方式直观展示出来，并根据设置的不同条件，绘制成不同的图形，通过对图形的分析，直观地了解习题中的数量关系.

（二）以数解形

以数解形是指利用数量关系对图形内容进行解析，采用定量计算的方式对一些复杂的图形进行条件展示，将题型中隐藏的条件进行论述，实现对图中相关内容的计算.该类方法应用在几何图形解析中应用比较常见，可以挖掘题型中无法直观展示的隐藏条件，对具体的关系进行解析.例如，在几何图形的解析中，采用以数解形的方式开展教学活动（如图2）.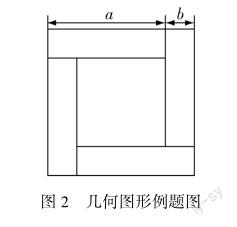

条件：图形中的四个长方形为全等长方形，由四个长方形组成上述图形，中间空白区域根据已知条件列出等式.

教师在此类题型的教学活动中，充分利用数形结合思想，采用以数解形的方式对习题进行解析.考虑到四个长方形全等，因此中间区域为正方形，其边长可以利用数量关系进行计算，即用（a-b）表示.根据正方形面积的计算公式，中间空白区域的面积为（a-b）2.根据已知条件列出恒等式（a+b）2-4ab，即可得出中间空白区域的面积.因此，（a+b）2-4ab=（a-b）2为最终的恒等式.

（三）数形互变

教师应用数形结合思想对数量与图形之间的关系进行表达，将数量关系与图形进行灵活转化，根据已知条件计算最终结果，得出最终的结论.该方法应用数形结合思想将数量关系与图形之间的关系进行转化，在几何图形表达计算习题中的应用具有可行性（如图3）.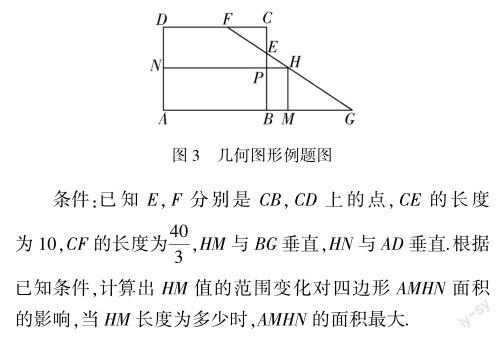

在解题过程中，根据已知条件，将HM的长度设为x，AMHN的面积大小设为y.根据已知条件列出等式，并根据等式衡量图形各边长与面积之间的关系.通过数形互变的计算方式，最终得出结果，当HM的长度为30，可以计算长方形的面积值的最大值为1200.解题过程中同时利用数量关系和图形对已知条件进行转化，将所列出的数量关系绘制成二次函数图像，并在图像中根据取值范围计算HM的最大值，从而取得面积的最大值.

二、数形结合思想的应用形式

（一）以多媒体技术为载体的数形结合思想应用

多媒体在初中数学课程教学中被广泛应用，教师在深化教学改革的同时，积极探索数形结合思想与多媒体信息技术的融合应用方式，并不断对其进行创新应用.根据数形结合中的两大要素，教师可以利用多媒体设备挖掘资源，使得数形的转化过程更加直观、清晰，教学质量与教学效果可以满足要求.多媒体的动态化展示功能也为数形结合思想的应用创造了良好条件.

例如，在“几何图形”的课程教学中，当涉及圆的课程时，教师可以将数形结合思想与多媒体技术充分融合，利用电脑的绘图软件在画板上绘制出圆形，当涉及相交线或者平行线时，教师可以动态对其进行绘制，并在此过程中对知识内容进行解析.利用多媒体设备将知识内容进行分解，使得教学更加直观.教师通过多媒体设备的动态演示功能应用，使学生更加深入地了解几何图形的平行关系与位置关系，可以点击鼠标拉长或者对位置信息改变，两条线始终处于平行的状态下.教师利用“形”的多元动态变化对数量关系、性质等知识内容进行解析，有效地提高了学生的空间想象力.因此，多媒体与数形结合思想相结合的应用可以发挥良好的作用，既可以进一步将知识点直观化，又可以进一步深化学生对知识内容的理解程度，空间几何思维能力也得到一定程度的提高.

（二）以数学模型为载体的数形结合思想应用

数学模型建立是数形结合思想中“形”的部分，由于课程教学目标指出，初中数学教学不仅要传递学生数学知识，而且应该注重学生解题能力的提高，吸引学生主动参与学习，主动解决难题，掌握数学规律.教师将数形结合思想应用到课程教学，并通过建立简单的数学模型的方式对数学逻辑关系进行表达，符合初中生心理发展目标，可以增加学生对知识的理解程度.例如，初中数学课程中涉及“数轴”的教学中，教师利用数轴点表达有理数的关系，并明确数与数轴之间的对应关系.部分学生由于基础比较薄弱，数学逻辑关系较差，所以在对应关系的学习过程中存在一定的难度，难以保障教学质量.因此，教师应用数形结合思想建立数学模型，绘制若干个具有包含和被包含关系的圆圈，圆圈中包括有理数、分数、整数、非整数、正数等.当数学模型建立完成后，学生们对数字之间的逻辑关系理解会更深入.在数学模型绘制过程中，教师采用引导的方式引发学生思考，与学生进行有效互动，或通过讲故事的方式建立数学模型，学生的趣味性、参与度也在一定程度上有所提高.因此，教师应尝试应用数学模型的方式对学生渗透数形结合思想，实现对知识内容的渗透与解析.

三、数形结合思想应用理念

（一）课程导入设计

数形结合思想在初中课程教学中的应用体系已经趋于完善，在不同的教学阶段应用方式也很好.教师在课程导入阶段应用数形结合思想，可以为后续的课程教学奠定良好的基础，提高学生基础知识能力的应用.在课程导入阶段，教师利用数形结合思想可以吸引学生的注意力，勾起学生的好奇心，整节课的教学氛围将会变得十分良好.例如，在“三角形的内角和与外角和”的课程导入阶段，教师可以应用数形结合思想对三角形的相关定理进行导入，包括直角三角形、钝角三角形、锐角三角形的角度关系.教师应用多媒体设备将三种三角形绘制在画板上，要求学生根据绘制的图形，讲述自己的认知，使得学生了解不同类型三角形的内角关系大小不同，即直角三角形兩个锐角互余、外角互补等.在课程导入环节应用引导式、问题式或者趣味性比较浓厚的教学导入方式，通过列出图形的方式明确各角度的数量关系，学生对知识的学习情绪、课堂投入程度将会有所增加.因此，教师应善于将数形结合思想应用到课程的导入环节中，挖掘数形结合思想在课程导入阶段的应用理念，营造良好的教学氛围.

（二）教学环节应用

在问题导入阶段结束后，教师需要步入正题，对知识内容进行探究，使得学生在探究的过程中了解知识、应用知识，实现情感目标、能力目标同时渗透.数形结合思想在教学环节的应用可以深化学生对数学知识的理解.例如，在“几何图形”的课程教学中，教师可以应用数形结合思想解决相关问题，引导学生对知识进行探究.在讲解“几何图形”的面积时，教师可以要求学生利用相关的工具在笔记本上绘制图形，理解几何图形的边长关系，并对面积进行计算.针对一些不规则的几何图形，学生们在绘制过程中通过增加边线、分割等方式，将其分为若干个规则的图形，再对其面积进行计算.教师在课堂教学中发挥着对学生探究引导的作用，引导学生如何应用数形结合思想解决相应的问题，更好地帮助学生厘清图形与数量之间的逻辑关系，采用线条分割、增加线条等方法对图形进行重构，解决相应的难题.因此，在课堂教学中，教师要认识到数形结合思想对于解题的重要意义，引导学生掌握用数形结合思想解题的方法.

（三）教学理念深化

数形结合思想在教学领域中的应用可以起到升华主题、拓展知识、升华教学理念的作用.考虑到初中数学有很多知识对于学生而言存在一定的学习难度，导致学生的学习效果较差.因此，教师可以利用数形结合思想开展教学活动，渗透新型的教学理念，对课程的核心内容进行深化，使得学生的知识结构更加全面，基础能力更加夯实.例如，在“二元一次方程”的课程教学中，教师可以采用以数解形、以形促数等方式，将原本的图形与数量关系进行灵活地转化，不仅可以提高学生的图形空间思维能力，而且对学生的计算能力也有一定程度的提高.在具体教学中，考虑到学生个体知识结构的差异性，教师可以应用分层教学理念、分级教学理念、个性化教学理念，并利用数形结合思想对学生进行渗透，将新型的教学理念与课程内容教学有效融合.针对学生空间思维能力比较弱的学生，教师可以应用数形结合思想重点提高学生的图形思维能力，针对解题能力较弱，数量逻辑关系较弱的学生，教师可以应用数形结合思想重点提高学生的数学逻辑，实现教学理念的进一步升华，在开展教学的同时，使学生对知识内容进行深入拓展.

（四）教学目标制订

初中数学课程教学重点目标在于能力目标、情感目标的设定，而知识目标的渗透是在以上两个目标建立的基础上开展的，这更加突出了学生在课程学习中的主体地位.以学生数学思维能力为目标的数形结合思想渗透和以学生学习趣味为目标的数形思想渗透所采用的教学方法不同，教师应不断探索不同的教学目标与数形结合思想融合的可行性.例如，在“相交线与平行线”的课程教学中，教师可以应用数形结合思想渗透以培养逻辑思维能力为目标的课程教学活动.相交线与平行线之间的关系，相交线与平行线之间的不同，教师均可以应用数形结合思想进行渗透.通过绘制图形的方式对二者进行对比.在“几何图形”的课程教学中，教师可以渗透以培养学生空间想象能力、数学感知能力为目标的教学活动，通过数形互变的方式明确几何图形中的数量关系与图形关系，使得学生对知识的感知更加直观和具体.初中数学课程教学在渗透数形结合思想的同时，应将教学目标与之结合，按照人才培养方案、教学纲要等文件要求，对数形结合思想进行应用，以更好地挖掘数形结合在人才培养中的应用潜力与应用价值.

（五）知识应用渗透

教师在传递知识的同时应重点提高学生的知识应用能力，可以将所学的知识应用到生活解题中，解决生活中的难题.基于此，教师可以挖掘多媒体技术在数形结合思想中的应用价值，重点培养学生的知识应用能力.例如，在“三角形的内角和与外角和”的课程教学中，教师可以挖掘生活资源，结合数形结合思想进行知识教学.教师可为学生设置生活化问题，如果一块三角形玻璃被打碎，而他的底边呈现出平直的状态，侧边形成两个向内延伸的边，但并未交叉，如何将其恢复成为完整的三角形玻璃.学生们开始尝试应用拼接法、组合法、镶嵌法等解决教师提出的问题，在此过程中学生对三角形知识的应用能力也有所提高.因此，教师应注重对学生知识应用能力的提高，渗透数形结合思想，引导学生将知识应用到生活解题中.

结 语

综上所述，数形结合思想的在初中数学教学中的应用具有灵活性，在方法、方式、理念渗透上的应用均具有可行性，且可以有效提高课程教学质量，满足课程教学目标.初中数学教师在应用数形结合思想的同时，要进一步探索数形结合思想应用的可行性、适用性，创新应用手段，丰富应用方式，使其可以发挥培养学生能力的目的.

【参考文献】

[1]王先贵.数形结合在小学数学教学中的应用研究：以小学数学“图形与几何”教学为例[J].当代家庭教育，2022（06）：4-7.

[2]陈涛.在转换中化难为简：浅析数形结合思想在高中函数教学中的应用途径[J].考试周刊，2022（02）：56-59.

[3]陈艳琼.数形结合方法对初中生思维能力培养的重要性及实施策略研究[J].考试周刊，2022（01）：9-12.

[4]陈永畅，赖允珏.从教材的视角审视数形结合的内隐价值：以数线图、点子图和矩形图在数与代数中的应用为例[J].小学教学（数学版），2021（12）：26-28.

[5]沈爱平.经由数学思想，走向核心素养：以数形结合思想的教学为例[J].数学教学通讯，2021（32）：43，82.