初中生“数学求知欲缺失”现象及其教学对策

陈伟华 黄贤明

摘要：随着学生步入初中，数学学习难度不断增大，数学求知欲缺失现象愈发明显。造成这种现象的原因，涉及数学学科、教师教学与学生学习三个方面。对此，基于数学求知欲的产生、发展过程，提出三条教学建议：夯实数学基础，为求知欲的唤醒奠基；探究未知问题，为求知欲的发展铺路；增添人文趣味，为求知欲的维持供能。

关键词：初中数学；求知欲；数学基础；问题启发；人文趣味

一、问题提出

作为一种心理动机，求知欲是每个人与生俱来的特性。当人们在生活或学习中遇到感兴趣且未知的信息，并且不能在已有知识结构中找到匹配的解释时，就会产生一种心理失调，萌发要解决这种失调心理状态的行为，表现出探求知识的欲望。

苏格拉底将“强烈的求知欲”作为向他学习知识的首要条件。苏霍姆林斯基曾说：“哪里没有求知欲，哪里就没有学校。”求知欲对于人当下及未来的学习与发展都有着举足轻重的作用与意义。

作为初中数学教师，我们常常思考“如何让学生理解数学知识？”“如何提高教学效率？”“如何激发学生的数学学习兴趣？”等问题，并积极向各种文献或经验丰富的教师“取经”，这是作为教师在“终身学习”中求知欲的体现。但我们所面对的初中生在数学学习中却越来越缺乏求知欲。很多学生对数学学习逐渐失去兴趣，被动地接受数学知识，进而表现出对未知的数学现象、常见的数学问题、新的数学知识的漠视。即便是一些学习成绩处于中上等水平的学生，也很难主动去探索数学问题，发现数学知识。尤其是，很多学生在没有考试要求的内容或者拓展内容的学习中表现出不认真、无所谓等态度。随着学生步入初中，数学学习难度不断增大，这种现象愈发明显，既阻碍了学生的数学学习与发展，也消磨着教师对数学教学的热情。

那么，造成学生数学求知欲缺失现象的深层次原因是什么？数学教学中，如何培养学生的求知欲？

二、成因剖析

数学教学是师生双方围绕数学学科相互作用的过程，学生数学求知欲缺失现象是数学学科、教师教学与学生学习三者共同作用的结果。下面，就从这三个方面着手剖析其成因。

（一）数学学科方面

数学是研究数量关系和空间形式的科学，其研究对象源自对现实世界的抽象。［1］在初中阶段，数学学习内容的抽象程度和复杂程度大大提高。以数与代数领域为例，小学阶段的学习内容侧重于数与运算、数量关系，而初中阶段随着数系的扩充和字母表示数的引入，学习内容变为数与式、方程与不等式、函数，更要求学生以动态（变量）的眼光观察数学世界。此外，在数学核心素养方面，初中阶段更强调抽象能力、模型观念和推理能力。抽象程度越来越高，让数学学习内容（特别是考试题目）越来越脱离生活现实。这对学生学习提出了更高的要求，让不少能力一般的学生逐渐产生畏难心理，并且随着学习的深入，而主动知难而退，最终导致数学求知欲缺失。

（二）教师教学方面

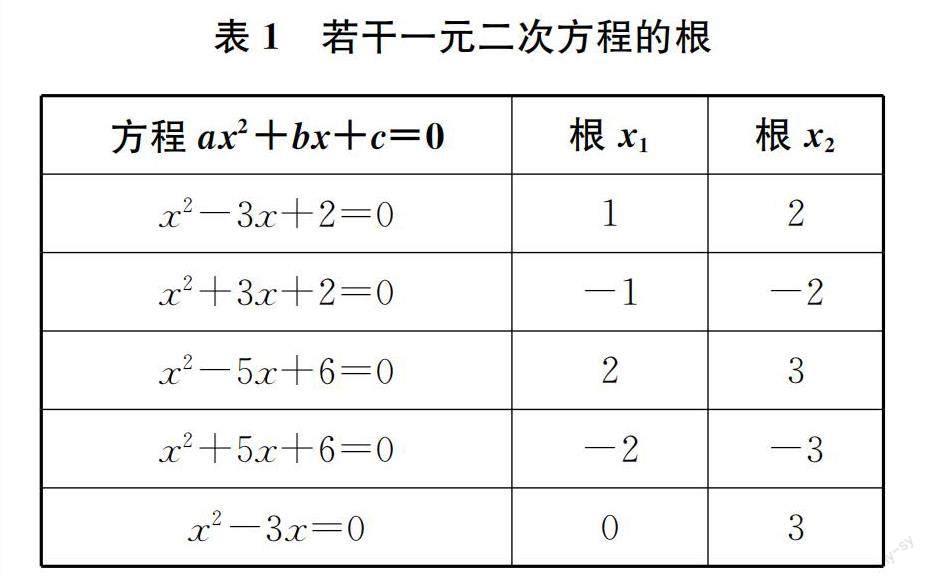
一些教师的教学缺乏引导性、启发性、趣味性、人文性等，长期处于一种“为我”的状态，而弱化了学生在课堂中的主体地位，其主要表现在问题的设计方面。［2］“问题是数学的心脏”，在数学教学中的地位不言而喻。而一些教师为了追求教学的“效率”，增加学生练习的时间，只围绕知识内容设计问题，致使问题大多是封闭的或半封闭的，对学生的引导性、启发性不强，难以激发学生的好奇心与求知欲。以韦达定理的教学为例，若教师参照苏科版初中数学教材提出问题：观察表1，你能发现其中一元二次方程的根与系数有什么关系吗？学生就会产生困惑：已经学过求根公式，为什么还要探究根与系数的关系呢？即问题未让学生获得学习新知的必要性。此外，一些教师常常淡化数学课堂中的趣味元素与人文元素，如数学游戏、数学欣赏、数学史、数学文化等，或以大段文字的形式呈现资料，看得学生“眼花缭乱”。这些都会让学生逐渐产生“数学枯燥无味”的看法，消解数学求知欲。

（三）学生学习方面

学生是学习的主体。数学求知欲缺失现象的产生主要源于：学生在思想上对数学学习不主动；在数学学习中遭遇过多的挫折而产生习得性无助行为；缺乏观察世界的数学眼光、思考世界的数学思维、表达世界的数学语言，难以从现实世界中发现与提出问题、分析与解决問题。第一点，主要是在“唯分数论”“唯结果论”的影响下，学生迫于教师、家长和考试的压力而不得不学习数学，处于“要我学”而非“我要学”状态，自然对数学学习不感兴趣。第二点，主要是受限于自身认知水平、学习能力、学习习惯等因素，或在小升初后不适应初中阶段的学习，在数学学习中经常遇到不理解的知识、难解决的问题、不佳的成绩等，学生不断消磨着数学学习的热情。第三点，主要是在数学学习中，学生只关注知识的习得，而忽视知识背后的渊源，目光局限于课本、习题，长期在虚构的生活情境中机械化地应用数学知识，从而逐渐失去了用数学眼光观察现实世界的兴趣，发现数学元素、提出数学问题的能力也不断退化，数学求知欲自然有所消解。

当然，造成学生数学求知欲缺失现象的原因还有很多，如家庭教育、班集体的学习氛围等。

三、教学对策

面对普遍存在的学生数学求知欲缺失现象，教师需要有计划、有目的地改进自身的教育教学方式，在潜移默化中激发学生的求知欲，并长期保持。

数学求知欲的产生，离不开两方面的因素：一是在生活或学习中遇到未知的数学信息，并且与自身内在的知识结构产生冲突；二是对数学学科有一定的兴趣。进一步结合数学教育研究来看数学求知欲的产生、发展过程，首先，学生需要有知识与经验的积累，包括必要的能力与素养、良好的习惯与态度作为基础；其次，在这些基础之上，学生通过对现实世界的观察与抽象、对数学的自主探究与反思以及教师指向知识生长的启发性问题这三条路径，获得具有探究性的数学问题，从而产生内在的认知冲突，激发求知欲；最后，在求知欲的驱动下，学生经历数学问题的探究过程，进一步完善知识与经验体系，发展数学核心素养等。同时，数学学习兴趣贯穿这一过程的始终，是数学求知欲产生的催化剂。而这个过程也构成一个循环（如图1所示）：求知欲的产生最终服务于学生的数学学习，这些习得的知识与经验等都将成为新一轮循环的开始。这也反映出求知欲是学生数学学习道路上源源不断的动力。

由此，可以提出三条教学建议：

（一）夯实数学基础，为求知欲的唤醒奠基

初中生经历了小学六年的数学学习，但由于个体差异以及教师教育理念、教学方法的差异，他们掌握的“四基”“四能”及其程度，形成的数学核心素养、数学品格，养成的数学学习习惯与态度等都有不小的差异。求知欲的唤醒是建立在一定的知识与经验等基础之上的。如果谈及某个数学知识，学生完全无法在认知结构中提取相关的记忆或在生活经验中找到类似的信息，那么他将处于一种迷茫的状态；即便教师的问题充满启发性与引导性，他也无法产生探索该知识的欲望。也就是说，这时学生即使踩在了教师所搭的“脚手架”上，也不能“垫个脚”或“跳一跳”而达到学习目标。因此，教师要关注学生整体的情况，立足学生的“最近发展区”，适当降低教学目标，让大部分学生都能较为轻松地达成。在夯实学生“双基”的同时，逐渐指向“四基”“四能”与数学核心素养的发展。当然，教师在日常教学中，还需进一步教会学生初中数学的学习方法，引导学生养成良好的数学学习习惯，包括记录与整理、订正与反思、检查与验证等。最终，在扎实的数学基础、良好的学习习惯等因素的共同作用下，学生的数学求知欲将不断被唤醒。

（二）探究未知问题，为求知欲的发展铺路

陶行知先生在《每事问》一诗中写到“发明千千万，起点是一问”，指明了创造性活动的起点是问题提出。若没有问题，就无法生成疑难、困惑等心理，更不会激发探究的欲望。学生在一定的知识与经验等基础之上，需要问题来引发认知冲突，进一步激发数学求知欲。数学问题来源于以下三个方面：

1对现实世界的观察与抽象

数学为人们提供了一种认识与探究现实世界的观察方式、一种理解与解释现实世界的思考方式、一种描述与交流现实世界的表达方式。［3］学生拥有了一定的数学知识与经验，自然会以数学的眼光发现生活中的数学现象，提出相关的数学问题，并激发起探究问题的求知欲，希望用数学的语言、思维加以解释、解决。例如，有学生从出租车计费这一真实生活场景出发，提炼出“出租车计费与行驶里程存在什么关系？”“乘客采用分乘两次的方法能降低乘坐出租车的费用吗？”这两个问题，并构建函数模型加以解决。［4］因此，教师在教学中要积极创设真实的生活情境，促使学生经历用数学的眼光观察现实世界的过程，培养学生的问题提出能力，激发学生的探究欲望。此外，现行义务教育数学课程专门设置了“综合与实践”这一学习领域。在初中，教师可依托综合与实践活动，采取项目式学习的方式，引导学生通过数据收集、观察思考、操作体验等活动，经历数学信息的获得过程，再通过对所获信息的进一步分析与讨论，提出所需解决的问题。在问题解决的导向下，学生的求知欲将进一步被激发，促使他们积极地找寻相关的资料（包括其他学科的知识与思想方法），进而解释与解决问题。例如，教师可以围绕“概率与统计”内容设计“身边的概率与统计”项目，引导学生研究抛硬币、抛骰子、转转盘等游戏在现实生活中与理论情况下的差异，鼓励学生勇于质疑，进而以“疑”激“欲”。［5］

2对数学的自主探究与反思

除了现实世界中的数学问题，在数学内部的发展中也能提出许多问题，主要包括两类。其一，学生在一定的思维范式下，根据一些直观现象推测出新的数学知识，进而对其正确性产生疑问。例如，学生在学完“两直线平行，同位角相等”后，会产生“两直线平行，内错角是否相等，同旁内角是否互补？”的疑问，进而激发出探究欲望。其二，学生在整理知识时，发现了一些知识的“留白面”，产生对其外延的好奇。例如，学生在学习无理数概念时，感受到面积为2的正方形边长是无限不循环小数，也能推理出正方形的面积为3、5、7等数时边长也是无理数，就会产生“如何表示这些无理数？”的疑问，进而询问教师或查询资料来满足自己的求知欲。不难发现，此类问题的提出对学生的自主学习能力有较高的要求，需要教师在日常教学中有意识地关注与培养。教师可以时常给出一些类似的问题来“抛砖引玉”，引导学生的思考与探究，以此一轮又一轮地“激发—满足”学生的求知欲，让求知欲与数学学习相互促进、共同发展。

3指向知识生长的启发性提问

大部分学生主动提出问题的能力还有待提高，他们更习惯于被动地接受问题。因此，教师提出的问题更应具有引导性与启发性，既要让学生感受到学习该内容的意义，又要很好地激发学生探究该内容的欲望。以韦达定理的教学为例，教师可以设计“求方程x2＋273x－550＝0的两根之和，在求解的过程中你有什么感受？”和“求根公式还便于求解吗？你有其他方法求两根之和吗？”这两个问题，让学生感受到求根公式“失效”，从而形成强烈的认知冲突，构建韦达定理的学习意义，产生对“根与系数新关系”的求知欲。［6］

（三）增添人文趣味，为求知欲的维持供能

“兴趣是最好的老师”，学习兴趣也是维持求知欲源源不断的能量。数学学习兴趣的培养应该关注以下三个方面。其一，教师作为学生的榜样，要严慈相济，既严格要求学生的数学学习规范，又私下关心学生的数学学习状态，只有让学生“亲其师”，学生才能“信其道”。其二，教師要关注数学课堂人文趣味的渗透，包括课前小游戏、数学文化介绍等。例如，在苏科版初中数学七年级下册《证明》单元复习课前，教师可以组织“谁是卧底”的游戏，“卧底”与“平民”的语句分别是“两直线平行，内错角相等”“内错角相等，两直线平行”，让学生在游戏中回顾真命题、互逆命题、平行线的性质与判定等知识，让数学变得有趣起来，很好地调动课堂氛围。其三，教师要形成文化作业观，布置开放性、探究性、操作性的数学作业，让学生在作业完成中进一步感受数学的美妙。例如，《七巧板》一课，教师可以布置实践性作业：（1）制作一副七巧板，并用它拼出自己喜欢的图形；（2）通过查阅资料，了解四巧板、五巧板、九巧板等，选择其一，制作一副“巧板”，并拼出自己喜欢的图形。该作业有效发挥了“巧板”的文化价值，激发出学生对“巧板”学习兴趣，充分调动了学生探究的主动性，促使学生在临摹“巧板”、拼搭“巧板”中，发展“创造美”的能力。［7］总之，在数学学习兴趣的培养下，学生对数学的求知欲才会不断维持，最终成为受益终身的“宝藏”。

综上所述，教师要摸清学生数学求知欲缺失现象的深层次（个性化）原因，认真研究数学教学内容、数学教材，改进自身的教学方式，努力让课堂变得内涵丰富、启发性强、生动有趣，并且有意识地培养学生良好的数学学习习惯，纠正不良的数学学习态度，让学生在“四基”“四能”的基础上，逐步发展数学核心素养，尽可能帮助学生实现“爱问乐学”，达到“勇于探索”。

参考文献：

［1］［3］中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：1，56.

［2］毛锡荣.数学教学中“懂而不会”现象的成因剖析与对策研究［J］.数学通报，2022（2）：3134.

［4］张乐天，李沅骏，孙凯.出租车收费问题探究［J］.中学数学月刊，2022（5）：75＋79.

［5］徐斌艳，等.数学素养与数学项目学习［M］.上海：华东师范大学出版社，2021：214228.

［6］黄贤明.基于5E教学模式的“一元二次方程的根与系数的关系”教学设计与思考［J］.数学通讯，2022（7）：36.

［7］黄贤明.数学学科美育：内涵、价值与实现路径［J］.中学数学杂志，2022（12）：58.