基于Kirchhoff近似与曲面三角形网格的水下目标声散射特性分析

薛亚强,彭子龙*,俞强,张春雨,周富霖,刘进伟

(1.江苏科技大学 能源与动力学院, 江苏 镇江 212000; 2.上海海事大学 海洋科学与工程学院, 上海 200135;3.上海交通大学 海洋工程重点实验室, 上海 200240)

0 引言

水下目标声散射特性分析是水声领域的热点问题,也是实现目标探测和识别的前提,具有重要的理论价值和实际意义。对于形状比较规则的目标,如球、无限长圆柱等,其声散射特性可用解析法[1]求得。当目标的几何形状比较复杂时,一般采用数值解法,如有限元[2]、边界元[3-4]和将二者结合的耦合方法[5]等,以及T矩阵法[6]、时域有限差分法[7]、板块元方法[8]和声束弹跳法[9]等近似解法。

基于Kirchhoff近似的板块元方法最初用于雷达散射截面的计算,自引入水下目标声散射研究以来,广泛应用于大尺度模型的高频回波特性预报[10]。板块元方法的核心算法是通过傅里叶变换积分或Gordon积分[11]将面积分运算转化为代数运算;该方法的基本原理与直接数值积分方法[12]相似,将目标表面划分为若干网格,对所有网格的散射声场求和得到目标总散射声场。

Hiptmair等[13]采用Trefftz间断Galerkin方法和局部细化网格研究了软边界散射体的声散射问题。Chaillat等[14]将边界元方法和自适应网格用于求解复杂形状目标声散射,具有较高的收敛速率。文献[15-16]基于Kirchhoff近似对水下目标的高频声散射特性进行了研究,采用平面三角形单元离散目标表面。然而,对于表面曲率较大或形状较为复杂的目标,如含有多个子结构和不规则曲面的水下航行器,若采用平面单元进行网格离散,需划分大量的网格才能较准确地拟合目标外形。与平面网格相比,曲面网格可以更精确地逼近目标的几何形状。Wu等[17]采用曲边四边形及曲边三角形单元离散圆板及开口圆柱壳,建立了目标辐射与散射的边界元分析模型。Foote等[18]基于曲面网格模型对比了Kirchhoff近似与边界元得到的目标强度,并指出高频时二者的结果基本一致,但前者具有更快的计算速率。Venås等[19]采用高阶样条曲面单元和等几何边界元建立了潜艇的声散射分析模型。

本文基于Kirchhoff近似和曲面三角形网格建立了水下目标收发合置声散射特性分析模型,采用高斯-勒让德求积方法对面积分进行直接数值计算。以刚性球、椭圆柱、球冠柱和Benchmark缩比模型等为例,比较了Kirchhoff近似模型与其他方法的计算结果,验证了本文方法的准确性与高效性。

1 Kirchhoff高频近似

由物理声学方法或Kirchhoff高频近似可以得到收发合置时,刚性目标的散射声场势函数满足的Helmholtz积分公式[8]为

(1)

式中:k为波数;A为任意振幅;积分面S0为散射体的几何亮区表面;r为面元dS到收发合置换能器M的距离;θ为入射声线r与面元单位法向矢量n的夹角。如图1所示,r0为换能器M到参考点的矢量,rs为面元dS到参考点的矢量。

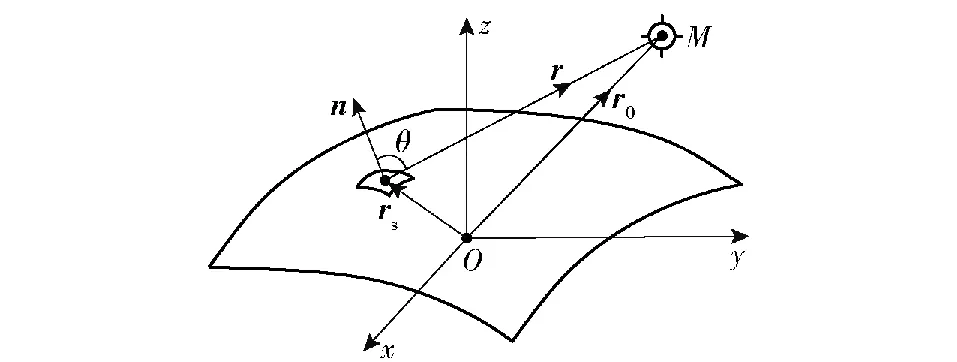
图1 Kirchhoff近似积分方法的坐标示意图

远场条件下,式(1)中被积函数的指数上取r=r0+Δr,r0为换能器M到参考点的距离,Δr为声程差,式(1)分母上取r≈r0,可得

(2)

将远场中的声线r与r0看作平行,声程差近似为Δr≈rs·r0/r0。式(2)中的积分可表示为

I=∬S0e2ikrq·r0/r0n·r0/r0dS

(3)

目标位置处的入射波势函数φi(r)=-(A/r0)·eikr0,由定义可得目标强度为

(4)

2 基于曲面单元的目标强度计算方法

首先对散射体的几何表面进行网格划分,离散为N个网格,然后按入射波是否直接照射将网格分为亮区和影区,最后对亮区内所有网格单元的散射声场求和,即可得到目标散射声场的近似值,由式(4)可得目标强度为

(5)

式中:Ii为第i个单元上的面积分。本文采取的网格类型为六节点曲面三角形单元,并建立了曲面单元上积分Ii的数值计算方法。

2.1 曲面三角形单元

考虑图2(a)所示的参数三角形单元,该单元由参数坐标(s,t)中的6个节点(Ai)定义,则图2(b)中曲面三角形上的点Q可表示为

图2 参数三角形与六节点曲面三角形之间的映射

(6)

式中:Bi为曲边三角形的顶点;Ri(s,t)为插值函数[20],简写为Ri,定义如下

(7)

曲面三角形单元上的积分Ii为

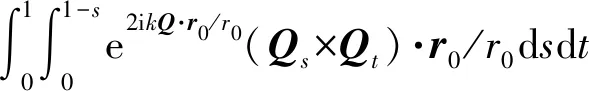
(8)

式中:Qs、Qt分别为点Q在s、t两个参数方向上的偏导数,

(9)

(10)

Ri,s与Ri,t为插值函数的偏导数,Be为曲面三角形单元6个顶点的坐标,分别表示为

(11)

(12)

Be=(B1,B2,B3,B4,B5,B6)T

(13)

2.2 高斯-勒让德积分

采用高斯-勒让德求积方法,可将式(8)中三角形区域上的积分表示为

(14)

式中:(ξj,ηj)为积分节点;n为积分节点个数;wj为权重系数。一般地,可将积分区域从三角形[0, 1]×[0, 1-s]映射到正方形[-1, 1]×[-1, 1],作参数变换:

(15)

式中:ξ与η为参数坐标,参数变换对应的雅可比矩阵为

(16)

将式(8)中的积分映射到正方形区域上,表示为

(17)

3 数值算例及分析

首先对散射体表面进行几何建模,然后将模型划分为六节点曲边三角形网格,获得单元和节点信息后,采用数值积分对目标强度进行计算。曲边三角形网格的最大边长hmax[18]应满足:

(18)

式中:c0为声速;fmax为最大计算频率。

算例中的水下目标表面为刚性,声速c0=1 500 m/s,入射波为平面波,无特别强调时声源与目标几何中心的距离为10 000 m。

3.1 刚性球的散射

为了验证曲面三角形单元数值积分方法的准确性,考虑半径a=1 m的刚性球散射。计算频段为50～8 000 Hz,步长50 Hz,数据点个数m=160,由式(18)可知,网格尺寸需满足hmax≤62.5 mm。

由于刚性球形状规则,可借助球Bessel函数jn和球Hankel函数hn,采用分离变量法获得目标强度的Rayleigh简正级数解,对式(3)中的Kirchhoff近似积分I直接求解,可得近似解析解。Rayleigh简正级数解和Kirchhoff近似解析解分别为

(19)

(20)

取均方根误差(L2范数):

(21)

首先将刚性球表面划分为若干个六节点曲面三角形单元,对比不同积分方式所得的数值结果。网格尺寸hmax取60 mm与30 mm时,三角形区域上7积分点得到的L2范数为0.264、0.067,正方形区域上3×3积分点得到的L2范数为0.268、0.067。两种积分方式所得结果相近,与正方形区域相比三角形区域的积分点数量更少,因此三角形区域7点高斯积分将用于接下来的数值算例及分析。图3给出了目标强度TS随频率的变化曲线,可以看出,曲面三角形(hmax=60 mm)数值积分与Kirchhoff近似解析解吻合良好。与简正级数解相比,在低频区域(Rayleigh区)差距较大;当f>2 000 Hz时,三者之间的数值差距在1 dB以内,但Kirchhoff近似解与简正级数解的起伏周期不一致。

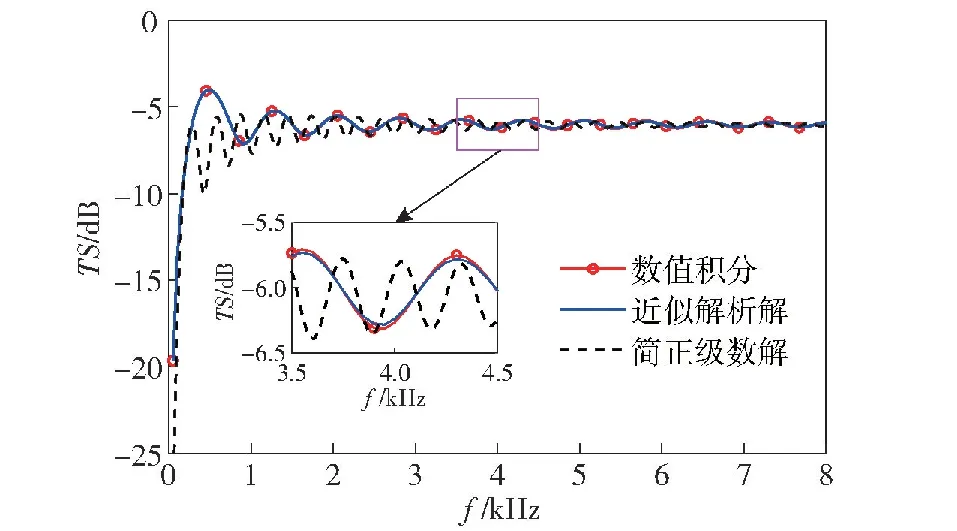
图3 球的目标强度

为验证六节点曲面三角形数值积分方法的计算效率,将其与基于三节点平面三角形单元的板块元方法对比,根据声学网格经验,平面三角形网格的尺寸不大于c0/(6fmax),即31.25 mm。提取曲面三角形单元的单元和顶点坐标等信息,生成平面三角形单元,此时二者的网格尺寸与网格数量相同,节点数量不同。然后分别采用数值积分法和板块元方法计算刚性球的目标强度,表1给出了不同网格数量下两种方法的计算时长。采用的处理器为Intel(R) Core(TM) i7-9750H,内存8 GB;MATLAB软件版本为R2019b,为提高程序的执行效率,采用向量化的数组运算代替循环单元。

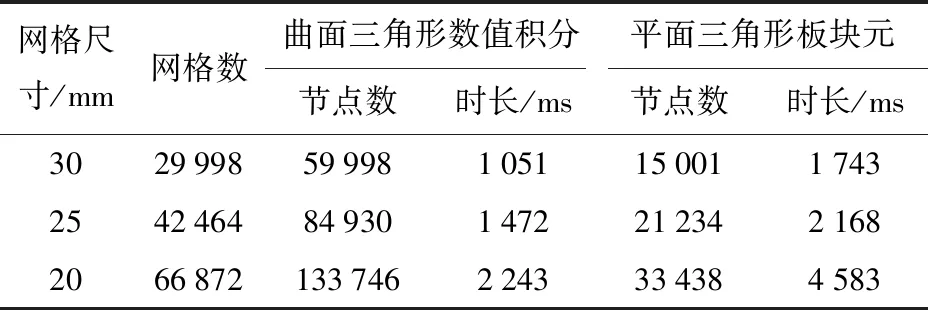
表1 计算球目标强度所需的网格及时长

由表1可知,当网格数量相同时,数值积分的计算速率大于板块元方法。对于每个网格,数值积分中曲面三角形的积分点个数为7,大于板块元中平面三角形的顶点个数3,但数值积分方法的时长较短,原因是板块元方法需将全局坐标系下的顶点坐标变换到局部坐标系,涉及到庞大的矩阵运算,耗费时间较长。

图4给出了不同网格尺寸下两种方法的L2范数,为便于对比,hmax为30～60 mm时,板块元的计算结果也于图中给出。由图4可知,目标强度的L2范数随着网格细化而减小,当网格尺寸hmax≥25 mm时,曲面三角形数值积分方法,所得结果的误差小于板块元方法,具有较高的精度。原因在于与平面三角形相比,在网络数量较少时,曲面三角形可以更好地拟合球面的形状。虽然可以通过增加平面三角形的单元数量更准确地拟合曲面形状,但划分的网格数量很大。当网格尺寸hmax≤20 mm时,两种算法得到的L2范数相近。

3.2 有限长椭圆柱的散射

考虑有限长刚性椭圆柱声散射,取椭圆柱的中心为坐标原点,入射方向与z轴方向垂直,声线处在Oxy平面内,如图5所示,声波照射亮区不包括端面,仅为侧面。椭圆柱的尺寸参数为长半轴a=2.5 m,短半轴b=1 m,高度h=4 m。

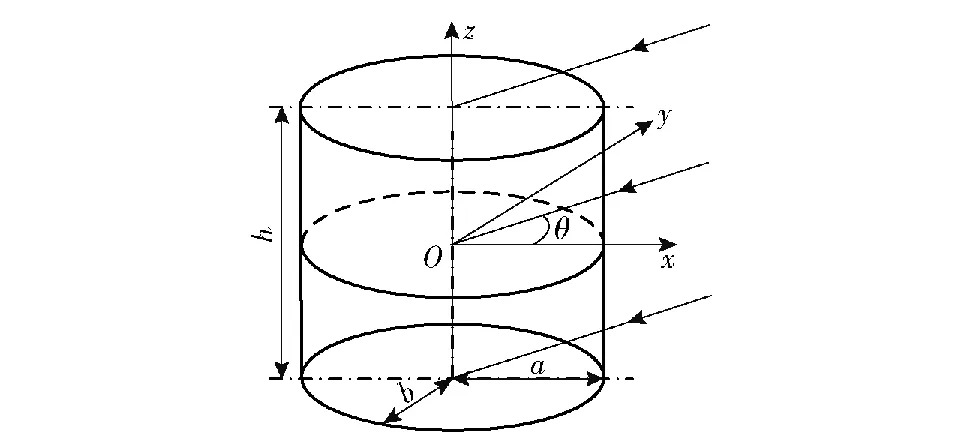
图5 有限长椭圆柱声散射

采用稳相法积分导出的亮点模型[21]描述椭圆柱面的回波,可得

(22)

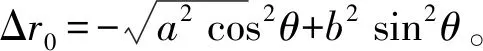
取入射角θ=45°,计算频段2 000～10 000 Hz,步长50 Hz,数据点个数161,采用曲面三角形数值积分和平面三角形板块元对其目标强度进行计算。表2给出了不同网格数量下的计算时长,可以看出,当网格数量相同时,数值积分方法的计算速率大于板块元方法。

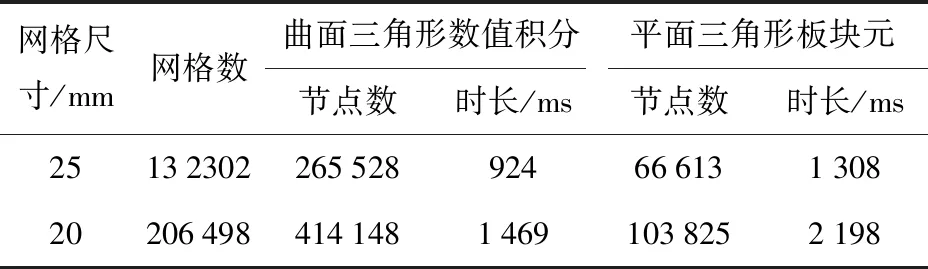
表2 计算椭圆柱目标强度所需的节点数量及时长

图6给出了不用频率下的目标强度曲线,计算时采用的网格尺寸为25 mm。然后计算频率f=5 000 Hz、入射角θ为0°～180°时椭圆柱的目标强度,步长2°,得到的结果如图7所示。由图6与图7可知,板块元、数值积分和亮点模型3种计算方法的计算结果吻合良好。

图6 不同频率下椭圆柱的目标强度

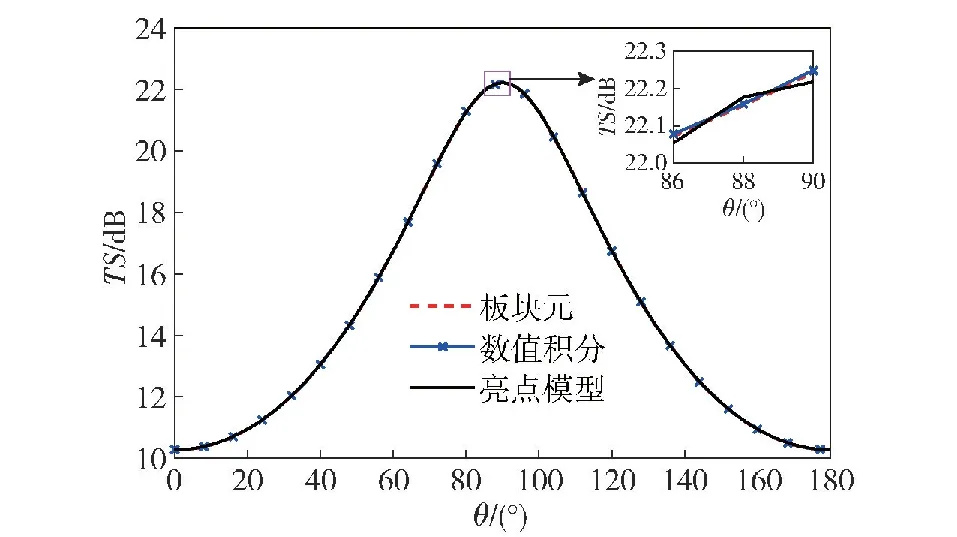
图7 不同入射角下椭圆柱的目标强度

3.3 球冠圆柱的散射

图8为刚性球冠圆柱的散射特性,该模型由半球形冠部和有限长圆柱构成。几何尺寸为球和圆柱的半径r=0.25 m,圆柱高度h=1.75 m,坐标原点位于圆柱中心。θ=0°时声波从半球面入射,θ=90°时声波从正横方向入射。

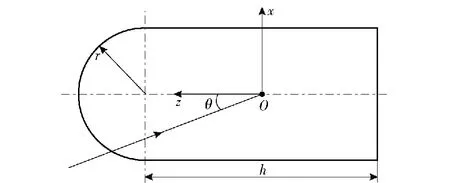
图8 球冠圆柱声散射

最大计算频率为10 000 Hz时,网格尺寸需满足hmax≤50 mm,取网格尺寸为50 mm,对应的网格数量为2 930,节点数量为5 926。图9给出了θ=90°时球冠圆柱的目标强度,本文结果与有限元-完美匹配层法[2]得到的结果在高频区域吻合良好,当f>2 000 Hz时,二者之间差距在1 dB左右;在中低频较不准确,原因是本文方法基于Kirchhoff高频近似,在低频部分存在误差。

图9 正横方向入射时球冠圆柱的目标强度

图10给出了不同入射角度下球冠柱的目标强度,步长为1°。当θ=0°,只有半球面的声散射,由式(20)可得入射波频率为6 000 Hz、8 000 Hz时球冠圆柱的目标强度分别为-18.06 dB、-17.59 dB。当θ=180°,只有圆端面的声散射,其目标强度为

图10 不同入射角下球冠圆柱的目标强度

(23)

由此可得,频率为6 000 Hz、8 000 Hz的平面波入射时,球冠圆柱的目标强度分别为-2.10 dB、0.40 dB,与当前计算结果吻合。

此外,由图10可知,由于不同入射角度下,球冠圆柱的声散射主导区域不同,目标强度随入射角的变化较为复杂,大致可分为3个部分,主导区域分别为半球面、圆柱面和圆端面。正横方向入射时球冠圆柱的目标强度最大,原因是正横方向入射时,回波成分主要由圆柱面的镜反射回波构成,散射的面积较大,所以目标的回波很强。

3.4 Benchmark潜艇的散射

最后研究Benchmark潜艇[22]的声散射特性,按比例缩小的潜艇模型如图11所示,缩小比例为 1∶15。 数值计算时,频率取15 000 Hz与20 000 Hz,入射角θ为0°～360°,步长取1°,θ=0°时声波从艏部入射,θ=180°时声波从艉部入射。为满足计算要求,曲面三角形网格尺寸取25 mm,共划分单元 22 874个,节点45 750个;平面三角形网格尺寸取12.5 mm,共划分单元91 412个,节点45 708个。

图11 按比例缩小的Benchmark潜艇模型

为进一步验证数值仿真结果的准确性,开展了湖上测试实验,实验模型的材料为不锈钢,厚度 3 mm。 水听器布置在模型与换能器之间,三者中心的布放深度均为10 m,模型距离水听器6.55 m,换能器距离水听器7.95 m,实验布置图如图12所示。测试过程中保持换能器的位置固定,水平匀速旋转处于悬挂状态的缩比潜艇模型,以获得全方位声散射信号。

图12 试验设备布置图

图13给出了Benchmark潜艇缩比模型回声强度ES的空间分布特性,由图可知,数值积分结果与实验测试结果的变化趋势基本吻合,说明了本文方法的可靠性。当声波从艉部及其附近入射时,实测值大于仿真值,原因是实验模型包含仿真模型不具有的螺旋桨,螺旋桨对目标的回波具有贡献。此外,在其他入射角度下,实测值与仿真值也存在一些偏差,一方面由于在实际测量过程中模型可能会有一定程度的倾斜,很难保证完全水平或标准正横向入射;另一方面试件在加工及焊接过程中难以避免地会产生几何尺寸及形状误差,从而影响实验模型的目标强度。

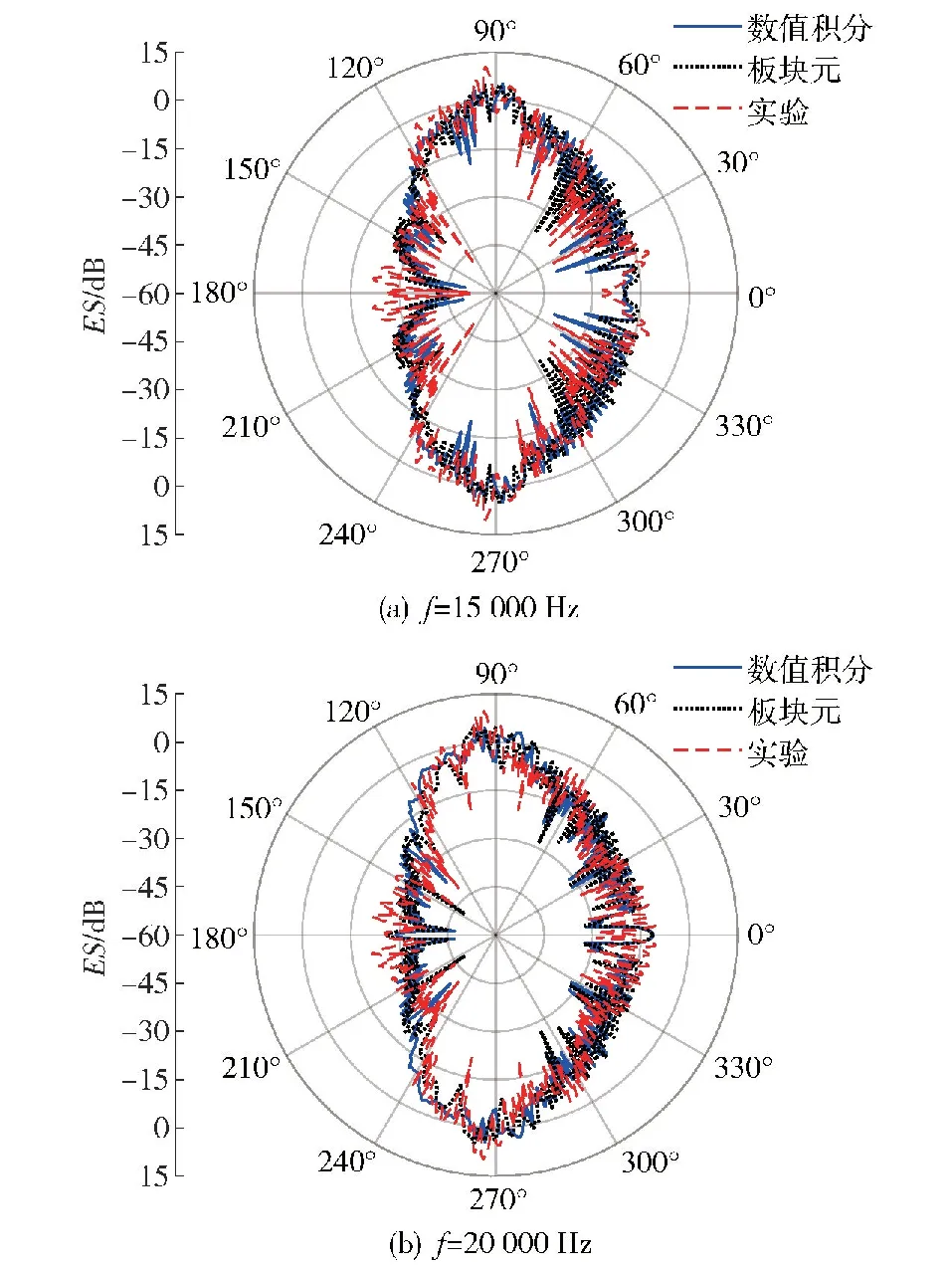
图13 Benchmark缩比模型的回声强度

4 结论

本文基于Kirchhoff近似和曲面三角形单元建立了水下目标收发合置目标强度计算模型,采用六节点曲面三角形单元离散目标表面,并对亮区内曲面单元的散射声场求和,得到目标的总散射声场。对4种典型目标的声散射计算结果表明:

1)与平面三角形相比,曲面三角形可以更好地拟合曲率较大目标的几何形状,所需的网格数量更少。

2)由于采用了Kirchhoff近似,本文方法更适用于高频段内水下目标的散射特性分析。

3)通过湖上测试得到了Benchmark潜艇缩比模型目标强度的空间分布特性,测试结果与仿真结果吻合较好。

4)基于曲面三角形单元的高斯-勒让德数值积分方法在高频具有良好的求解精度,具有一定的工程实用价值。