快速求解数值积分的花朵授粉算法

周慧 曾箫潇

摘  要： 针对当前数值积分精度不高、速度慢等问题，提出一种快速求解数值积分的花朵授粉算法，本算法对花朵授粉算法的局部搜索迭代公式和数值积分公式进行重新定义。通过10个函数积分仿真实验，结果表明本文设计的算法在迭代次数较少的情况下求解普通函数、奇异函数和振荡函数积分，且与其他智能算法相比，本算法具有一定的优势。

关键词： 花朵授粉算法; 数值积分;函数

中图分类号： TP391.4    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2020.07.030

本文著录格式：周慧，曾箫潇. 快速求解数值积分的花朵授粉算法[J]. 软件，2020，41（07）：148-151

A Fast Flower Pollination Algorithm for Solving Numerical Integration Problem

ZHOU Hui¹， ZENG Xiao-xiao^2*

（1. Guangxi University of Science and Technology， Liuzhou 545006， Guangxi， China;2. Guangxi Science & Technology Normal University， Laibin 546199， Guangxi， China）

【Abstract】： Aiming at the problems of low accuracy and slow speed of current numerical integration， This paper presents a flower pollination algorithm for solving numerical integrals quickly， this algorithm redefines the local search iterative formula of flower pollination algorithm and numerical integral formula. Through 10 function integral simulation experiments， the results show that the algorithm designed in this paper can solve ordinary function， singular function and oscillation function integrals with fewer iterations， compared with other intelligent algorithms， this algorithm has certain advantages.

【Key words】： Flower pollination algorithm; Numerical integration; Function

0  引言

在數学分析中，利用牛顿-莱布尼兹公式计算定积分并不总是可行的，因为有些函数的原函数无法用初等函数表示，甚至无法有解析表达式，因此只能采用数值积分方法。数值积分的传统方法有矩形公式、梯形公式、辛普森公式和牛顿-柯特斯求积公式等^[1]，其使用也具有一定的局限性。近年来涌现一些智能算法对其进行求解，如文献[2]提出粒子群算法数值积分方法研究，文献[3]将Chebyshev小波算法设计求解数值积分，文献[4]提出差分进化算法求解数值积分问题，文献[5]提出基于蛙跳算法求解任意函数的数值积分，文献[6]提出改进的蝙蝠算法在数值积分中的应用研究，文献[7]提出数值积分的

回溯搜索优化算法，文献[8]提出基于幂函数变步长神经网络求解数值积分方法，文献[9]提出基于生物地理优化算法的数值积分方法实验，文献[10]提出基于细菌觅食算法求解数值积分，文献[11]提出求数值积分的一种新算法，文献[12]提出求解数值积分问题的快速混合算法及其他方法[13-15]等。虽然上述方法在一定程度上提高了解的精度，但解的精度和求解速度还有待于提高。针对此问题，本文提出一种快速求解数值积分的花朵授粉算法。

1  花朵授粉算法

1.1  基本花朵授粉算法

Yang模仿了开花植物中花朵授粉过程的生物学特点发展了花朵授粉算法（Flower Pollination Algorithm （FPA））^[16]，其基于以下主要规则^[17]：

（1）全球授粉过程通过生物和异花授粉发生，传粉者的运动具有Levy飞行的形式。

（2）局部授粉过程被认为是非生物和自花授粉过程。

（3）传粉者提供花的稳定性，其与授粉过程中所涉及两种花相似性的繁殖概率成正比。

（4）通过转换概率控制全部授粉与局部授粉，转换概率对局部授粉轻微倾斜。

基于上述规则，花朵授粉算法的迭代公式：

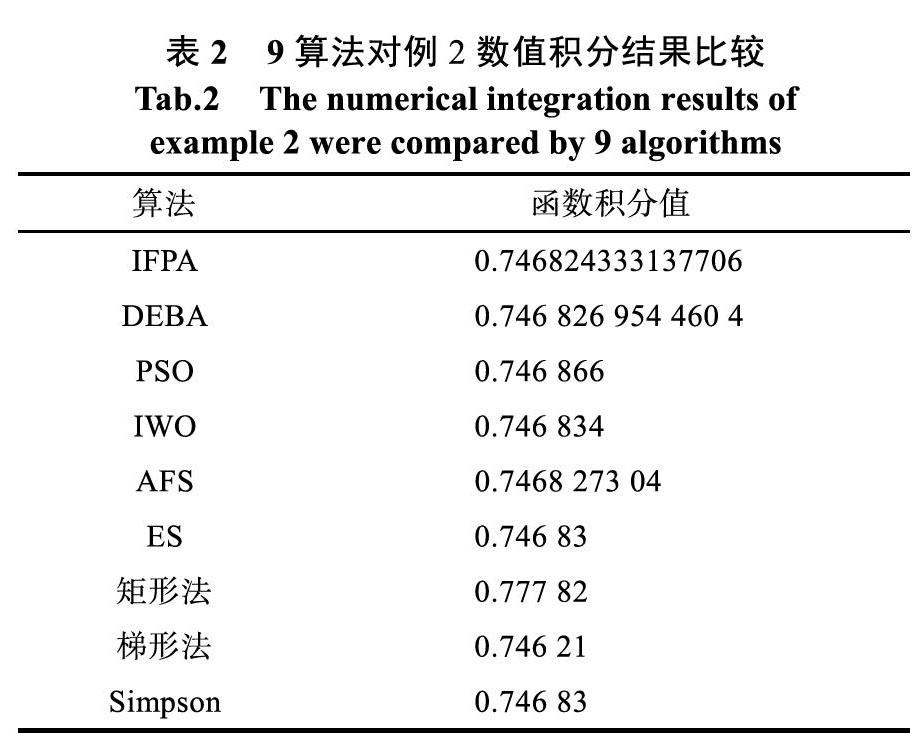
[6]、[20]和[22]比较结果如表4所示。从表4可知，IFPA算法求解结果次于DEBA和PSO算法，优于IWO和神经网络算法。

例5 积分函数

该积分函数的精确值为-0.0073279，实验参数设置与文献[6]相同，本文算法计算的数值积分与文献[2]、[6]、[19]和[20]比较结果如表5所示。从表5可知，IFPA算法求解结果均优于其他算法。例5函数适应度变化曲线图如图2所示。

综上所述，本文共对10个函数进行仿真实验，其中有普通函数、奇异函数和振荡函数，从实验比较结果可知，除了例3比其他智能算法精度较差以外，对其他函数，本文算法求解结果精度较高且迭代次数更少，基本上在20次以内获得较优解，因此本文算法在求解数值积分方面具有一定的优势。

4  结束语

本文提出了一种快速求解数值积分的花朵授粉算法，重新定义了花朵授粉算法的局部迭代公式和求积公式，对10个不同积分函数进行测试，仿真结果验证了该方法的有效性和可行性，与其他智能算法相比，该算法在精度和迭代次数方面具有一定的优势，不仅能计算普通函数的积分问题，而且能计算奇异积分和振荡积分。

参考文献

1. 李庆扬， 王能超. 数值分析[M]. 北京： 清华大学出版社， 2008.

2. 韦杏琼， 周永权. 基于粒子群算法数值积分方法研究. 微电子学与计算机， 2009， 26（7）： 117-119.

3. 刘智政， 吴金良， 杨宙. 数值积分公式的Chebyshev小波算法设计及应用. 江西科学， 2018， 36（6）： 954-960.

4. 邓泽喜， 黄飞丹， 刘晓冀. 一种求解数值积分的差分进化算法. 计算机工程. 2011， 37（20）： 206-210.

5. 赖志柱， 基于蛙跳算法求解任意函数的数值积分. 六盘水师范学院学报， 2013， 25（2）： 77-80.

6. 肖辉辉， 段艳明. 改进的蝙蝠算法在数值积分中的应用研究. 智能系统学报， 2014， 9（3）： 364-371.

7. 王海龙， 苏清华， 胡中波. 数值积分的回溯搜索优化算法. 湖北工程学院学报， 2017， 37（3）： 38-42.

8. 李哲， 王冬冬. 基于幂函数变步长神经网络求解数值积分方法. 计算机应用与软件， 2011， 28（9）： 123-125.

9. 张晶， 唐权华， 贾璐. 基于生物地理优化算法的数值积分方法实验. 实验室研究与探索， 2014， 33（12）： 20-22.

10. 郭德龍， 周锦程. 基于细菌觅食算法求解数值积分. 科技视界， 2018， 13（2）： 12-14.

11. 郭德龙， 罗琼， 罗泽龙. 求数值积分的一种新算法. 黔南民族师范学院学报， 2014， 34（2）： 95-97.

12. 刘英华， 董晶. 一种求解数值积分问题的快速混合算法[J]. 宁德师范学院学报， 2016， 28（1）： 19-23.

13. Wanxin He， Yan Zeng， Gang Li. A novel structural reliability analysis method via improved maximum entropy method based on nonlinear mapping and sparse grid numerical integration， Mechanical Systems and Signal Processing. 133（2019）： 106247-106268.

14. Emanuele Grossi， Ahmed A.Shabana. Analysis of high-   frequency ANCF modes_Navier–Stokes physical damping and implicit numerical integration.Acta Mech 230， 2581- 2605（2019）.

15. Felix Scholz， Bert Juttler. Numerical integration on trimmed three-dimensional domains with implicitly defined trimming surfaces. Computer methods in applied mechanics and engi?neering. 357（2019）： 112577-112599.

16. Yang， X. S（2012）， Flower Pollination algorithm for global optimization， in： Unconventional Computation and Natural Computation， Lecture Notes in Computer Science， Vol. 7445， pp.240-249.

17. 肖辉辉， 万常选， 段艳明. 一种改进的新型元启发式花朵授粉算法[J]. 计算机应用研究， 2016， 33（1）： 126-131.

18. 周永权， 张明， 赵斌. 基于进化策略方法求解任意函数的数值积分， 计算机学报， 2008， 31（2）： 196-205.

19. 聂黎明， 周永权. 基于人工鱼群算法求解任意函数的数值积分， 数学的实践与认识， 2009， 39（19）： 127-134.

20. 陈欢， 周永权. 杂草优化算法的改进分析与应用研究[D]， 广西民族大学， 2013， 33-39.

21. WANG X H， HEY G， ZENG Z Z. Numerical integration study based on triangle basis neural network algorithm[J]， Journal of Electronics & information Technology， 2004， 26（3）： 294-299.

22. 韦修喜， 周永权， 蓝晓玲. 一种基于泛函网络求数值积分方法研究[J]， 计算机科学. 2009， 36（4）： 224-226.

23. BURDEN R L， FSIRES J D. Numerical analysis[M]， Toronto：ThomsonBrooks/cole， 2001：206-212.