弹箭角运动的非线性吸引域估计
2023-09-07李东阳常思江王中原
李东阳, 常思江, 王中原
(南京理工大学 能源与动力工程学院, 江苏 南京 210094)
0 引言
对于飞行中的弹箭,在攻角δ较小的情况下,可将作用在弹箭上的气动力和力矩视为攻角的线性函数,并可采用sinδ≈δ、cosδ≈1的线性化假设,据此形成线性化外弹道理论,该理论曾在很大范围内成功地预示了弹箭运动,促进了弹箭飞行性能设计的发展。然而,弹箭在各种条件下的实际运动,总是具有不同程度的非线性[1]。随着弹箭外形及其飞行条件的日益复杂化、多样化,弹箭运动的非线性特征也愈发凸显。如在大攻角情况下,作用于弹箭的气动力和力矩一般为攻角δ的非线性函数,有的还是弹箭滚转方位角的非线性函数(如诱导侧向力矩),因而数学上无法利用线性理论开展研究;对于一些客观存在的现象,如“行进军舰上发射某尾翼式低速旋转火箭,左舷发射稳定、右舷发射不稳定”、“某些火箭弹飞行中出现锥形运动而致失稳”等,线性理论也无法给出合理的解释。因此,弹箭非线性运动理论应运而生并迅速发展。
20世纪60年代至本世纪初,一些学者就强非线性静力矩[2]、非对称再入飞行器的非线性运动[3-4]、转速-攻角闭锁与灾变性偏航[5-6]、弹箭非线性动力学[7-8]、有控弹非线性稳定性[9]等问题,利用非线性数学工具开展研究,建立了弹箭非线性运动研究的理论方法体系,取得了大量研究成果;Mc Coy等[10]通过开展靶道飞行试验及气动系数辨识,获得了大量的弹丸非线性气动力数据。近20年来,随着弹箭技术的进一步发展,弹箭非线性运动研究继续受到广泛关注。Morote 等就无控火箭共振闭锁[11]、尾翼弹灾变性偏航控制[12-13]、尾翼弹非线性滚转运动[14]、高阶非线性气动力[15]等开展了一系列深入研究;韩子鹏等[16]对弹箭非线性运动的国内外研究成果进行了系统梳理,主要涉及非旋转尾翼弹平面非线性运动、旋转弹箭非线性运动、非线性气动系数获取等方面;李臣明等[17]对远程弹箭的转速闭锁现象进行了理论;Li等[18]、Chang等[19]和李东阳等[20]重点研究了弹箭非线性运动方程的解析解,其中文献[18]在Murphy 等[21]关于转速-攻角闭锁解析模型的基础上,进一步完善了攻角-转速闭锁的解析解,文献[19-20]则分别探讨了利用同伦分析法、正规形法求取高精度攻角解析解的可行性,并据此开展了弹箭稳定性分析、参数设计等相关应用;此外,Cross等[22]利用数值仿真对制导炮弹的非线性稳定性开展了分析;钟扬威等[23]、杨杰等[24]利用分岔理论对弹箭非线性角运动等开展了研究。可以预见,弹箭非线性运动理论将是从根本上提高弹箭性能设计水平的重要基础和有力工具。
弹箭非线性运动的稳定性不仅与系统参数(如气动参数、结构参数等)有关,而且与初始条件密切相关,这是非线性系统与线性系统的不同之处。故要使弹箭达到期望的稳定状态,必须对其初始条件加以限定。定义一个包含初始条件的紧集,若从该集合内任一点出发的轨迹不超出该集合且最终都将收敛到系统的某一个平衡点,则称该紧集为对应稳定平衡点的吸引域[25-26]。因此,只有当初始运动状态在吸引域内时,弹箭运动才是稳定的,这就使得吸引域的确定变得十分重要。在开展弹箭稳定性设计时,必须通过设计相关参数,确保吸引域包含弹箭的可能运动状态范围。然而,一般来说,除一些特殊的系统外,非线性系统准确的吸引域确定相当困难[27],一般通过解析或数值计算方法进行估计。现有的吸引域估计方法,主要采用李雅普诺夫理论进行问题的描述[28]。对于多项式系统,在吸引域问题的求解上普遍采用多项式的平方和方法[25]。该方法的本质是将多项式的正定要求松弛为平方和问题,进而利用平方和规划方法求解[29]。平方和规划包含了多项式半正定问题的求解、平方和优化问题与平方和可行性问题的求解,以上问题在具体的吸引域估计问题中都会遇到[26]。尽管该方法具有一定的保守性,且其计算复杂度随着系统的维数和所寻求的李雅普诺夫函数阶次的增大而迅速增大,以及仅适用于多项式系统的局限性,但它使得吸引域的估计变得可行,与基于蒙特卡洛轨迹积分的方法相比,平方和规划方法给出的结果具有可靠性和绝对性[30],并给出了吸引域的解析表达式,这是该方法的优势所在。
因此,本文拟探讨平方和方法在弹箭角运动非线性吸引域估计中的应用。对此,将针对两种情形开展吸引域估计:一是无控尾翼弹平面非线性运动,考虑高阶非线性静力矩以及二次方非线性阻尼;二是脉冲末段修正迫弹[31]的空间非线性运动,考虑非线性法向力系数、马格努斯力矩系数、俯仰力矩系数及赤道阻尼力矩系数等。由于平方和规划仅适用于多项式系统,故在角运动方程的建模中需要对几何非线性等非多项式因素进行多项式近似。本文研究旨在为弹箭非线性运动研究提供新的有效理论工具。
1 基于平方和规划的吸引域估计方法
本节将简要介绍基于平方和规划的非线性吸引域估计方法。对于一个非线性自治多项式:

(1)
式中:x为状态变量,x∈n;t为自变量;f(x)是n×1维的多项式向量场;x0为t=0时的状态值,即初始条件。不失一般性,设原点是系统的平衡点,于是f(0)=0,且原点渐近稳定,则根据直接李雅普诺夫定理(定理1),原点的吸引域可定义为
{x0∈n: 若x(0)=x0则
(2)
定理1[25-26]若存在连续可微标量函数V(x):n→和标量γ∈+,使得
V(x)>0, ∀x≠0∧V(0)=0
(3)
Ω:={x:V(x)≤γ}
(4)
Ω⊆{x:(∂V(x)/∂x)f(x)<0}∪{0}
(5)
则原点渐近稳定,Ω是原点的确切吸引域式(2)的子集,可作为吸引域的一个估计,γ为其水平集。
可见,所寻找吸引域的估计,需满足式(3)~式(5)对V(x)和γ的约束。而式(3)~式(5)中,既含有不等式约束,又含有集合包含约束。利用代数几何学,集合包含关系可以通过著名的推广S-procedure(定理 2)[32]转化为不等式约束。
定理2(推广S-procedure)给出多项式g0(x),…,gm(x)∈R[x]和多项式s1(x),…,sm(x)∈Σn,R[x]代表系数为实数的多项式集合,Σn代表n个变量组成的平方和多项式集合,若
(6)
则
{x|g1(x),…,gm(x)≥0}⊆{x|g0(x)≥0}
(7)
因此,问题转化为处理一系列多项式不等式。通常一个多元多项式的非负性是很难确定的,属于非确定性多项式(NP)困难问题,解决的思路是利用平方和松弛方法[25],将多项式的非负性问题转化为平方和问题,进而利用平方和规划方法[25-26]对问题进行求解。例如,验证一个多项式s(x)∈R(x)是否为正,就等价于验证是否存在正定矩阵Q,使得
s(x)=ZT(x)QZ(x)∈Σn
(8)
式中:Z(x)为单项式向量。关于平方和方法的具体内容,可参见文献[26,32]。
综上所述,吸引域估计问题可以转化为以下平方和问题:
(9)
式中:l1(x)∈R(x)且l1(x)>0,一般取εxTx,ε为大于0的常数(如取为10-6);s1(x)辅助算子,为一定阶数的平方和多项式。
为了进一步优化吸引域的估计,可通过一个称为形状函数的多项式h(x)>0[26, 33],将原问题式(9)改写为一个双线性平方和规划问题:
(10)
式中:φ为形状函数h(x)的水平集,φ∈;l2与l1类似,同为多项式小量;s2与s1类似,亦为平方和辅助算子。
将上述双线性问题解耦为两个单线性优化问题[26],采用迭代算法(常称为V-s迭代算法[26-27, 33])进行求解,给定一个已知且可行的初始李雅普诺夫函数V0和形状函数h,并令V(x)=V0,具体步骤简述如下:
1)固定V(x),利用二分法求得γ的最大值γ*,并记下此时的s2,即

2)固定V(x)、变换γ*,利用二分法求得φ的最大值φ*,并记下此时的s1,即

3)固定s1、s2、φ*、γ*,求解新的满足以下约束的李雅普诺夫函数V(x),这里可根据需要通过待定系数设定V(x)的阶次(如2次、4次或6次李雅普诺夫函数):
-[(∂V(x)/∂x)f+l2]-(γ*-V(x))s2∈Σn
(γ*-V(x))-(φ*-h)s1∈Σn
V(x)-l1∈Σn
V(0)=0
4)V(x)=V(x)/γ*;
5)重复以上步骤,得到最终的李雅普诺夫函数V(x)=V(x)/γ*和相应的吸引域估计Ω:={x∈n:V(x)<1}。停止条件可为以下任意一种:
①遇到数值计算不可行问题;
②相邻两次φ的最优值小于既定容许度,如0.001;
③预定的迭代次数i。
值得注意的是,在寻找新的李雅普诺夫函数这一步(步骤3)中,s1、s2为已知且固定,与李雅普诺夫函数的阶次无直接关系。
2 考虑高阶气动力的无控弹箭角运动吸引域
引起弹箭非线性运动的因素包括气动力非线性、结构非线性及几何非线性等,其中又以气动力非线性占主导地位[1]。Morote等[12]的研究结果表明,对于某弹箭,当静力矩系数关于攻角的阶数达到7次时才能准确地拟合试验数据;Liano等[15]也发现,为准确预测转速闭锁,当攻角为12°和20°时,与滚转角相关的非线性力矩关于攻角的阶数分别不能低于 5次和7次。因此,对于弹箭非线性运动研究,有必要引入高阶气动力系数。将利用第1节中的方法,研究无控尾翼弹平面非线性角运动的吸引域估计。
2.1 无控尾翼弹非线性平面角运动方程
引入高阶气动力,考虑5次方和7次方非线性静力矩以及2次非线性阻尼对角运动的影响。无控尾翼弹的平面非线性角运动方程可描述为
δ″+(H0+H2δ2)δ′-(M0+M2δ2+M4δ4+M6δ6)δ=0
(11)

2.2 平衡点的稳定性
若该角运动方程的平衡点记为δ*,其满足:
(12)
因此,在高阶非线性静力矩系数的影响下,角运动可能存在除原点以外的其他平衡点。当不考虑阻尼项时,平衡点对应的特征根λ满足
λ2=M0+3M2δ*2+5M4δ*4+7M6δ*6
(13)
故原点对应的特征根满足λ2=M0<0,则平衡点为中心,稳定性无法由线性理论确定。以3次非线性静力矩为例,当M0、M2同号时,不存在其他平衡点,理论上不论初始条件如何,攻角都将做幅值为δ0的摆动;当M0、M2异号时,存在一对实平衡点δ*2=-M0/M2,且当M0<0时,δ*为不稳定鞍点。
当考虑阻尼项时,阻尼项的存在虽然不改变角运动方程式(11)的平衡点位置,但影响其稳定性,此时特征根满足
λ2+(H0+H2δ*2)λ-(M0+3M2δ*2+5M4δ*4+7M6δ*6)=0
(14)
为了确定攻角运动的稳定性,需综合考虑系统平衡点式(12)和阻尼项H0、H2的影响。原点的稳定性将由线性静力矩系数M0和线性阻尼系数H0共同确定,即当M0<0时,若H0<0,则原点为不稳定平衡点,若H0>0,则原点为稳定平衡点。此外,文献[20]表明,考虑阻尼时,符号相反的H0、H2使得非线性的角运动系统出现了极限环。极限环的稳定性与原点稳定性的共同作用决定了攻角幅值的变化规律,如表1所示。详细讨论参见文献[20]。

表1 系统稳定性分析
由表1可知,对于不同符号H0、H2的组合,可能存在稳定或不稳定的极限环。对于原点为稳定平衡点的系统,设计者感兴趣的是弹箭在什么初始条件下角运动可以收敛到原点。
2.3 吸引域估计结果
采用文献[19]中的平面角运动参数开展具体的吸引域估计,其中马赫数Ma=0.6,静力矩系数M0=-5.0×10-5,M2=-4.5×10-4,M4=-8.0×10-3,M6=0(由于缺乏数据,这里取为0值),阻尼力矩系数H0=2.0×10-3,H2=-0.4。如表1所示,对于该H0、H2的具体值,原点为稳定平衡点,且存在一个不稳定极限环,相轨线图如图1所示。

图1 不同初始条件下攻角运动相平面图
当角运动初始条件位于此极限环内时,攻角运动收敛到终点;角运动初始条件在此极限环外时,攻角运动发散。因此,稳定原点的确切吸引域由该极限环表示(见图1中的阴影区域),该极限环可通过数值计算并逆向积分得到。需要说明的是,并非任何系统都可以采用逆向数值积分方法获得其确切吸引域。如Van de Pol系统,由于其形成了不稳定极限环,从环内所有点出发的轨迹均收敛于环内平衡点,故该平衡点的吸引域就是该极限环包围的区域,进而可以通过逆向积分,使轨迹最终收敛于极限环,得到确切吸引域,而角运动方程式(11)所示系统,本质上恰为一Van de Pol系统。
取x1=δ、x2=δ′,则角运动方程式(11)可表示为
(15)
利用V-s迭代算法对原点的吸引域进行估计,选取初始李雅普诺夫函数
V0=xTPx
(16)
式(16)中的P由李雅普诺夫方程ATP+PA=-I计算得到,A=(∂f/∂x)|x=0,I为单位矩阵;形状函数取为h(x)=xTx;利用V-s迭代算法,分别寻找 2次、4次和6次李雅普诺夫函数对吸引域进行估计,最终得到的李雅普诺夫函数分别记为V2、V4、V6:
V2=0.031 708δ2+134.146 533δδ′+585 313 523.361 843δ′2
(17)
V4=1.341 471e-5δ4-0.090 763δ3δ′+453 519.717 597δ2δ′2+228 473 313 060.431 2δδ′3+2.277 762e16δ′4-3.917 141e-7δ3+0.085 829δ2δ′+776.309 701δδ′2+2 696 018 997.682 03δ′3+0.027 334δ2+481.738 113δδ′+481 989 806.810 080δ′2
(18)
V6=6.535 639e9δ6-0.002 437δ5δ′-20.835 500δ4δ′2+5.912 217e8δ3δ′3+4.210 891e14δ2δ′4+0.000 19δ4δ′+1.829 569e19δδ′5+2.396 202e24δ′6-3.296 192e-10δ5-32.114 797δ3δ′2+9.010 24e6δ2δ′3-4.976 216e11δδ′4-1.172 415 2e16δ′5+1.818 161e-5δ4-6.580 880δ3δ′-7.076 783e4δ2δ′2+1.654 866e11δδ′3-8.684 899e14δ′4+2.375 432e-8δ3-0.010 868δ2δ′+1 825.386 293δδ′2+37 720 324.123 641 36δ′3+0.014 637 006 762 577 65δ2+429.817 180 706 390 3δδ′+285 374 579.309 986 1δ′2
(19)
吸引域估计结果如图2所示。

图2 不同阶次李雅普诺夫函数估计下的吸引域
由图2可见,随着李雅普诺夫函数阶次的增加,吸引域的近似效果逐渐提升。6阶李雅普诺夫函数的结果已无限接近确切吸引域。这一结果正如文献[34]所得结论,李雅普诺夫函数的阶次越高,可以越准确地接近确切吸引域。主要原因在于,当李雅普诺夫函数的阶次越高,可表达成的形状也越为多样,故高阶李雅普诺夫函数有能力表示形状复杂的吸引域。因此,基于平方和规划的非线性吸引域估计方法可用于分析弹箭角运动的稳定性,能够定量地确定角运动的初始稳定范围。
3 脉冲末修迫弹的非线性角运动吸引域
随着弹箭技术的发展,弹箭非线性运动研究已不局限于无控弹箭,对于有控弹箭的非线性分析也已开展过相关研究[9, 22],但限于研究工具的缺乏,这些工作尚不深入。将以脉冲控制的末修迫弹[31]为对象,开展非线性吸引域估计,根据所得吸引域反求脉冲参数设计应满足的约束,据此提出脉冲控制参数的设计方法。
3.1 非线性角运动方程及其多项式近似
为便于描述,定义弹轴坐标系(简称弹轴系),其原点O位于弹质心,x轴沿弹轴指向弹体头部为正,y轴沿水平方向,z轴在铅锤面内垂直于y轴指向下为正。在弹轴系内,弹体的速度和角速度分别表示为U=[uvw]T和ω=[pqr]T,u、v、w分别为弹体速度在弹轴坐标系三轴上的分量,p、q、r分别为弹体角速度在弹轴坐标系三轴上的分量;弹轴系相对于惯性坐标系的角速度在弹轴系内的投影可表示为Ωx=[pxqr]T,px表示该角速度的轴向分量。作用在弹体的横向(即沿y轴和z轴)气动力和气动力矩可以表示为如下复数形式:
(20)

弹体的横向运动在弹轴系下可表示为
(21)


(22)
不考虑马格努斯力,气动力和气动力矩系数可表示为
Cy+iCz=-CNαξ
(23)
(24)
其中:CNα为法向力系数;CMpα为马格努斯力矩系数;CMα为俯仰力矩系数。
考虑气动力非线性,则有
(25)
式中:CNα0、CNα2分别为线性和三次方法向力系数;CMpα0、CMpα2分别为线性和三次方马格努斯力矩系数。
将式(23)和式(24)代入横向运动方程组式(21),且弹轴系下角速度px≈0,并将自变量从时间t换为无量纲弧长s。为方便起见,选择变量
(26)
则角运动方程可写为
(27)
(28)
式中:η为几何非线性项,η=u/U。
由几何关系可知
(29)
则有
(30)
由气动力和重力沿速度方向的分量可得速度方程
(31)
其中:CD为阻力系数。
由于平方和计算工具(如SOSTOOLs、SOSOPTs、SeDuMi等[26-27, 33])只能应用于多项式,故式(27)需表示为多项式的形式,即对几何非线性η进行多项式近似。
为此,将式(29)和式(30)泰勒展开并取1次近似,可得
(32)
式中:O(·)为高阶小量表示符号。
为验证上述多项式近似系统代替原系统进行角运动稳定性分析的准确性,首先要分析二者的平衡点和平衡点稳定性是否一致,然后通过数值计算对比二者所得轨迹的一致性。
3.2 脉冲未作用时的吸引域估计结果
以文献[10]中提供的某120 mm迫弹作为无控弹平台,结构参数如表2所示。

表2 某120 mm迫弹结构参数[10]
由于末修迫弹是在弹道末段(如距离目标800~1 000 m)进行修正控制,其大部分弹道为无控弹道,末段启控点参数可作为末段运动的初始条件。假设弹体不滚转(P=0),以初速318 m/s、射角45°对上述120 mm迫弹进行无控弹道计算,其至目标斜距800 m处的弹道参数如表3所示,对应的角运动方程参数如表4所示。

表3 弹道末段起始位置的弹道参数

表4 弹道末段起始位置的角运动方程参数
此时,角运动方程式(27)具有唯一平衡点x*=[0.000 2 rad 0 0 0]T。在该平衡点进行线性化,线性化系统特征方程的两对特征根均具有负实部,则根据线性化理论,角运动在平衡点x*的邻域内可稳定收敛到x*。状态变量的数值积分结果如图3所示。

图3 原模型和多项式近似模型的相轨迹比较
如图3所示,多项式近似系统和原系统轨迹是一致的,验证了上述多项式近似系统代替原系统进行角运动稳定性分析的准确性。
对于弹箭的实际角运动而言,所允许的攻角和角速度是有范围的,故需要找到具有实际意义的攻角和角速度稳定范围,即开展吸引域估计。
假设在选定点附近一段时间内,弹箭速度、飞行高度、弹道倾角的变化忽略不计,则气动系数保持不变。将非线性气动力式(25)和几何非线性近似式(32)代入角运动方程式(27),并通过坐标转换将平衡点移至原点,之后可利用平方和规划估计其吸引域。
利用V-s迭代算法,分别寻找二次和四次李雅普诺夫函数,最终所得函数记为V2和V4:
V2=24.063 268α2+344.850 517αα′+24.063 267β2+344.850 514ββ′+279 665.08α′2+279 665.07β′2-0.009 189α-0.065 849α′
(33)
V4=0.291 549α4+8.517 460α3α′+0.583 178α2β2+8.467 055α2ββ′+1 204.838 384α2α′2+2 960.584 841α2β′2+8.466 879αβ2α′-3 496.704 7αβα′β′+4 404.953 287αα′3-0.000 430αα′2β′+4 305.759 8αα′β′2-0.000 508αβ′3+0.291 549β4+8.517 493β3β′+2 960.576 6β2α′2-1.018 918e-6β2α′β′+1 204.859 8β2β′2+0.000 402βα′3+4 309.150 272βα′2β′+0.000 544βα′β′2+4 404.883 9ββ′3+2 692 175.590 3α′4-8.036 145e-5α′3β′+5 401 623.866 9α′2β′2+0.000 749α′β′3+2 692 218.734 4β′4-0.000 242α3+0.018 099α2α′-0.000 243αβ2+0.028 630 1αββ′-0.074 852αα′2-6.852 724e-6αα′β′-2.955 652αβ′2-0.010 157β2α′
(34)
上述李雅普诺夫函数V2、V4等,必然满足V(x)>0。这是由于V(x)>0为多项式正定的条件,在平方和规划中已将其转化成平方和约束,即V(x)-l1(x)∈Σn(体现在V-s算法的第3步),故V(x)>0本身即为问题的约束条件,求得的V2、V4等自然满足该约束。计算所得吸引域分别为
(35)
其空间表达如图4所示,其在各相平面的轨迹(剖面图)如图5所示。
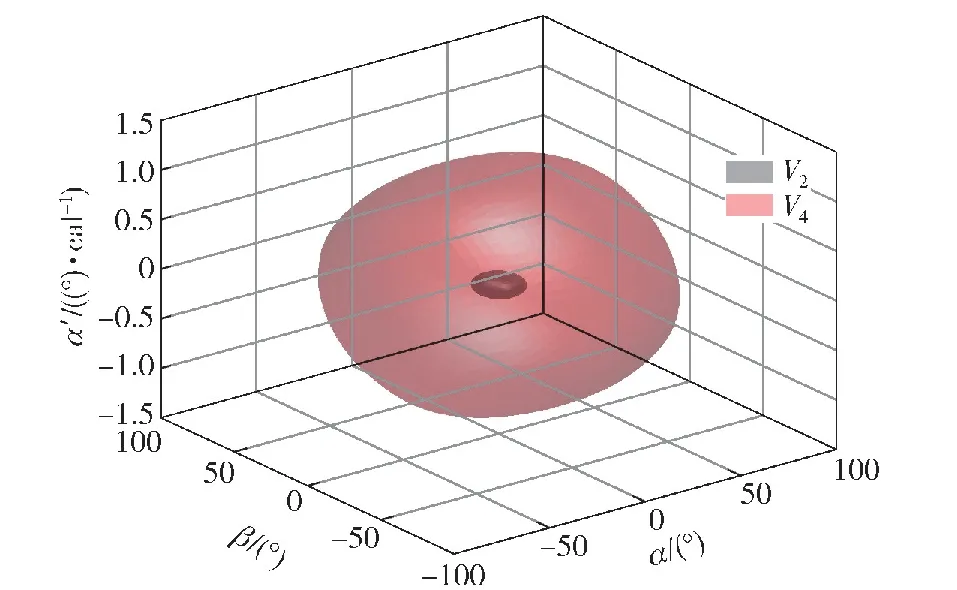
图4 吸引域估计结果的空间表示

图5 吸引域估计结果的剖面图
如图4和图5所示,基于平方和规划的吸引域估计给出了很好的结果。需要说明的是,上述计算是在假设弹箭飞行环境不变的条件下得到,因而只在相对较短的一段弹道上成立。上述计算结果表明,平方和规划方法用于确定角运动稳定范围是有效的。值得注意的是,由于式(26)表示的气动力仅考虑到立方次,如果能够建立更为准确的高阶气动力模型,将得到更加准确的结果。
3.3 脉冲作用下弹体稳定的初始条件范围
对于脉冲末修迫弹,发射后先做无控飞行,当飞入预定区域后(弹道末端,如距离目标800 m斜距处)启控,进行弹道修正以提高对目标的射击精度。由于采用的控制执行机构为脉冲发动机,在设计脉冲控制参数时,需要确定脉冲大小J、脉冲作用的轴向位置Lx(距质心,作用在质心前为正)以及脉冲作用的周向位置φJ(与弹轴系y轴的夹角,即脉冲方位角)。由于脉冲作用的时间极短(通常约几毫秒至几十毫秒),可认为其作用前后仅引起攻角和攻角速度的变化。
设脉冲作用前(记为t=0-)攻角状态为x0-=[α0,α′0,β0,β′0]T,脉冲作用后(记为t=0+)x0+=[α,α′,β,β′]T,则有
x0+=x0-+xJ
(36)
式中:xJ为脉冲作用引起的角运动状态增量,

(37)
若要保证脉冲作用前后的角运动稳定,需同时满足:
(38)
则稳定的角运动范围为上述两个集合的交集Ωx0-∩Ωx0+,设其仍具有吸引域所对应的李雅普诺夫函数之形式,则该交集可近似为
Ω∩={x0-|V((x0-+x0+)/2)<γ∩}
(39)
式中:γ∩为函数V((x0-+x0+)/2)的水平集。因此,可以方便地利用定理2处理集合包含关系,并利用平方和规划得到尽可能大的水平集γ∩。
考虑算例:脉冲冲量大小为J=60 N·s,作用轴向位置为Lx=0.083d(即质心前0.083d)。将上述脉冲参数值代入式(38),并利用平方和规划通过式(39)计算不同脉冲方位角φJ所对应的角运动稳定范围,即交集Ω∩的水平集γ∩。计算结果表明,对于不同的φJ,水平集γ∩的大小相同,但稳定区域Ω∩的位置随φJ的变化而变化,如图6所示。

图6 交集估计Ω∩在α′-β′平面上的位置变化
在图6所示α′-β′平面上,当φJ以45°为间隔从0~360°取值时,红色曲线为不同φJ所对应的Ωx0+,绿色曲线为稳定角运动初始条件的估计Ω∩,显然,Ωx0+的位置随着φJ的变化而变化,进而Ω∩也随着交集的变化而变化。
从图6还可看出,存在一定的区域,在任意脉冲方位角下,弹箭角运动均稳定。不妨将这样的区域记为Ω∀,且设其仍具有所对应的李雅普诺夫函数之形式,即
Ω∀={x0-|V(x0-)<γ∀}
(40)
则仍然可以通过集合包含问题优化计算得到水平集γ∀的尽可能最大值。
由于上述问题没有精确解,为验证平方和规划所得结果的正确性,下面引入另一种计算方法。由于二次李雅普诺夫函数给出的吸引域恰为椭球体,故γ∩和γ∀也可通过一定的几何关系得到。设二次李雅普诺夫函数给出的吸引域Ω2D的半径(即半长轴长)为rΩ,并定义
(41)
为脉冲增量xJ对应的半径,则易知脉冲作用下稳定角运动范围Ω∩的存在条件为
max (rJk/rΩk)<1,k=1,2,3,4
(42)
方便起见,下面将max (rJk/rΩk)简记为max (rJ/rΩ)。
对于二次李雅普诺夫函数,设椭球体Ω∩和Ω∀对应的半径分别为r∩和r∀,则根据几何关系,可得到半径与水平集之间的关系为
γ∩=max2(r∩/rΩ),γ∀=max2(r∀/rΩ)
(43)
各半径之间的关系为
(44)
r∀=2r∩-rΩ
(45)
同时可得到
(46)
且

(47)
上述关系意味着,可以通过优化计算得到γ∩后,直接由式(46)计算得到水平集γ∀;另一种方法是通过已知的rJ和rΩ直接计算γ∩和γ∀。
根据式(44)第1式可得,若r∩存在,也即脉冲在某个方位角φJ下作用时,存在稳定角运动范围的条件为
max (rJ/rΩ)<2
(48)
根据式(44)第2式可得,若r∀存在,即存在任意方位角下均能确保弹箭角运动稳定的初始条件,那么
max (rJ/rΩ)<1
(49)
对于本节算例中的二次李雅普诺夫函数V2,其半径为
(50)
当脉冲冲量为J=60 N·s、作用位置Lx=0.083d时,脉冲增量对应的半径为
(51)
利用平方和规划方法处理集合包含关系得到的γ∩,进而根据式(46)计算得到的γ∀如表5所示,同时给出了根据式(47)直接计算的γ∩、γ∀值。
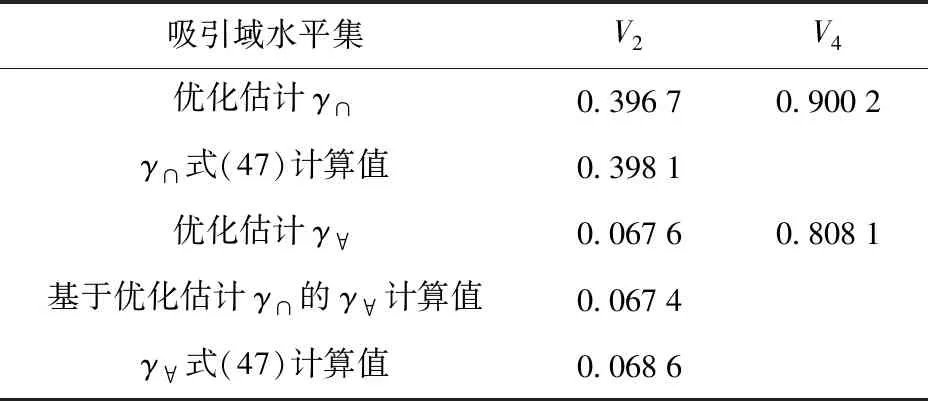
表5 吸引域半径计算结果
根据表5所示结果可见,优化计算所得估计结果与几何关系式(44)给出的结果非常接近,由此认为二者互相验证了各自的准确性。
在此基础上,对于已经过验证的平衡点吸引域Ω及其半径rΩ,若给定脉冲大小J和作用位置Lx,根据式(48)和式(49),即可判断此时是否存在稳定的角运动范围以及对任意脉冲方位角均稳定的角运动范围,并可根据式(47)计算出稳定角运动范围的水平集,进而由式(39)和式(40)确定出角运动稳定范围的具体位置。
3.4 应用:脉冲参数设计
上述结论可用于脉冲参数的设计,即根据吸引域估计结果反向确定出脉冲参数的设计范围,该范围内的任意脉冲作用均可使弹箭保持稳定的角运动。
将脉冲增量对应的吸引域半径表达式(41)代入式(47),可得
(52)
即
(53)
根据表5,有γ∀=0.068 6,代入式(53)即可得出满足水平集γ∀=0.068 6的脉冲参数J,Lx的所有可能组合(称为有效脉冲参数组合),如图7曲线与纵轴包围的区域所示,纵轴为脉冲作用在弹轴上的位置。

图7 满足水平集γ∀=0.068 6的脉冲参数组合
图7中曲线与纵轴包围的区域即为脉冲参数设计的有效范围。由此可见,对于一定的脉冲轴向作用位置,均对应一定的脉冲大小。这些脉冲参数的组合可保证,在任意脉冲方位角φJ作用下,只要初始角运动状态在Ω∀范围内,受控后的弹箭角运动仍可保持稳定。显然,上述有效脉冲参数组合,可直接用于非线性条件下的脉冲参数设计。
此外,当γ∀∈(0,1]时,有效脉冲参数组合如图8所示。竖线左边给出了满足式(53)第1式的脉冲范围,对应颜色的两条曲线所包围的区域给出了满足式(53)第2式的脉冲参数组合范围,二者的重合区域即为γ∀所对应的有效脉冲参数组合范围。由图8可见,当γ∀越小,有效脉冲参数组合所对应的范围越大。

图8 不同γ∀下的有效脉冲参数组合
将已知的rΩ(即式(50))代入式(43),计算可得不同γ∀对应的Ω∀的半径r∀,进而确定了α、β、α′、β′各自可取到的最大值,如图9所示。由于角运动方程式(27)的对称性,α和β的最大取值相等,α′和β′的最大取值相等。对于本节算例,当γ∀=0.068 6,α、β的最大值为3.06°,α′、β′的最大值为0.028°/cal。
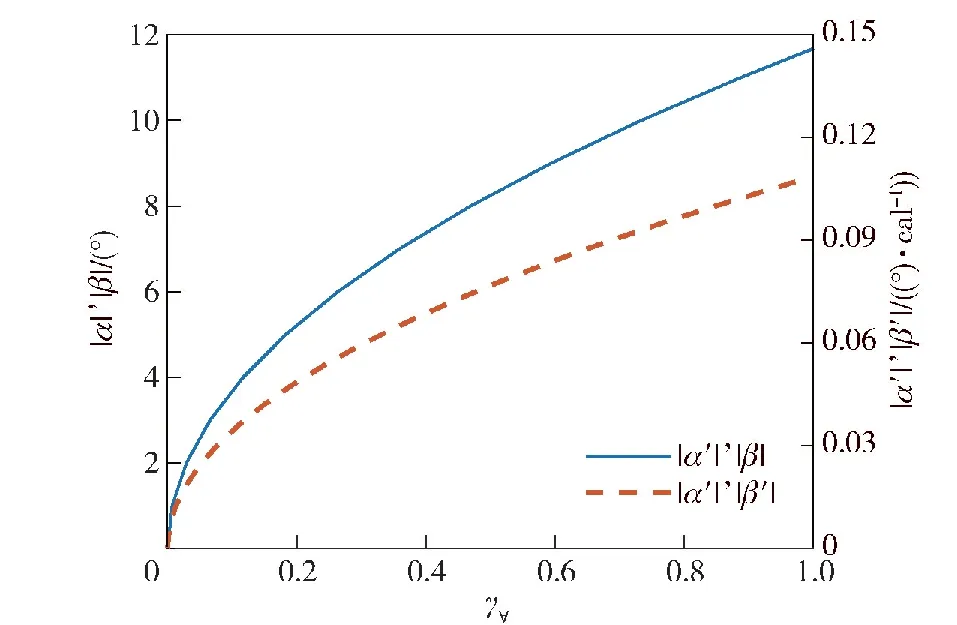
图9 γ∀与Ω∀中攻角和攻角速度最大值的对应关系
4 结论
本文探讨了平方和规划方法在弹箭角运动非线性吸引域估计中的应用。得到以下主要结论:
1)对于考虑高阶气动力系数的无控尾翼弹非线性平面角运动吸引域估计,通过构造李雅普诺夫函数,得到了高精度的吸引域估计结果,且李雅普诺夫函数的阶数越高,吸引域估计值与确切值越接近,验证了方法的可行性和有效性。
2)针对考虑了诸非线性气动力系数的脉冲末修迫弹空间角运动吸引域估计,通过构建高精度多项式近似模型开展平方和规划,对于采用二次李雅普诺夫函数的情形,吸引域估计结果与直接利用椭球几何关系所得结果一致,验证了方法的准确性。
3)由于脉冲作用主要影响弹箭的初始运动状态,故根据脉冲末修迫弹角运动的吸引域估计,可反算并确定出脉冲冲量及其轴向作用位置的有效组合范围(满足非线性稳定要求),由此得到非线性条件下脉冲参数设计的有效方法。
本文研究结果表明,平方和规划方法为弹箭角运动吸引域估计、非线性条件下的弹箭参数设计等提供了一个有力的工具,为后续更为深入的应用研究奠定了基础。
