Optimization of projectile aerodynamic parameters based on hybrid genetic algorithm
2015-03-29LIULinTIANXiaoliGAOXiaodongGANTaoyuanSHEXinji
LIU Lin, TIAN Xiao-li, GAO Xiao-dong, GAN Tao-yuan, SHE Xin-ji
(1. College of Mechatronic Engineering, North University of China, Taiyuan 030051, China;2.Yuxi Industrial Group Co., Ltd., Nanyang, 473000, China)
Optimization of projectile aerodynamic parameters based on hybrid genetic algorithm
LIU Lin1, TIAN Xiao-li1, GAO Xiao-dong2, GAN Tao-yuan2, SHE Xin-ji2
(1.CollegeofMechatronicEngineering,NorthUniversityofChina,Taiyuan030051,China;2.YuxiIndustrialGroupCo.,Ltd.,Nanyang, 473000,China)
Aerodynamic parameters are important factors that affect projectile flight movement. To obtain accurate aerodynamic parameters, a hybrid genetic algorithm is proposed to identify and optimize the aerodynamic parameters of projectile. By combining the traditional simulated annealing method that is easy to fall into local optimum solution but hard to get global parameters with the genetic algorithm that has good global optimization ability but slow local optimization ability, the hybrid genetic algorithm makes full use of the advantages of the two algorithms for the optimization of projectile aerodynamic parameters. The simulation results show that the hybrid genetic algorithm is better than a single algorithm.
projectile aerodynamic parameters; parameter optimization; hybrid genetic algorithm
Aerodynamic force of projectile is a major factor that affects the trajectory and speed of projectile when moving in the air. Thus, extracting the aerodynamic parameters of projectile from movement parameters based on system identification technology is a top priority. Among all existing methods, the three methods are famous: theoretical calculation method, wind tunnel experiment and range test. By comparison, theoretical method has the disadvantages of inaccurate calculation model and low accuracy; wind tunnel experiment usually uses shrinkage model to get the blowing data, which cannot reflect the actual ballistic parameters of projectile; but range test based on live ammunition shooting and optimization processing can get the real, accurate and optimized flight parameters of projectile.
Because traditional optimization method can easily fall into local optimum but cannot get the results accurately, this paper proposes a hybrid genetic algorithm with good global optimization ability. The optimization results of aerodynamic parameters of projectile show that this hybrid genetic algorithm is better than the conventional optimization algorithm.
1 Optimization algorithm
There are lots of optimization design methods, but none of them is universal due to their own limitations. The traditional optimization algorithm has higher computation efficiency and is over-dependent on mathematical model[1-6]. Convergence of optimization procedure is related to the choice of initial design points and it is easy to fall into local optimal solution and stagnation. Moreover, for such parameters optimization of projectile is a complicated system engineering, its mathematical model is very complex. Therefore, the choice of optimization algorithm is very strict[7-9]. The optimal solution obtained by traditional optimization algorithm is likely to be local optimum, but not global optimum. Conversely, genetic algorithm has good global optimization characteristics and can greatly avoid local optimal solution. In this case, the hybrid genetic algorithm is proposed by combining simulated annealing operation with genetic algorithm, and projectile parameters are optimized by making best use of the advantages and bypassing the disadvantages of the proposed algorithm.
2 Hybrid genetic algorithm
The basic flow chart of hybrid genetic algorithm is shown in Fig.1.

Fig.1 Flow chart of hybrid genetic algorithm
The hybrid genetic algorithm can be encoded in different ways. This paper adopts binary code, and its string length depends on the desired accuracy. For example, the range of design variableXiis [ai,bi] with the accuracy of 10-5, then the range should be divided into (bi-ai)×106. Assuming that the string length ofXiismi, then there is 2mi-1=(bi-ai)×106=2mi-1.
Fitness function is the function which evaluates individual’s fitness level according to encoding. Different forms of fitness function can be used for the same problem. The objective function can be defined directly as the fitness function. In this paper, the residual sumεcxof sample trajectory data and optimized calculation ballistic data is set as the objective function. The objective function expression of drag coefficient optimization model is
wherexciis the data of thei-th projectile ballistic trajectory point inxdirection from flying measurement data, andxiis the data of thei-th projectile trajectory point inxdirection from simplified projectile trajectory calculation program. Other variables have similar meanings.
Two major kinds of termination conditions of genetic algorithm are fitness value determination and evolutionary generation determination. The former is terminated when average fitness value or maximum fitness value exceeds the default value. The latter is terminated when evolutionary generations exceed the default generations.
In proportional selection operation, according to the fitness values, the excellent individuals are selected as male parents for crossover operation, where the two individuals act as crossover of gene chain code to generate new individuals, as shown in Fig.2.

Fig.2 Crossover operation
Mutation operation is mainly responsible for improving local search capability of genetic algorithm and maintaining diversity of the groups, which can prevents “prematurity”. A certain bit in the gene chain is randomly selected, and the gene code is flipped (0→1, 1→0).
Although mutation operation is added for local search of genetic algorithm, when evaluating the fitness values, that is evaluating the objective function, only the individuals whose objective function values decrease can be accepted, but the algorithm is still inclined to fall into “prematurity” and obtains a local optimal solution.
To solve this problem, simulated annealing operation is introduced. When the object reaches heat balance during the annealing, the probability with the system energyEcan be expressed by
Simulated annealing operation allows individuals with ascending objective functions to be accepted at a probability of exp(-E/kBT), which generates random numberrandwith a uniform distribution in the interval of [0,1]. If exp(-E/kBT)>rand, the individuals are also accepted. Thus the local optimal solution can be avoided.
3 Optimization model
For a certain model, an input corresponds to an output. Since the projectile model consists of a set of highly nonlinear differential equations, an output corresponds to an input. For the optimization of aerodynamic parameters, the values of aerodynamic parameters are constantly changed and then new projectile data are got. By comparing the calculated trajectory with the sample trajectory, when the two trajectories are exactly the same, the values of aerodynamic parameters become the optimal solutions theoretically. For the optimization model in this paper, hybrid genetic algorithm is used to change the initial values of aerodynamic parameters. Because 2D ballistic model is established , the related aerodynamic parameter only involves drag coefficientCx. The optimization process is shown in Fig.3.

Fig.3 Optimization process of drag coefficient Cx
4 Simulation results
The 2D projectile model is programmed in C language, the variables of the projectile equation with four degrees of freedom change slowly. The integral step is similar to the particle trajectory, and can be generally set at about 0.1 s.
In simulation calculation, in order to verify the practicability of the proposed hybrid genetic algorithm to identify aerodynamic parameters, there must be a set of sample data whose true values are known. In this paper, a group of known drag coefficients are introduced into the projectile equations to get a set of projectile data which are assumed to be the sample data with known true values. The initial values of the design variables for the optimization are derived from theoretical calculation.
For a certain type of trajectory correction projectile, the above optimization model, simulated annealing algorithm, genetic algorithm and hybrid genetic algorithm are used to optimize and calculate the drag coefficient, respectively.
The simulation results are compared in Table 1, and the optimization results are shown in Fig.4.

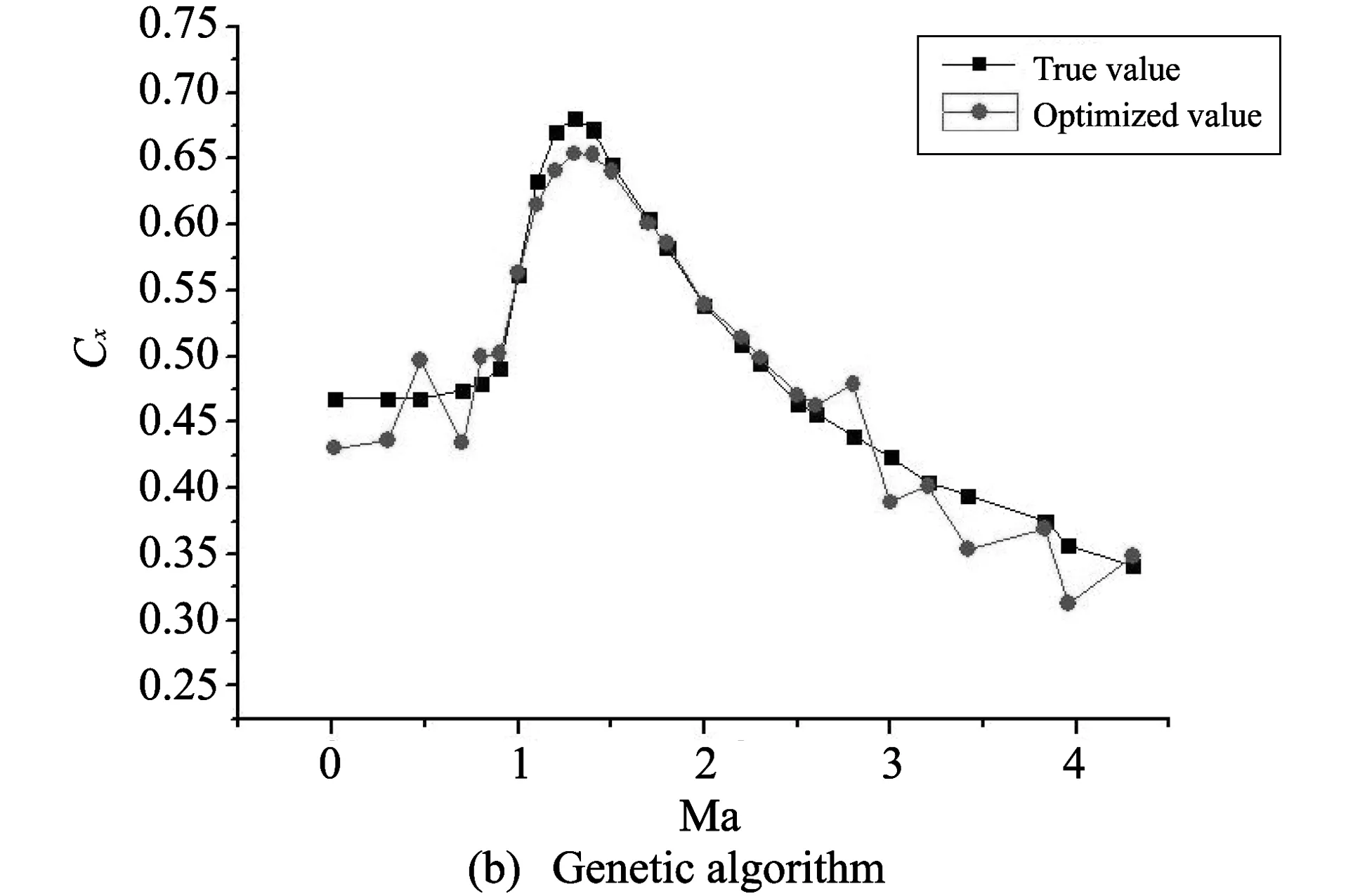

Fig.4 Comparison of optimization results
By comparing the curves of three optimization algorithms shown in Fig.4, it can be seen that the drag coefficient obtained by the hybrid genetic algorithm is closer to the true value.

Table 1 Comparison of three algorithms
It can be seen from Table 1 that the genetic algorithm has the longest time and is trapped in local optimal solution. Simulated annealing algorithm is better, but the time of the parade is too long. The hybrid genetic algorithm is better than the genetic algorithm and simulated annealing algorithm in optimization speed and effectiveness and is a better algorithm for the optimization of the aerodynamic parameters of projectile.
5 Conclusion
In this paper, a hybrid genetic algorithm is proposed for extracting the aerodynamic parameters of projectile and rocket. Introducing the simulated annealing algorithm into the traditional genetic algorithm can effectively avoid “prematurity” of the genetic algorithm and termination of calculation. But the hybrid genetic algorithm is not conducive to higher optimization efficiency. Therefore, it can be investigated further by combining the direct search method with the proposed hybrid genetic algorithm to improve optimization efficiency.
[1]WAN Min, WANG Xiao-peng. A genetic algorithm based identification method for dynamical systems. Flight Dynamics, 2003, 21(2): 56-58.
[2]LI Xu-wu, WANG Xiao-ping. Genetic algorithm-theory, application and software to achieve. Xi’an: Xi’an Jiaotong University Press, 2002.
[3]CAI Jin-shi. Identification of aircraft systems. Beijing: Aerospace Press, 1995.
[4]HAN Zi-peng. Rocket exterior ballistics. Beijing: Beijing Institute of Technology Press, 2008.
[5]ZHOU Ming-sun, SHU dong. Principle and application of genetic algorithm. Beijing: National Defense Industry University Press, 1998.
[6]WANG Hai-tao, GUO Shu-wei, GUO Peng, et al. Application of genetic algorithms for aerodynamic parameter estimation of large parachute. Journal of Astronautics, 2010, 31(4): 981-985.
[7]JI Ya-xin. Study on the optimization method of the aerodynamic parameters of projectile and rocket. Taiyuan: North University of China, 2013: 29-50.
[8]LIU Shu. Investigation on methods of characteristic parameters identification using flight data for projectiles. Taiyuan: North University of China, 2013: 40-65.
[9]BAI Ge, ZHANG Hai-tao, LIU Cui-ping, et al.WSN broadcast algorithm based on genetic simulated annealing algorithm. Computer Measure and Control, 2013, 21(11): 3053-3056.
基于混合遗传算法的弹箭气动参数优化
刘 霖1, 田晓丽1, 高小东2, 甘桃元2, 佘新继2
(1. 中北大学 机电工程学院,山西 太原 030051; 2. 豫西工业集团有限公司, 河南 南阳 473000)
弹箭气动参数是影响弹箭飞行运动的重要因素。 在弹箭气动参数优化过程中, 传统优化方法容易陷入局部最优解。 为此, 提出了混合遗传算法用于弹箭参数优化。 它将传统模拟退火方法与遗传算法全局搜索能力相结合。 仿真结果表明, 混合基因算法比单一算法优化效果好。
弹箭气动参数; 参数优化; 混合遗传算法
LIU Lin, TIAN Xiao-li, GAO Xiao-dong, et al. Optimization of projectile aerodynamic parameters based on hybrid genetic algorithm. Journal of Measurement Science and Instrumentation, 2015, 6(4): 364-367.
10.3969/j.issn.1674-8042.2015.04.010
LIU Lin (56349140@qq.com)
1674-8042(2015)04-0364-04 doi: 10.3969/j.issn.1674-8042.2015.04.010
Received date: 2015-07-23
CLD number: TJ413 Document code: A
猜你喜欢
杂志排行
Journal of Measurement Science and Instrumentation的其它文章
- Design of intelligent distinguishing system for slot machine based on PLC
- Design of speed controller for electronic fuel injection gasoline generator based on feed-forward PID control
- Handover algorithm for multiple networks based on Bayesian decision
- Symmetric axis detection for images based on Hough algorithm
- Effects of interior ballistic factors on dispersion of central blast tube cluster munitions
- Uncertainty contribution at NIS phototherapy irradiance facility
