勾股定理的扩展

广西兴业县沙塘镇福联小学(537822) 李桥飞

勾股定理的扩展

广西兴业县沙塘镇福联小学(537822) 李桥飞

在我国古代人们将直角三角形中短的直角边叫做勾,长的直角边叫做股,斜边叫做弦.人们已经知道,如果勾是3,股是4,那么弦就是5.后来人们进一步发现并证明了直角三角形三边的关系:两条直角边的平方和等于斜边的平方.

a:当勾为奇数时,即2n+1,股为2n(n+1),那么弦就是2n(n+1)+1(n≥1的整数)

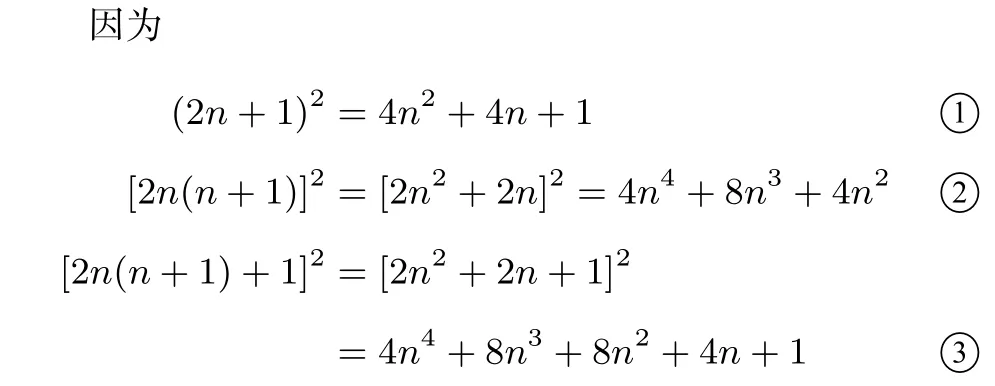
所以:①+②=③上式满足勾股定理即(2n+1)2+(2n2+ 2n)2=(2n2+2n+1)2

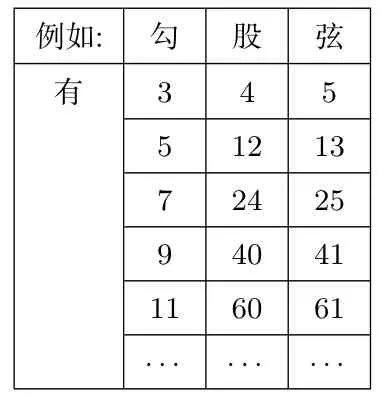
_例如:__ _勾_ __股_ __弦_有____3__ __4__ __5__ ____5__ __12_ __13_ ____7__ __24_ __25_ ____9__ __40_ __41_ _11__ __60_ __61_ _______ _____ _ _____··· ···_ _···_

b:当勾为偶数时,即2n,股为n2−1,那么弦就是n2+1 (n≥3的整数)

即(2n)2+(n2−1)2=(n2+1)2也同样满足勾股定理.

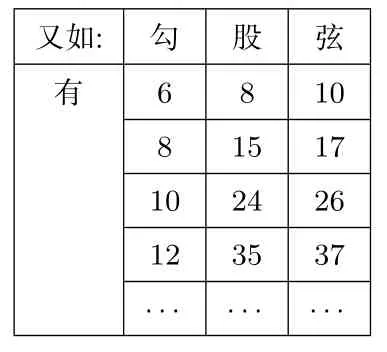
_又如:__ _勾_ __股_ __弦_有____6__ __8__ _10_ ____8__ __15_ __17_ _10__ __24_ __26_ _12__ __35_ __37_ _______ _____ _ _____··· ···_ _···_

在众多的勾股弦数组中,唯一有勾3、股4、弦5的数组是连续的自然数数组.且32+42=52这个式子表明在自然数中有三个连续自然数,使得前两个自然数的平方和等于后一个自然数的平方和.再有:102+112+122=132+142,这个式子表明在自然数中有五个连续自然数,使得前三个自然数的平方和等于后两个自然数的平方和.还有212+222+232+242=252+262+272,同理在自然数中有七个连续自然数,使得前四个自然数的平方和等于后三个自然数的平方和.看:

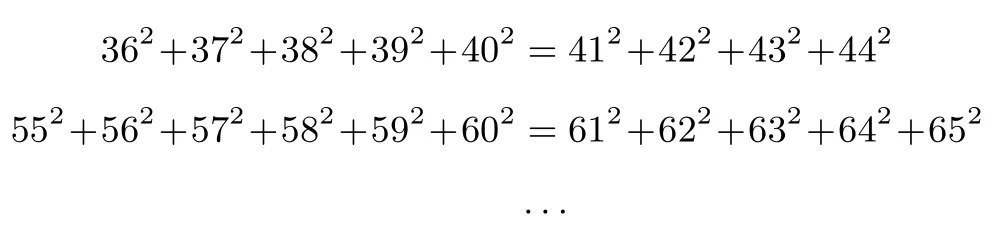
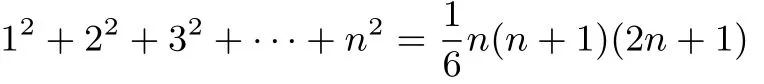
从而命题得证(2n2+n)2+···+(2n2+2n)2=(2n2+2n+ 1)2+···+(2n2+3n)2成立.即命题为:在自然数的数集中,存在(2n+1)个连续自然数,使得前(n+1)个连续自然数的平方和等于后n个连续自然数的平方和.