基于增广Lyapunov 泛函的时变时滞T-S模糊系统稳定性分析

龙奕璇，肖伸平

（1. 湖南工业大学 电气与信息工程学院，湖南 株洲 412007；2. 电传动控制与智能装备湖南省重点实验室，湖南 株洲 412007）

1 研究背景

近几十年来，T-S 模糊模型得到了学者们的广泛研究，这是因为它通过将局部线性模型与模糊隶属函数相结合，可以有效地描述非线性系统[1]。众所周知，T-S 模糊系统不可避免地会存在时滞现象，而时滞的存在可能会导致系统性能恶化或者不稳定，而系统的稳定性是保证控制系统正常运行的基石[2-6]。因此，对T-S 模糊系统中的时滞问题进行研究显得至关重要。

虽然对系统进行稳定性分析的方法有很多，但是能够有效地应用于线性、非线性、时不变和时变系统的方法只有李雅普诺夫泛函方法。基于该方法分析时滞系统的稳定性问题时，其首要任务是选择合适的李雅普诺夫泛函。常见的李雅普诺夫泛函构造方法包括增广李雅普诺夫泛函法[7]、时滞分段李雅普诺夫泛函法[8]，以及时滞乘积型李雅普诺夫泛函法[9]。其次，需要对李雅普诺夫泛函求导后产生的积分项进行准确地估计。比较有效且流行的估计方法是积分不等式法，常用积分不等式主要包括Jensen 不等式[10]、Writinger 不 等 式[11]、Bessel-Legendre 不等式[12]、自由权矩阵积分不等式[13]。目前，这些方法已被应用到时滞T-S 模糊系统的研究中。例如，文献[14]采用了增广李雅普诺夫泛函方法与线积分李雅普诺夫函数的方法，研究了时变时滞T-S 模糊系统的稳定性和镇定性问题，但是对泛函求导后的积分项进行估计时，仍然使用了具有一定保守性的Writinger 不等式。文献[15]在李雅普诺夫泛函中引入了时滞乘积项，并且运用了改进逆凸不等式方法，放宽了泛函的正定条件。文献[16]采用二阶时滞乘积方法，在泛函中引入了二阶时滞乘积项，使构造的李雅普诺夫泛函包含更多的有效信息。由此可见，一个合适的李雅普诺夫泛函直接影响着系统稳定性判据的保守性。

综上所述，本文拟对时变时滞T-S 模糊系统进行稳定性研究。为了得到较小保守性的稳定性判据，首先，利用增广李雅普诺夫泛函方法与线积分李雅普诺夫函数，构造一个能捕捉到更加有效时滞信息的泛函。然后，运用估计精度更高的广义自由权矩阵积分不等式方法处理由李雅普诺夫泛函求导后产生的积分项，从而得到了一个保守性更低的三阶时滞依赖的稳定条件。最后，通过三阶矩阵多项式的判定方法，将此稳定条件转化为线性矩阵不等式的形式。

整文采用如下标号，Rn表示实数域的n维向量空间；Rn×m和Sn分别表示n×m维实矩阵和n×n对称矩阵；上标‘T’和‘-1’分别表示矩阵的转置和逆；diag{}表示对角阵；0 表示具有适当维数的零矩阵；*表示矩阵中的对称项；Sym{A}=A+AT。

2 问题描述

3 主要结论

4 数值实例

本节中，将提供两个数值实例来验证所使用方法的优越性和有效性。

例1考虑带有以下系统矩阵的系统（3）：

对于不同的时滞导数上界µ=µ1=-µ2，表1 列出了基于定理1、推论1 和其他现有稳定性判据所得到的最大允许时滞上界，其结果如表1 所示。

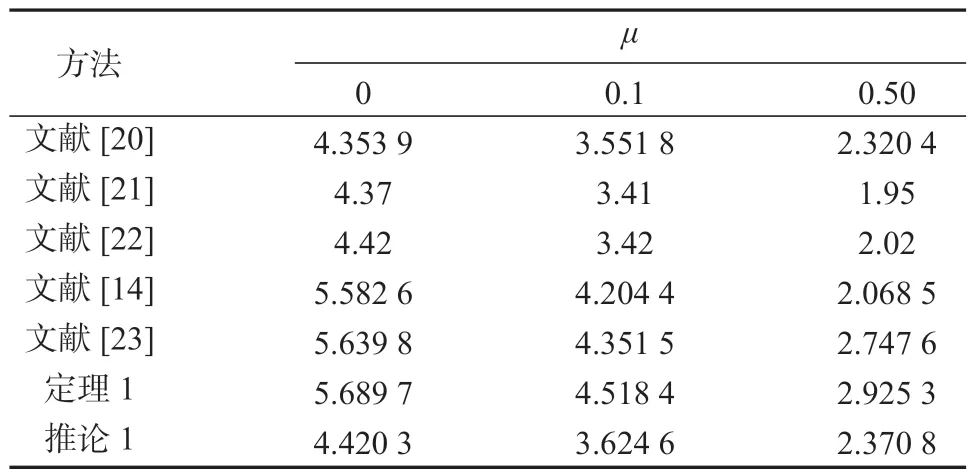
表1 例1 中不同μ 下得到的最大时滞允许上界Table 1 Maximum allowable upper bound of delays with different μ values in example 1

从表1 可以看出，定理1 计算出的最大时滞允许上界最大，这说明本文提出的稳定性判据具有较小的保守性。通过比较定理1 和推论1 的数值结果可与看出，基于定理1 所得到的最大允许时滞上界更大，这说明了本文引入的线积分李雅普诺夫函数Va(t)和增广李雅普诺夫函数Vb(t)有利于降低稳定性判据的保守性。

例2考虑带有下列系统矩阵的系统（3）：

表2 列出了通过各种方法计算出的最大允许延迟上界。不难看出，对于不同的时滞上界导数μ=μ1=-μ2，基于定理1 所得到的最大允许时滞上界高于其它的稳定性判据，这再次说明本文所提出的方法且具有一定的优越性。

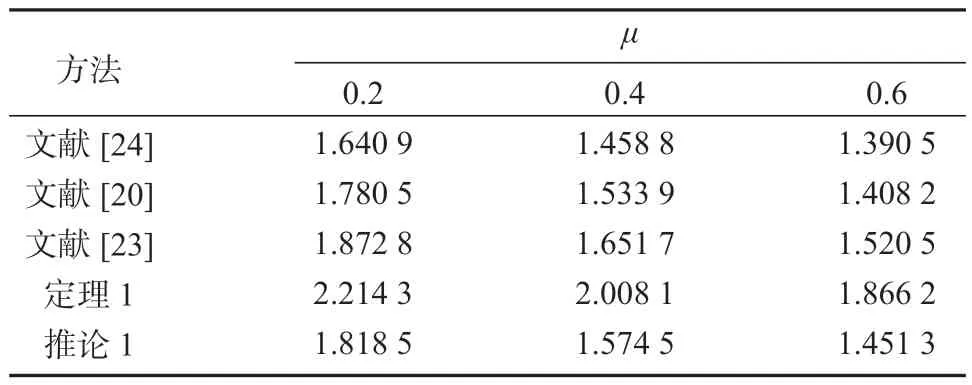
表2 例2 中不同的μ 下得到的最大时滞允许上界Table 2 Maximum allowable upper bound of delays with different μ values in example 2

5 结语

采用李雅普诺夫理论对含有时变时滞的T-S 模糊系统进行稳定性分析。通过构造一个包含更多时滞有效信息的李雅普诺夫泛函，并结合估计精度更高的广义自由权矩阵积分不等式，得到了一个新的保守性更低的稳定性判据。再利用三阶矩阵不等式方法将其转化为线性矩阵不等式的形式。最后，通过两个实例验证了本文方法的优越性。