基于有限差分法的复合系泊链缆动力模型及其验证

李欣怡，于立伟

（中国海洋大学 工程学院，山东 青岛 266100）

随着越来越多的深水和超深水油气资源被发现，深水油气资源开发已成为全球的热点。然而，随着水深的增加，平台需要更长的锚链来进行系泊，这对于自重过大的传统钢制系泊链来说将非常困难。而合成纤维系泊链具有质量轻、系泊半径小、轴向刚度低且可降低一阶波频张力的特点，有较好的系泊性能，因而被广泛用于深水系泊中。在合成纤维系泊中，聚酯纤维系泊被广泛使用，其制造和安装规范也比较成熟。聚酯缆绳与传统钢缆的参数比较见表1。

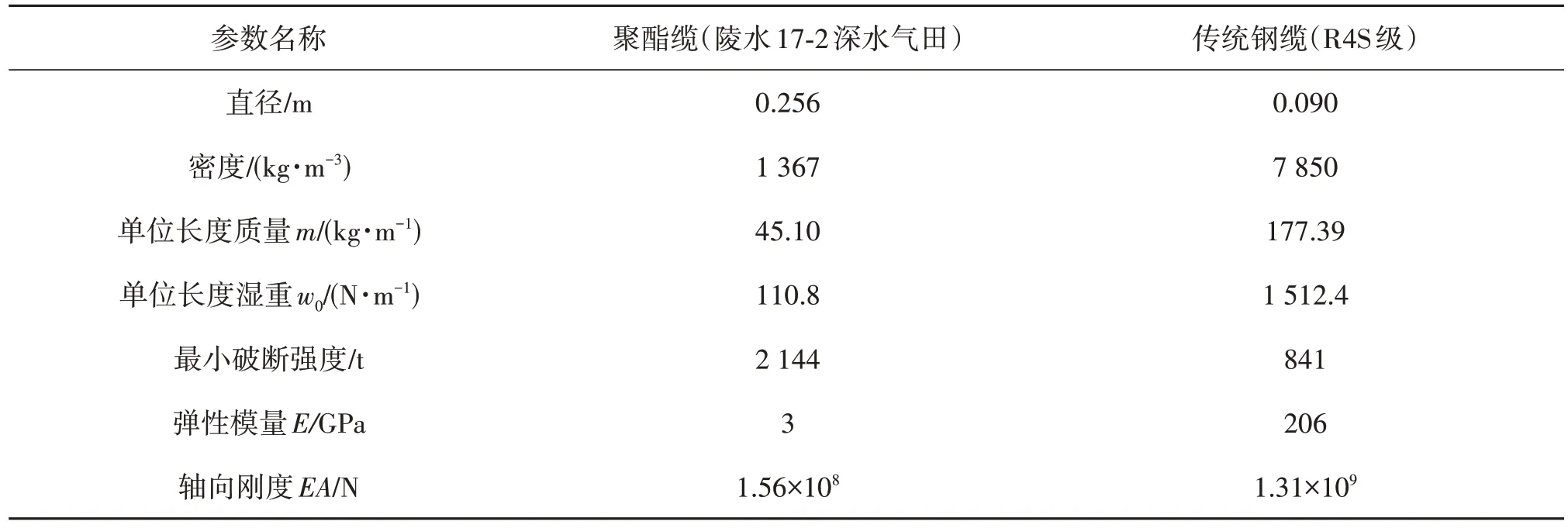
表1 聚酯缆和传统钢缆的参数Tab.1 Parameters of polyester cable and traditional steel cable

由于纤维系泊材料的非线性以及复杂的黏弹性和黏塑性特性，使得其力学性能复杂，与传统的钢铁材料完全不同，这给其模拟和分析带来困难。其力学性能主要包括最小断裂强度、动刚度、蠕变、蠕变恢复、蠕变断裂和疲劳破坏等，其中刚度一直是学者们关注的重点。Del Vecchio［1］进行了合成缆刚度测试试验，并以具体刚度模量计算结果为因变量，以平均载荷、载荷振幅和周期的对数为自变量，进行线性回归分析，得到了不同的比模量回归方程。Fernandes 等［2］对小直径聚酯缆和直径为5 英寸（0.127 m）的实际大直径聚酯缆进行了动刚度测试，结果表明，平均荷载和荷载幅值对刚度有较大影响，而荷载频率对平行结构缆绳的影响可以忽略不计。同时基于数据进行了线性回归，并通过修正得到了无量纲的动刚度经验公式。Bosman 和Hooker［3］进行了随机加载和动态拉伸试验，结果发现，动刚度经验公式对小尺寸缆绳和全尺寸聚酯缆的动刚度测试都可做出很好的预测。Davies等［4］分别对聚酯、芳纶和高强聚乙烯（HMPE）缆绳进行了全尺寸试验研究，其中包含静刚度测量、低荷载和高荷载下的动刚度测量，以及一个蠕变循环。据试验发现，所有材料的刚度都随着加载幅值的增加而减小，而加载周期的影响却非常小，HMPE 绳约为10%～15%，芳纶绳约为5%，聚酯缆甚至更小。Davies 等［5］采用弹性回复法对芳纶绳和HMPE 绳进行了拉伸试验，发现缆绳的动刚度在初始阶段增加较快，一段时间后趋于一个定值。HMPE绳对这些影响动刚度的参数比芳纶绳更加敏感，在卸载时有更大的残余应变和滞后，且循环过程中HMPE 绳的阻尼也更高。Liu 等［6］系统地研究了聚酯、Aramid和HMPE 三种合成纤维缆在循环载荷下的非线性行为，并基于实测数据提出了一个同时考虑平均张力、应变幅值和荷载循环次数的经验表达式。Liu等［7］对聚酯和HMPE系泊缆进行了系统的试验研究，了解受损合成纤维系泊缆动态刚度的演变，试验结果表明，动刚度随平均张力和载荷循环次数的增加而增加，随应变幅值和损伤程度的增加而减小。同时，Liu等［7］提出了一个考虑损伤效应、平均张力、应变幅值和加载循环次数的经验表达式来描述损伤对合成纤维缆动刚度的影响，其中系数由最小二乘法确定，测量数据和经验表达式计算结果的比较显示了良好的一致性。Wibner 等［8］基于目前可用的试验数据，利用动刚度值的上下限方法对聚酯绳的全尺寸特性进行估算。Huang 等［9］基于Schapery 理论和Owen 流变学理论，提出了一种新的应力—应变本构模型，该模型能够很好地模拟非线性循环荷载作用下合成纤维缆的时变特性。乔东生和欧进萍［10］基于Del Vecchio［1］提出的动刚度经验公式，用迭代法计算链—缆—链结构的刚度，并对复合锚泊线的动力特性进行比较分析。

目前，常用的系泊缆动力分析模型有集中质量模型和细长杆模型［11］。在集中质量模型中，系泊缆在建模的最开始被离散化，并由有限长度的无质量单元连接在一起的点质量代替，如图1所示。可直接从牛顿运动定律导出常微分方程，并通过数值算法求解。集中质量—弹簧模型有以下优点：1）模型简单，物理含义明确；2）系泊缆求解实现容易；3）应用条件不受系泊缆特性和波流状况的影响。其难点在于弹簧刚度、阻尼系数、附加质量系数等参数的确定，当使用完全动态解时，会出现振荡效应，导致多解。

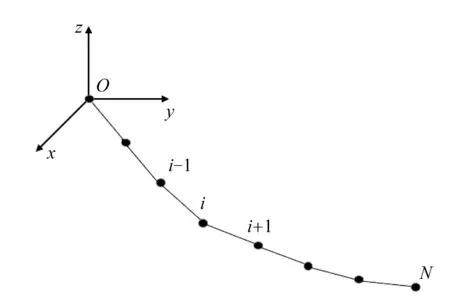
图1 集中质量—弹簧模型Fig.1 lumped-mass-and-spring model

细长杆模型包含有限元方法和有限差分法两种求解方法。有限元方法方面，Garrett［12］首先提出了一种等主刚度不可伸直的弹性杆的三维有限元模型，如图2所示。由于杆具有弹性和任意的几何形状，细长杆可以承受水下各种载荷和拉力。载荷包括由杆的运动和外部流体运动引起的水动力及重力。结合杆的经典理论［13］和Nordgren［14］的研究，根据线性动量守恒和角动量守恒，忽略转动惯量和剪切变形的影响，得到以矢量形式给出的非线性运动方程。用伽辽金法将偏微分方程组简化为常微分方程组进行求解。该模型有以下优点：1）应用范围广，可用于解决海洋工程领域的静态和动态问题；2）描述简单，采用矩阵形式表达，便于编写计算机程序；3）计算结果稳定且收敛。但往往在建模和求解过程中需要大量时间，且在三维空间的几何大变形动力学问题方面存在一定不足。

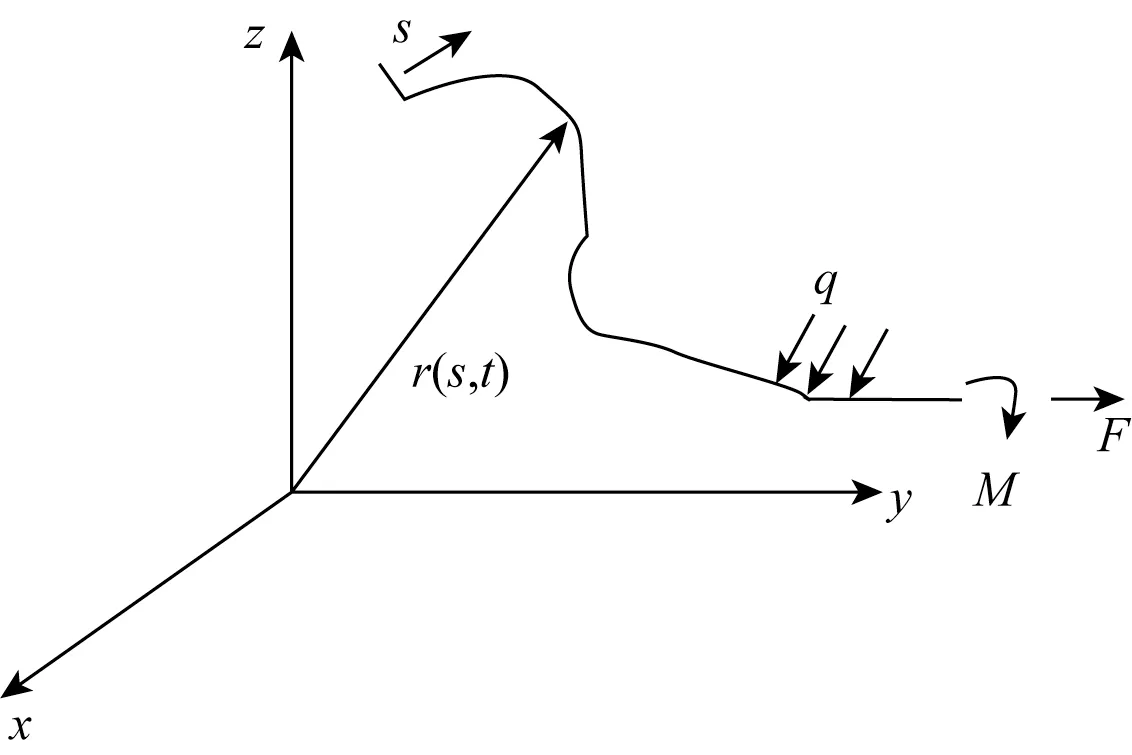
图2 细长杆模型Fig.2 Slender-rod model

对于有限差分法，通过对杆单元动力学偏微分方程的直接有限差分离散进行求解，通常包含了显式和隐式两种格式。一般而言，隐式离散方法比显式更可取，因为隐式方法对于长时间模拟更稳定、更准确，并允许较大的时间步长，这使得隐式方法更适合于系泊缆的断裂后行为或拖曳应用模拟。通常采用Box 方法进行隐式有限差分，Wendroff［15］证明了该方法在空间和时间上都是二阶的，并且是无条件稳定和收敛的。该方法需要解析计算方程组的雅可比矩阵，这需要大量的工作，但生成的代码非常强大，并根据所需的精度，在每个时间步长迭代2到5次后即可收敛。该方法更加适用于空间大变形的缆结构和具有非线性应力应变关系的复合材料缆的数值模拟。

对于有限元法和有限差分法，两者都是通过离散的方式求解微分方程，但离散方式不同，有限元法是用插值函数来近似微分，而有限差分是用差分近似。在实际应用中，有限元方法主要在求解结构强度等椭圆型方程中适合，对带有非定常时间项的方程求解有一定局限性，计算时间较长。而有限差分法简单、灵活、通用性强，利用差分网格构造出高精度解，求解速度较快。因此文中采用有限差分法，把控制方程中的导数用网格节点上的函数值的差商代替进行离散，保证了求解精度的同时也最大限度地加快了运算速度。

文中基于细长杆模型，采用有限差分法建立可以考虑链—复合纤维缆—链结构动静刚度的复合系泊链缆动力模型，并对该模型的准确性开展验证研究。根据已有算例和在波浪水槽中进行单根钢链模型试验，验证了数值模型应用于全链的准确性。对于复合系泊链缆，通过静刚度和动刚度迭代，将数值模拟结果与算例结果进行比较，验证了数值模型应用于链—缆—链结构的准确性。

1 系泊链缆动态模型

1.1 单根系泊缆的模型

文中采用最早由Tjavaras［16］提出的系泊缆有限差分动力模型，将其应用到具有链—缆—链结构的复合系泊链缆的数值模拟中。该模型由10个关于应变、力、速度和曲率的偏微分控制方程组成，方程保留了惯性项和弯曲刚度项。使用欧拉参数来描述拉格朗日参考系的相对旋转，不受欧拉角公式奇异性的影响。模型中采用隐式有限差分法对由欧拉参数描述产生的控制方程进行离散化。

首先，建立两个坐标系，即弧坐标系和大地坐标系，如图3 所示，其中前者以弧长s为变量，单位向量为a=(τ，n，b)，后者为笛卡尔坐标系，单位向量为b=(i，j，k)，这两个坐标系有如下关系：

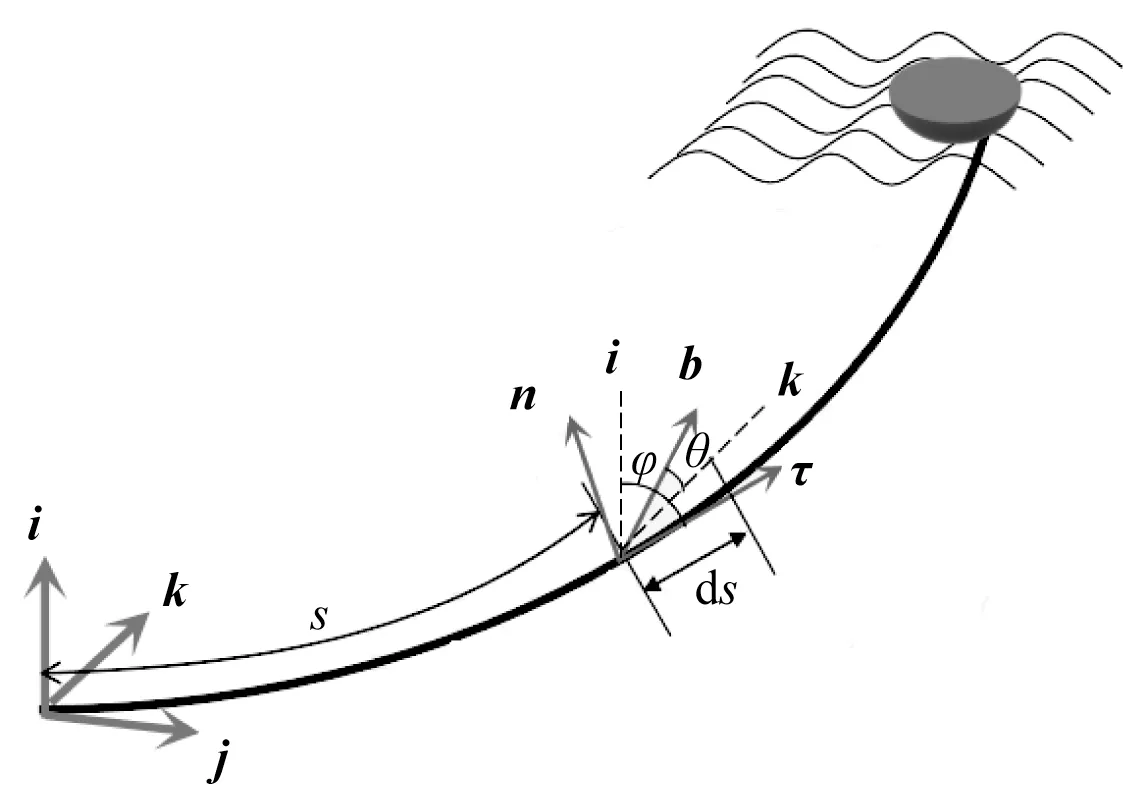
图3 坐标系Fig.3 Coordinate systems

式中：θ为系泊切线的外平面角，φ为系泊切线的内平面角。

那么，基于对锚泊线无限小段的动力学分析，系泊锚链的动力模型可以用一阶偏微分方程组来描述，如图4所示。

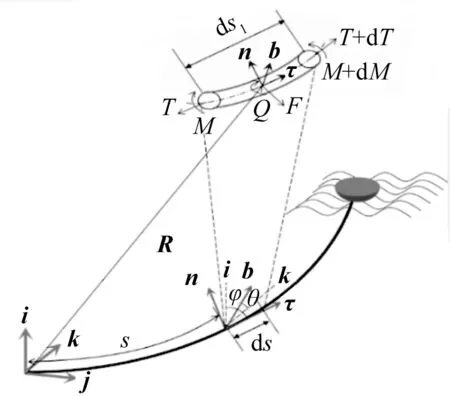
图4 锚链动力模型Fig.4 Steel chain dynamics model

在动力模型中包含了力平衡方程、力矩平衡方程、兼容性方程和曲率方程，具体如下所示：式中：ω1、ω2、ω3分别为角速度的扭转分量、法向（面外）分量、副法向（面内）分量；u、v、w分别为系泊单元的切向速度、法向速度、副法向速度；f(ε)为张力—应变关系；ε为应变；Sn、Sb分别为剪力的法向、副法向分量；E为杨氏模量，GPa；G为剪切模量；I为系泊横截面的平面惯性矩；IP为系泊横截面的极惯性矩；Mt，Mn，Mb分别为大地坐标系中内力矩矢量的切向、法向、副法向分量。

上述方程包含10个未知变量，即：

这些方程可以用矩阵形式写成偏微分方程组：

式中：Y为因变量向量。

如图5 所示，采用有限差分Box 法进行时间和空间的离散化，np个节点将锚链空间离散成np−1 个单元，其中心差分对应：

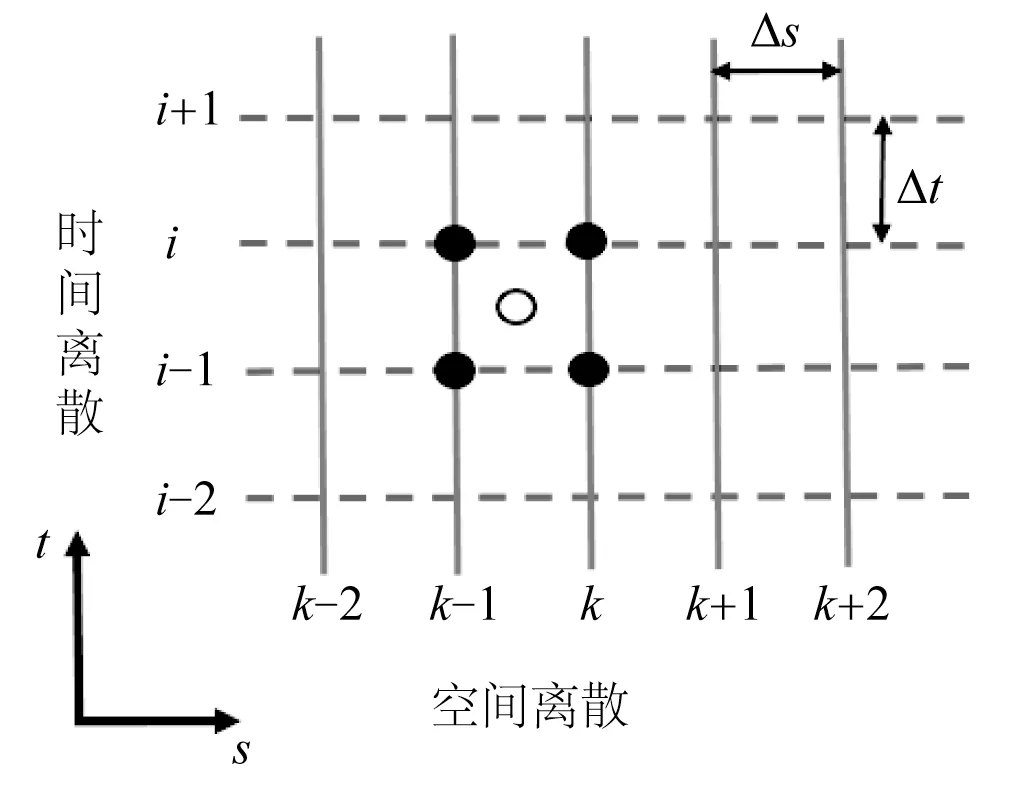
图5 有限差分法Fig.5 Finite difference method

代入方程组得到如下离散矩阵方程：

该矩阵包含10（np−1）个方程和10np个未知数。在k=1（锚点）和k=np（导缆孔）处添加边界条件，锚链在运动的过程中，满足锚点和导缆孔处的曲率为零，锚点处速度为零，即：

导缆孔处的速度与上部刚性浮体在导缆点处的速度相等，即：

最终采用松弛法求解矩阵，即可得到未知变量，实现系泊缆的数值模拟。

1.2 合成纤维缆的刚度求解方法

对于合成纤维缆，其应力应变关系f（ε）为非线性，Del Vecchio［1］和Fernandes［2］推导出了在循环荷载作用下合成纤维缆的杨氏模量计算公式：

式中：α′，β′，γ′为与材料特性有关的参数；Lm为平均张力与最大破断张力（MBL）的比率；La为动张力变化幅值与MBL的比率。

如图6所示，采用迭代法［10］求解合成纤维缆的静态和动态刚度，迭代步骤为：

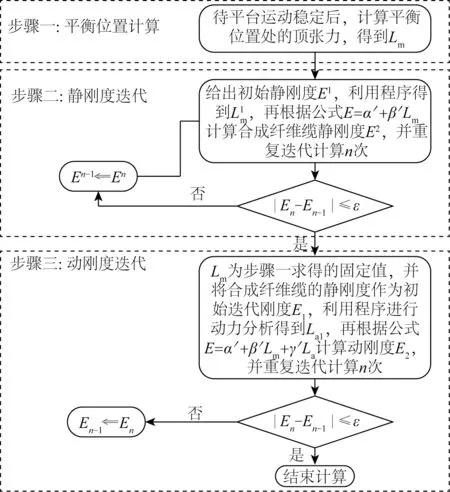
图6 合成纤维缆动刚度计算程序的实现Fig.6 Implementation of the procedure for calculating the dynamic stiffness of synthetic fiber cables

1）计算上部平台在定常风、流和二阶波浪力荷载作用下的运动响应，得到上部平台的初始平衡位置，此时导缆孔处的张力就是合成纤维缆顶端的初始预张力。合成纤维缆顶端的初始预张力为平均张力Lm。

2）求解合成纤维缆的静刚度，即合成纤维缆在初始平衡位置时的刚度（此时La=0）：预先给定合成纤维缆的初始迭代刚度E1，并计算合成纤维缆在初始平衡位置的顶张力Lm1，然后利用式（18）计算得到合成纤维缆的刚度E2，并重新计算合成纤维缆在初始平衡位置的顶张力Lm2，重复迭代计算n次，直到满足|En−En−1|≤ε时停止迭代（ε为预先给定的容差），并将计算结果En作为合成纤维缆的静刚度。

3）求解合成纤维缆的动刚度，即合成纤维缆围绕平衡位置做给定简谐振动时的刚度（此时Lm为步骤1）求解得到的固定值）：将合成纤维缆的静刚度作为初始迭代刚度E1，给定合成纤维缆顶端简谐运动时程后进行动力分析，并计算合成纤维缆的动张力变化幅值La1，利用式（18）计算得到合成纤维缆的刚度E2，重新进行动力分析后计算得到合成纤维缆的动张力幅值变化La2，重复迭代计算n次，直到满足|En−En−1|≤ε时停止迭代（ε为预先给定的容差），并将计算结果En作为合成纤维缆的动刚度。

对于由“链—合成纤维缆—链”结构组成的复合系泊链缆，在全链程序的基础上，将复合系泊链缆按照材料种类进行分段，并将每一段的参数写入到对应杆离散单元中，再结合合成纤维缆的静刚度和动刚度迭代步骤，将迭代式（18）、对应的参数和迭代过程通过程序实现。在迭代过程中，每次迭代计算用到的轴向刚度均来自于上一次迭代，并在每次迭代过后输出顶张力和轴向刚度，以便应用图6的迭代过程进行动静刚度迭代。

基于杆单元模型采用有限差分法建立了具有链—合成纤维缆—链结构的复合系泊链缆数值模型，下面将其应用于全钢链和链—缆—链结构复合系泊链缆的数值模拟中，并将模型试验和算例结果进行对比验证。

2 全钢链的模型验证

为了验证系泊链缆数值模型在全钢链模拟中的准确性，进行了钢链的算例验证和模型试验验证。

2.1 钢锚链算例模拟与验证

2.1.1 试验设置

采用Azcona 等［17］的单根钢锚链模型试验结果进行数值模型的验证。试验布置如图7所示，波浪水槽的尺寸为50 m×30 m×5 m（长×宽×高）。单根钢锚链浸没在水池中，形成悬链线形状，底端锚点固定在水槽底板上，顶端系缆点通过测力计连接到驱动器。试验过程中，系缆点在驱动器的激励下在悬链线平面内绕平衡位置做水平方向的正弦往复运动。锚链参数如表2所示，试验工况设置如表3所示，工况中选取了两种不同的锚链水平跨距配置，每种配置下进行了1个静态工况和3个不同周期动态工况的试验。

图7 试验布置示意Fig.7 Schematic diagram of the cases model

表2 锚链参数Tab.2 Steel chain parameters

表3 试验工况Tab.3 Experimental cases

2.1.2 算例结果及验证

将各工况结果和数值模拟结果做对比，如图8～10和表4所示，其中图8和表4为工况1和2的2种静态工况的对比结果，图9为配置1锚链动态工况的对比结果，图10为配置2锚链动态工况的对比结果。

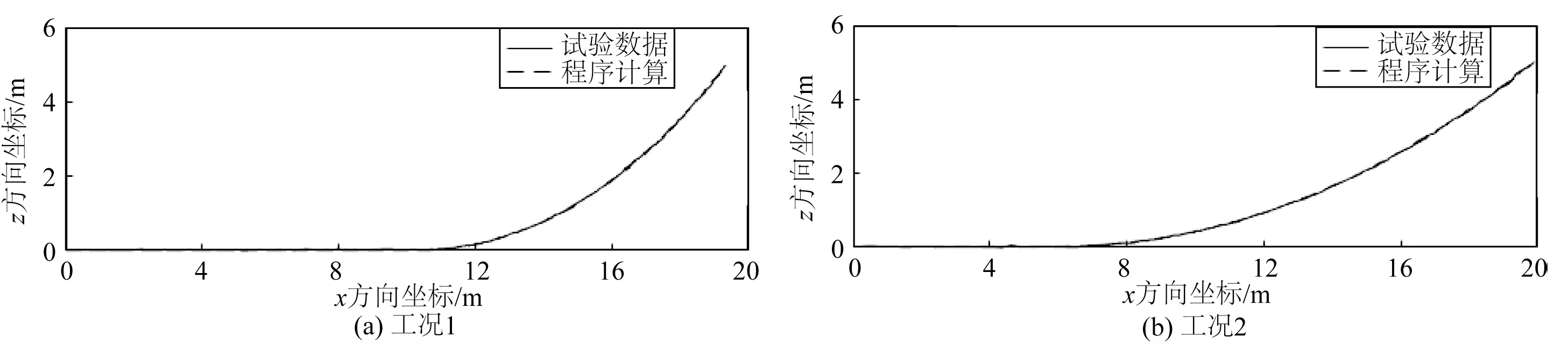
图8 工况1和2的试验和程序计算静态形状比较Fig.8 Comparison of experimental and programmed static shapes for Cases No.1 and 2

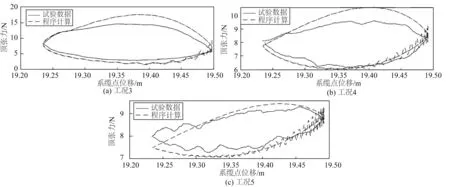
图9 工况3～5试验和程序计算顶张力与系缆点x坐标关系Fig.9 Experimental and procedural calculation of top tension relating to the x coordinate of the fairlead point for Cases No.3～5

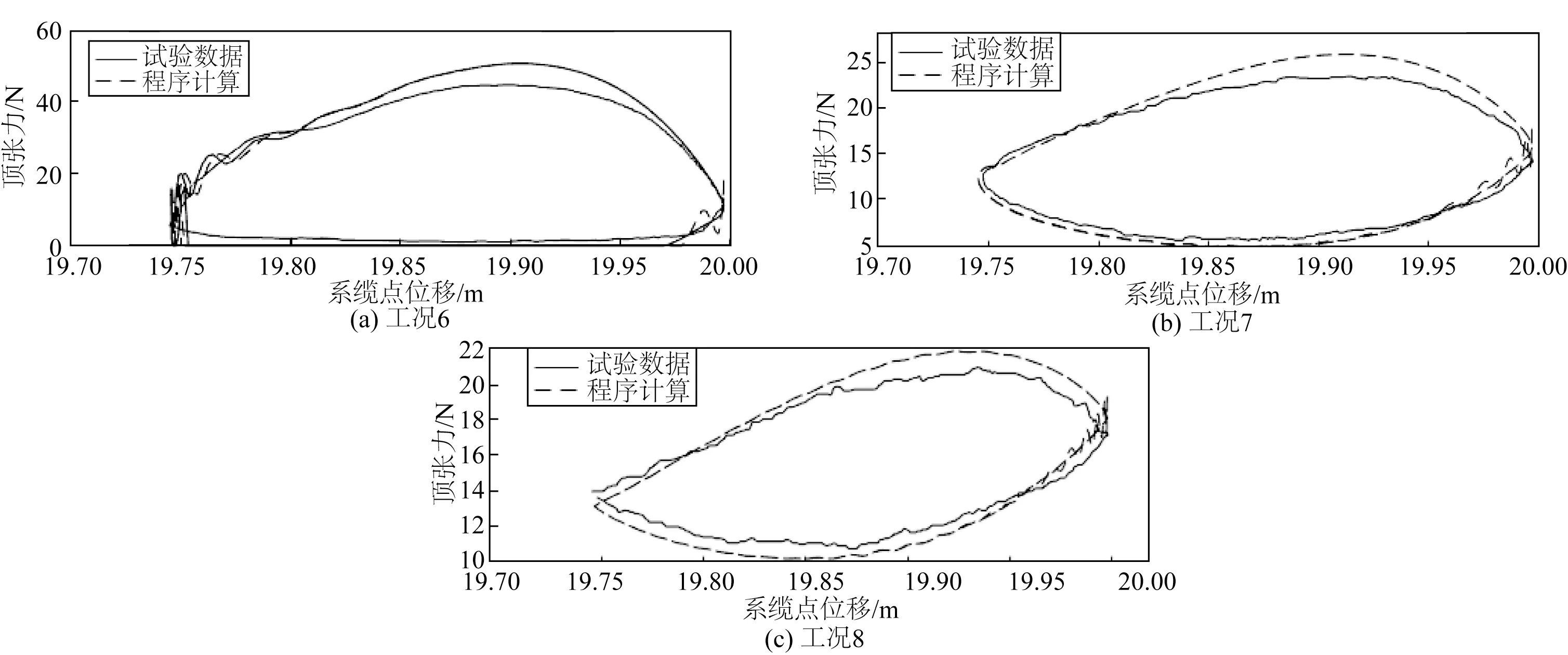
图10 工况6～8试验和程序计算顶张力与系缆点x坐标关系Fig.10 Experimental and procedural calculation of top tension relating to the x coordinate of the fairlead point for Cases No.6～8

表4 静态情况顶张力Tab.4 Top tension of static condition

图8为工况1和2对应的锚链空间形态，实线为试验测量结果，虚线为数值模拟结果，可见两种不同水平跨距工况下数值模型可以很好地模拟锚链的静态空间形态。同时，表4 中对比了两种静态工况下试验与数值计算得到的顶张力，可见两者的误差在3%以内。

图9 和10 为不同水平跨距的配置下各工况顶张力试验与数值计算结果的对比。图9 和10 中横轴和纵轴分别为系缆点位移和对应的顶张力，实线代表试验测量结果，虚线代表程序计算结果。从图9 和10 中可以看出，数值计算得到的各工况下动态张力结果与试验测量结果符合较好。由于数值振荡的存在，数值模拟结果在初始阶段会出现明显的高频振荡，振荡的周期为锚链弦振动固有周期，数值振荡在初始的系泊缆运动周期内会迅速衰减消失，对计算结果无影响。

从图8～10及表4可以看出，对于单根钢链，无论是静态还是动态情况，数值计算结果都与算例结果相差不大，曲线拟合度较高，初步验证了该数值模型可应用于钢锚链的数值模拟中。

2.2 单根锚链模型试验与验证

2.2.1 试验设置

在波流水槽中开展单根钢锚链模型试验并进行数值模型的验证，试验中锚链参数如表5所示。与2.1节算例中系缆点做水平往复运动不同，这里试验中系缆点做圆周运动。如图11、12 所示，系缆点连接在圆盘上，圆盘上的系缆点可设置在不同的半径处，电机可以产生不同的转速，使系缆点产生不同周期和幅值的圆周运动。系缆点上连接测压计用于测量锚链的顶张力。试验工况如表6 所示，设置不同激励半径和电机转速的25个工况进行试验。

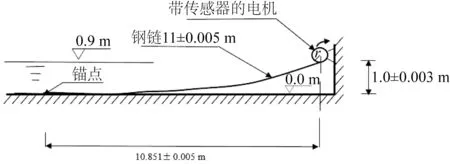
图11 试验布置示意Fig.11 Schematic diagram of the experimental arrangement

图12 试验实物Fig.12 Setup of the experiment

表5 锚链参数Tab.5 Steel chain parameters

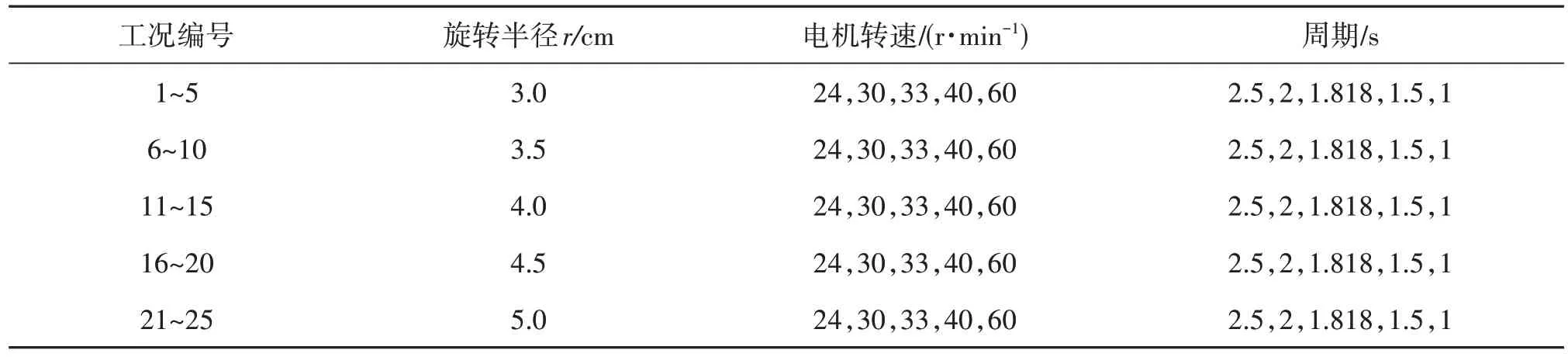
表6 试验工况Tab.6 Experimental cases

2.2.2 试验结果及验证

通过数值模拟得到各工况下顶张力时历曲线和顶张力幅值并与试验结果进行对比，验证数值预报程序的准确性。半径r=3 cm 的对比结果如图13～15所示，r=4 cm 的对比结果如图16～18所示，r=5 cm 的对比结果如图19～21所示。

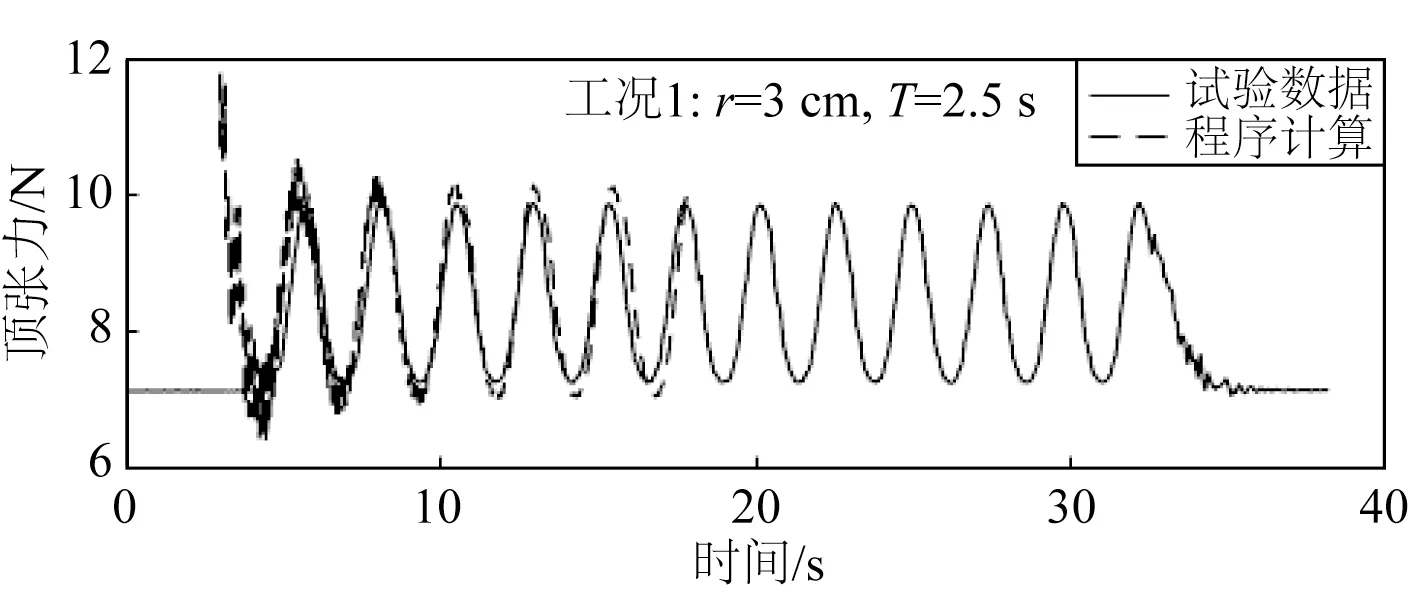
图13 工况1顶张力时历曲线对比Fig.13 Comparison of top tension time histories for case No.1

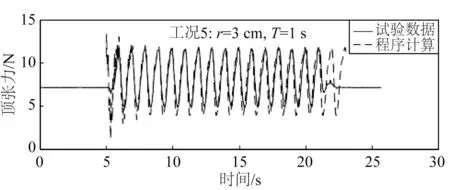
图14 工况5顶张力时历曲线对比Fig.14 Comparison of top tension time histories for case No.5

从图13 和14，图16 和17，图19 和20 可以看出，试验和数值计算的顶张力时历曲线拟合度很高，因此进一步验证了开发的数值模型可应用于全链。当激励周期一定时，旋转半径越大，锚链的顶张力越大，当激励半径一定时，旋转周期越小，顶张力越大。同时，图15、18 和21 显示，当激励半径一定时，旋转周期越小，数值计算得到的顶张力幅值与试验的差异越大。

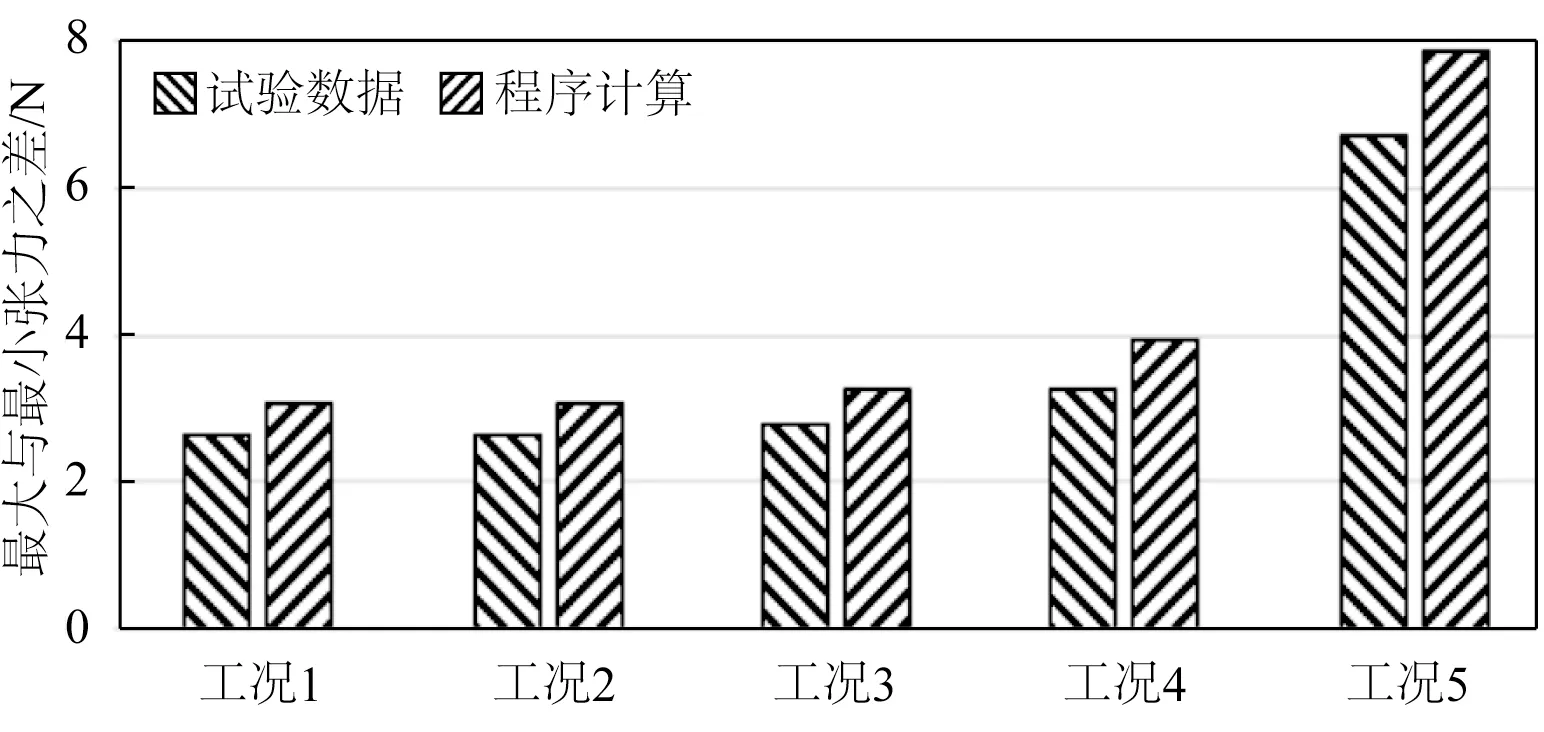
图15 工况1～5顶张力幅值对比Fig.15 Comparison of top tension amplitude for cases No.1～5

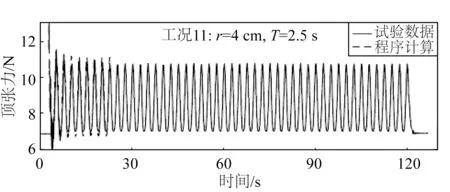
图16 工况11顶张力时历曲线对比Fig.16 Comparison of top tension time histories for case No.11

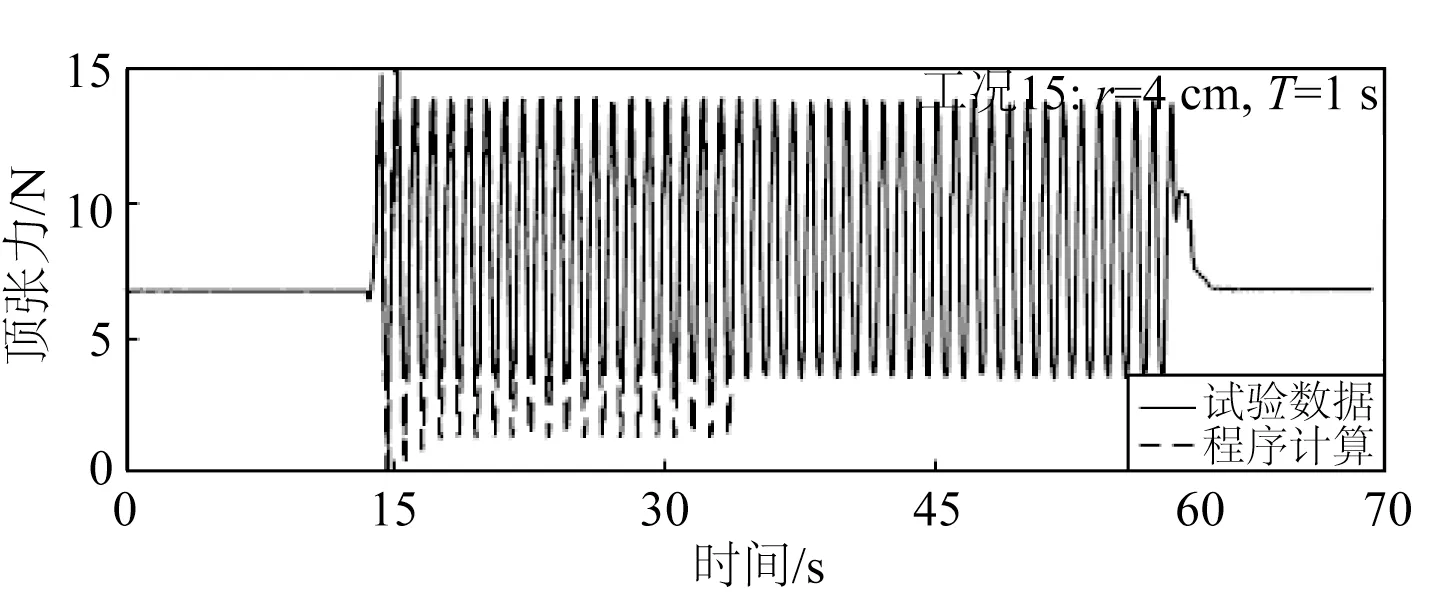
图17 工况15顶张力时历曲线对比Fig.17 Comparison of top tension time histories for case No.15

图18 工况11～15顶张力幅值对比Fig.18 Comparison of top tension amplitude for cases No.11～15

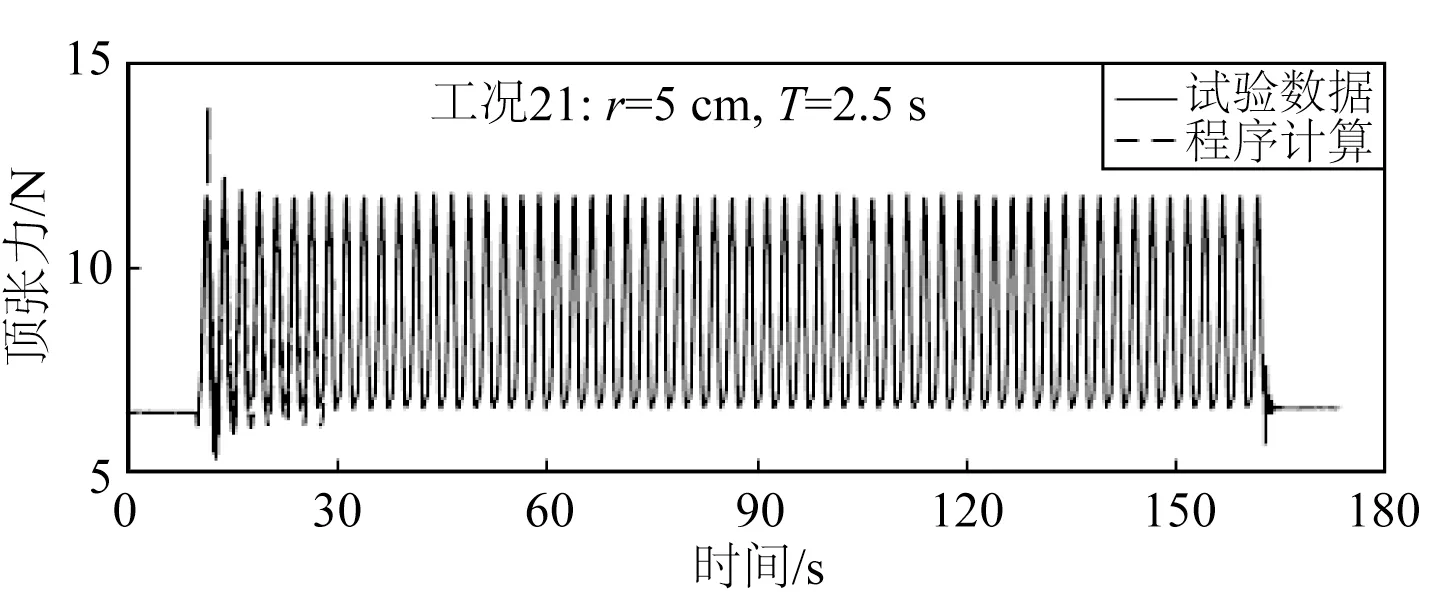
图19 工况21顶张力时历曲线对比Fig.19 Comparison of top tension time histories for case No.21

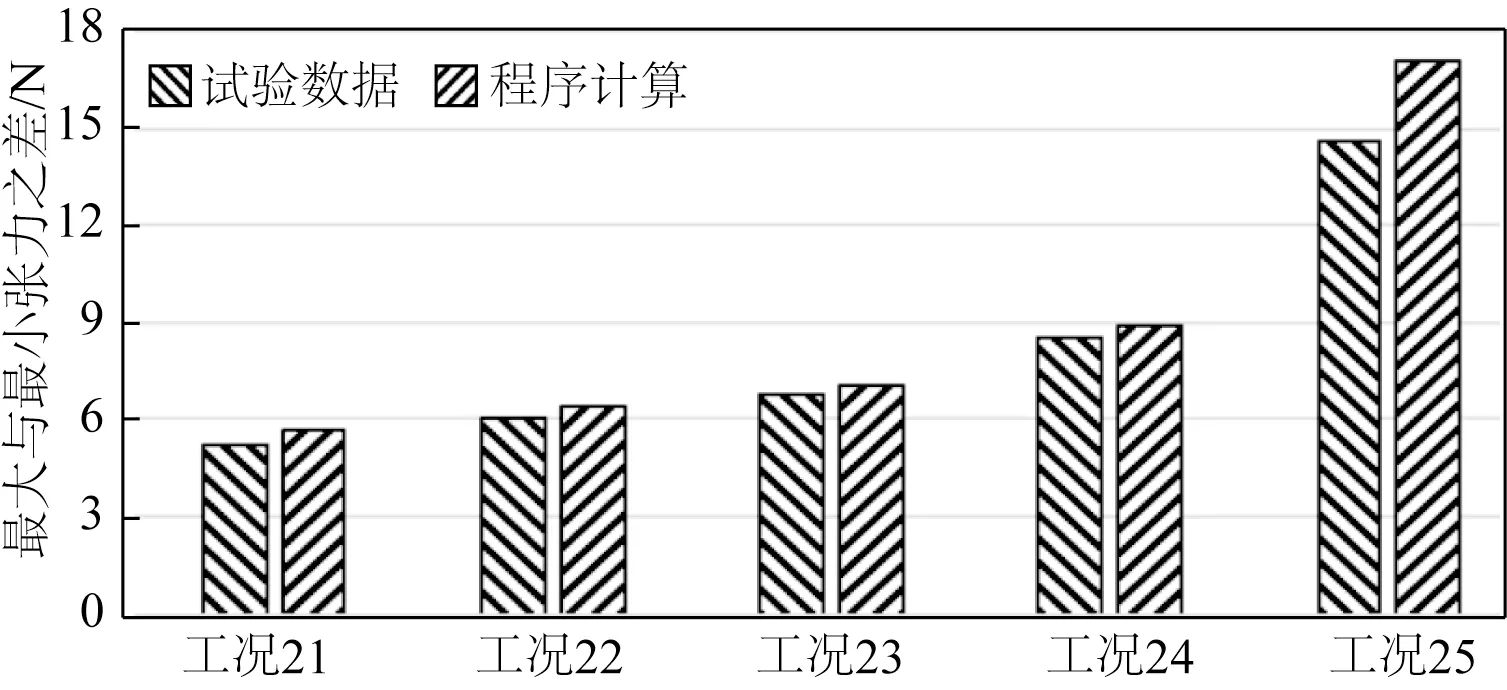
图21 工况21～25顶张力幅值对比Fig.21 Comparison of top tension amplitude for cases No.21～25

此外，与图9 和10 中相似，在图13 和14 的顶张力初始阶段也出现了由数值振荡造成的高频振荡，但在几个周期后这种振荡很快衰减消失。

3 链—缆—链式复合系泊链缆的模拟与验证

依据乔东生和欧进萍［10］提供的算例结果对数值模型在链—缆—链式复合系泊链缆模拟中的准确性进行验证。

3.1 模拟工况

算例中采用链—复合纤维缆—链式复合系泊链缆布置，如图22 所示，其中OA段和BC段为钢链，AB段为由聚酯纤维制成的合成纤维缆，相应参数如表7所示。

图22 试验布置示意Fig.22 Schematic diagram of the experimental arrangement

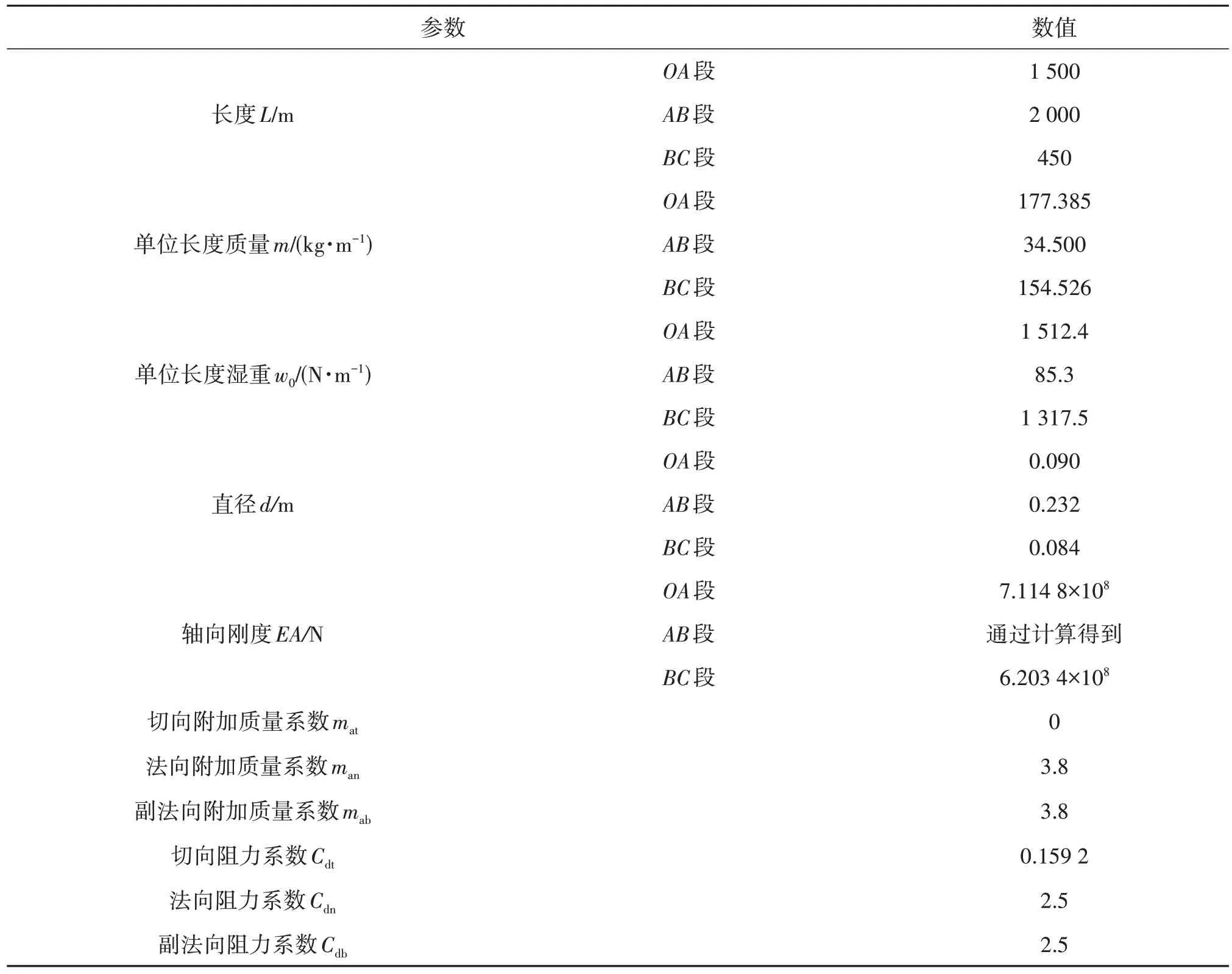
表7 链—缆—链锚泊线材料参数Tab.7 Chain⁃cable⁃chain mooring line material parameters

数值计算中将整段链缆划分为100个等长的杆单元，图22中i的范围代表不同材料链缆的单元号范围，程序依据表7对不同材料的杆单元赋予不同的材料参数。式（18）中的系数为α′= 14.469，β′= 0.211 3和γ′=0.269 7。采用数值模型分别对复合系泊链缆进行静刚度和动刚度迭代，动刚度迭代由波频运动和慢漂运动组成，动刚度下计算工况如表8所示。

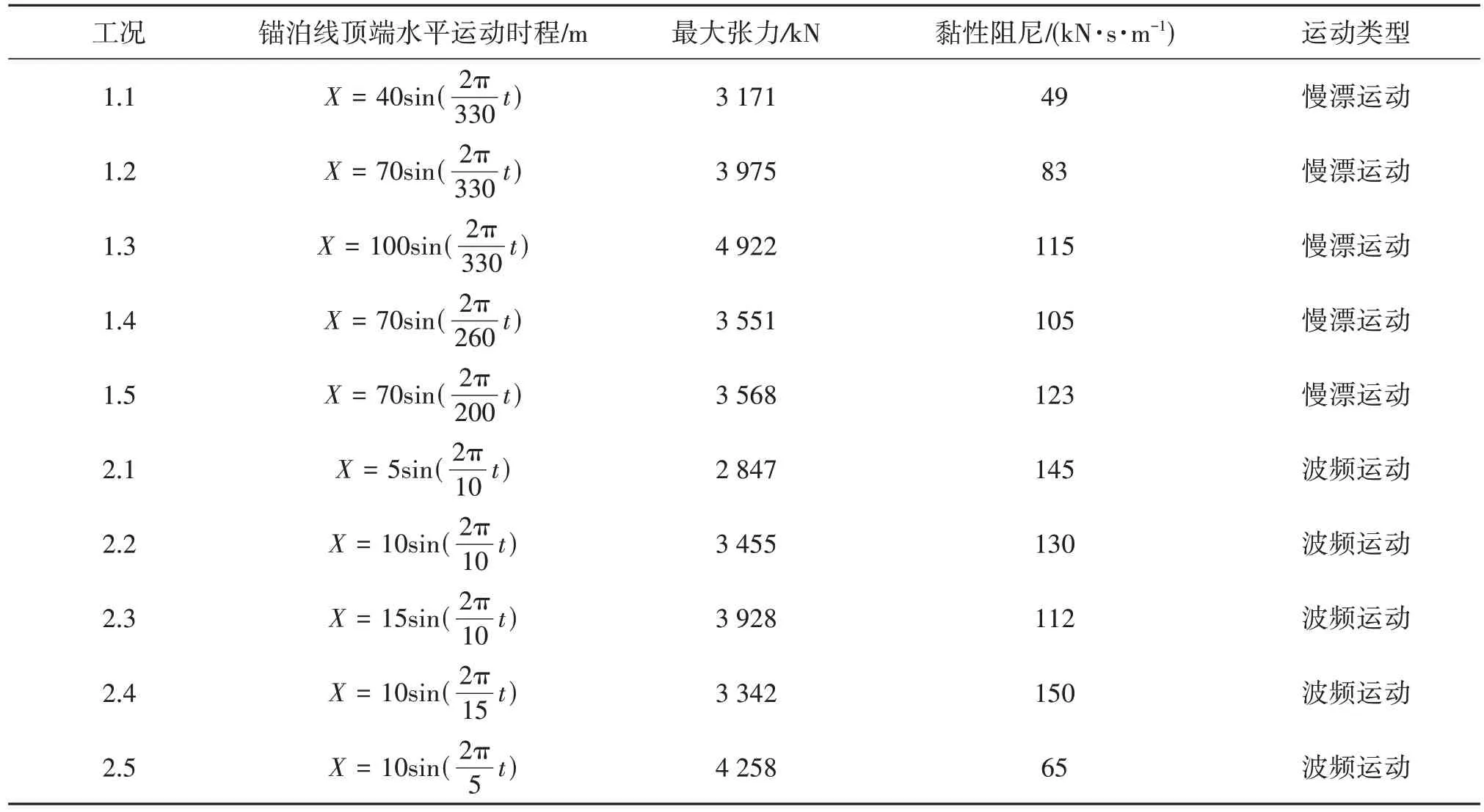
表8 动刚度计算工况Tab.8 Calculation cases

3.2 结果与验证

首先，按照1.2节的流程进行静刚度迭代，其中容差ε设置为106Pa。以T=200 s为一个迭代周期，迭代结果如表9所示，其中0，1和2表示迭代次数，并由式（19）计算文献中算例结果与文中数值模拟结果间的误差δ。

式中：A为链—缆—链式复合系泊链缆的模拟结果，B为参考文献［10］的算例结果。

表9中显示了不同初始顶张力下的静刚度迭代结果。

图23为初始顶端预张力为1 334 kN时，静刚度迭代过程中杨氏模量随时间的迭代曲线。该工况下第一次和第二次的迭代结果分别对应图中（200，16.39）和（400，16.39）两点。从表9可以看出，静刚度数值模拟结果与参考文献［10］中的结果差异较小，最大误差在5%以内，因此该数值模型可用于链—缆—链式复合系泊链缆的静刚度迭代。

图23 杨氏模量随时间的迭代曲线Fig.23 Iteration of Young′s modulus with time

根据1.2 节的流程进行动刚度迭代，各工况下的迭代结果如表10 所示，0～6 表示迭代次数，每个周期迭代一次。误差同样由式（19）计算。对于波频运动，取t=0.01 s为时间步长。La是动张力变化幅值占最大破断张力（MBL）的百分比。动张力变化幅值是通过获得前一周期动张力的最大值和最小值来计算的。对于慢漂运动，选择了合适的时间步长后，La以同样的方法求解。

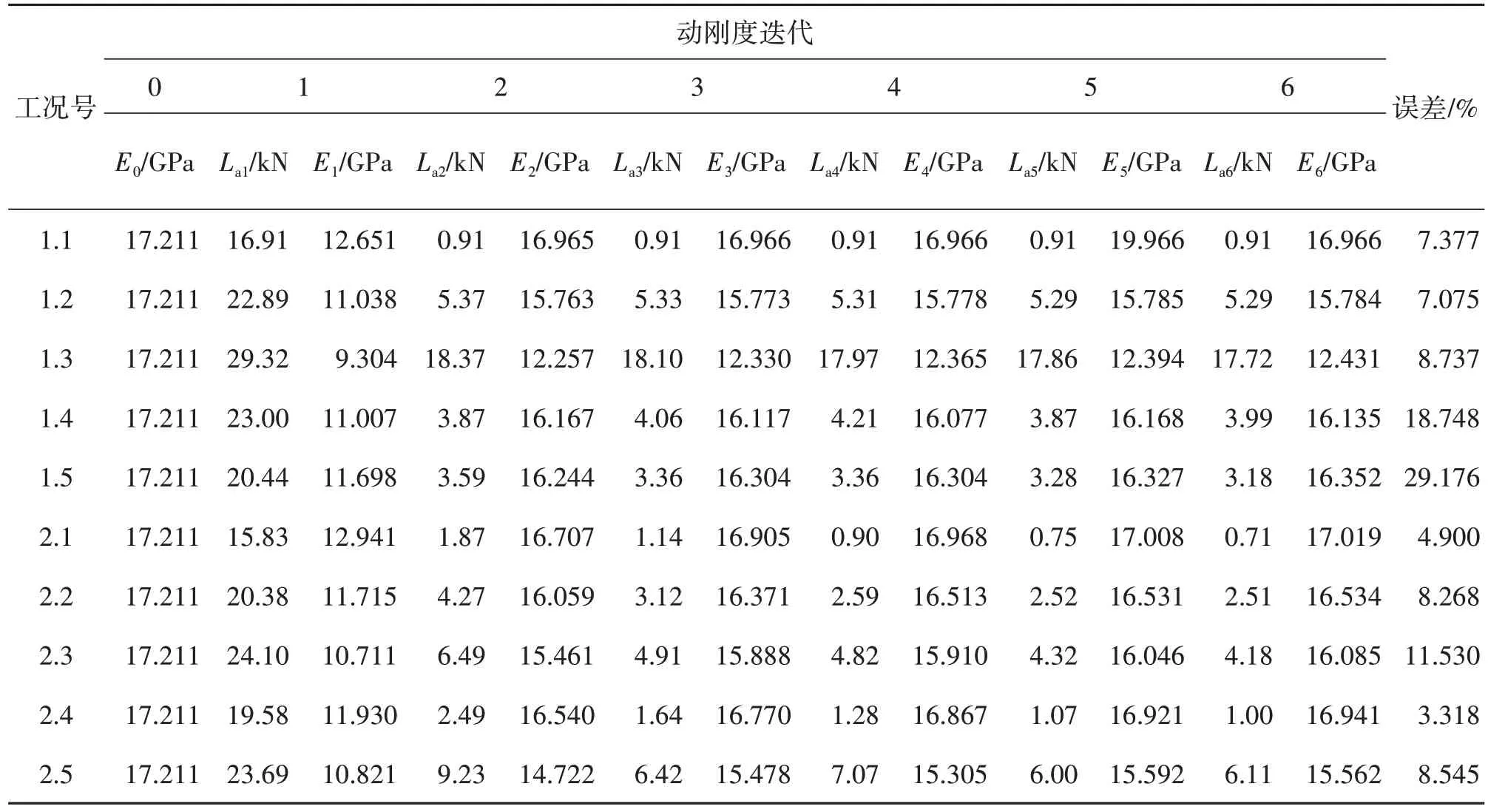
表10 动刚度迭代结果Tab.10 Dynamic stiffness iterative results

图24 和25 分别为工况1.1 中顶张力和轴向刚度的时历曲线。图26 和27 分别展示了工况2.1 中顶张力和轴向刚度的时历曲线。

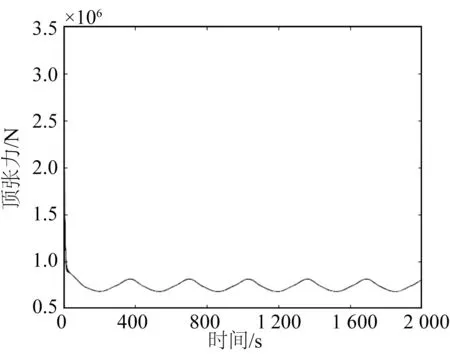
图24 工况1.1顶张力时历曲线Fig.24 Top tension time history for case No.1.1

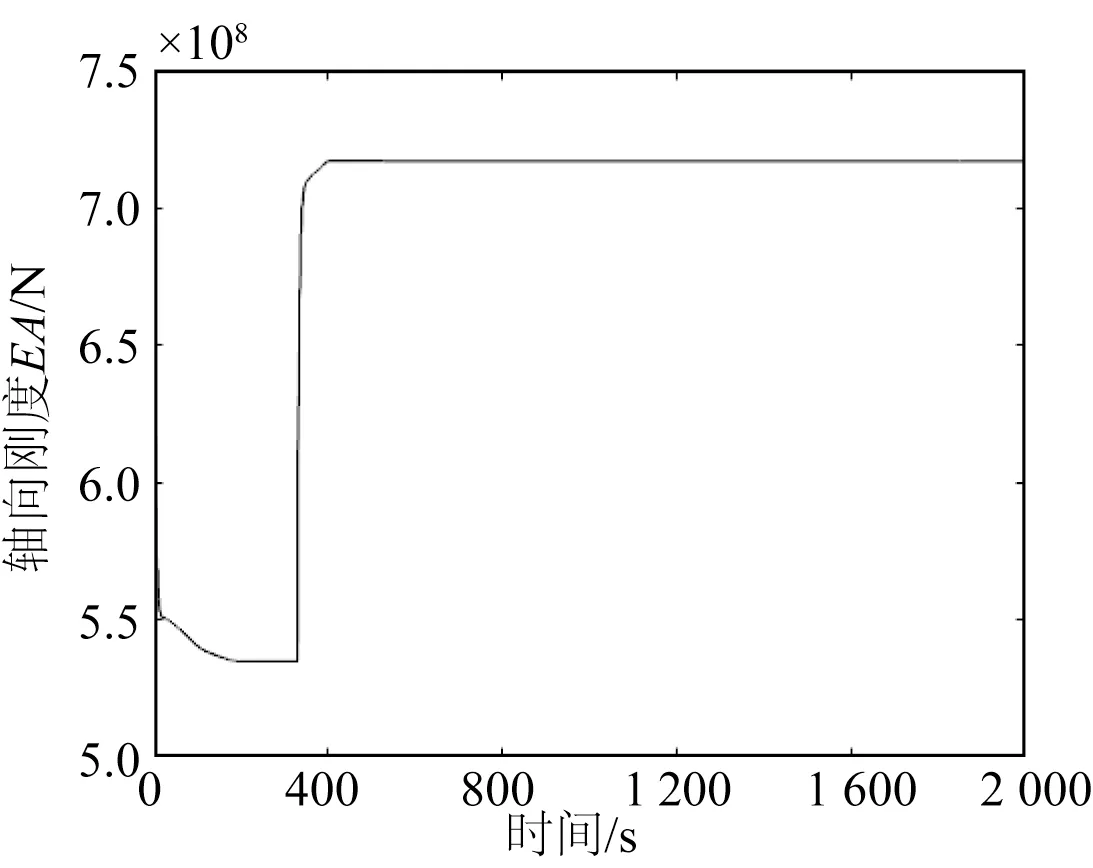
图25 工况1.1轴向刚度迭代曲线Fig.25 Iteration of axial stiffness for case No.1.1

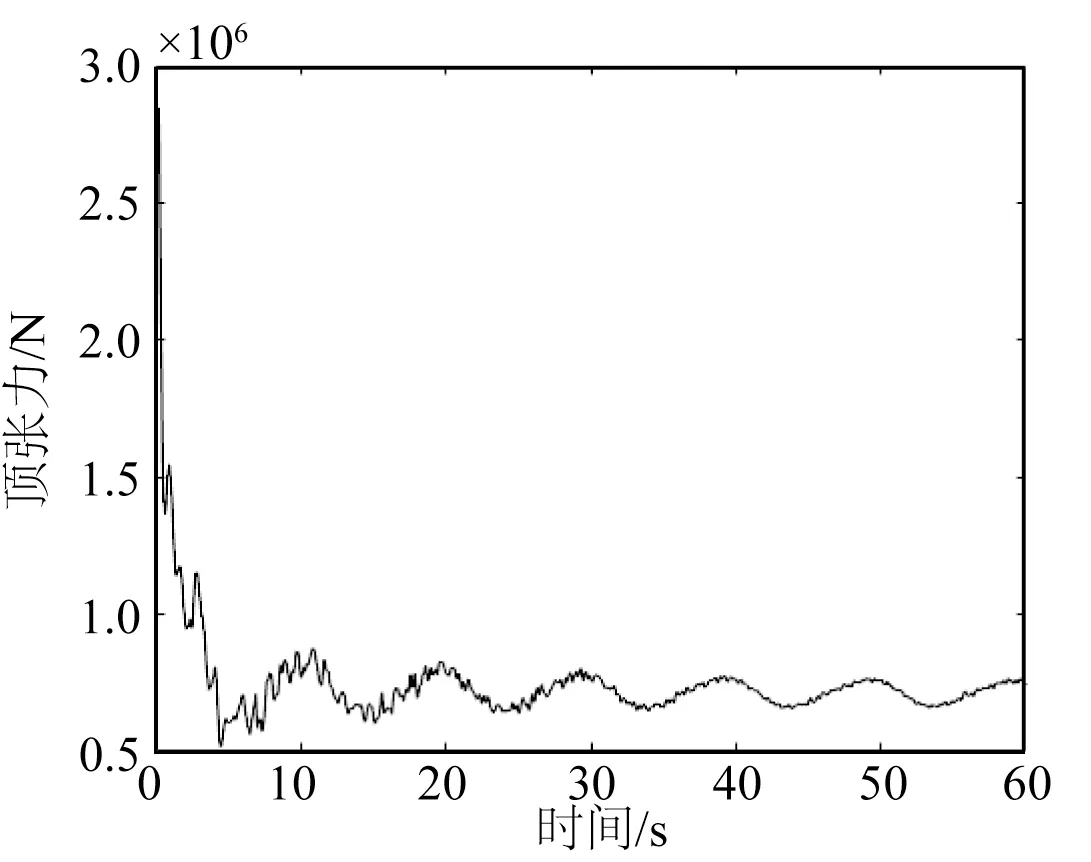
图26 工况2.1顶张力时历曲线Fig.26 Top tension time history for case No.2.1

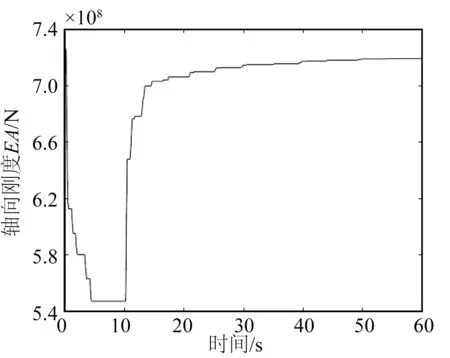
图27 工况2.1轴向刚度迭代曲线Fig.27 Iteration of axial stiffness for case No.2.1

根据表8 和10 可知，对于慢漂运动，在相同的激励周期下，激励半径越大，复合系泊链缆的最大张力越大，轴向刚度越小，动刚度迭代数值计算结果与算例的误差基本保持不变。在相同的激励半径下，激励周期越小，复合系泊链缆的最大张力越大，轴向刚度越小，动刚度迭代数值计算结果与算例的误差增加。对于波频运动，在相同的激励周期下，激励半径越大，复合系泊链缆的最大张力越大，轴向刚度越小，动刚度迭代数值计算结果与算例的误差增大；在相同的激励半径下，其规律与慢漂运动相同。总体上，除工况1.4 和1.5外，动刚度迭代数值计算结果与算例结果的误差在10%以内，这表明该数值模型可用于链—缆—链式复合系泊链缆的动刚度迭代。

由于式（18）中的系数α′、β′和γ′均是与缆绳直径、股数、结构、材料、荷载作用方式等相关的参数。对于聚酯缆，在正弦式载荷的作用下，α′的取值范围为10～23 GPa，参数β′和γ′的取值范围一般分别为0～0.25 GPa和0～0.32 GPa。当系数α′、β′和γ′在取值范围内变化时，静刚度和动刚度的迭代结果也随之变化，当式（18）中系数α′、β′分别取10 GPa 和0.1 GPa 时，静刚度的杨氏模量取得最小值Emin；当式（18）中系数α′、β′分别取20 GPa和0.25 GPa时，静刚度的杨氏模量取得最大值Emax，并由式（19）计算文献中算例结果与本文数值模拟结果间的误差。各工况下杨氏模量最大值和最小值Emax、Emin及其对应误差分别如表11和表12所示。其中，表11 中当弹性模量取得最大值Emax时，系数α′、β′分别增大了38.23%和18.32%，引起误差最高达到了41.72%，当弹性模量取得最小值Emin时，系数α′、β′分别增大了30.89%和52.67%，引起误差最高达到了35.42%。表12 中当弹性模量取得最大值Emax时，系数α′、β′分别增大了38.23%和18.32%，系数γ′减小了62.92%，引起误差最高达到了55.48%，当弹性模量取得最小值Emin时，系数α′、β′分别减小了30.89%和52.67%，系数γ′增大了18.65%，引起误差最高达到了68.22%。因此，在对复合系泊链缆进行刚度迭代计算时，要准确选取相应的参数α′、β′和γ′，尽量减小计算误差。

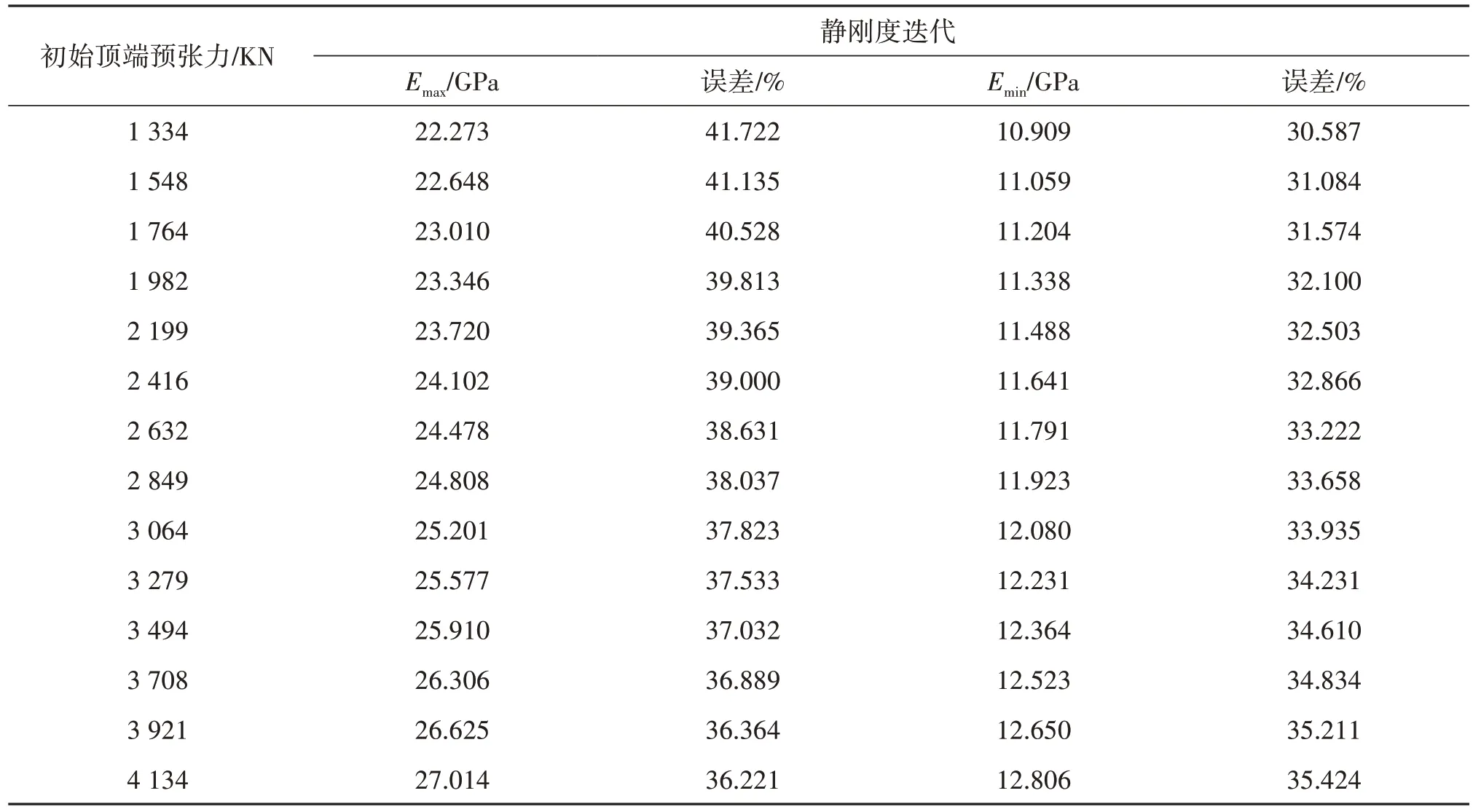
表11 静刚度经验公式系数影响Tab.11 The influence of coefficient in empirical formulas for static stiffness

表12 动刚度经验公式系数影响Tab.12 The influence of coefficient in empirical formulas for dynamic stiffness

4 结 语

建立了基于有限差分法的复合系泊链缆动力模型。文中使用已有算例和模型试验对钢链的顶张力进行了模拟，并使用已有算例对链—缆—链式复合系泊链缆的顶张力和刚度进行了模拟。得出以下结论：

1）单根锚链算例和模型试验验证了数值模拟全钢链的准确性。钢链顶张力的大小与激励半径和激励周期有关，当激励半径一定时，激励周期越小，顶张力及其幅值变化越大，钢链运动就越剧烈；当激励周期一定时，激励半径越小，顶张力及其幅值变化越小，钢链运动就越平稳。

2）通过对链—缆—链式复合系泊链缆的验证，表明该数值模型可应用于复合系泊链缆。对于静刚度迭代，数值模拟结果与算例结果差异较小。对于动刚度迭代，除个别大幅慢漂工况外，两者也有较好的吻合。且当激励半径一定时，激励周期越小，复合系泊链缆顶张力越大，相同周期内La和Lm越大，轴向刚度越小，运动越剧烈；当激励周期一定时，激励半径越小，复合系泊链缆顶张力越小，相同周期内La和Lm越小，轴向刚度越大，运动越平稳。