线驱动自主巡游机器人设计及试验研究

陈祖钢，田新亮，陈 兴，温斌荣，李 欣

（1.上海交通大学 海洋工程国家重点实验室，上海 200240；2.上海交通大学 崖州湾深海科技研究院，海南 三亚 572000）

海洋资源是地球资源的重要组成部分，在开发利用海洋资源的过程中，水下机器人起到了无可替代的作用，如自主无人航行器（AUV）。传统的AUV具有控制简单、可靠性高、航行续航时间长等优点，然而，与鱼类和海豚等水生动物相比，其存在效率低、机动性差、噪声高等缺点［1］，因此，研究人员和工程师转向研究性能更优异的水下机器人。经过数年的发展，以仿生机器鱼为代表的新型水下机器人成为研究的热点。Breder［2］根据鱼的运动形态差异，将鱼分为身体/尾鳍（body and/or caudal fin，简称BCF）推进模式和中央鳍/对鳍（median and/or paired fin，简称MPF）推进模式，其中BCF模式具有推进速度快、推进效率高等优点，自然界中85%的鱼类均采用该种推进模式［3］，如鲤鱼、金枪鱼等；由于BCF 模式的优点，具备BCF 推进模式的鱼类也是研究人员进行仿生机器鱼研制时研究的重点。

仿生尾鳍是机器鱼实现仿生游动的重要部分，针对仿生尾鳍机械设计的不同，可大体分为刚性驱动及柔性驱动，如多关节舵机、形状记忆合金（SMA）、离子交换聚合金属材料（IPMC）等；以此为基础，科研人员研制了多种机器鱼样机。1994 年，Triantafyllou 和Triantafyllou［4］以金枪鱼为仿生对象，研制出了世界上第一台真正意义的仿生机器鱼RoboTuna；Liu和Hu［5］以鲹科鱼类为仿生对象，提出了一种三关节舵机驱动的仿生机器鱼，通过搭载惯性测量单元（IMU）等传感器，该机器鱼可实现自主游动；Zhu等［6］研制了一种单舵机驱动的机器鱼，其尾鳍由柔性蒙皮及被动末端关节构成，由于关节数较少，该机器鱼可实现最高15 Hz的高频摆动，直线游动速度可达1.02 m/s；Katzschmann等［7］提出了一种循环液泵驱动的柔性机器鱼，该机器鱼可实现水下声学遥控，并能通过改变胸鳍攻角实现沉浮运动；Rossi等［8］提出一种可模仿鱼类肌肉运动的机器鱼，该机器鱼以SMA为驱动材料，通过控制SMA的收紧及松弛从而实现尾鳍连续的弯曲摆尾等动作。

文中研制了一种拉线驱动的仿生机器鱼“逍遥”，该机器鱼以拉线结构驱动的柔性尾鳍作为主要推进器，通过舵机及拉线直接控制尾鳍的运动，通过搭载IMU 等传感器，机器鱼“逍遥”可具备自主游动能力；同时，对机器鱼“逍遥”开展了开敞水池试验，记录分析了直行游动速度、转向游动速度、角度调节时间等试验数据，并通过改变尾鳍摆尾角度控制信号输入，对比分析了摆尾幅度及摆动频率对游动性能的影响，综合评估了其游动性能。

1 鱼类运动学及设计原理

在BCF 运动中，鱼的摆尾运动主要集中在身体后1/3，基于对鱼类运动形态的观察，鱼类研究学者Lighthill将此类摆尾运动以一组行波方程来描述，即鱼体波函数［9］：

式中：y(x，t)为鱼体偏移身体轴线的侧向位移；x为鱼体体长；c1和c2分别为一次波幅包络系数及二次波幅包络系数；k和λ分别为鱼体波波数及波长；ω= 2πf为鱼体波的角频率，f为鱼尾拍动频率。

文中设计的机器鱼选取c1=0.15，c2=0.20，k=1.2 作为设计参数，其中鱼身总长L=900 mm，设摆动周期为T，则其理想摆动形态如图1所示。

2 仿生机器鱼结构设计

2.1 机械设计

如图2 所示，机器鱼“逍遥”由刚性头部、胸鳍及柔性鱼尾组成，内部器件参数规格如表1 所示。胸鳍由刚性鳍板通过舵臂与两台30 kg·cm、7.4 V 防水舵机直连驱动，通过不对称的摆动实现沉浮运动。刚性头部采用树脂材料3D 打印制造，其形状为流线型从而减少流体阻力，同时为水密舱、配重舱及胸鳍提供了放置空间。考虑到机器鱼的体积较大，采用整体防水方式较为困难，因此单独设置了水密舱以放置电控模块，并且在舱外预留了水密插头，从而实现在不拆卸水密结构的前提下进行机器鱼的充电、程序烧录等操作。

表1 “逍遥”机器鱼规格Tab.1 Specification of “XiaoYao”robotic fish

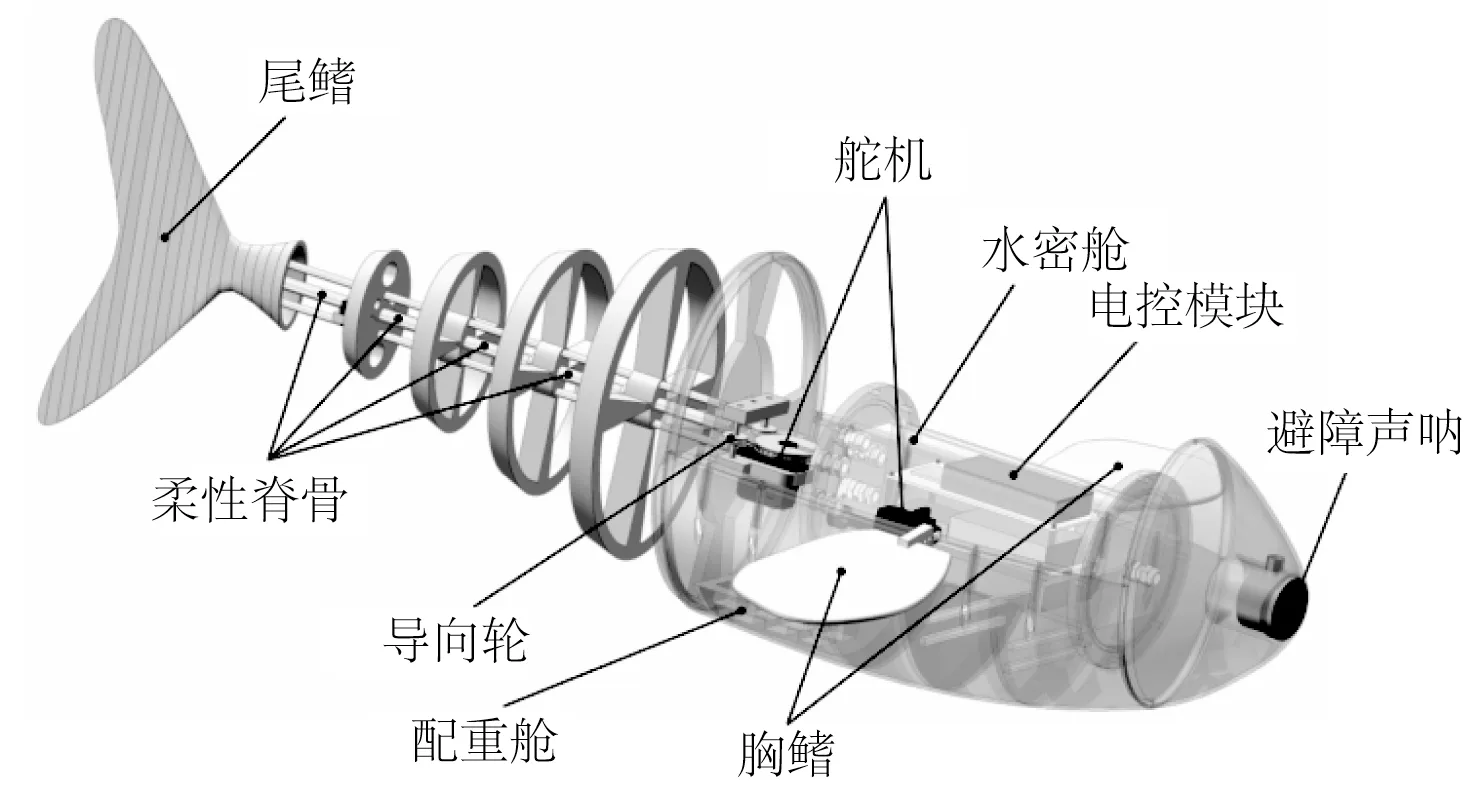
图2 仿生机器鱼结构Fig.2 Mechanical configuration of biomimetic robotic fish

柔性鱼尾由拉线机构、柔性脊骨及末端尾鳍构成，柔性脊骨包括了中央一根较粗的弹性梁和一对较细的弹性梁，均为聚氨酯材料制作，具有较好的回弹性及耐老化性；相比于仅采用单根弹性梁作为鱼尾脊骨，这种设计可防止鱼尾在摆动过程中发生轴向滚动，干扰尾鳍的击水动作。拉线机构由一台50 kg·cm、7.4 V的防水舵机、拉线绳、导向轮及末端锚点构成，考虑到舵机拉力较大且需要往复运动，容易造成拉线的磨损及老化，经过横向对比，最终采用了抗拉力高、耐腐蚀的芳纶线。拉线的一端绕过安装在舵机上方的绕线轮，另外两端固定在鱼尾末端关节。当舵机往复旋转时，通过牵拉两端拉线直接驱动鱼尾关节，从而实现鱼尾的连续摆动。因为尾鳍部分没有受到拉线的直接牵引而是由弹性脊骨连接，在摆尾过程中尾鳍受到水流阻力时可带动弹性脊骨弹性弯曲，产生相位滞后的摆动，从而自然产生“S”型鱼尾波动，该摆尾动作相比于“C”型摆动能够获得更好的推进效果［10］；此外，相比于传统的多关节舵机鱼尾设计，该种拉线式机构还具有结构简单、机械损耗小、能量传递效率高等优点［11］。

2.2 电路设计

机器鱼“逍遥”的电控系统采用了分层架构形式，具体包括上位机Raspberry Pi 4B、下位机STM32单片机及IMU 等传感器构成，系统框图如图3 所示。Raspberry Pi 4B 作为数据处理器，其功能在于接收传感器返回的数据，经过算法处理后通过串口向STM32 单片机发送控制指令，STM32 作为脉宽调制（PWM）信号发生器驱动舵机动作。机器鱼中的传感器主要包括IMU、压力传感器和声呐。IMU（JY901B）可以获取仿生机器鱼的姿态、航向、三维位置和速度信息，压力传感器（MS5837）通过检测环境压力来计算所在深度，声呐（P30）通过探测正面环境来返回障碍物信息，实现避障动作。机器鱼可通过无线模块（ESP01S）完成与地面计算机的数据交互及在线编程，有效避免了对水密舱的频繁开闭。采用分层架构能够提高传感器的搭载能力，可将控制算法及底层驱动算法进行分别模块化处理，减小单机计算负荷，便于后期算法的更新及维护。

图3 仿生机器鱼组成原理Fig.3 Function of biomimetic robotic fish

2.3 控制算法设计

为了模拟真实鱼类摆尾运动，机器鱼“逍遥”采用了改进的中枢模式发生器（central pattern generator，简称CPG）算法作为PWM 波发生器以控制尾鳍舵机［12］，通过设置幅值、频率、偏置及周期比率4个参数，CPG能够生成任意可模拟节律运动的正弦波形，其基本方程为：

式中：B为偏置量输入；M为幅值输入；ω为角频率输入量；R为时间比率；b为偏置状态量；m为幅值状态量；ϕ为相位状态量；kb为偏置量增益系数；km为幅值增益系数；α为波形输出量。

为了获取CPG 控制参数与实际尾鳍末端最大摆动角的几何关系，开展摆尾运动学辨识试验。试验中将机器鱼尾单独固定，并在鱼尾正上方架设高速摄影机，通过无线模块发送不同的CPG 参数控制鱼尾低频摆动，利用高速摄影机完成拍摄。通过后期分帧图像处理，最终得到CPG 幅值参数与真实鱼尾最大摆动角的关系。为了消除水流阻力对试验结果的影响，试验选择在空气中进行；根据试验测量结果，可确定不同的幅值参数M对应的实际尾鳍末端单侧最大摆动角，如表2所示。

表2 CPG幅值参数与鱼尾单侧摆动角关系Tab.2 Relationship of CPG amplitude parameter and single side bending angle of robotic fish tail

机器鱼“逍遥”还采用了PID 控制器实现航向角控制。在机器鱼游动过程中，机器鱼的航向角将由IMU实时采集，将实际航行角与预定的航向角之差作为PID控制器输入，并将PID控制器的实时输出值作为后续CPG 算法的偏置量输入值，最终由CPG 生成PWM 波控制舵机以特定角度范围运动，完成航向角的闭环控制。基本方程为：

式中：θ为实际航向角；θ*为期望航向角；B(t)为CPG 的偏置量输入；Kp、Ki及Kd分别为PID 控制器的比例、积分、微分增益系数。

经过参数优化试验并选取控制效果最佳的参数组合，文中采用的PID参数分别为0.5、0.15及0.05。

3 试验结果及分析

在敞开水池开展试验，综合评估机器鱼“逍遥”的游动性能。试验所使用的机器鱼“逍遥”实物如图4 所示。试验过程中上位机将通过无线模块与机器鱼上的微控制器进行实时通讯，对机器鱼进行预先编程后由机器鱼自主决策完成预定任务，如直行、稳定转向及目标角度转向等。试验在尺寸为20 m×15 m ×1.8 m（长×宽×高）的空旷水池进行，游动耗时的采集是通过人工计时及后期视频分帧处理统计时间来完成的，每项试验均进行5 次重复测量，最终取平均值作为测量结果。试验的目的在于测试机器鱼游动性能，即直行、稳定转向、目标角度转向等任务场景下的游动速度及响应时间，综合评估机器鱼的游动性能。

图4 仿生机器鱼实物Fig.4 Actual picture of robotic fish

3.1 直行试验

通过设定不同尾鳍期望摆角幅度及摆动频率，测得机器鱼“逍遥”多组前行试验数据，数据结果如图5所示。

图5 前行游动试验结果Fig.5 Forward swimming experiment result

试验中测得的最大游动速度为0.138 m/s，即0.153 BL/s；最小游动速度为0.040 m/s，即0.044 BL/s。随着摆动频率的升高，其游动速度呈现二次函数形式，当摆动频率较高时，其游动速度明显下降。以期望摆动角45°为例，当摆动频率为0.45 Hz时，对应的直行速度为138.3 mm/s；而当摆动频率提升至1.05 Hz时，直行速度下降至84.9 mm/s，下降幅度为38.6%。这是由于当仿生机器鱼的摆尾频率逐渐上升时，由于驱动舵机最大转矩的限制及高频摆动下流体阻力的增大，其尾鳍摆动角幅度通常无法达到CPG 产生的期望最大摆幅，如0.45 Hz 下测得摆动幅度为45°，在1.05 Hz 时仅为13°，摆动幅度的下降造成有效前进推力的下降，从而导致游动速度的下降。

与之相反的是，自然界的鱼类往往通过提高摆动频率来提高游动速度，其游动速度与摆动频率大致呈线性正相关［13］；这是由于真实鱼类在游动频率逐渐增大的同时能够通过调节自身尾部肌肉刚度变化，使其仍能保持较大的摆动幅度，从而维持较高的游动性能。然而仿生机器鱼通常无法根据摆动频率自适应地调节自身鱼尾刚度，其机械系统整体固有频率是基本不变的；当摆尾频率偏离自身固有频率较远时，由于非共振状态导致的摆幅衰减现象会逐渐显著，同样造成高摆频时游动性能的下降［14］。

3.2 转向试验

试验主要考察不同控制参数下鱼尾的转向性能，通过机器鱼稳定绕圈进行数据的采集，试验中鱼尾均单侧摆动，即仅在鱼体中轴线与单侧最大摆尾角之间进行摆动，试验中CPG 的时间比率参数R均设为1；试验结果如图6 所示。试验中测得的最大转向速度为0.123 m/s，即0.136 BL/s；最小转向速度为0.056 m/s，即0.062 BL/s；最大转向角速度为0.113 rad/s，即6.48 （°）/s；最小转向角速度为0.042 rad/s，即2.41 （°）/s。随着摆尾频率上升，转向速度数据呈现出与前行速度数据类似的二次函数形态，反映出前文提及的摆幅衰减现象对其转向速度产生了相似的影响。与之相反的是，转向角速度数据更多的呈现出单调下降趋势。

图6 转向游动试验结果Fig.6 Turning swimming experiment result

根据3.1 节直行试验结论的分析，当摆动频率与自然频率接近时，机器鱼摆尾运动产生的推力最大，游动性能最佳，直行游动速度最快。然而由于转弯运动的特殊性，最大的摆尾推力并不意味着每个转弯周期产生的净转向角最大，这一现象反映在转向角速度随摆频上升大致呈现单调下降现象。对于下降趋势较为明显的期望摆动角为45°、40°及25°的试验组，当摆动频率为0.45 Hz 时，三者对应的转向角分别速度为0.113、0.105 及0.061 rad/s；当摆动频率为0.60 Hz 时，从3.1 节分析可知此时尾鳍摆动产生的推力接近最大值，其对应的转向角速度为0.102、0.095 及0.058 rad/s，分别下降了9.7%、9.5%及4.9%。虽然在期望摆动角35°及30°的组中，0.60 Hz 对应转向角速度相比0.45 Hz 分别有3.0%及3.5%的提升，但是在同样对比方式下转向速度平均有12.9%的提升，直行速度有9.8%的提升，可见转向角速度的提升仍较小。说明在转向的场景下，推力的增大使得单个周期的净转向角提升并不明显，甚至不升反降。

随着摆动频率继续增加并远离自然频率，此时转向角速度继续下降主要是由于转向力变小的原因；由于频率的继续提升导致机器鱼尾鳍最大摆幅开始下降，造成净转向力的下降，最终导致转向角速度的下降。机器鱼在转向过程中尾鳍的不平衡摆动除了带动机器鱼转向外，还产生轴向的推力使得机器鱼前进。与转向角速度的数据趋势不同，转向速度与转向走过的路径长度及耗时直接相关，该路径长度除了受每轮转向的净转向角影响，还跟转向产生的前向速度有关，因此转向速度受复位力的影响较小，其数据特征呈现出与前行速度相似的形式。

3.3 目标角度转向试验

试验目的在于给机器鱼设定相同的初始艏向角及不同期望艏向角度，观察并统计在PID-CPG 控制器控制下机器鱼达到目标角度所需游动时间，以及摆尾控制参数的改变对该时间的影响。图7 展示了试验中机器鱼游动过程的序列，此次试验选取的目标角度值为30°、60°以及90°，考虑到实际游动中产生的机器鱼摇艏导致的角度波动情况，将统计的游动时间取为机器鱼从初始角度出发，直到一个摆尾周期内平均艏向角与目标角度值相差2°所需游动时间。

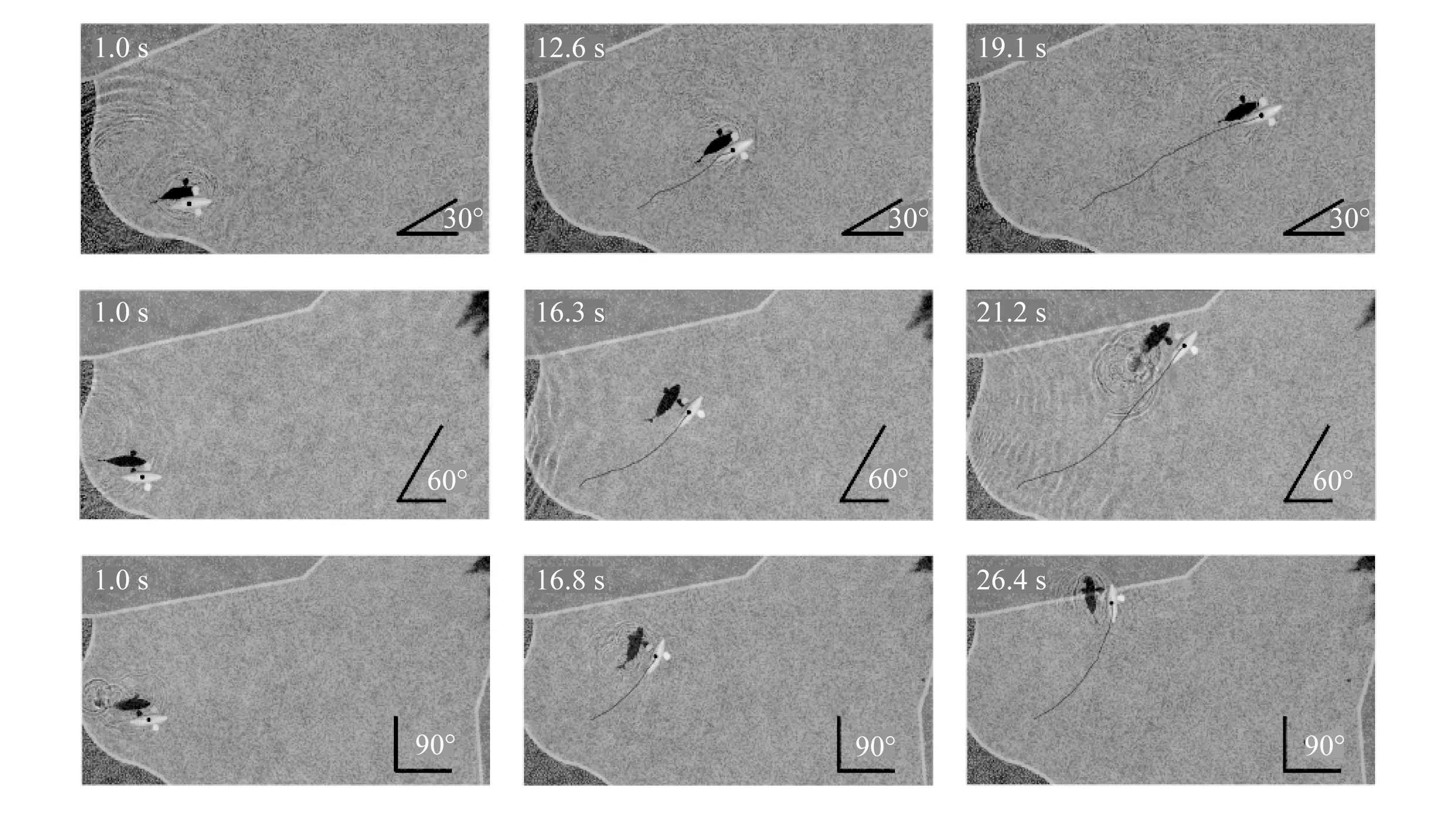
图7 目标角度转向试验序列Fig.7 Sequence of target orientation turning experiment

机器鱼需要从初始艏向角逐渐转向至目标角度，在游动初期由于二者差异较大，PID-CPG控制器输出的摆尾偏移量也较大，因此前期艏向角变化较大；后期随着机器鱼艏向角逐渐达到期望角度，角度变化进入平台调节期，因此艏向角变化较小。试验结果如图8 所示，目标角度为30°、60°及90°时，试验测得最短调节时间分别为17.7、20.9、27.4 s；最长调节时间分别为50.9、62.8、58.9 s。对于相同的目标艏向角及相同的尾鳍摆角控制参数，随着摆动频率的增加，游动时间呈现先下降后上升的趋势，这是由于前文提及的游动性能衰减现象造成游动速度先升后降的结果。

值得注意的是随着设定的期望角度增大，游动时间数据的分层现象逐渐明显，数据一致性增强。这是由于在目标艏向角度较小时，转向过程容易受到机器鱼摇艏现象的影响，造成角度超调；对于摆尾幅度较大的试验组，虽然在转向的初期能够产生较大的转向力，使得机器鱼艏向角快速逼近目标角度，但是尾鳍大摆幅摆动时会增强机器鱼的艏摇现象［15］，造成艏向角的波动，影响了后半段平均艏向角最终稳定至目标角度的过程，造成整体调节时间的延长，甚至高于小摆幅的调节时间。例如目标艏向角度为30°，摆动频率为0.75 Hz 时，摆幅为35°及40°的调节时间分别为22.8 s 及24.6 s；当摆尾角度为40°时，摆动频率为0.60 Hz 及0.90 Hz对应的调节时间分别为25.1 s及24.7 s。因此较小的目标艏向角度容易受到机器鱼摇艏现象的影响，造成调节时间数据的波动。而当期望角度逐渐增大，机器鱼游动所需转向角度增大，游动时间上升，艏向摆动现象对转向过程的影响被削弱，数据一致性及分层现象得到增强，更有助于体现不同的摆尾控制参数对游动时间的影响。

4 结 语

介绍了一种线驱动自主巡游机器人，对其直行、转向及期望角度游动性能进行了试验研究。研究结果表明，特定摆尾角度下机器鱼存在最佳摆尾频率。当摆尾频率接近机器鱼的最佳摆尾频率时其摆尾角度较大，直行及转向的游动速度最快；当摆尾频率较高时，由于机器鱼机械系统舵机最大扭矩限制、流体阻尼的增大及与自身机械共振频率差异等原因，尾鳍摆尾幅度无法达到最大期望值，造成有效推力的下降，最终导致游动速度减小。在目标角度转向试验中，当设定的目标艏向角度较小时，机器鱼的角度调节时间较短，但是调节时间的数据一致性较差；随着目标艏向角度逐渐增大，数据一致性逐渐增强，摆尾参数的变化对游动时间的影响差异逐渐明显。考虑到机器鱼实际游动中涉及到复杂的三维流场问题，未来将对机器鱼多自由度下的动力学建模及游动性能进行研究。