柔性管卷管式铺管上卷有限元模拟

阮伟东，亓可夫，陈苗依，刘 凯，聂庆林

（浙江工业大学 土木工程学院，浙江 杭州 310023）

近年来，随着“加快建设海洋强国”［1］的提出，深海装备的制造能力和技术实力不断提升，“海洋石油981”和“海洋石油286”等大国重器助力海洋油气资源开发与利用走向深蓝。海洋管道作为水下生产系统中最为复杂和重要的组成部分，是目前最高效经济的运输方式，被誉为海上油气田的“生命线”。目前海洋管道铺设方法主要包括：S 型铺管法、J 型铺管法、卷管铺管法和拖曳铺管法。卷管法铺管上卷过程（图1［2］）主要涉及以下设备：吊机、卷筒、半圆塔轮、导向弧板、下水桥、甲板辅助绞车、工作台以及传递工作台。上卷作业一般在岸边船坞完成，管道通过张紧器、校准器和导向弧板螺旋缠绕于卷筒上进行储存。相对于其他铺设方法，卷管铺管法具有铺设速度快、铺管效率高、工程成本低、操作难度小以及可靠性好等优点，广泛应用于海洋油气管道铺设工程。卷管铺管法要求管道预先在陆地厂房中进行焊接加工等预处理，然后螺旋缠绕到卷筒上进行储存，通过吊机吊装至铺管船上（部分铺管船直接在船上完成管道牵引和卷管作业），最后运送至指定作业区域开展铺管工作。

图1 管道螺旋缠绕于卷筒Fig.1 Pipe spiral winding on the reel

目前，国内外学者关于卷管式铺管安装研究主要集中在以下几个方面：1）管道椭圆度；2）管道局部缺陷；3）铺设过程中管道力学性能。卷管法铺管过程中管道会受到接触压力、弯曲和轴力等共同作用，可能会导致管道截面发生过度椭圆化进而引发失效破坏。Kyriakides等［3］发现管道椭圆化在一定程度上会削弱管道的抗弯刚度，甚至诱导海管发生结构失稳及局部屈曲。张九菊等［4］结合应变能法和Ritz 法推导基于深海卷管铺设管道椭圆度求解方法，探究影响海管椭圆度变化的主要参数及椭圆度变化规律。王立权等［5］指出管道在上卷至卷筒时最易发生失效，推导管道在各种失效形式下的管道极限承载公式。此外，张九菊等［6］建立考虑材料弹塑性的海管上卷加载、完全卸载、退卷加载及再次卸载等过程的曲率模型，阐明卷管铺设中海管的最优弯曲曲率及海管截面上的残余应力分布规律。Chatzopoulou 等［7］运用ABAQUS 有限元考虑材料包辛格效应及管道截面对称性建立二维管道半截面模型，研究卷管铺管过程产生的循环荷载对厚壁无缝钢管力学性能的影响，发现卷管循环荷载作用下钢管出现明显的截面椭圆化和材料各向异性现象。Ju 等［8］通过全尺寸卷管试验与有限元数值模拟相结合的方法，系统地研究管道径厚比、材料参数和轴向张力对卷管铺设过程中管道截面椭圆化和弯矩变化的影响规律。

在管道上卷过程中钢管焊缝缺陷和局部裂缝等因素会降低管道力学性能，甚至造成管道断裂和压溃等现象。Wästberg 等［9］研究卷管法铺管过程中局部焊缝缺陷对管道性能的影响。Yang 等［10］基于ABAQUS 有限元分别采用实体单元和刚体模拟钢悬链立管和卷筒，定义钢管母材和焊缝处的不同材料本构模型，研究未焊透和未融合两种焊缝缺陷对深海钢悬链立管卷管铺设过程中管道材料特性的影响。Jia等［11］在Budden和Ainsworth［12］、Nourpanah 和Taheri［13］的研究基础上，提出一种用于卷管法管道工程临界评价的改进参考应变法，研究管道几何形状、裂纹几何形状和材料性质对参考应变的影响。Lin等［14］研究循环拉压塑性变形对卷管铺设焊接管道的金属组织和力学性能的影响，分析变形错位与力学性能之间的内在联系。张九菊等［15］基于有限元软件ABAQUS 利用管道对称性建立含初始裂缝的三维实体局部模型模拟卷管铺设过程中受弯曲荷载作用下的变形过程，并拟合含裂缝管道的极限弯曲荷载表达式。李英和李婧一［16］指出相对于各向同性硬化材料模型，Ramberg-Osgood 材料模型能够更真实地模拟卷管法安装管道的力学响应，并研究焊接所致管道力学性能不均匀性的缺陷对卷管安装中管道性能的影响。刘书杰等［17］考虑不同层间黏结属性条件下夹层管卷筒式安装中缠绕和校直阶段力学行为，根据夹层管结构和载荷边界条件的对称性建立ABAQUS 1/4实体管道模型，研究海洋深水夹层管道残余应力和塑性应变的影响作用。

卷管式铺管法作业过程中管道会经历一系列的非线性弯曲和多次塑性变形，管道的力学性能会受到不同程度的影响。基于二维平面建模，胡显伟等［18］选择离散刚体单元构建校准器和卷筒，采用梁单元模拟立管，研究卷管法铺管上卷、退卷及校准3 个过程中管道应力—应变关系与累积塑性应变等响应特征，有效验证实际工程背景下卷管法铺管方案的可行性。白勇等［19］基于悬链线和小变形梁理论推导卷管法铺设柔性管的数值计算方法，运用理论方法和ABAQUS 数值模拟对柔性管的卷管铺设安装稳定性问题进行对比分析。Ashraf 等［20］采用壳单元建立不同直径、长度和增强层缠绕角度的ABAQUS 管段模型模拟卷管法铺管过程中RTP 管（增强热塑性塑料复合管）的力学性能和局部屈曲响应。廖洪千等［21］基于非线性环理论和虚功原理建立上卷过程管道截面应力和应变之间的平衡方程，通过ANSYS 数值模拟进行对比验证。Cho等［22］为论证双层管应用于卷管法铺管的可行性，基于有限元方法和滞回变形协调关系探究不同循环弯曲过程对双层管力学性能的影响。余杨等［23］推导管道退卷后残余轴向应力的解析解，并基于ABAQUS 有限元软件选择三维实体单元建立管道和卷筒，端部采用tie 约束并且考虑摩擦力作用，深入地研究卷管铺管法上卷过程张力和退卷过程后张力对管道椭圆度、截面轴向应力和剪切应力的影响。

综上所述，国内外学者主要以钢管为研究对象开展卷管铺管安装研究，少量文献涉及柔性管卷管铺设研究。而柔性管因其具有耐腐蚀性强、隔热性好、柔韧性好、质量轻、可回收利用、运输方便以及施工成本低等诸多优点广泛应用于深海油气田开发，由此可见对此类管道的研究重要性极高，且目前对柔性管的研究大多局限于采用梁单元模拟柔性管进行管道卷管过程力学响应。以直径为74 mm 的柔性管道为试验对象进行室内拉伸试验和弯曲试验，综合考虑柔性管的大轴向抗拉刚度和小抗弯刚度性能、几何非线性以及接触非线性等因素，根据试验数据建立两种柔性管上卷ABAQUS 有限元模型（梁—实体单元模型与壳和桁架—实体单元模型），基于数值模拟对比分析柔性管上卷过程中管道弯矩、弯曲曲率、管道轴力以及管道与卷筒接触压强等力学响应，为柔性管卷管铺设安装工程提供一定参考。

1 力学性能试验

1.1 尺寸参数

柔性管一般由多层结构组合而成，可以分为黏结柔性管（图2）和非黏结柔性管（图3）。黏结柔性管由织物、弹性纤维和钢材等各层结构通过压出、成型等物理方法挤压成一体，然后经硫化作用黏合在一起制造而成，一般适用于短节管，如跨接管等；非黏结柔性管由多层同轴的聚合物层和金属铠装层复合而成，主要包含骨架层、聚合物内护套、耐压铠装层、耐磨层、张力铠装层和聚合物外护套6个组成部分［24］。

图2 黏结柔性管横截面Fig.2 Cross section of bonded flexible pipe

图3 非黏结柔性管横截面Fig.3 Cross section of unbonded flexible pipe

非黏结柔性管的内部构成和层数并不固定，可根据项目的实际需求灵活调整。试验选取典型的非黏结柔性管（钢带缠绕增强复合管）进行柔性管卷管铺设研究，其管道结构主要由外层PE、中间钢带缠绕加强层以及内层 PE 组成（图4）。在柔性管铺管安装过程中，柔性管卷管变形属于非线性弹塑性大挠度变形。由于结构分层多样化和材料类型多元化导致柔性管力学性能存在显著的非线性特征，因此需要开展相应的力学试验获取柔性管力学性能属性及其破坏判断标准。试验样管的具体尺寸见表1。

表1 钢带缠绕复合柔性管试验样管参数Tab.1 Test sample pipe parameters of steel strip winding composite flexible pipe

图4 钢带缠绕复合管加工过程及其横截面Fig.4 Machining process and cross section of steel strip winding composite flexible pipe

1.2 拉伸试验

如图5 所示，采用3 000 kN 电磁控制万能试验机进行室内拉伸试验，需要注意以下几点：试件轴线与试验机夹具要对齐且保持均匀加载；试验测试需要确定温度和加载速度等条件；人工加载产生的误差需通过相同条件多组试验样管进行试验来控制。试验开始之前，首先需要检查试验样管，然后静置40 h 后开展拉伸试验，将试件端部通过法兰与试验机相连。根据ASTM D2105［25］标准规定，试件拉伸加载速度设置为0.1 mm/s；启动试验机，持续稳定加载直至试验样管拉断破坏（图6），通过动态信号测试系统同步实时记录试验过程中的荷载、位移以及时间等数据。

图5 拉伸试验Fig.5 Tensile test

图6 试验样管失效模式Fig.6 Failure mode of experimental sample pipes

拉伸试验采用指定恒定加载速度进行自动拉伸加载，开展两组钢带缠绕复合柔性管试验样管的拉伸试验，根据试验测得的拉力和位移数据处理获得的拉力—应变曲线，如图7所示。由于试验过程中存在不可避免的不可控因素，所得到的拉力—应变曲线表现出一定的波动性。但总体来说，两组拉力—应变曲线较为吻合，试验误差处于可控范围。采用DataFit数据拟合软件精确地拟合光滑拉力—应变曲线，根据ISO 527—2010 标准［26］定义，柔性管的拉伸模量取为应变分别为0.05%和0.25%处的割线模量，即Et=（σ1−σ2）/（ε1−ε2）。其中，σ1为应变0.05%（ε1）处的截面应力，σ2为应变0.25%（ε2）处的截面应力。根据拉伸试验结果，该钢带缠绕复合柔性管的拉伸模量为1 554.3 MPa。

图7 拉伸试验曲线Fig.7 Tensile test curve

1.3 弯曲试验

国内外学者普遍采用三点弯曲或者四点弯曲开展管道弯曲试验研究其弯曲性能。三点弯曲试验加载方式简单，但由于加载方式集中，弯曲分布不均匀，中间施加力部分可能会出现应力集中，达不到效果。而四点弯曲试验弯矩均匀分布，试验结果较为准确，但压夹结构复杂，工业生产中较少采用。弯曲试验采用四点弯曲加载方法以保证纯弯段的存在，同时为消除重力因素对结果的影响，试验在水平面内进行。如图8所示，弯曲试验设备主要包含千斤顶、力传感器、位移计、加载梁和滚轮支座等。通过力传感器和位移计及试验器材的尺寸推导出弯矩和曲率。试验选取两组试件在相同条件下进行以克服人工加载方式产生的误差，试件中截面保证对中（图9），注意加载速度匀速平缓，当管道出现局部屈曲立即中止加载（图10）。

图8 弯曲试验设备Fig.8 Bending test equipment

图9 弯曲前的柔性管试件Fig.9 Flexible pipe specimen before bending

图10 弯曲后的柔性管试件Fig.10 Flexible pipe specimen after bending

四点弯曲试验采用单调分级加载机制，其中预加载所用荷载是分级荷载前 2 级，正式加载的加载速度设置为1.66 mm/s。试验开始前测量试件尺寸和各试验参数，并检查试件是否有可见缺陷、划痕和瑕疵。一切准备就绪后，通过千斤顶施加荷载作用于加载梁上，使其按照设置加载速度稳步加载，直至荷载出现下降后停止加载。同步实时记录试验过程中的荷载、位移以及时间等数据，基于几何关系和测量的荷载—位移参数，计算得到柔性管弯曲—曲率曲线（图11）。将图11中两组数据拟合后，得到一条较为光滑稳定的曲线，由于模型模拟的卷筒半径为3 m，故选取曲率在0.33 m-1处切线模量作为柔性管等效弹性模量E1=ΔM/（Δκ·I）=491.96 MPa，其中，ΔM为弯矩变化量，Δκ为曲率变化量，I为截面惯性矩。

图11 弯曲试验曲线Fig.11 Bending test curve

2 卷管铺设上卷有限元建模

以“海洋石油286”铺管船为原型［27］（图12），建立卷管铺设有限元模型，“海洋石油286”铺管船内置转盘参数如表2 所示［28］。卷管铺设有限元模型可以简化为两个主要部件，即卷筒与管道。卷筒直径大小与管道上卷过程中受到的曲率和弯矩等荷载息息相关，为了验证管道在上卷作业极限状态下的力学性能是否处于安全性能范围内，卷筒模型直径选取最小值，即6 m。

表2 内置转盘参数（海洋石油 286）Tab.2 Built⁃in turntable parameters（HYSY 286）

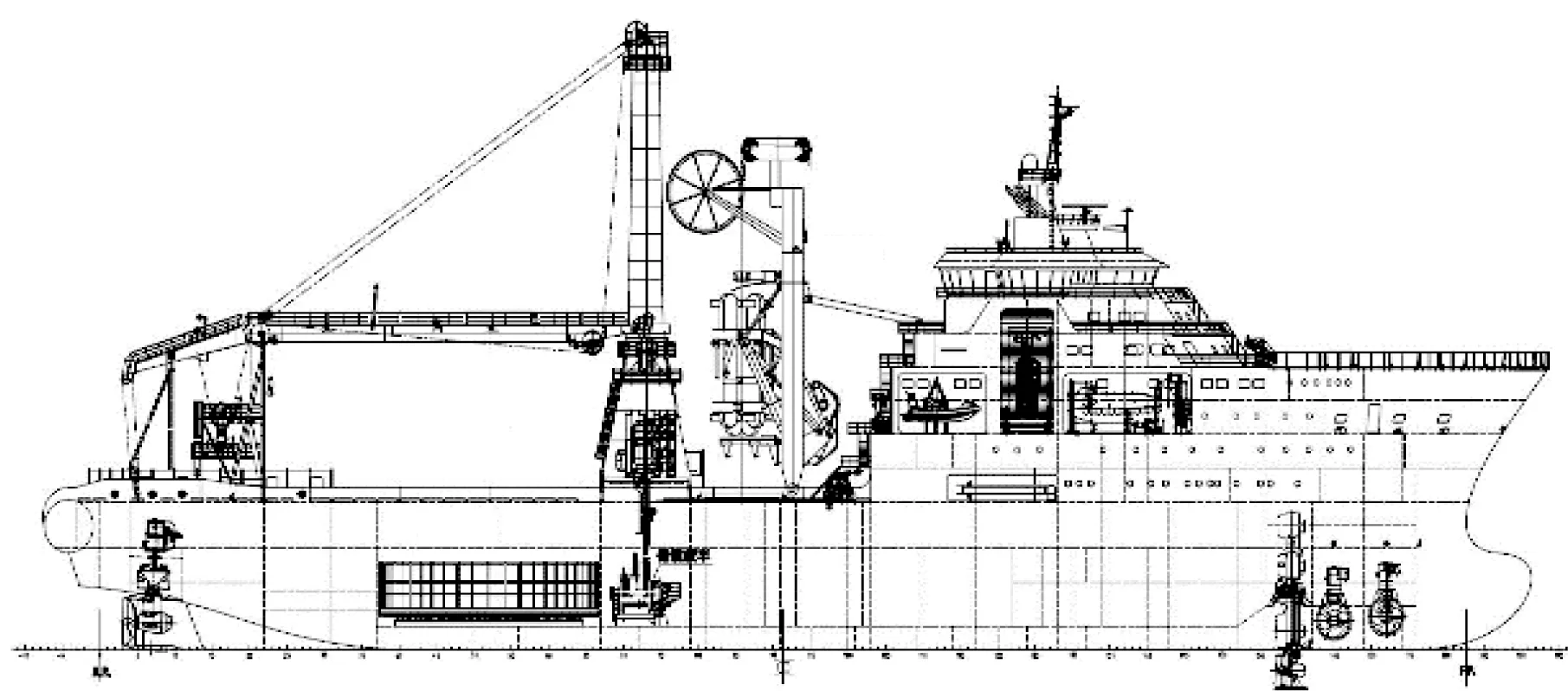
图12 “海洋石油 286”布置示意Fig.12 Layout plan of “HYSY 286”

鉴于柔性管是由螺旋加强层和聚合物密封层组合而成的多层复合结构，其力学特征表现为较大的轴向抗拉刚度和较小的抗弯刚度。而国内外很多学者研究长度较大的柔性管受力性能时，普遍将柔性管多层结构等效为单层均质结构（实体或壳单元），基于抗弯刚度等效原则推导单层均质结构的等效弹性模量，这样可以大大地降低模型的建模难度并且有效地提高模型的计算效率及其收敛性。但是，这种简化处理将会导致该等效单层均质结构的抗拉刚度严重偏低，进而影响有限元模型数值模拟的精确性和有效性。因此，文中提出两种卷管铺设有限元模型（梁—实体有限元模型和壳&桁架—实体单元模型），充分考虑柔性管大拉伸刚度和小弯曲刚度并存的特性，深入地研究柔性管在卷管铺设上卷过程中的力学性能和变形特征。

2.1 梁—实体有限元模型

2.1.1 建模

如图13所示，卷管铺设有限元模型包含卷筒和柔性管两大部件。柔性管的力学性能通过室内拉伸试验和弯曲试验获得，试验得到的非线性拉力—应变与弯矩—曲率关系作为柔性管部件的关键建模参数。卷管铺设上卷过程缠绕的管道质量可达数千吨［29］，为了减少有限元数值模拟计算量和存储量，这里截取80 m 长度建立柔性管B31梁单元模型，该单元为Timoshenko梁单元，与Euler-Bernoulli梁单元相比，该单元既能够考虑轴向变形、弯曲变形和扭转变形，还可以考虑一阶剪切变形。梁单元采用广义截面，通过在Keywords Editor 模块中编辑inp 文件分别定义柔性管非线性抗弯刚度和抗拉刚度。这样可以在保证模型在考虑到柔性管非线性力学特性的前提下以较低的计算代价输出轴力、弯矩和曲率等主要力学性能指标，同时提高模型的收敛性。卷筒采用C3D8R单元建模并进行网格划分（图14），对柔性管与卷筒的接触区域采取网格细化处理，确保柔性管与卷筒非线性接触精确模拟的同时，尽可能降低数值模拟的计算量。

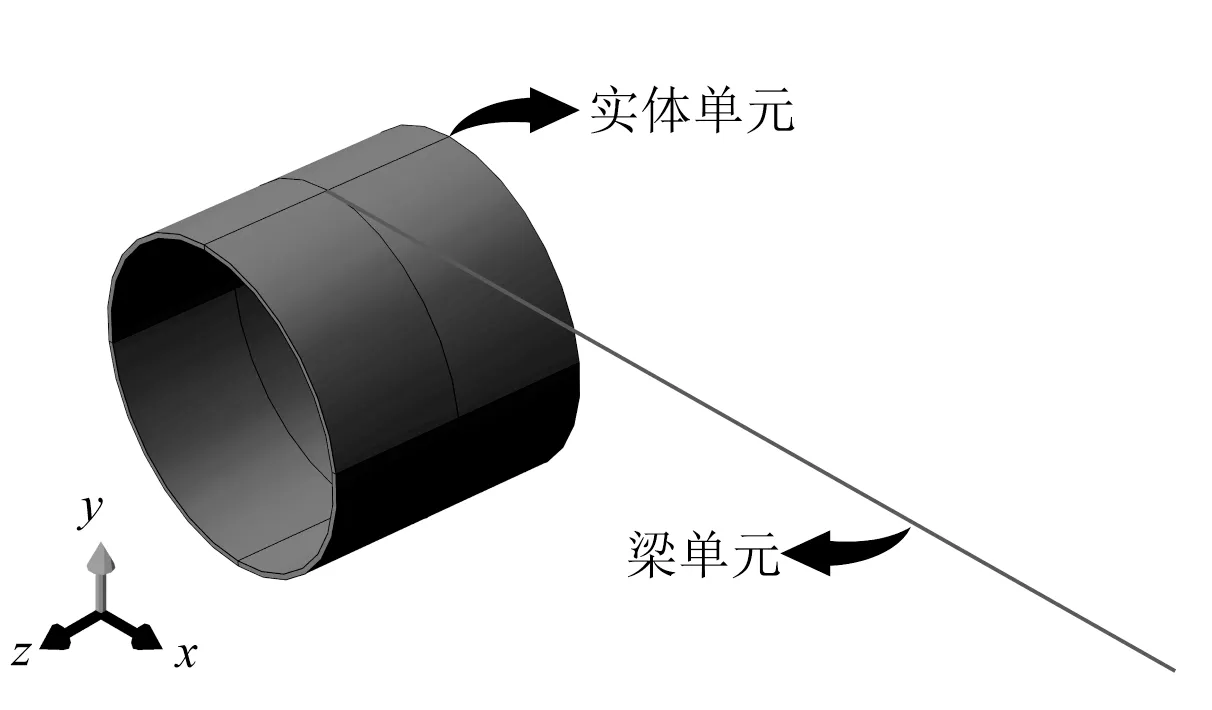
图13 梁—实体有限元模型Fig.13 Beam-solid finite element model

图14 梁—实体有限元模型网格划分Fig.14 Beam-solid finite element model meshing

2.1.2 相互作用及载荷设定

相互作用设定是有限元模型不同部件之间的纽带，柔性管和卷筒两个部件通过定义接触和约束条件实现不同部件之间的非线性接触和边界约束条件。柔性管与卷筒接触的法向行为和切向行为分别采用“硬接触”和“罚函数”进行定义，其中“罚函数”模块中摩擦系数设置为0.2［30］。柔性管与卷筒之间的相互作用类型选择“面面接触”，鉴于卷筒刚度远大于柔性管，因此将卷筒外表面设置为主表面，柔性管设置为从表面。

如图15 所示，卷筒中心处设置一参考点RP，将整个卷筒耦合到参考点RP，通过定义参考点RP 的边界条件（只保留RP 绕Z轴的转动自由度，锁止其他自由度）实现卷筒上卷作业。根据“海洋石油286”铺管船内置转盘最大转速为0.094 rad/s，取70%最大转速为卷筒模型转速，即参考点RP 在Z轴正方向的转动速度设置为0.065 8 rad/s。将柔性管靠近卷筒一侧的端点耦合于参考点RP，保证柔性管在卷筒转动过程中顺利上卷；在柔性管自由端施加一15 kN 的集中荷载（牵引力），保证柔性管在上卷过程中始终保持张紧状态，并在平行于Z轴正方向上施加位移约束条件以保证柔性管在上卷过程中螺旋缠绕于卷筒。

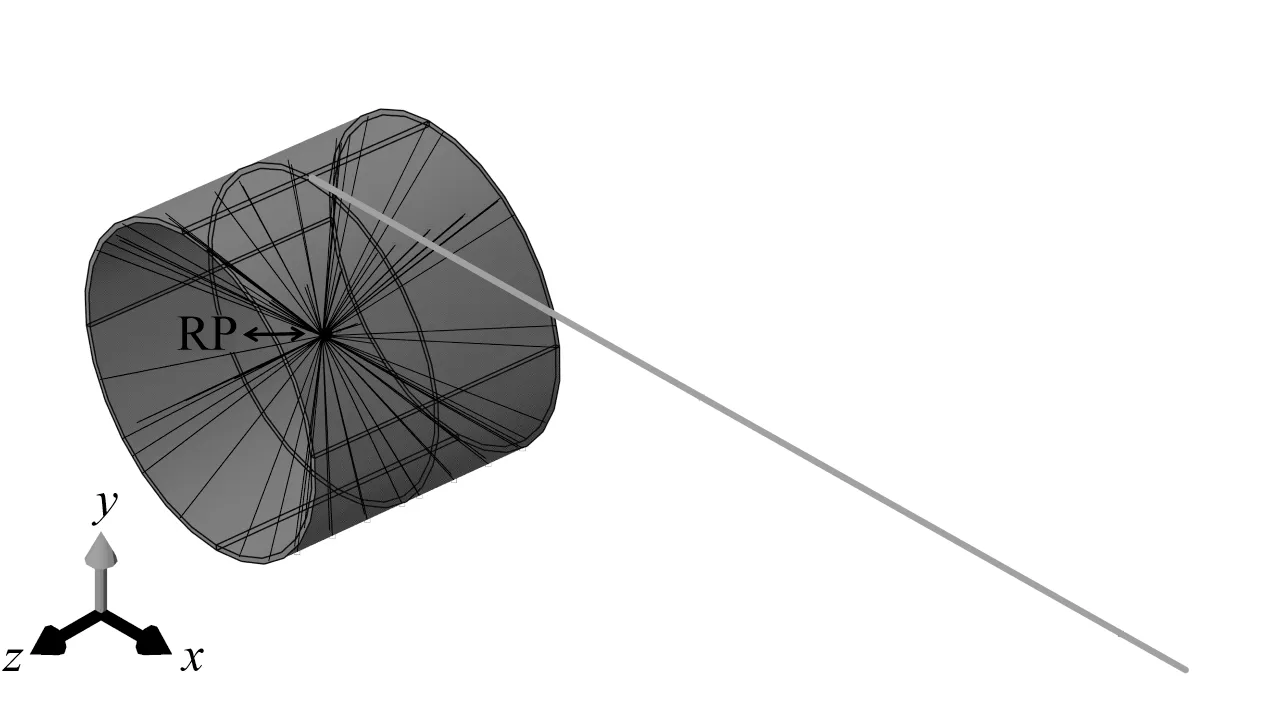
图15 梁—实体有限元模型载荷条件Fig.15 Beam-solid finite element model load conditions

2.2 壳和桁架—实体单元模型

2.2.1 建模

国内外学者普遍采用实体或壳单元模拟钢管缠绕于卷筒的力学特征，基于恒定弹性模量表征钢管的抗拉刚度和抗弯刚度两个维度。针对柔性管卷管铺设，鉴于柔性管较小抗弯刚度和较大抗拉刚度并存等力学性能，无法基于恒定弹性模量表征其抗拉刚度和抗弯刚度两个维度。因此，构建壳和桁架—实体单元模型（图16），通过引入抗弯刚度为0的桁架单元弥补实体或壳单元在保证柔性管较小抗弯刚度前提下抗拉刚度不足的缺陷。桁架单元的特点是只能承受拉、压轴向荷载，不能承受弯矩，该特性可以在补足轴向抗拉刚度的同时，确保柔性管的抗弯性能。壳和桁架—实体单元模型包含壳单元、桁架单元以及实体单元3 个部件。其中，壳单元（S4R）与桁架单元（T3D2）组合结构模拟柔性管，较梁—实体有限元模型更为复杂，可以有效地模拟柔性管和卷筒之间的相互作用和接触压力。如图17 所示，建立壳单元的局部模型，便于数值模拟结果的管道力学数据提取。其中，局部坐标中1、2和3方向分别代表管道切线、主法线及副法线方向。

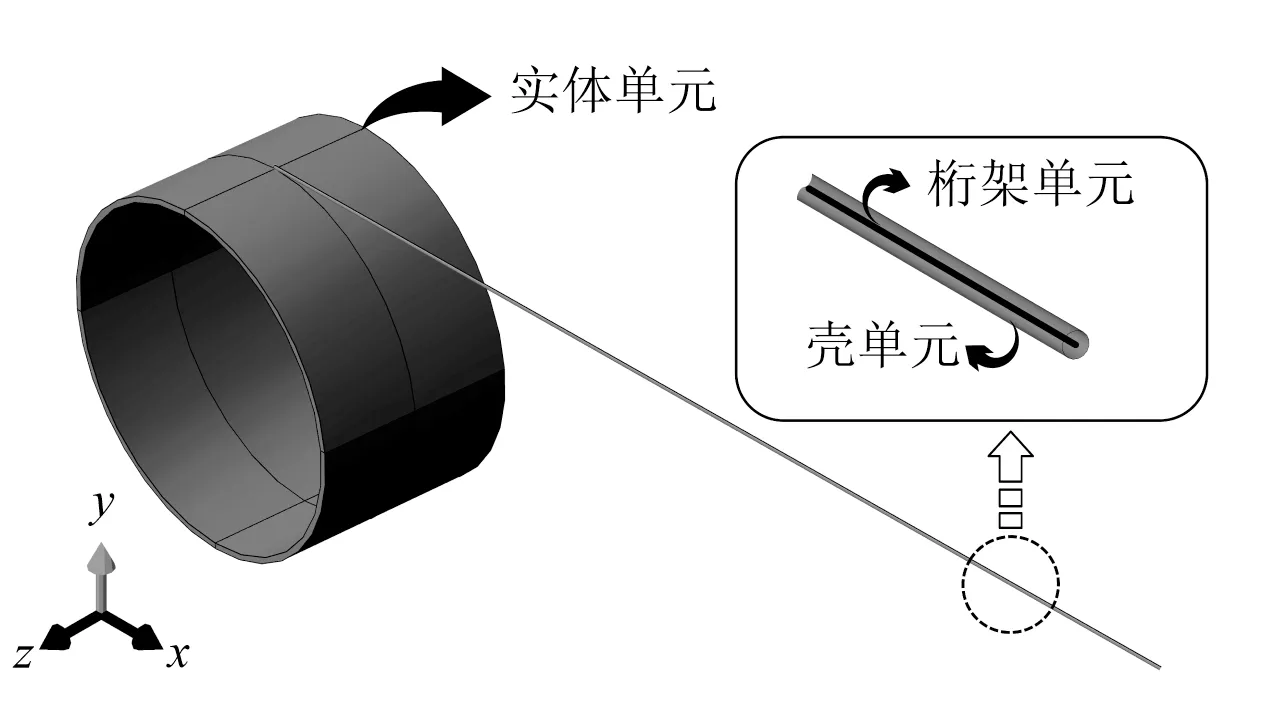
图16 壳和桁架—实体有限元模型Fig.16 Shell & truss-solid finite element model

图17 管道弯矩方向示意Fig.17 Diagram of pipe bending moment direction

通过室内样管拉伸试验得到真实的柔性管拉力—应变曲线（图7），依据ISO 527—2019［26］推算柔性管轴向抗拉刚度EA=3 632.51 kN。通过室内样管弯曲试验得到弯矩—曲率曲线（图11），推算柔性管等效弯曲弹性模量E1=491.96 MPa。基于等效弯曲弹性模量可以计算得到壳单元模型轴向抗拉刚度为1 149.71 kN，远远小于该柔性管真实的轴向抗拉刚度（EA=3 632.51 kN）。由此可见，采用桁架单元弥补壳单元拉伸刚度不足是非常必要的。为了精确模拟卷筒与柔性管非线性接触响应，同样对柔性管与卷筒的接触区域进行网格细化处理，壳单元部件横截面圆周方向划分16个单元，壳单元和桁架单元的轴向单元长度选取为100 mm进行网格划分。

2.2.2 相互作用及载荷设定

壳和桁架—实体单元模型相互作用设定与梁—实体有限元模型基本一致，但是由于壳和桁架—实体单元模型的部件数量（3个）多于梁—实体有限元模型（2个），因此壳和桁架—实体单元模型的边界条件较梁—实体有限元模型更为复杂，主要表现为不同部件之间多个自由度的耦合。如图18所示，卷筒的边界条件、柔性管和卷筒之间的耦合边界以及荷载施加设定与梁—实体有限元模型相同，主要区别在于柔性管部件，将柔性管壳单元首尾两端截面和桁架单元两端耦合到截面中心点（RP1 和RP2），有效地保证了柔性管壳单元与桁架单元组合结构在上卷过程中保持协同。

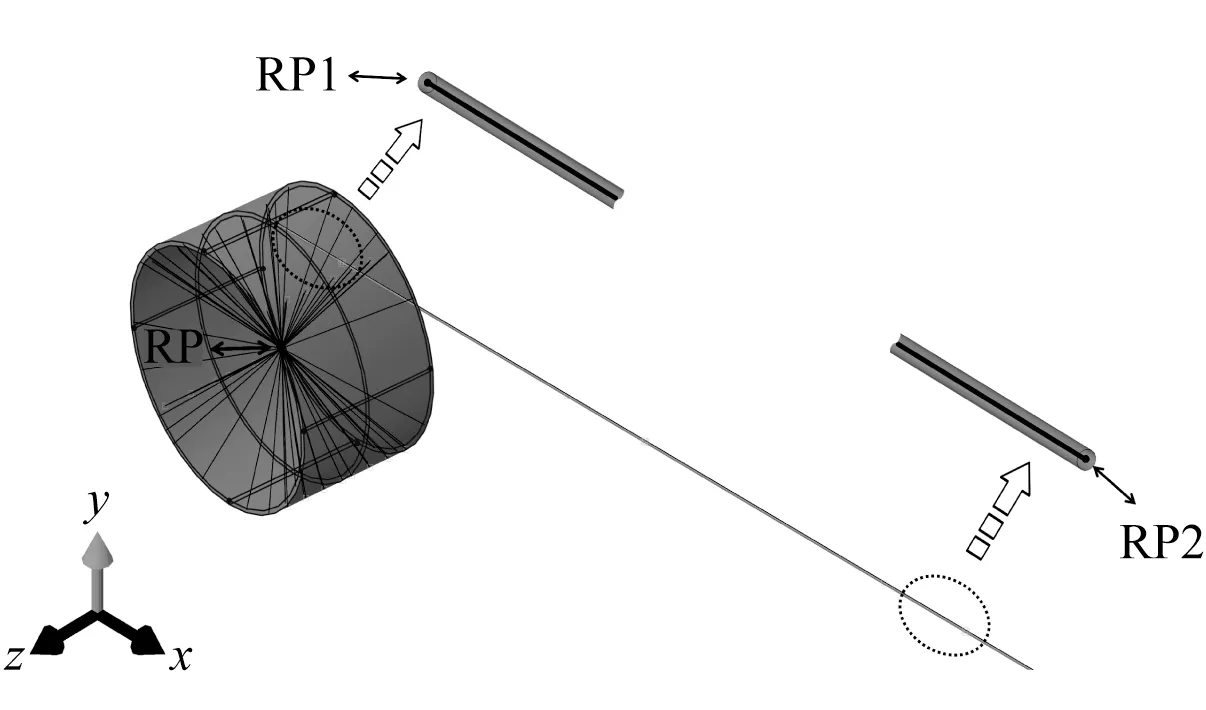
图18 壳和桁架—实体有限元模型载荷条件Fig.18 Shell & truss-solid finite element model load conditions

3 结果与讨论

根据卷管位置和管道受力特征，将柔性管分为以下4个部分（如图19所示）进行讨论分析：1）起始段，即管道起点附近的管段，这一段管道由于端部效应和约束条件等因素的影响，数值波动较大，可能与实际情况存在一定偏差；2）弯曲段，管道上卷至卷筒并与卷筒贴合的完全弯曲部分；3）过渡段，管道与卷筒的临界接触区域，该区域伴随着弯矩以及轴力的突变；4）直线段，管道未上卷于卷筒的直线部分，该段管道未发生弯曲，所受弯矩荷载较小且受力较为单一。

图19 卷管有限元模型分段说明Fig.19 Section description of pipe finite element model

3.1 弯曲曲率分析

卷管铺设过程中管道的弯曲和曲率是非常重要的力学响应，也是国内外研究的重点，同时是制约卷筒直径的控制因素。如图20所示，两种卷管铺设有限元模型中管道沿着其副法线的弯矩（SM3）从起始段延伸到弯曲段区域基本保持水平直线，进入过渡段区域时管道SM3弯矩急剧下降至0，最后在直线段区域基本保持在0 上下波动。起始段延伸到弯曲段区域的管道SM3 弯矩基本保持常数，这是由恒定直径的卷筒约束作用所导致的。

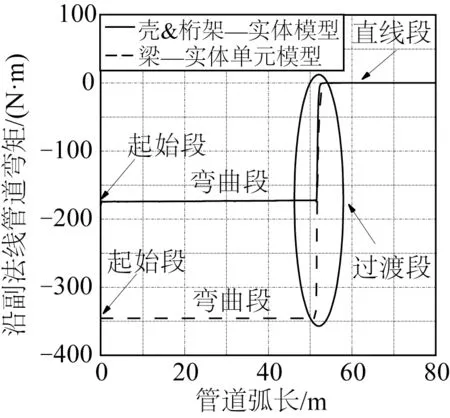
图20 沿管道弧长分布的副法线方向管道弯矩Fig.20 Pipe bending moment in the secondary normal direction distributed along the arc length of the pipe

通过对比发现，梁—实体有限元模型起点段和弯曲段SM3弯矩数值约为壳和桁架—实体有限元模型的两倍左右。这是由于梁—实体有限元模型通过在Keywords Editor 模块中编辑inp 文件定义柔性管非线性抗弯刚度，其弯矩—曲率的力学性能与试验得到的非线性曲线保持一致；而壳和桁架—实体有限元模型采用等效均质壳单元模拟柔性管，其弹性模量为恒值（即抗弯刚度为恒值），文中选取弯矩—曲率曲线在0.33 m-1处的切线模量作为柔性管的等效弹性模量。经计算，梁—实体单元有限元模型中管道在0.33 m-1曲率处的抗弯刚度为1 037 N∙m2，而壳和桁架—实体单元有限元模型中管道的抗弯刚度为573 N∙m2。故在相同的卷筒直径（弯曲半径）工况下，梁—实体单元有限元模型管道抗弯刚度约为壳和桁架—实体单元有限元模型管道抗弯刚度的两倍，最终导致梁—实体有限元模型起点段和弯曲段SM3弯矩数值约为壳和桁架—实体有限元模型的两倍左右。

但是，在相同的卷筒直径（6 m）工况下，两种有限元模型管道弯曲段的曲率非常接近（图21），有力地验证两种有限元模型的有效性和准确性。从图21可以看出，梁—实体有限元模型管道弯曲段曲率大约保持在0.333 m-1左右，而壳和桁架—实体有限元模型管道弯曲段内外侧曲率则分别为0.332 m-1和0.328 m-1。由于柔性管沿着卷筒螺旋缠绕储存运输，所以管道弯曲段曲率要略小于卷筒的曲率0.333 m-1。此外，柔性管螺旋缠绕导致产生沿着其切线和主法线的SM1和SM2弯矩，但其值远小于沿着副法线的SM3弯矩。

图21 沿管道弧长分布的管道曲率Fig.21 Pipe curvature distributed along the arc length of the pipe

综上所述，两种模型在分析弯曲曲率方面互有优劣，其中梁—实体有限元模型可以直接、准确地输出管道曲率，但是无法模拟管道空间结构致使管道截面曲率为恒值；而壳和桁架—实体有限元模型能够较为真实地模拟管道弯曲后其横截面的曲率分布，但是需要设置路径才能提取曲率，操作较为复杂。

3.2 管道轴力分析

实际工程一般在岸边船坞完成管道卷管铺设的上卷作业，通过选取合适的牵引力实现管道顺利螺旋上卷。而管道上卷的牵引力与管道轴力息息相关，过大的牵引力可能会导致管道轴力过大，进而导致上卷管道发生拉伸破坏和椭圆化屈曲。如图22 所示，梁—实体有限元模型中柔性管轴力基本维持在15 kN 左右，这与柔性管自由端施加的15 kN牵引力比较吻合。而壳和桁架—实体有限元模型中柔性管轴力从起始段到弯曲段逐渐增大，在过渡段区域出现突变峰值，最后迅速下降到直线段15 kN。两种有限元模型的柔性管直线段轴力基本控制在15 kN 左右，符合预期结果，但壳和桁架—实体有限元模型中柔性管起始段、弯曲段和过渡段轴力与预期的15 kN存在较大的偏差。该壳和桁架—实体有限元模型综合考虑了管道与卷筒之间的摩擦效应、桁架单元纯拉伸作用以及管道螺旋缠绕产生的侧向位移等因素，研究发现管道与卷筒之间的摩擦效应是导致壳和桁架—实体有限元模型中柔性管起始段、弯曲段和过渡段轴力数值偏小的主要原因（图22）。

图22 沿管道弧长分布的管道轴力Fig.22 Pipe axial force distributed along the arc length of the pipe

此外，壳和桁架—实体有限元模型中柔性管受到的轴力主要包含两部分：壳单元轴力以及桁架单元轴力。通过提取壳和桁架—实体有限元模型中壳单元和桁架单元的轴力，发现桁架单元沿着管道弧长也基本保持不变，其数值在4 kN左右波动；而壳单元由于受到轴力和弯矩的共同作用，其横截面上各壳单元的单位厚度节点轴力变化较大。图23为两种工况（考虑摩擦和不考虑摩擦）壳和桁架—实体有限元模型的弯曲段、过渡段和直线段3 个横截面沿着圆周方向的壳单元单位厚度节点轴力分布，该分布曲线呈现对称性（沿202.5°对称分布）。从图23 中可以看出，考虑摩擦的壳和桁架—实体有限元模型的弯曲段区域横截面的单位厚度节点轴力小于无摩擦力模型，因此考虑摩擦的壳和桁架—实体有限元模型弯曲段轴力要小于无摩擦力模型；而考虑摩擦的壳&桁架—实体有限元模型的过渡段区域横截面的单位厚度节点轴力略大于无摩擦力模型，与过渡段区域出现突变峰值现象吻合。

图23 沿管道横截面分布的单位厚度节点轴力Fig.23 Nodal axial force per unit thickness distributed along the cross section of the pipe

由于壳单元的横截面沿着圆周方向均匀划分16个网格单元，故横截面网格单元划分关于XY平面对称。但是，由于管道螺旋缠绕于卷筒上，管道不仅承受沿着副法线的弯矩（SM3），而且还承受沿着主法线的弯矩（SM2），因此壳单元横截面上单位厚度节点轴力虽然也是对称分布，但并非是关于XY平面对称，而是发生一定转动（图23）。通过对管道横截面上各节点单位厚度轴力对比分析，可以发现壳单元弯曲段表现为一侧受压、一侧受拉，管道横截面圆周角在112.5°～292.5°附近区域，管道横截面上各节点单位厚度轴力表现为轴向受压，且该区域对称位置（202.5°）处的管道横截面上节点单位厚度轴向压力达到最大值；横截面圆周角在292.5°～112.5°附近区域，管道横截面上各节点单位厚度轴力表现为轴向受拉，且该区域对称位置（22.5°）处的管道横截面上节点单位厚度轴向拉应力达到最大值。如图24所示，提取壳和桁架—实体有限元模型中壳单元横截面22.5°～202.5°共9 个节点沿着管道弧长的单位厚度节点轴力分布参数进行研究分析。通过对管道横截面上各节点单位厚度轴力对比分析，可以发现壳单元弯曲段横截面圆周角202.5°处的单位厚度节点轴力最小（受SM2和SM3弯矩影响），从侧面验证管道轴力分布规律的正确性。

通过对比可以发现，梁—实体有限元模型可以直接输出管道轴力，操作简便，但是该模型无法有效地考虑摩擦力的影响作用；壳和桁架—实体有限元模型可以模拟管道横截面不同位置的轴力分布情况特征，但是其横截面轴力包含桁架单元和壳单元受到的轴力两个部分，需要对数据进行处理，操作较为复杂。

3.3 接触压强分析

管道螺旋上卷于卷筒过程中，管道与卷筒之间为刚性接触，当其接触压强过大时，可能导致管道发生屈曲失稳。图25和图26分别为梁—实体有限元模型和壳和桁架—实体有限元模型管道上卷过程中卷筒最大接触压强应力CPRESS 云图。通过ABAQUS 有限元数值模拟，发现管道与卷筒的最大接触压强主要发生在过渡段区域。其中梁—实体有限元模型的最大接触压强发生在卷筒壳单元843#节点处，最大值区域为圆点状，其值为1.89 MPa；而壳和桁架—实体有限元模型的最大接触压强发生在卷筒壳单元596#节点处，最大值区域为条带状，其值为0.65 MPa。通过对比发现，壳和桁架—实体有限元模型数值模拟得到的最大接触压强远小于梁—实体有限元模型，可能是因为壳和桁架—实体有限元模型采用壳单元和桁架单元模拟柔性管，可以比较真实地模拟柔性管与卷筒之间的非线性接触；而梁—实体有限元模型将柔性管简化成一条线（梁单元），无法有效地模拟管道与卷筒之间的接触面积变化，因此数值模拟得到的接触压强偏大。

图25 卷筒接触压强云图（梁—实体有限元模型）Fig.25 Reel CPRESS cloud diagram (Beam-solid FEM)

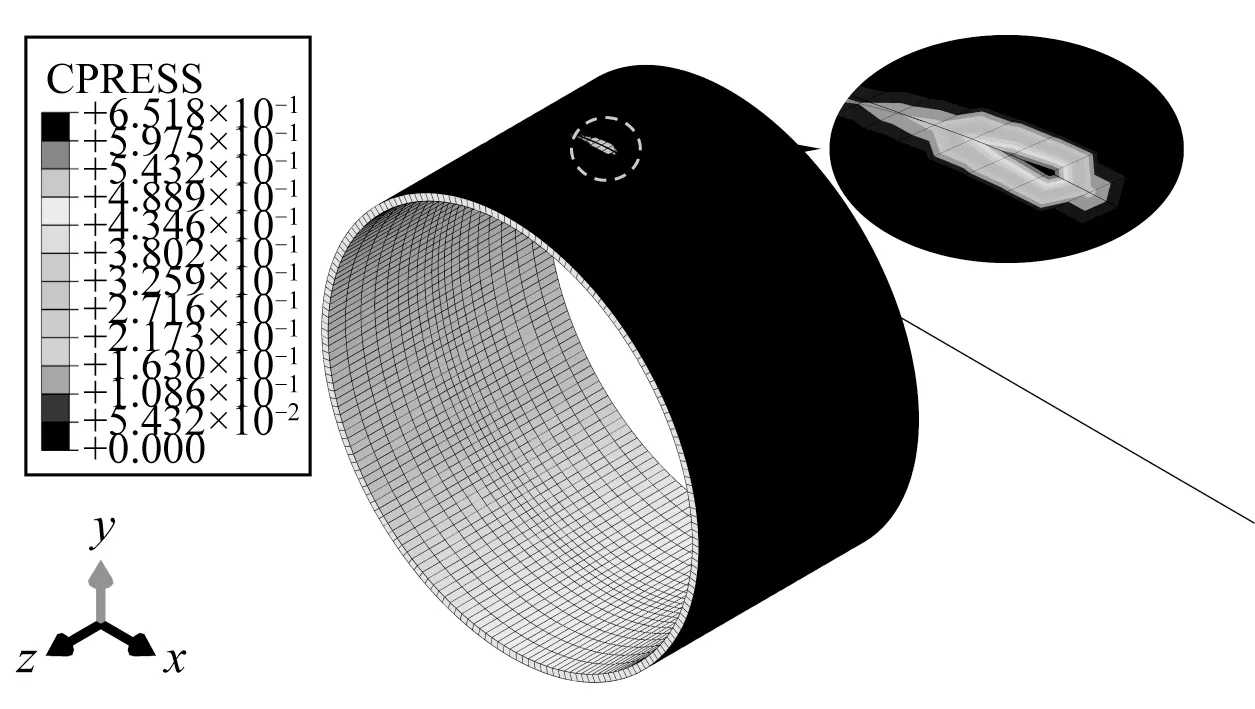
图26 卷筒接触压强云图（壳和桁架—实体模型）Fig.26 Reel CPRESS cloud diagram (Shell & truss-solid FEM)

图27为梁—实体有限元模型最大接触压强843#节点和壳和桁架—实体有限元模型最大接触压强596#节点的时间历程响应。从图27 中可以看出，模型卷筒最大接触压强发生在管道过渡段上卷于卷筒时刻，当管道继续上卷时，该管道与卷筒接触区域的接触压强会急剧下降，然后趋于平缓。此外，壳和桁架—实体有限元模型壳单元596#节点的接触压强由于摩擦力的影响也不断下降。图28 和图29 分别为梁—实体有限元模型和壳和桁架—实体有限元模型管道上卷过程中卷筒最大接触剪切应力CSHEAR1云图，分别为0.014 MPa 和0.13 MPa。综上所述，针对管道与卷筒接触压强模拟，壳和桁架—实体有限元模型数值比梁—实体有限元模型更有优势，可以较为准确地模拟管道与卷筒之间的接触压强。

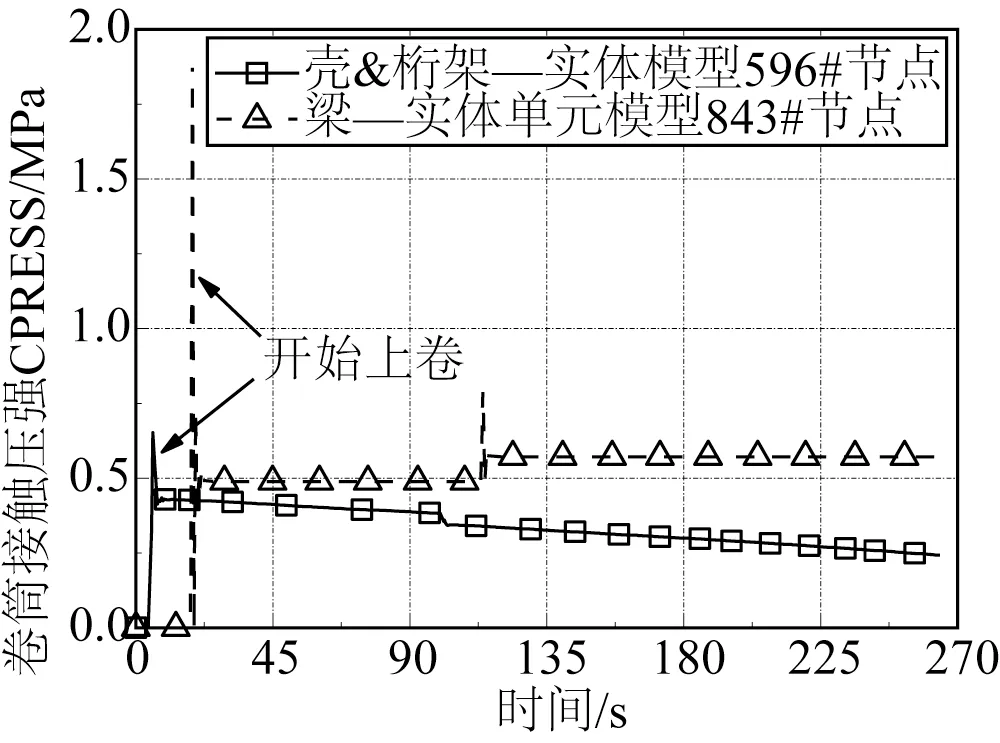
图27 节点最大接触压强时间历程响应Fig.27 Time history response of maximum nodal CPRESS

图28 卷筒接触剪应力云图（梁—实体模型）Fig.28 Reel CSHEAR1 cloud diagram (Beam-solid FEM)

图29 卷筒接触剪应力云图（壳和桁架—实体模型）Fig.29 Reel CSHEAR1 cloud diagram (Shell & truss-solid FEM)

4 结 语

为准确模拟卷管铺管法柔性管上卷过程，通过全尺寸柔性管力学性能试验获得柔性管轴力—应变以及弯曲—曲率等非线性力学性能关系，基于ABAQUS 商用有限元软件建立两种柔性管上卷有限元模型（梁—实体单元模型与壳和桁架—实体单元模型），实现柔性管较大轴向抗拉刚度和较小抗弯刚度的同步模拟。通过对比分析两种有限元模型数值模拟得到的管道弯矩、弯曲曲率、管道轴力、管道与卷筒接触压强等关键数据，得出以下结论：

1）在卷管铺管法管道上卷过程中，管道沿副法线方向的SM3 弯矩占据管道弯曲变形主导地位，柔性管螺旋缠绕导致产生沿切线和主法线方向的SM1和SM2弯矩，但其值远小于沿着副法线的SM3弯矩。

2）通过分析管道轴力沿管道弧长的分布，发现管道与卷筒之间的摩擦效应对于管道轴力的影响较为显著，在实际工程中需要考虑摩擦力对管道轴力和轴向变形的影响作用。

3）管道与卷筒的最大接触压强主要发生在卷管过渡段区域。相对比于梁—实体单元模型，壳和桁架—实体有限元模型采用壳单元和桁架单元模拟柔性管，可以比较真实地模拟柔性管与卷筒之间的非线性接触。

4）对比两种有限元模型可以发现，壳和桁架—实体单元模型能够更为真实地模拟管道的力学响应（管道弯曲曲率、截面应力及应变、管道与卷筒接触压强等），但是计算工作量比梁—实体有限元模型大。