锚链和锚链轮刚柔耦合动力学建模及啮合过程力学分析

李文华，刘雄雁，林珊颖，周性坤，韩凤翚，潘瑞祥

(1.大连海事大学 轮机工程学院，海底工程技术与装备国际联合研究中心,辽宁 大连 116026；2.南通力威机械有限公司,江苏 如皋 226500)

深水定位时，锚泊定位系统工作负载大，锚链和锚链轮啮合故障时有发生。

关于锚链和锚链轮的研究，没有将锚链和锚链轮配合为整体进行分析，只单独对锚链轮进行理论分析，与实际情况存在一定的差别[1-4]。要么侧重于机架和整体的研究，并且只进行了静态的仿真分析，并没有考虑锚链-锚链轮啮合全时动态受力情况[5-6]。为此，针对海上作业抛锚过程中锚链和锚链轮的运动状况，对半潜式“勘探三号”钻井平台锚泊定位系统中的锚链轮，采用ANSYS软件建立锚链和锚链轮的刚柔耦合模型，同时对抛锚时锚链和锚链轮啮合过程理想状态下，锚链环和锚链轮的接触点进行受力分析，分别对锚链环“进入-啮合-离开”锚链轮三种状态进行受力分析，得到锚链环和锚链轮接触点压力和时间的函数关系，并通过所建立的刚柔耦合模型进行仿真验证，为锚泊定位系统锚链轮与锚链的结构设计与优化提供参考。

1 锚链与锚链轮刚柔耦合模型

1.1 锚链轮建模

半潜式“勘探三号”钻井平台锚泊定位系统锚链轮实物图与通过SolidWorks等比例建立的模型见图1。

图1 锚链轮实物及模型

选取A型5齿锚链轮，见图2，以2个剖面表示5齿锚链轮的主要轮廓，图2中，承窝底面和轮齿所包括的部分为连环承窝，这也是锚链和锚链轮啮合过程中主要的受力区域，在链环承窝要承受来自各个方向的扭矩、牵引和冲击。

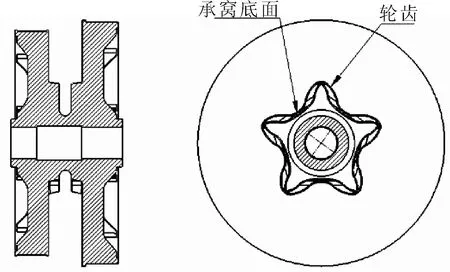
图2 锚链轮结构示意

1.2 锚链建模

选取无档电焊锚链，根据所建立的锚链轮模型，按照国际标准ISO21711通过SolidWorks设计锚链环模型，并装配成锚链模型。见图3，包括正视图和剖视图，公称直径D=76 mm，锚链环的链接方式见图4。为了方便研究，选择中间链节链接的锚链环连接形式。链接卸扣是用于链节和链节之间的链节，因此主要分析1节锚链和锚链轮的啮合情况，考虑锚链卸扣。

图3 锚链环结构示意

图4 锚链3D模型

1.3 锚链和锚链轮刚柔耦合模型建模

锚链和锚链轮的啮合过程属于典型的环型链啮合传动，具有链传动的基本特点即传递功率大、传递效率高、过载能力强和对环境要求低等优点，与其他链传动的链轮形式不同之处在于外出包角和轮齿的形式。普通的链传动的链轮外出包角为180°，并且1个轮齿中间没有间隙；锚链轮的外出包角一般在120°左右，1个轮齿中间存在间隙。因此锚链和锚链轮之间的啮合配合和其他链传动之间的配合存在差别。

根据半潜式“勘探三号”钻井平台锚泊定位系统锚链轮在试验中的啮合情况进行建模，去除轴承等非必要约束元件，并且设计简易支架，通过ANSYS的transient structual模块，定义锚链、锚链轮和轴的刚度特性为Flexible，机架刚度特性为为Rigid。轴和锚链轮之间为Fixed连接，轴和机架之间为Revolute连接。锚链轮和各个锚链环之间接触设定为Frictional，各个锚链环之间接触为Bonded。锚链的运动副设定有Revolute和Translational 2种。同时在锚链首端锚链环增加拉力，建立锚链和锚链轮刚柔耦合模型见图5。

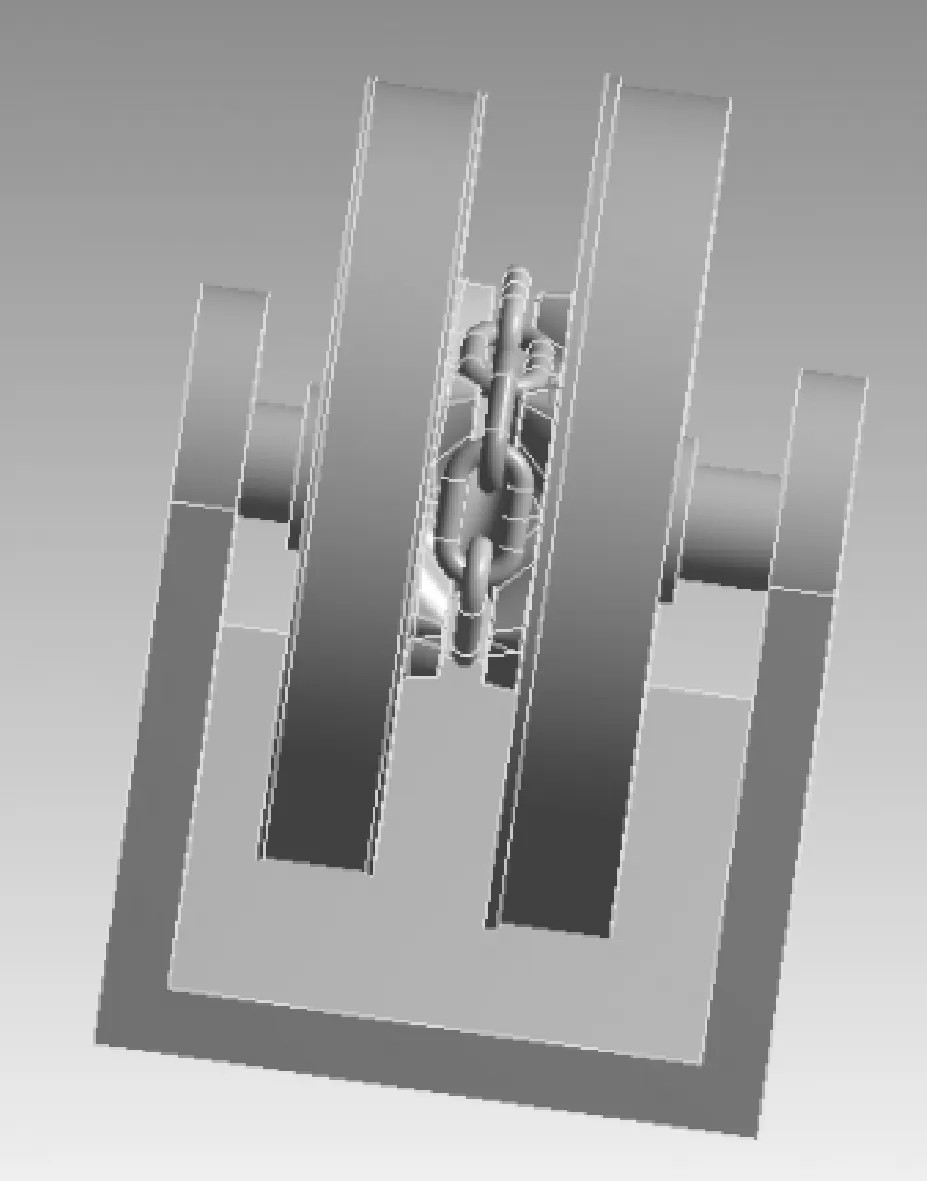
图5 锚链和锚链轮刚柔耦合模型

锚链和锚链轮啮合过程示意于图6。通过图6可知，锚链和锚链的理想啮合状态是链窝和链齿部分各有一个锚链环，在链窝里的锚链环水平放置在链窝中；在链齿部分的锚链环竖直放置在轮齿间。当普通锚链环处于链环承窝中间时，普通链环处于链窝位置时, 其前后端的链径中心的轨迹圆，称为基圆。

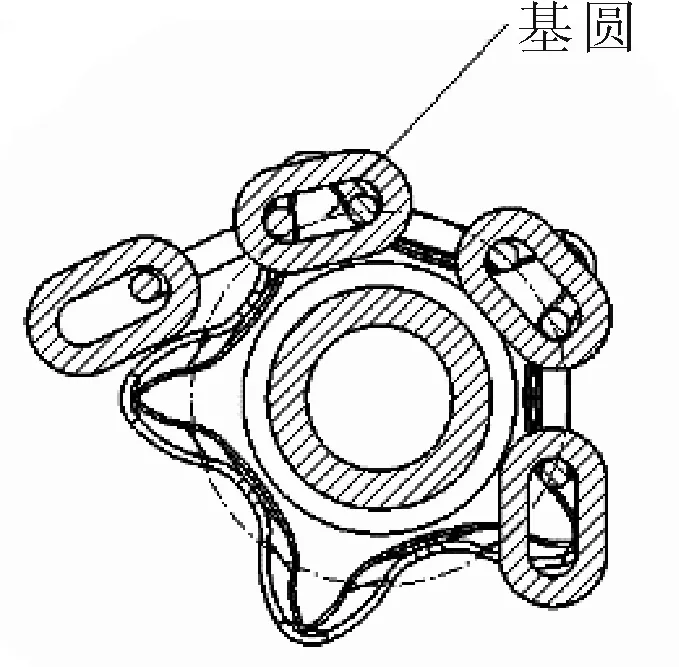
图6 锚链和锚链轮啮合过程示意

2 锚链和锚链轮啮合过程受力分析

2.1 基本参数确定

锚链和锚链轮啮合过程简化见图7。

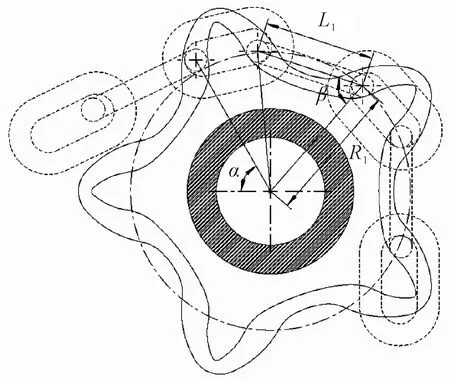
图7 锚链和锚链轮啮合过程简化

基圆半径为R1，结合国际上相关锚链轮标准，基圆半径可以用于计算锚链工作时传递最大转矩的作用半径。对于基圆半径的大小，在锚链轮标准中一般都有标注，在没有标注的情况下，根据经验公式，锚链的5齿锚链轮基圆半径为

(1)

式中：D1为锚链环的公称直径。

因此在当最大起抛锚速度为V时，锚链轮的角转速应为

(2)

如图7所示，α是锚链出锚链轮时与竖直方向的夹角，可以用于计算锚链在锚链轮中转过的总角度。

(3)

式中，D2为导链轮的公称直径；a为导链轮和锚链轮的中心距。

β为锚链环拉力和锚链环两端点连线的夹角，其大小为

(4)

式中：L1为锚链环2个端点的圆心距。

2.2 锚链环进入-啮合-离开过程受力分析

将整个锚链和锚链轮啮合过程分成3个过程，分别是:①锚链环进入锚链轮；②锚链环和锚链轮啮合；③锚链环离开锚链轮。假设锚链在锚链轮上为匀速圆周运动，其它为匀速直线运动。

1)锚链环进入锚链轮。

此时受力分析见图8，锚链环O1端只有向上的拉力T1和向下的重力G1。

图8 锚链进入锚链轮时受力分析

T1=G1

(5)

对于O2点，此时的锚链环上端点在这一瞬时已经与锚链轮刚开始发生碰撞，因此增加了支持力Fs2和摩擦力f2,此时拉力方向也发生了变化。

μFs2=f2

(6)

G2+Fs2cosb2=f2sina2+T2sinc2

(7)

T2cosc2=f2cosa2+Fs2sinb2

(8)

式中，μ为锚链轮和锚链环之间的摩擦系数。

其角度关系为

(9)

由此可以得出在这一瞬时锚链环对锚链轮的压力大小与Fs2相等，方向相反。

2)锚链在锚链轮。

此时，匀速圆周运动，合力提供向心力。

Fc3=Fc4=mω2R1

(10)

式中，m为1个锚链环的质量。

受力分析见图9。对锚链环下端点O3受力进行正交分解。

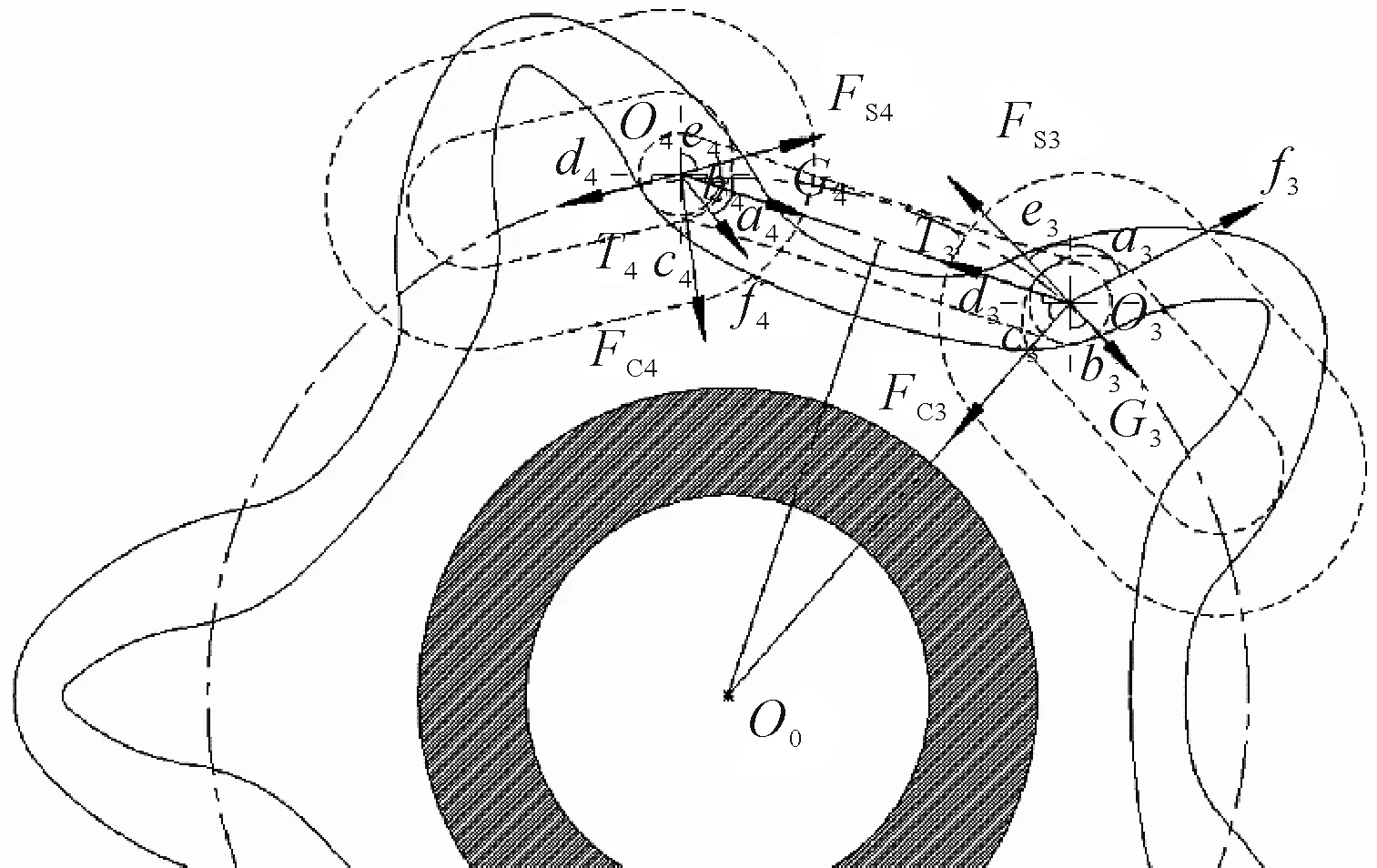
图9 锚链与锚链轮啮合时受力分析

G3sinb3+f3sina3=Fs3sine3+

T3cosd3+Fc3cosc3

(11)

G3cosb3+Fc3sinc3=T3sind3+

Fs3cose3+f3cosa3

(12)

此时角度关系为

(13)

对上端点O4受力进行正交分解。

G4cosb4+f4cosa4+Fs4sine4+

Fc4sinc4=T4cosd4

(14)

G4sinb4+f4sina4+Fc4cosc4+

T4sind4=Fs4cose4

(15)

此时角度关系为

(16)

由此可得支持力和时间的关系。值得注意的是，锚链环对锚链轮的压力与支持力大小相等，方向相反。

3)锚链环离开锚链轮。

受力分析见图10，锚链环做直线匀速运动，此时锚链环受力为

图10 锚链环离开锚链时受力分析

G5=T5

(17)

经过每个阶段的受力分析可以得出，锚链轮轮齿左右两面所受压力不相同，在已知基本参数的情况下，可得出锚链轮轮齿左右两端接触点压力与时间的函数关系为

Fs左=

(18)

(19)

3 仿真与验证

将刚柔耦合模型导入ANSYS中的瞬态分析模块，设定锚链轮和锚链材料为Q345D。设定锚链在锚链轮上进行匀速圆周运动，并且锚链轮转速为1 rad/s，锚链拉力为1 000 kN，总时长为2.5 s，计算步数为200步，接触面之间摩擦系数为0.2。对锚链进行圆周运动模型进行仿真分析得结果，为了方便观察，只输出锚链轮轮齿仿真结果。

2.5 s后轮齿等效应力云图见图11，2.5 s内轮齿最小等效应力随时间变化曲线见图12，2.5 s内接触面最大等效应力随时间变化见图13。

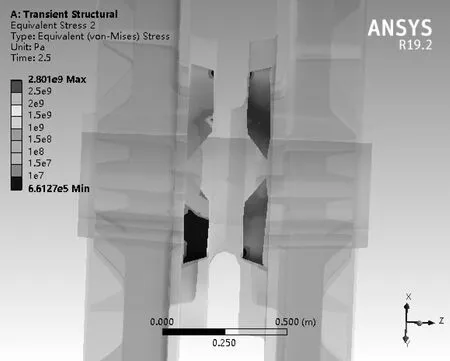
图11 2.5 s后轮齿等效应力云图

图12 轮齿最小等效应力随时间的变化

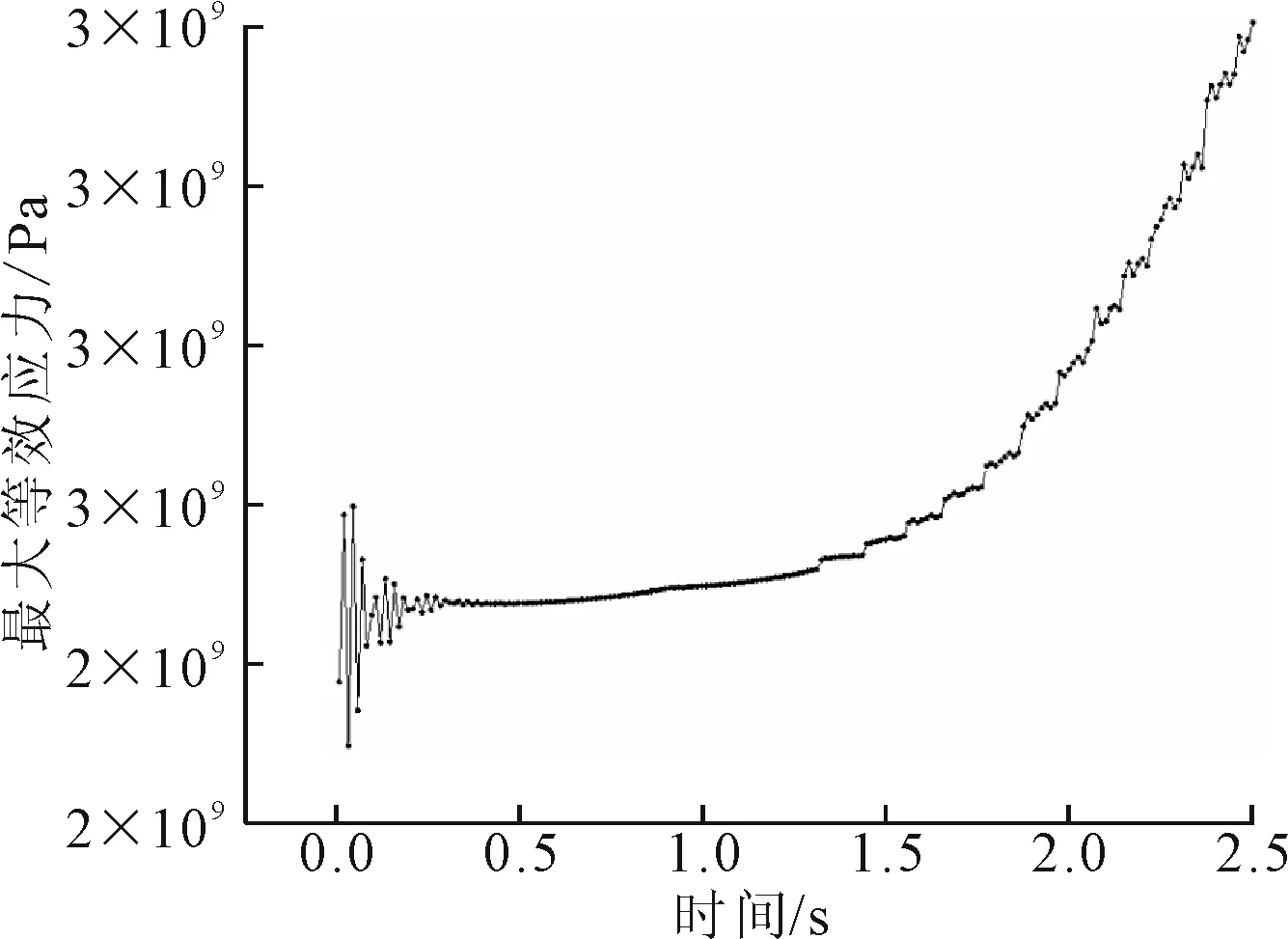
图13 轮齿最大等效应力随时间的变化

由图11可知，等效应力最大值发生在接触面边角处，等效应力最小在轮齿尖处。符合理想状态下锚链轮和锚链的啮合状况，主要受力在接触面处，齿尖基本不受力。

由图12和图13可知，在啮合过程中，一开始的碰撞导致应力变化波动比较大,随后的过程中最小应力随时间变化不大，最大应力随时间的增加而增加，且曲线斜率也逐步变大。

为了验证公式的正确性，仿真结果中2.5 s后轮齿两侧受力见图14和15，齿轮右侧Y方向受力大小为3.609×105N，齿轮左侧Y方向受力大小为6.791 4×106N；结合式(18)和式(19)算出齿轮右侧受力大小为3.857×105N，齿轮左侧受力大小为6.799 4×106N。右侧对比相对误差为6.9%，左侧对比相对误差为0.1%。表明所建立的刚柔耦合模型仿真结果和理论公式结果相近，验证了理论公式的适用性。

图14 2.5 s后轮齿右侧受力

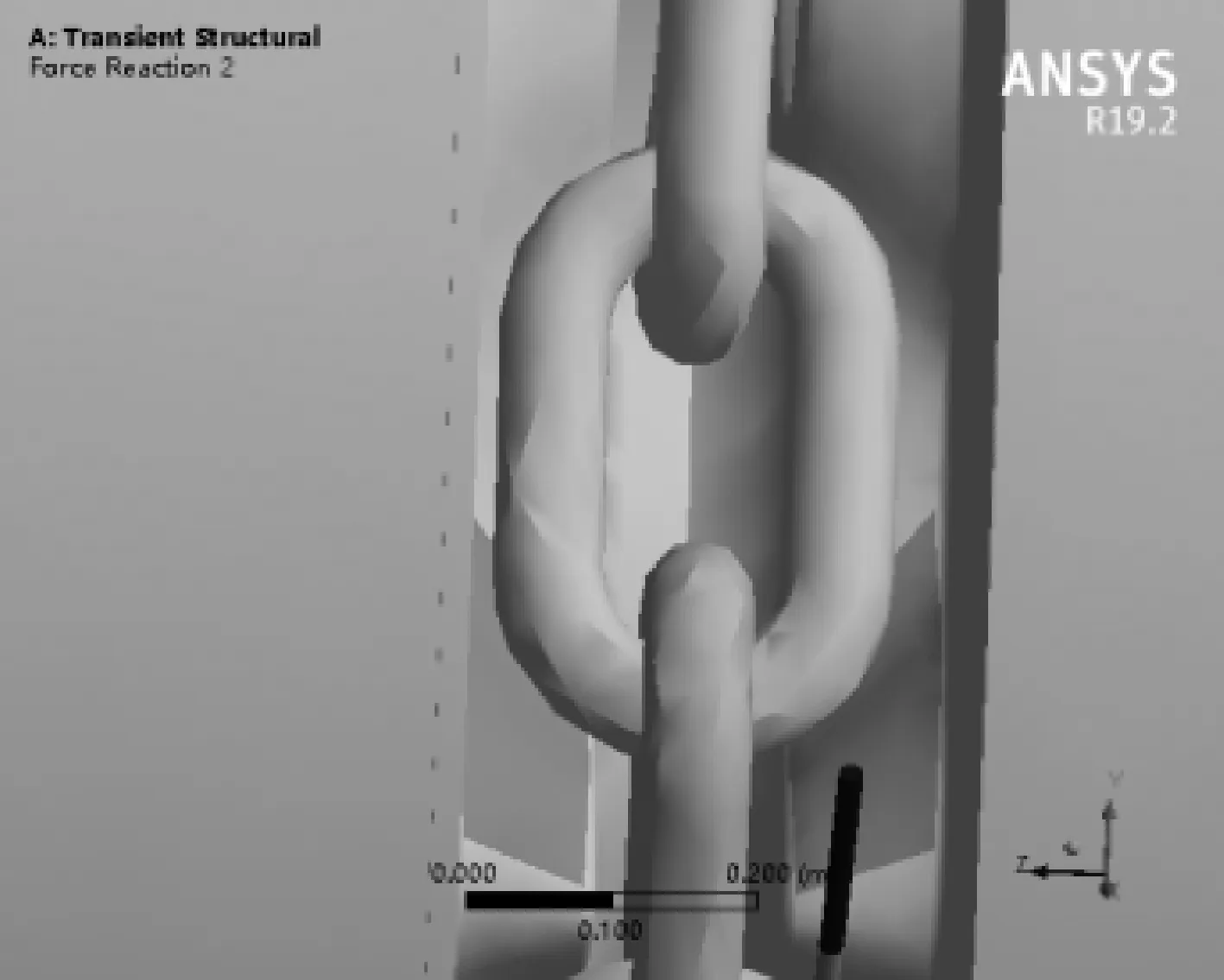
图15 2.5 s后轮齿左侧受力

为了验证锚链轮和锚链在啮合过程中的周期性，将已有的锚链轮刚柔耦合模型简化为如图16所示的锚链直线运动的刚柔耦合模型。

图16 锚链直线运动刚柔耦合模型

设定锚链轮和锚链材料为Q345D，设定锚链轮角速度为1 rad/s，总计算时长为5 s，计算步数为500。接触面平均应变与时间的关系见图17。

图17 接触面平均应变与时间的关系

由此发现锚链和锚链轮在啮合过程中，当锚链和锚链轮啮合过程平稳时，接触面的应变呈现周期性变化，且最大变形为3.818 9×10-5m。对比图13可知，锚链随着锚链轮的旋转进行圆周运动的变化规律符合锚链进行直线运动的变化规律，由此可进一步证明将锚链和锚链轮啮合过程分成3部分的可行性和准确性。

锚链直线运动刚柔耦合模型在应变最大处的应变见图18，由图18可知，应变主要发生在轮齿接触面处，最大变形为8.220 5×10-3m，且主要发生在锚链轮轮齿碰撞锚链的一侧。

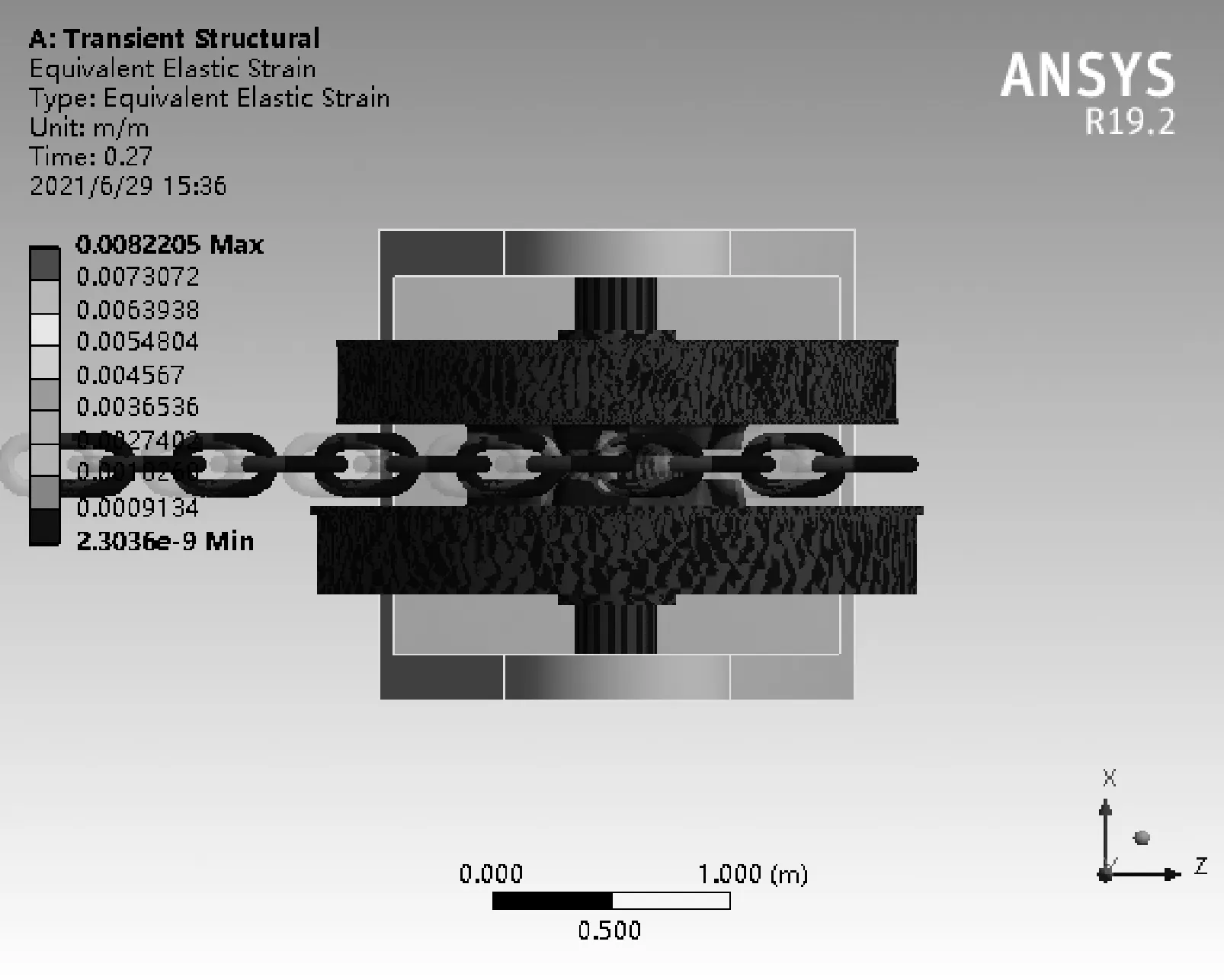
图18 0.27 s应变

4 结论

根据锚泊定位系统实际工作过程，建立了锚链和锚链轮的刚柔耦合模型，得到在理想啮合情况下，锚链环“进入-啮合-离开”锚链轮的三种状态分接触点力随时间变化关系的函数表达式。通过公式计算结果和仿真结果对比，证明了在相对误差为10%的范围内理论模型的正确性。锚链直线运动刚柔耦合模型的仿真分析表明，锚链轮和锚链在啮合过程中，锚链轮的轮齿两侧应力和应变与时间的关系呈现类正弦周期变化的规律，所设计的刚柔耦合数值模型可以应用到锚泊定位系统的动态强度校核中，能准确预测锚链和锚链轮各时间点的各项性能参数情况。理论计算和仿真结果表明，锚链和锚链轮啮合过程中锚链轮轮齿碰撞锚链侧比锚链碰撞锚链轮轮齿侧的应力应变更大，在工程应用中可以适当增加锚链轮这一侧轮齿的硬度。