相位失配弹性平板复合波导中的缺陷态∗

宋 乐 张乔木 刘 欢 樊亚仙, 陶智勇,

(1 广西无线宽带通信与信号处理重点实验室 桂林电子科技大学 桂林 541004)

(2 桂林电子科技大学海洋工程学院 北海 536000)

(3 哈尔滨工程大学物理与光电工程学院 哈尔滨 150001)

0 引言

随着声学、力学、材料科学等学科不断交叉融合，弹性波传播理论及相关研究展现出了前所未有的生机和活力，为弹性波的传播与调控提供了新的理论基础和实现手段[1−3]。与声波和电磁波不同，固体中的弹性波同时具有横波和纵波两个波矢分量，因此在弹性波调控材料以及功能结构设计上具有更强的复杂性。Zhang等[4]基于平面波展开方法，将三维固体声子晶体中的横波模式和纵波模式从混合本征模式中分离出来，并发现波导与材料的密度比会影响纵向带隙和横向带隙。Ghiba等[5]对平面波在均匀各向同性二元混合物中的传播问题进行了研究，指出平面弹性波包含纵波和横波，并且每一种波又可以分为两类，即存在着4 种不同类型的纵横波分量。Wiseman 等[6]通过三维模型评估了剪切弹性和剪切黏度的多重组合，提出利用交叉相关性的横波质点位移，能够有效地估计横波速度。与此同时，弹性波传输介质的变化，如各种天然或人工复合界面，对波传输的调控作用也渐渐成为力学中的研究热点之一[7]。

近年来，周期结构波导受到了越来越多的关注，基于周期结构的各类器件已广泛地应用于微波、电子学、集成光学及非线性光学等诸多领域[8−10]。为了调节带隙特征，更好地控制声波的传播行为，在结构中引入缺陷是一种常用的手段。Alkauskas等[11]研究了半导体中具有电活性的点缺陷处于不同变化状态时的物理特性，以及在价带最大值和最小值之间的带隙中缺陷的能级。Mertens等[12]在液晶填充的大孔径硅周期结构中发现了光子带隙，并实验证实了温度变化所导致的缺陷光谱频移。Miyashita等[13]研究了具有线缺陷的声子晶体中单缺陷模的传输特性，并对耦合缺陷模进行了研究，得到了较高的模式耦合比。对于弹性波在二维周期复合结构中的传播，引入缺陷则会改变原来的能带结构，在完美周期结构的禁带中产生一个透射峰，称为缺陷态[14]。研究表明破坏晶格的周期性，带隙内某一频率的弹性波会局域在缺陷处或者沿着缺陷传播[15]。

基于布拉格散射机制和局域共振机制，不同材料和结构周期性排列的人工复合结构会产生频域禁带。不同于声子晶体中常见的点缺陷或线缺陷，本文基于相位失配方式，通过连接两个具有相位差的正弦边界弹性波导，构建了一种具有缺陷态的波导结构，研究了弹性波禁带中透射峰的频率变化规律，并对缺陷态应力、应变的局域特性进行分析。该复合波导结构的弹性波调控特性可为声滤波器、传感器、声波导等研制提供重要参考，促进主动或智能控制器件在日常生活和工业生产中的推广。

1 弹性波导结构

板状结构是研究弹性波传播理论的常用模型。在有限元仿真软件中，建立两组分别由5 个正弦形周期单元构成的结构W1、W2并相连接，两种结构局部放大图绘制在平板波导结构上侧，如图1 所示。两个初始相位值分别为ϕ1、ϕ2；沿x轴方向的周期单元长度T是10 mm，沿y轴方向的平均厚度d为6 mm，对于z方向的尺寸参数，一般采用的是远大于厚度(d=6 mm)的尺寸，例如100 mm，以重点讨论分析二维平面内主要的低阶模式弹性波传输问题。在此模型中，垂直平面即z方向的影响有限。由正弦形边界引起的起伏参数e设置为0.6 mm；除入射边外，其余部分选择固体力学中的自由边界条件；结构材料选择铝合金；以自由三角形网格划分，并设定最大划分单元大小为1.5 mm，分析入射波在输出端变化。W1和W2结构边界表达式如下：

图1 弹性平板波导结构示意图Fig.1 Schematic diagram of the elastic plate waveguide structure

连接处相位失配如图2 所示。其中，u和v分别表示沿水平方向x和竖直方向y的位移。在具有相同周期长度和起伏参数的各向同性材质结构条件下，若W1和W2结构的初始相位相等ϕ1=ϕ2，即相位匹配，整个波导成为无缺陷的完美周期结构。反之，若ϕ1≠ϕ2，则引入了相位失配，不同失配程度实质上体现了两结构间对接处的突变程度，在这里即指初始相位差大小。对于两个周期性波导的初始相位的差异，这里通过归一化将相位差设置为∆ϕ，表达式如下：

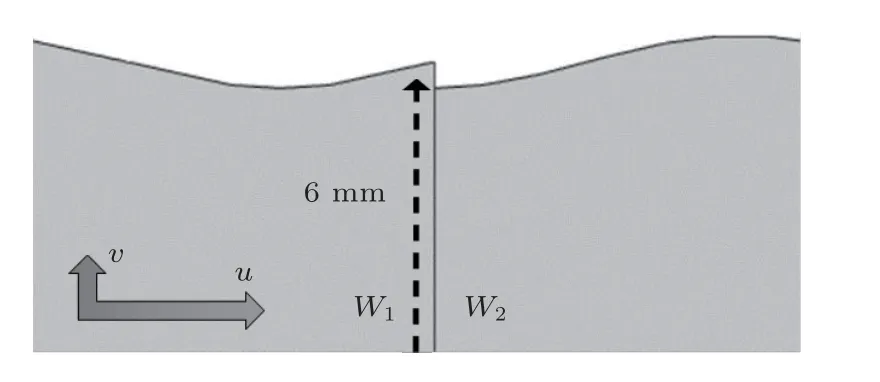
图2 对接处的相位失配Fig.2 Phase mismatch at the junction

波在周期波导中传输时，由布拉格散射引起布拉格共振则会导致频域禁带，并且布拉格共振频率与周期长度有关[16]。根据Floquet定理与边界条件，可以得到频率f与传播常数β的关系式[17]：

其中，c代表板中弹性波速度，=mπ/2(m=0,1,2,3,···)，n取整数，为空间谐波数。

在仿真中对波导左侧施加沿x轴正方向的应力以激发入射波，应力大小设置为1 N/m2，并在右侧出口处进行接收，分别用入口和出口域的平均弹性能密度PIn和POut表征入口和出口的能量大小，除波导区域外，模型的末端增加一段长度为30 mm 的完美匹配层(Perfectly matched layer,PML)作为能量吸收层[18]。这里定义透射系数Te为

根据仿真模型的参数和公式(4)、公式(5)，得到弹性波导的频带结构和透射谱，如图3 所示。结果表明，对于未引入相位差的完美周期结构，波在传播时产生了频域禁带，并且在0.46 MHz处禁带最为明显，其对应的是m=1时，由相同模式共振引起的布拉格禁带。由于公式(4)是在没有起伏时得到的色散关系，因此，实际的频带较理论预测稍稍下移。

图3 弹性波导结构的频带结构和透射谱Fig.3 Band diagram and transmission spectrum of the elastic waveguide structure

2 弹性波缺陷态

研究表明，在周期波导中引入变截面缺陷，则会造成波导的周期完整性被破坏，其谱带特征会发生变化[8]。在周期起伏弹性波导中，缺陷态的性质与缺陷和周期结构的相关参数密切相关。对于两结构W1和W2的连接处，起伏边界的相位变化扰动了起伏结构的周期波数，进而影响共振的波长和频率，产生使某一频率的波通过的缺陷态。由第1 节中频带结构和透射谱可知，在频率范围为0.44∼0.48 MHz内，波在该周期性弹性波导结构中传播会出现明显禁带。在这里，引入相位差为∆ϕ，当∆ϕ≠0时连接相位失配。在有限元仿真软件中，通过设置不同相位差值进行仿真并对入射波在周期波导结构中的传播特性进行比较，其透射谱如图4所示。波在该周期性波导结构中传播，在0.44∼0.48 MHz 频率范围内出现明显禁带，即蓝色区域。在禁带区域中发现，总会存在明显的极大值点，即透射谱中存在透射峰。而且∆ϕ=0时，即连接相位匹配，呈现为完美周期结构，没有透射峰出现。这表明弹性波周期波导中，相位失配缺陷可以导致弹性波缺陷态。

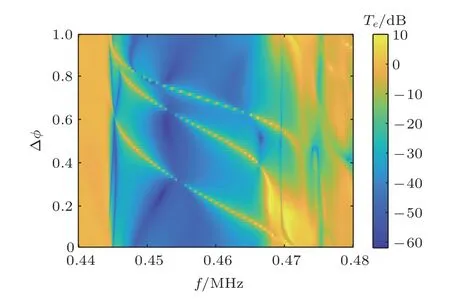
图4 透射谱随相位失配变化情况Fig.4 Transmission spectrum changes with the phase mismatch

可以看出，在归一化相位差从0 到1 的一个周期内，损耗较高的蓝色区域中分布着3 条透射率较高的黄色曲线，对应着波导结构的禁带以及禁带中的透射峰。随着相位差的变化，禁带中透射峰表现出不同的频率值，即频移现象，说明通过相位差这一结构参数可以实现对禁带中缺陷态的频率调控。

在∆ϕ=0.6附近，黄色曲线产生了向低频通带融合以及从高频通带出现的现象，这意味着相位差的变化，会导致禁带中缺陷态的消失与产生。也就是说，连接相位变化可以使禁带中的缺陷态呈现周期性频移。与此同时，更有趣的是在相位变化时，禁带中出现透射峰的数量也不同，即引入一个相位失配缺陷，可能在禁带中产生多个缺陷态。这是由于本文研究的是平板波导中的弹性波，其同时具有纵波和横波两个分量，缺陷的引入会同时改变纵波和横波的共振，从而呈现出不同的缺陷态和局域现象。这一物理现象可以为多通道声学或弹性波滤波器设计提供更多参考。

3 缺陷态局域化特征

为了进一步分析相位失配缺陷态的性质，以及弹性波缺陷态中能量的局域化现象，对其空间模场分布特征进行了研究。

3.1 应力场分布

以相位差∆ϕ分别为0.25 和0.5 为例，对蓝色区域禁带中的不同黄色曲线，即透射峰对应频率的应力场情况和弹性应变能密度分布进行数值模拟，计算结果如图5 和图6 所示。结果表明，相位失配造成的缺陷处应力分布呈现出不同的局域化特征。在这里，定义以缺陷处应力呈现极小值的缺陷态为模式1 (Mode 1)，而呈现极大值的缺陷态为模式2(Mode 2)。根据弹性波透射谱，在∆ϕ=0.25时，Mode 1 对应频率f1=457.8 kHz，Mode 2 对应频率为f2=467.9 kHz；在∆ϕ=0.5 时，Mode 1对应频率为f1=447.4 kHz，Mode 2 对应频率为f2=461.4 kHz。

图5 结构应力分布图Fig.5 Structural stress distribution diagram

图6 不同相位失配下弹性应变能密度分布情况Fig.6 Distribution of elastic strain energy density with different phase mismatches

通过对比两种不同缺陷模式可知，应力场能量主要集中在缺陷两侧的周期结构中，且沿波导两侧逐渐减弱。不同的是，Mode 1 的应力场分布在板中沿中心水平轴分布着极大值；而Mode 2 的应力场分布中，除能量在板中沿中心水平轴分布着极大值的特征以外，在板的厚度方向上也出现了极大值，并且两种情况交替出现。这种现象表明不同频率下的缺陷态在应力场局域化特征上存在差异，并且这种差异并不是由相位差的变化引起的，相同相位差却引入了不同的缺陷态，随频率不同而导致应力分布不同。因此，通过选择不同模式的缺陷态可以调控弹性板应力场的局域化特征。

3.2 空间位移场分布

不同缺陷态会导致应力局域化特征不同，相应的空间位移场分布也必然不同。分别对不同模式缺陷态的水平位移分量和竖直位移分量进行了模拟，结果如图7和图8所示。

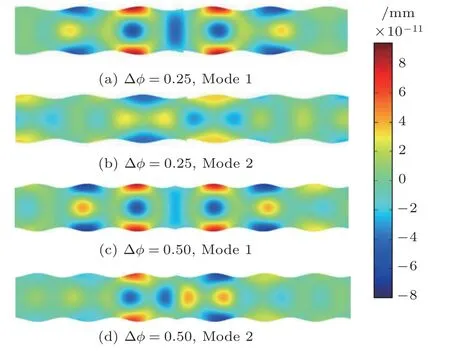
图7 位移场水平分量分布图Fig.7 Horizontal component distribution of displacement fields

图8 位移场竖直分量分布图Fig.8 Vertical component distribution of displacement fields

由图7 可以看出，位移场水平分量在周期波导结构中具有对称和反对称分布两种特征。Mode 1的位移场分布表现为对称特征：相位失配缺陷处是极小值，能量主要局域在相邻的两个不同相位的周期单元中心，且关于缺陷中心呈现对称分布特征。Mode 2的位移场分布表现为反对称特征：以相位失配缺陷处为中心，左右两侧分布着相反的极值情况，即呈现出反对称分布特征。

与位移场水平分量情况相似，位移场竖直分量在周期波导中也存在着对称与反对称分布特征，如图8 所示。其中Mode 1 对应的场分布表现为关于连接处呈反对称分布；Mode 2对应的场分布表现为关于连接处呈对称分布。这种分布特征恰好与位移场水平分量情况相反，这表明两种不同缺陷态可以导致完全相反的位移场分布特性。因此，不同模式下的缺陷态也可以用来调控弹性板位移场的分布。

为了更清楚地说明相位失配引入的弹性波缺陷态特征，将不同缺陷模式的空间场分布特征汇总于表1，并给出了两种不同缺陷模式所对应的频率随相位差变化的关系曲线，如图9 所示。可以看出，在Mode 1 与Mode 2 随相位差变化而产生频移过程中，呈现出同一能量局域化特征的Mode 1 从高频向低频移动，当相位差大于0.5时，Mode 1从禁带下边缘消失，而后重新从禁带上边缘出现；而呈现与Mode 1 相反局域化特征的Mode 2，从高频禁带边缘开始，随相位差的增大逐渐向低频移动，当相位差变化一周期后，消失于低频禁带沿。也就是说，在一个相位差变化周期内，Mode 2产生了一个从高频向低频移动的过程，Mode l 却产生了两个周期的频移变化过程。这表明禁带中的透射峰数目是由两个缺陷模式频移的周期不同造成的。

表1 不同缺陷态的应力及位移场情况Table 1 Stress and displacement fields of different defect states

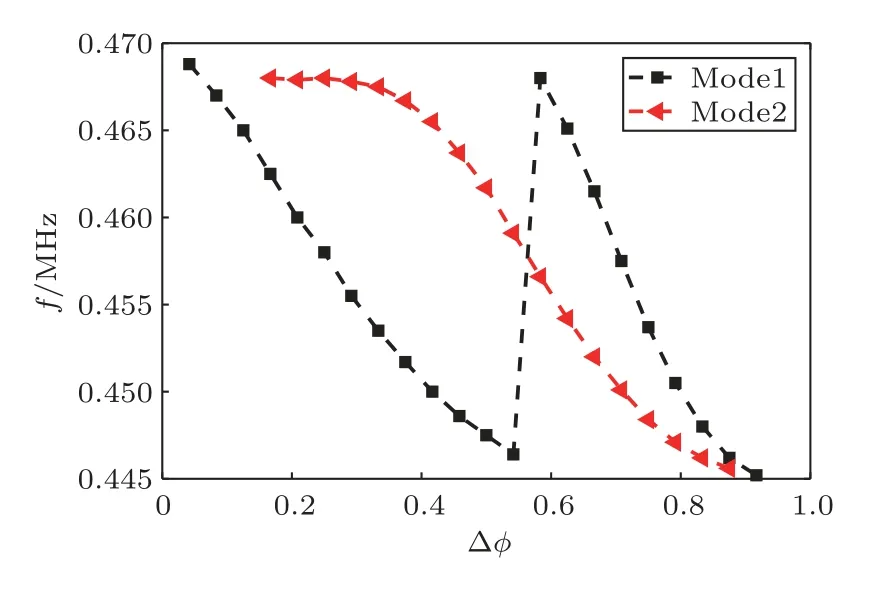
图9 不同缺陷态的频率随相位差变化Fig.9 Frequency of different defect states vs the phase difference

4 结论

本文设计了一种基于周期起伏结构的弹性平板波导，并在波导结构中引入了相位失配产生的缺陷，对透射谱禁带中产生的缺陷态特征进行了研究。结论如下：

(1) 周期起伏弹性板中会形成弹性波禁带，引入相位失配缺陷可以观察到禁带中的缺陷模透射峰，且透射峰随相位差变化而发生频移。不仅如此，禁带中透射峰的数目也受相位差大小影响。研究表明边界起伏和相位连接条件都会影响弹性板的谱带特性，不同的相位失配程度可以造成不同特征的弹性波频谱，并且形成缺陷态的数目也不同。

(2) 对缺陷处的能量局域化现象进行了进一步的分析，结果表明不同缺陷态的应力场以及空间位移场分布具有不同的特征。研究表明，不同频率的缺陷态对应的场分量存在不同的能量局域特征，分别呈现出对称及反对称规律。

(3) 对于两种不同缺陷模式，归纳了相位差与模式之间的频率分布，揭示了不同缺陷模式具有频移周期不同的特征。

由于弹性波在波导内具有横波和纵波两种类型，除了它们与结构的作用外，两者之间也存在相互转换。所以即使结构中只引入一个相位失配缺陷，禁带中也可能出现两个特性不同的透射峰。由于产生缺陷态的频率与结构尺寸密切相关，等比例放大结构参数，缺陷态频率也会随之降低。即便不增大结构尺寸，目前的工艺也完全可以精确加工相关的弹性薄板。进一步研制高精度的弹性波检测系统，则可以对本文提出的相位失配缺陷态调控机理进行实验验证。利用光学干涉方法高精度检测弹性波模式[19]，将成为有效手段。总之，本文提出的弹性波缺陷态调控方法不仅有利于波导的带隙分析以及弹性波应力、应变场调控研究，也为声学滤波、缺陷态特征模式分析、结构振动噪声衰减等声传播控制领域提供重要参考和解决方案。