深海远程正交频分复用水声通信簇约束的分布式压缩感知信道估计∗

王悦悦 王海斌 台玉朋 汪 俊 王光旭

(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

在深海远程水声通信中，信道带宽窄，频谱资源十分有限[1]。正交频分复用(Orthogonal frequency division multiplexing,OFDM)调制技术通过子载波并行叠加的方式进行信息传输，有望提高深海远程水声通信的频带利用率[2]。然而，由于海底、海面边界以及水体的不均匀性对声传播的影响，远程通信的水声信道往往呈现出远比无线信道恶劣的强多径、长时延扩展特性，多径时延扩展通常可达几百毫秒至数秒[3−4]，这也导致深海远程OFDM水声通信需要面对长时延带来的严重频率选择性衰落问题，而精确的信道估计是有效补偿信道衰落的前提，也是深海远程OFDM水声通信中的难点问题。

水声信道是典型的稀疏信道，因而其估计问题可转换成稀疏信道的重建问题。近年来得到广泛研究的压缩感知(Compressive sensing,CS)理论可以用于提高OFDM 信道估计性能[5]，该理论在2006年由Donoho 提出[6]，随后被引入到水声通信的信道估计中，而在2010 年，Berger 等将其用于基于导频的OFDM水声通信系统信道估计中[7]，验证了基于基追踪(Basis pursuit,BP)和正交匹配追踪(Orthogonal matching pursuit,OMP)的CS 算法相较于传统最小二乘(Least square,LS)算法在OFDM信道估计中的优势。

但是，OMP 信道估计算法本质上是利用导频处的接收符号与字典原子匹配相关来进行信道重构的过程，需要插入与信道长度相匹配的导频符号数目，来保证估计性能。而对于长时延扩展的水声信道，这意味着需要较高的导频密度，导频开销增加则会导致频谱利用率降低。

考虑到对于缓变水声信道，在一定时间内接收到的OFDM 数据块之间，其水声信道多径的稀疏结构具有一定相关性，这种信道的时域相关性为进一步改善长时延水声信道的CS 估计性能提供了可能。2009 年，Baron 等[8−9]针对多个信号稀疏性具有相关性的现象提出了分布式压缩感知(Distributed compressed sensing,DCS)理论，通过利用多个信号的共同稀疏性进行联合重构可进一步提高稀疏重建性能，并针对典型分布式稀疏信号提出JSM2(Joint Sparsity Model 2)模型，模型中各个信号间具有相同的稀疏支撑集，但不同信号的非零系数不同。针对上述信号特性，可以利用同步正交匹配追踪(Simultaneous orthogonal matching pursuit,SOMP)算法，来解决该信号的稀疏恢复问题[10−11]。2016 年，周跃海等[12−13]研究了DCS 理论在水声信道估计中的应用，并且将稀疏OFDM信道估计问题在DCS 的框架下转换成JSM2 模型下具有相同支撑集的联合稀疏恢复问题[14]，利用数据块与数据块多径稀疏特性的相关性进行联合稀疏恢复信道估计，从而达到提高稀疏信道估计性能的目的。近年来，Qiao 等[15−16]还探索了利用稀疏贝叶斯的信道估计方法进行联合信道估计的可行性，利用插入的导频符号进行块间联合稀疏贝叶斯信道估计，同样验证了联合多数据块进行信道估计的性能优势。

深海远程水声信道在一定时间内具有相关性，符合JSM2 中的信号联合稀疏模型，因此能够利用数据块间的联合稀疏特性进行基于SOMP 的DCS估计，同时，考虑到深海远距离水声通信空间跨度大，信道呈现簇状分布[17−18]，并且在多个相邻数据块时间内，信道簇结构较为稳定，即信道能量稳定聚集在少部分簇区域中，充分利用簇特性信息将能够进一步提升稀疏信道估计精度。传统的DCS 算法未能考虑深海长时延信道的簇稳定特性，为此，本文提出一种簇约束的DCS(Cluster restricted DCS,CR-DCS)信道估计方法，首先，利用前后导码信号进行信道簇区域的识别，并根据簇起始终止位置构建簇区域约束矩阵；其次，在传统JSM2 模型的基础上，根据约束矩阵构建簇约束的联合信道稀疏模型，该模型通过矩阵乘的方式限制待估计信道簇区域所在位置，并通过该模型推导出簇约束联合字典矩阵；最后，采用簇约束的SOMP 算法求解信道联合稀疏优化问题。与传统的DCS 信道估计算法相比，该方法同时利用了深海远程信道的缓变特性和簇区域稳定性，提高了信道估计精度，从而降低通信误码率。

1 系统模型

在零后缀(ZP)的OFDM 信号结构中，令T表示OFDM 符号时间，Tg表示保护间隔并且Tg的取值大于最大信道时延，一个OFDM 块的总时间为T′=T+Tg，定义dl为第l个子载波上待调制的符号，d=[d1,d2,···,dl]为子载波符号构成的向量，L个子载波可用于调制数据符号或是导频符号。单个数据块的时域发送信号的离散形式可由发送符号经过逆傅里叶变换得到：

其中，F−1(·)表示离散傅里叶逆变换函数。在多个数据块构成的时域信号矩阵的每一列插入保护间隔，并进行并串变换，构成一帧OFDM信号，在信号的前后两端分别插入前后导码，用于信道同步与多普勒估计以及簇区域信息的确定。

假设信道在一个OFDM 数据块时间内信道缓慢变化，且所有路径都有相同的多普勒扩展因子a，对应水声信道模型为

其中，K代表信道离散路径个数，即信道稀疏度，Ak和τk分别代表第k径的信道幅度和对应时延，δ()表示狄拉克函数。

在接收端，利用前后导码对多普勒扩展因子进行粗估计[19]，并通过插值的方式进行补偿。经串并变换进行数据块的分离，然后经OFDM解调将时域数据块的信号转换成频域接收符号形式，表示为

其中，w ∈CL×1代表频域噪声，z ∈CL×1为频域接收符号，H ∈CL×1为信道频域响应。

在进行块独立的信道估计时，发送符号中插入的导频信息已知，本文中导频结构为随机插入的方式，可以利用导频处的发送接收符号进行信道估计。导频处发送和接收符号的关系如下：

式(4)中，下标()p代表导频，zp∈CLp×1，Lp为导频子载波数，zp代表导频处符号观测所得向量，Hp∈CLp×1，h ∈CNde×1，Nde为离散信道采样长度，Hp为时域信道响应h在导频对应频点处的离散傅里叶变换，wp为与噪声有关的项。

由于水声信道具有稀疏性，即向量h中只有少量元素不为零，故h的估计问题可以转换为稀疏信号的恢复问题。定义Ψ=diag(dp)F为字典矩阵，将式(4)写成基于字典的矩阵表达式为

其中，zp为观测向量，h为待估计的稀疏向量，Ψ=[ψ0,ψ1,···,ψNde−1]，它的列向量ψi为第i个字典原子，ψi长度等于导频数目Lp，字典矩阵的大小为Lp×Nde。

采用CS 算法进行OFDM 稀疏信道恢复时，通过时延划分构造出字典矩阵Ψ，并将导频处的信道响应作为观测值，通过求解式(6)中带约束的优化问题来利用少量字典元素重构稀疏时域信道响应h：

其中，δ为与噪声有关的一个参量，在CS 的理论框架下，该优化方程可以采用OMP 算法进行稀疏重构，OMP 算法利用贪婪思想在每次迭代选择一个局部最优解来逐步逼近原始信号，算法步骤中包含Gram-Schmidt 正交化的处理，保证了每次迭代的最优性。但当信道h的多径时延扩展较大时，采用OMP 方法进行稀疏重构时需要较多的导频来确保期望信号和接收信号具有较好的相关性，导致频谱效率降低。而SOMP算法则利用了多个数据块的信道稀疏相关性，通过多个数据块联合确定稀疏支撑集，并独立地求解数据块确定各自的多途幅度，能够在OMP 算法的基础上，利用多数据块的联合增益，提升估计性能。

2 CR-DCS信道估计

CR-DCS 信道估计方法利用了信道在一定时间内的相关性以及信道呈较稳定簇状分布的特性，能够有效提高估计精度。方法进行信道估计的具体流程如图1 所示，方法主要包含3 个部分：第一部分包括分别对前后导码进行簇区域位置检测识别，并生成簇区域约束矩阵；第二部分包括建立基于JSM 的簇约束信道联合稀疏模型，并利用该模型推导出簇约束的联合字典矩阵；第三部分通过簇约束的OMP 算法求解稀疏信道估计的优化方程，得到各个数据块的时域信道响应估计结果。

图1 CR-DCS 信道估计方法流程图Fig.1 Flowchart of cluster-constrained distributed compressed sensing channel estimation method

2.1 信道簇区域检测

信道的簇状区域的位置通过接收端已知的前后导码来确定，前后导码分别在OFDM帧结构的最前面和最后面，通常为多普勒不敏感波形。以前导码信号的簇检测过程为例，将前导码信号当作本地波形x(t)，定义H0为无有用信号假设，H1为有有用信号假设，对本地已知前导码信号和输入接收信号y(t)进行匹配滤波(Matched filtering,MF)后的结果可用公式表示为

其中，rxx(t)是x(t)的自相关函数，rxη(t)是x(t)和环境噪声η(t)和相关函数。定义rMF[n]为rMF(t)的离散采样值。假定相关样值rxη[n]服从高斯分布，即rxη[n]∼CN(0,)。定义归一化滤波器输出的平方为

它服从在H0下的非中心的χ2分布。为了适应水声信道多径簇状分布的特点，可以使用基于cMF[n]的对数似然比(Log-likelihood ratio,LLR)累加和的序列检测器进行信道簇检测，cMF[n]的LLR 用公式表示为

为了简化LLR 中归一化匹配滤波器的概率密度函数计算，对于非中心的χ2分布信号cMF[n]，将其进行本地最佳非线性化[20]后得到

其中，b是错误报警的抑制偏差。采用声呐和雷达系统中常用的Page 序列检测器[21]进行簇检测，其LLR的Page累加和定义为

根据式(11)中的迭代关系对每个n对应的TPage[n]进行迭代计算，并在迭代过程中进行簇识别，识别规则为

在TPage满足式(12)中的条件(1)时，记录簇起始位置=n，迭代继续；在TPage满足式(12)中的条件(2)时，记录簇结束位置=n，更新簇索引，迭代继续。对所有的n迭代结束后输出各簇的起始和终止位置参数，c为簇索引，Nc为簇个数。

同样对后导码进行簇检测，可以得到后导码对应信道各簇的起始和终止位置参数,c ∈[1,Nc]，信道最终簇区域位置为前后导码对应信道簇区域的并集，即各簇的起始位置由前后导码对应簇起始位置中的较小值确定，而终止位置由前后导码对应簇终止位置中的较大值确定：

进一步可以得到簇区域约束矩阵：

簇区域约束矩阵Φ ∈CNde×Nde为对角矩阵，其对角元素ϕi的取值满足

即簇区域约束矩阵在信道存在簇状多途的区域对应的对角元素为1，其余为0。

2.2 簇约束的联合字典矩阵构建

在联合稀疏模型(JSM2)下，N个数据块对应的信道冲激响应向量hi(i ∈[1,N])具有联合稀疏性，即每个hi中少数不为零的抽头所在位置均相同，但不同信道之间每个抽头对应的多径幅度不同，N个数据块的联合信道响应模型可表示为

式(16)中，hi ∈CNde×1，为第i个数据块对应的时域信道响应向量，Ω表示N个信道共同稀疏支撑集对应的路径矩阵，Ω ∈CNde×K，矩阵列数K对应信道的共同稀疏度，路径矩阵中的每一列对应一个多径，在各个列向量中，各多径的时延对应位置处元素为1，其余部分为0，ξi ∈CK×1为第i个数据块的多径系数构成的向量，对于不同的i，该路径系数可以有不同的取值。

在此信道模型基础上引入式(15)中的簇区域约束信息，构建簇约束的联合信道稀疏模型，该模型中各个数据块在簇区域约束下的信道冲激响应为

在簇约束的联合信道稀疏模型下，将式(5)中导频子载波处的信号输入输出关系从单数据块扩展到N个数据块可以得到

定义式(18)中的Λ ∈CNLp×NNde为簇约束的联合字典矩阵，∈CNNde×1为联合接收导频符号向量，∈CNNde×1为联合信道向量，∈CNNde×1为与噪声有关的向量。在联合字典矩阵中，Ψi ∈CLp×Nde(i ∈[1,N])为单个数据块的字典矩阵，不同数据块的字典矩阵Ψi(i ∈[1,N])中的导频子载波位置集合可以不同。事实上，在导频插入密度相对信道时延较低时，各数据块之间互不相同的导频位置能够在CS 匹配相关的过程中提供更全面的子载波响应信息，从而使得匹配相关的结果更加准确。因此，本文方法中，导频子载波采用各数据块相异的随机插入方式。

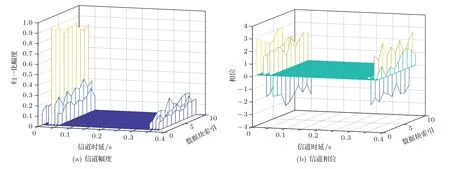
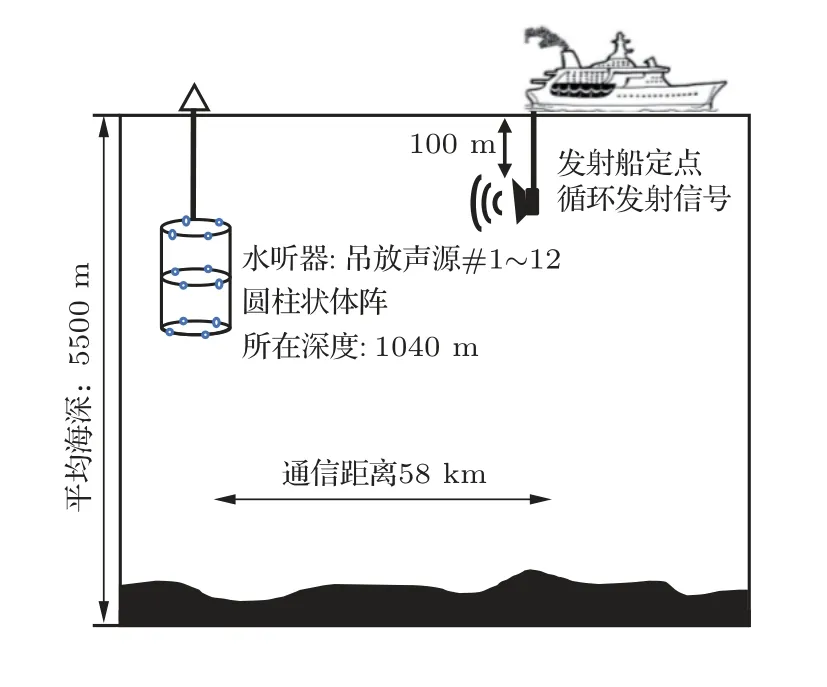
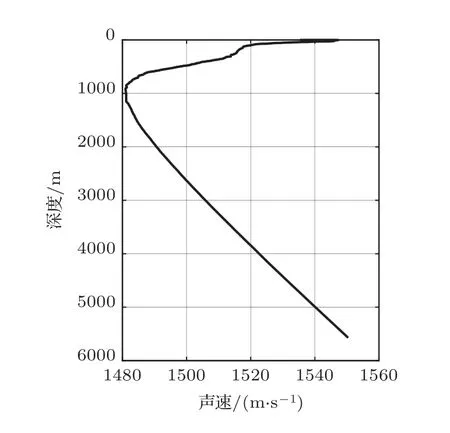
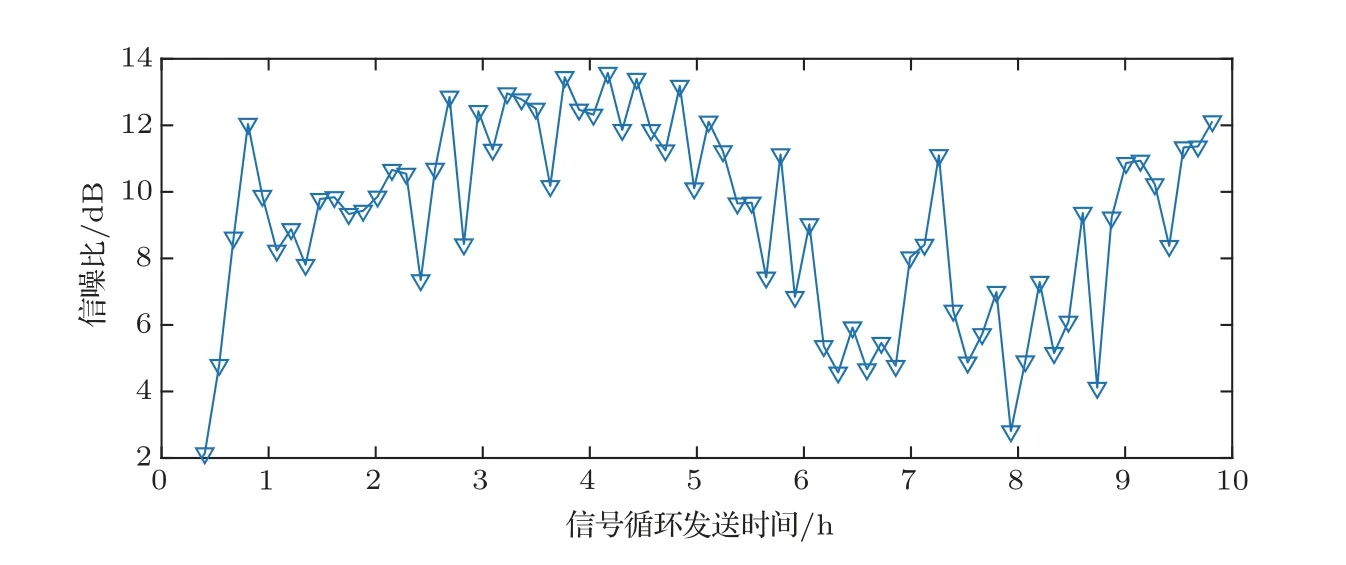
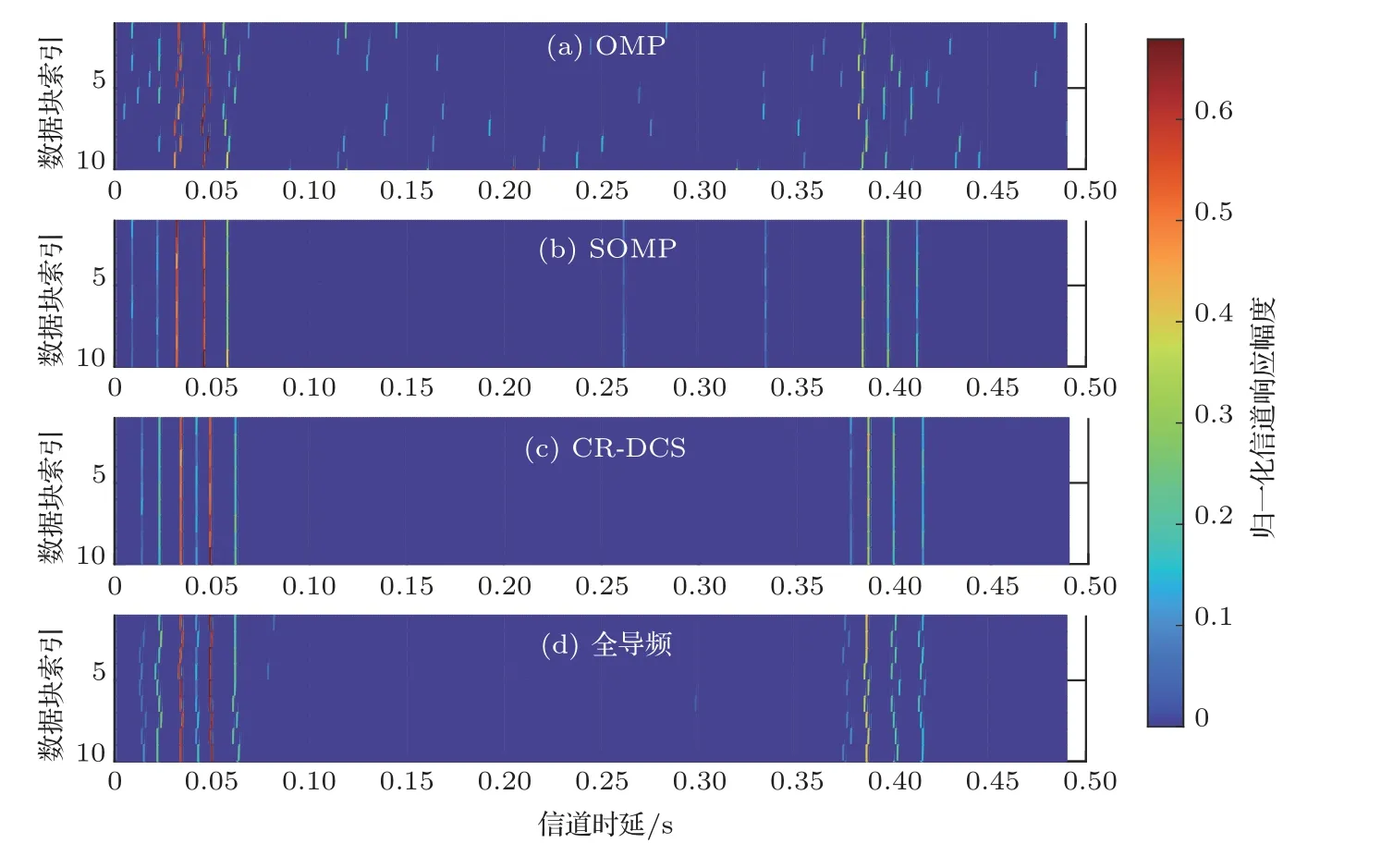
从N个数据块输入输出关系推导结果来看，本文所提方法中的簇约束的联合字典矩阵Λ与SOMP 算法中的联合字典矩阵的区别在于引入了簇约束矩阵Φ，在Φ作用下，联合字典矩阵Λ中在簇对应位置字典原子(ψi,ns

2.3 簇约束的OMP算法求解

利用DCS 的思想可以利用式(18)中的水声信道进行联合稀疏恢复，联合N个数据块进行联合信道向量的稀疏重构，对应优化问题表示为

式(19)中的优化问题可以利用簇约束的SOMP 算法来求解，算法的具体实现步骤如下：

输入：N个OFDM 数据块的簇约束联合字典原子矩阵Λ；N个OFDM 数据块的解调符号∈CLpN×1；最大迭代次数K；残差门限δ。

第一步：分别选取字典矩阵Λ中第i块对应的子矩阵的ΦΨi和残差做内积，并求出N个数据块对应的内积和，计算内积和的最大位置mλ，并保存各子矩阵位置mλ对应的字典原子ψmλ,λ；

第二步：采用LS 法分别计算每个数据块对应的多径系数并更新残差；

采用CR-DCS 估计方法对水声信道进行估计时，利用了多个数据块信道的共同稀疏性，在SOMP算法迭代中对数据块间多径位置相同的部分进行叠加，联合确定多径稀疏解的位置，提高信道多径重构准确度，并引入簇区域约束矩阵，确定了有效字典原子的范围，降低了噪声区域对估计结果的影响，进一步提高了估计精度。

3 仿真和实验验证

对所提方法的性能分别进行了仿真和实验验证，对比分析了3 种方法下的信道估计性能，分别为基于OMP 的CS 信道估计方法[6]、基于SOMP 的DCS 信道估计方法[8]和本文所提出的CR-DCS 信道估计方法。在信道估计时，OMP为块独立的信道估计结果，SOMP和CR-DCS均为将10个数据块进行联合同步估计的结果。

3.1 仿真结果

发射信号采用4-QAM 的OFDM 调制方式，符号时长2.56 s，保护间隔2 s，一帧OFDM 发射信号共包含10 个OFDM 数据块，每个数据块的调制信号中包含256个子载波，其中，导频子载波插入密度为1/8，对应导频子载波数32个，导频子载波随机插入在256 个子载波中，剩余的子载波用作数据子载波。发射信号具体参数见表1。

表1 仿真所用发射信号参数Table 1 Transmit signal parameters used in the simulation

仿真所用信道模型来自实测数据提取的水声信道，信道的平均功率延时分布的幅度(单位：dB)和对应的时延τ(单位：s)参数为

仿真信道多途模型呈现明显的两簇结构，信道最大时延扩展为0.37 s，信道具有稀疏结构，稀疏度为9。在该功率延时分布下，信道的时变遵循JMS2模型，即信道在不同数据块间具有相同的抽头时延和不同的抽头幅度。每一个数据块对应的各抽头幅度平均值为，抽头幅度在各数据块的变化方差为0.1，每一个数据块对应各抽头的相位为[−π,π]的随机值，抽头相位在数据块之间的变化方差为π/4。上述参数下生成的时变信道如图2所示。

图2 仿真所用时变信道的幅度和相位Fig.2 Amplitude and phase of the time-varying channel used in the simulation

在图2 中的仿真时变信道作用下，3 种方法误码率性能曲线如图5 所示。从图5 中可以看出，在1/8 的导频密度下，逐块的OMP 算法估计性能较差；而多数据块联合的SOMP 算法能够明显提升误码率性能；在此基础上，考虑信道簇区域信息后，CR-DCS 算法能够将误码率性能进一步提升，更加接近完全CSI 已知时的误码率性能，表明了本文所提方法相对于传统SOMP算法的性能优势。

图5 仿真信道下不同方法的误码率对比Fig.5 Comparison of bit error rates of different methods under simulated channels

3.2 实验结果

在深海海域进行了定点水声通信试验，发射船定点发射，接收阵为12 阵元的圆柱状体阵，位于距海面约1040 m 处，收发距离约为58 km，发射站点到接收站点之间的平均海深为5500 m，信号循环发送，共发送74 轮信号，相邻两个信号的发送间隔为484 s，总的信号发送时间为9.95 h。具体通信实验环境信息如图6 所示，水文测量获取的接收站点附近声速剖面如图7 所示，从图7 中可以看出，圆柱状体阵所在位置接近声道轴处。

图6 深海海域远程水声通信实验环境信息Fig.6 Experimental environment information of remote underwater acoustic communication in deep sea area

图7 接收阵附近声速剖面图Fig.7 Profile of sound velocity near the receiving array

发射信号为带宽为100 Hz的低频OFDM信号，带内平均声源级为165 dB。信号采用4 阶的QAM调制方式，发射信号具体参数见表2。

表2 实验OFDM 发射信号参数Table 2 Transmit signal parameter value

发射信号的符号时间长度2.56 s，保护间隔ZP的时长为0.44 s，两者构成一个3 s 的数据块，在一帧信号中，共有10 个数据块，数据块前后各有一个5 s长的线性调频(Linear frequency modulation,LFM)信号，分别为前后导码，用于信号同步、多普勒估计和信道簇区域检测。发射信号总时长40 s，在1/8 导频插入密度下，100 Hz 带宽为(B)的M阶(M=4)星座图映射信号对应的无编码数据传输速率为

根据文献[19]中的方法，利用前后导码的相关最大值对应的时间差进行多普勒因子的估计，并通过插值方法进行多普勒补偿，选用声速为1500 m/s时，接收信号的多普勒速度估计结果随时间变化的曲线如图8 所示，每一个信号对应的多普勒速度值为12个圆柱状体阵阵元取平均的结果。从图8中可以看出，尽管发射接收都为定点装置，信号依旧受到多普勒效应的影响。产生多普勒效应的主要因素有水体起伏、接收阵摆动等，多普勒速度整体处于较低的水平，在−0.6∼0.2 m/s范围波动，对应的频率偏移范围为−0.12∼0.04 Hz，并且在2∼5 h 时间区间有一段较为平稳的时期，对应多普勒速度接近0。

图8 阵元平均后的接收信号估计多普勒速度-时间曲线(声速1500 m/s)Fig.8 Doppler velocity-time curve of received signals estimated after array element averaging(sound velocity: 1500 m/s)

得到OFDM 解调后的频域接收符号后，利用数据子载波和空子载波处平均能量进行接收SNR的估计。图9 给出了循环发送期间各个接收信号的SNR随时间变化的曲线，图9 中同样为12个圆柱状体阵阵元取平均的结果。可以看出接收信号整体SNR 偏低，大致处于4∼12 dB 区间，且在信号发射时长为2∼5 h的区间，即图8中的多普勒速度靠近0的时间段，SNR处于较高的水平，接近12 dB。

图9 阵元平均后的接收信号信噪比-时间曲线Fig.9 SNR-time curve of received signal after array element averaging

使用Page 成簇算法分别对降至基带的前后导码信号进行簇检测，在计算累加和之前，将cMF[n]的最大功率归一化，将式(10)中错误报警的抑制偏差b取值为0.004，门限分别取值为0.2和0.4。为方便理解，将cMF[n]和TPage[n]中的序列索引变量n转化为时间变量t，二者转化关系为t=n/fs，其中，fs为离散信号的采样率。

采用Page 成簇算法对单个信号进行簇检测，归一化滤波器输出随时间变化的结果cMF(t)以及LLR的Page累加和TPage[t]的结果如图10所示。从图10(a) 和图10(b)中可以看出，前后导码处对应的信道均为明显的两簇结构，第一簇能量明显高于第二簇，两簇之间的时延差约为0.37 s。图10(c)、图10(d)分别为前后导码LLR 的Page 累加和结果，可以看出，Page 成簇算法通过对LLR 累加求和能快速检测信号序列中的变化，通过设定门限，限制累加和的最大值，能在簇结束时进行快速反应。前后导码信号输出的各簇起始和终止位置如表3所示。

表3 前后导码各簇起始和终止位置检测结果(单位：s)Table 3 The detection results of the start and end positions of each cluster of the preamble and postamble (unit: s)

图10 单个信号的前后导码簇区域检测结果Fig.10 Preamble and postamble cluster region detection results of a single signal

从表3 中可以看出，前导码和后导码的各簇起始和终止位置较为接近，表明在10个数据块的时间内，信道的簇区域基本稳定。用于后续信道估计的簇区域信息为前后导码检测结果的并集，即第一簇起始终止位置：{0.0120,0.0763}，第二簇起始终止位置：{0.3693,0.4343}。

为了评估不同方法在不同深度和距离条件下的信道估计误差，引入符号均方误差(S-MSE)这一性能指标进行分析和对比，S-MSE的定义为估计信道作用于发射符号后与实际接收符号之间的归一化均方误差，其中为信道频域响应估计值的离散形式，Xl为归一化发射符号，Yl为解调后归一化接收符号。符号误差越小，表明所估信道与实际信道接近程度越高，估计性能越好。

对12个阵元取平均后，74轮发射信号对应的SMSE 曲线如图11 所示，从图11 中可以看出，OMP对应的S-MSE 性能较差，主要原因为用于信道估计的导频数目未能满足信道长度需求；而SOMP 与OMP 相比性能改善明显，改善的原因来自于多个数据块之间的联合增益，但依旧存在性能不稳定的情况；而CR-DCS 方法在加入了簇区域限制后，能够在SOMP 方法的基础上，进一步降低符号均方误差、提升估计性能，并且与SOMP 方法相比，CR-DCS方法具有较强的稳定性。

图11 不同信道估计方法下12 阵元平均后的S-MSE 曲线Fig.11 Averaged S-MSE curves of 12 array elements under different channel estimation methods

选取其中一个信号的信道估计结果进行分析，在进行接收信号处理后，得到所估信道时域冲激响应结果见图12，图12(a)∼(c)分别为OMP、SOMP和CR-DCS 三种方法对应的估计结果，而图12(d)为将全部子载波视为导频时采用OMP 方法得到的信道估计结果。从图12(c)和图12(d)的估计结果可以看出，信道时延扩展约为0.4 s，呈现出较为明显的两簇结构，且第一簇能量更强。对比子图12(a)和图12(b)可知，块独立的OMP方法所估信道在两簇之间存在较多的非零项，且第二簇多途由于能量较低基本被淹没在噪声中，而SOMP 方法则通过利用块间的联合稀疏特性进行估计，明显降低两簇之间的非零项。通过对比图12(b)、图12(c)和图12(d)可知，采用SOMP 方法估计信道时，部分强度较弱的路径仍然会被噪声淹没，导致出现多途估计误差项；而CR-DCS 方法则能够在簇区域信息的约束下，确保信道能量较好地集中在簇所在区域，更加接近全导频估计信道的能量分布，并且通过多数据块信息联合，也能降低个别数据块中估计出误差多途可能性，从而提升整体信道估计准确度。

图12 不同方法信道估计结果对比Fig.12 Comparison of channel estimation results of different methods

为了对比均衡后算法的性能，采用MMSE的均衡方式进行信道均衡，并且由于单个阵元SNR 较低，只有10 dB左右，因此通过多水听器联合均衡的方式来获取均衡增益。水听器合并的数量越多，合并后SNR 增益越高，因此性能的提升来源于分集作用和SNR的增加。

对每个水听器分别进行信道估计，并联合多个接收阵元所接收的信号完成信道均衡，选取其中两个信号的均衡结果进行展示，均衡后不同方法对应的误码率结果如图13所示。从图13中可以看出，两个信号的单水听器的SNR 均值分别约为10 dB 和11 dB，仅采用单个阵元进行均衡时(水听器个数为1)，3 种方法的误码率均较高，随着联合水听器数目的增加，3 种方法的误码率均明显下降，但CR-DCS方法的误码率曲线与OMP 和SOMP 相比明显降低，联合12个水听器后，误码率水平达到10−2左右。

图13 联合多水听器均衡的误码率结果对比Fig.13 Comparison of bit error rate results of joint multi-hydrophone equalization

为了验证本文所提方法对于误码率性能提升的稳定性，图14 给出了联合12 个阵元均衡后不同方法对应的误码率随信号发送轮次变化的结果，从图14 中可以看出，随着时间的变化，CR-DCS 方法具有比较稳定的误码率性能优势。

图14 联合12 个阵元均衡后不同信号发送轮次的误码率结果Fig.14 The uncoded bit error rate results of different signal transmission rounds after joint equalization of 12 array elements

对74 轮的接收信号进行总误码率统计，3 种方法对应的总误码情况见表4：74 轮信号总共发送了318200 个比特数据，3 种方法的总误码率分别为0.1433、0.0890 和0.0455，即采用CR-DCS 方法进行信道估计并联合12 个水听器的信道进行合并均衡后，其误码率相较于SOMP 方法能够稳定降低约50%，该结果表明了所提方法相较于传统的DCS 估计方法具有稳定的性能优势。

表4 联合12 阵元均衡后74 轮信号的总发送比特及误码结果Table 4 Total transmitted bits and uncoded bit error results of 74 rounds of signals after joint 12-element equalization

4 结论

针对深海OFDM 水声通信在长时延和窄带宽信道下传统CS 信道估计方法面临的所需导频密度高、频谱利用率低的问题，本文提出了一种CR-DCS信道估计方法，利用了深海远程信道的缓变特性和簇区域稳定性，采用多数据块联合的方式进行CR-DCS的OFDM信道估计，在联合字典矩阵中引入信道簇区域约束信息，通过限制信道所在簇区域来缩小有效字典原子的范围，从而降低估计差错的可能性，文中给出了具体的实现方案和算法步骤。实验结果表明了该方法相较于传统的CS和DCS信道估计算法的性能优势。采用本方法进行10 个数据块的联合信道估计，并通过12个多水听器合并均衡后，相较于传统DCS 算法，本方法能够降低50%的误码率。

致谢感谢参与本次水声通信实验的全体工作人员为本文提供了可靠的实验数据。