基于最小Csiszár’s I-散度的高精度深度定位方法∗

袁 笑 徐 铭 谢世伟 高子聪 苟欣迪

(中国海洋大学信息科学与工程学部 青岛 266100)

0 引言

在水声领域，深度的估计与判别一直是重点难点问题。基于简正波模态的深度识别与估计方法受到国内外学者的广泛关注[1−2]。郭晓乐等[3]提出了一种利用简正波模态消频散来对声源进行定位的方法。郭良浩等[4]利用水平阵模态域波束形成判别声源深度，根据声源波数谱结构和波数位置的不同来分辨近水面声源和水下声源。曹怀刚等[5]介绍了一种基于简正模态相位关系的浅海声源深度分辨方法，适用于海水声速随深度不变或缓变的水文环境。另外，于喜凤等[6]介绍了一种基于阵列不变量的浅海声源深度分类方法。近年来，模态波束形成[7−10]被广泛用于水下目标定位。模态波束形成器是一种作用在模态域的线性波束形成器，其对水平距离和深度的定位精度很大依赖于获取的模态数目。简正波理论将水听器接收到的声场分解为多号简正波的叠加，并指出短垂直阵能够对高阶简正波完整采样，但对声场贡献较大的低阶简正波采样不充分。而具有较少阵元但覆盖了整个水层的稀疏阵能完整采样低阶模态，却对高阶模态采样不足。有限的模态数直接影响了声源水平距离和深度的定位精度。一般来说，水平距离的估计精度可以在千米量级，而对深度的估计精度在百米级，前者可以接受，但对于深度的估计精度却不能满足实际需求。这就促使学者们寻找高精度深度估计的方法。另外，在混响环境中定位散射体也需要提高对深度估计的精度。例如，如果混响来自海底，想要知道混响是来自海山还是断裂区域，只有精确地知道散射体的深度才能回答这一问题。

传统的波束形成方法虽具有较好的稳健性，但得到的主瓣较宽和旁瓣较高。许多高精度算法依赖于信号协方差矩阵的准确估计，如最小方差无畸变响应(Minimum variance distortionless response,MVDR)和多信号分类(Multiple signal classification,MUSIC)算法，其具有较窄的主瓣和较低的旁瓣，但是，这些算法对信号失配很敏感—信号失配会导致部分信号被当作噪声或干扰，从而降低算法性能。为了降低对失配的敏感度，MVDR 算法加入了另外的限制条件对其进行改进，如加入白噪声增益(White noise array gain,WNG)限制[11]或分布源限制条件[12]，在获得相比原有MVDR 算法略宽主瓣的同时保持较低的旁瓣。这些算法对协方差矩阵进行对角加载，但是加载值通常是未知的，需要通过迭代搜索得到。此类高精度算法的另一个问题是信号的协方差矩阵是未知的，时常被采样协方差矩阵代替；假定接收到的信号是稳态的，那么采样协方差矩阵需要足够多的信号样本(一般是接收器数目的2∼3 倍)，以确保在波束输出时能快速收敛且能量损失最小[13]；在非稳态的环境中，例如当存在方向变化速率较大的运动声源时，用于计算协方差矩阵的样本数目变得相对较小，即所谓的快拍欠缺条件[14]。在这些(快拍欠缺)条件下，高精度算法性能较低，如果忽略非稳态条件仍然对由多个样本得到的协方差矩阵进行平均处理，波束形成器的抗干扰能力将大大降低。MUSIC 算法是一种典型的空间谱估计技术，但在低信噪比(Signal to noise ratio,SNR)和小快拍数的条件下，MUSIC 算法的分辨力下降，估计性能显著降低；另外，对于相干源的分辨，MUSIC算法失效。

基于线性系统的去模糊问题在工程应用中很常见，其本质上是一个线性求逆问题，通常被表示为第一类弗雷德霍姆积分方程的形式：

从被模糊了的输出a(y)还原出输入c(x)是一个不适定问题：a(·)和g(·)中很小的改变会导致该问题解的巨大变化。特别地，在非负条件下线性系统的求逆问题受到广泛关注。Vardi 等[15]指出非负条件下确定性的线性逆问题可以被认为是一个基于有限观察样本的统计估计问题，这就允许使用弱大数定律；因此，最大似然估计法和最大期望算法提供了一个解决此类问题的直接办法。Synder 等[16]也解决了相同的问题，他总结到基于最小Csiszár’s I-散度(Minimum Csiszár’s I-divergence,MCID)的解渐进地等效于某些特定的最大似然估计。

本文将最小Csiszár’s I-散度原理和模态波束形成相结合，提出了一种新的高精度深度估计方法。仿真结果表明，与上述经典方法相比有如下优势：

(1) 相比于传统的波束形成方法，能够实现深度的高精度定位且抑制旁瓣能量；

(2) 在低SNR 和小快拍数的情况下，对于非相干声源，深度分辨性能更加显著。另外，能够更好实现对相干声源的定位。

SWellEx-96 实验进一步验证了在小快拍数条件下，本文提出深度定位方法的有效性。

1 理论模型

1.1 模态波束形成

模态波束形成将模态滤波和波束形成处理结合，实际上是一种工作在模态域的波束形成方法。对于绝热简正波声场，距离信息只包含在信号的相位中，而深度信息包含在本征函数里，可以对垂直阵接收到的数据进行处理，分离出各阶模态幅度和相位，再应用传统波束形成(Conventional beamforming,CB)方法原理，从而在模态域估计声源的水平距离和深度。

由垂直阵接收到的声场可以表示成各号简正波的叠加形式：

其中，N代表垂直阵中的水听器个数，M代表总的简正波号数(高阶简正波被视作噪声)；φi(zj)代表深度为zj时第i号模式的幅度；这里忽略海洋中的环境噪声。模式系数ai是关于声源水平距离和深度的函数：

其中，rs和zs分别代表声源的水平距离和深度，ki代表第i号简正波的水平波数。参考公式(2),φi(zs)可被称作模式深度幅度，ai为模式距离幅度，或者简单地说是模式幅度。模式深度幅度φi(zs)和水平波数ki可以通过简正波程序计算得到，但是模式幅度ai是未知的，须从实验数据中获得。

从实验数据中得到模式幅度被称作模式分解或者模式滤波，其原理是利用各号简正波间的正交性，通过空间积分将声场投影到模式空间，从而从实验数据中得到各号简正波的模式幅度。将声场p(zj)写成N维向量的形式P，同样模式幅度ai可以写成M维向量的形式A，那么公式(2)写成矩阵的形式为

其中，E是N×M维矩阵，每个矩阵分量Eji=φi(zj)。模式幅度向量A为

得到模式幅度向量A后，应用模态波束形成(一种在波数域的求和延时算法)可以估计声源位置：

其中，B是关于水平距离r和深度z的波束输出。si代表第i阶模态的导向矢量：

公式(6)将在声源的实际水平距离和深度处取得最大值。当取得的简正波号数较大时，对于水平距离和深度的定位来说，分别有

可以认为，模态波束形成关于声源水平距离和深度的定位函数公式(8a)和公式(8b)是CB在模态域的推广。模态波束形成方法能够实现声源定位的前提是已知各阶模态的幅值大小和相位。水平距离和深度的估计精度很大程度上依赖于对向量A估计的准确度。公式(5)是一个准确的结果，但通常是奇异的，也就是说矩阵E+E通常会有一些接近0的本征值，这时可以直接用E+P对向量A近似估计，但定位结果就不够准确。如何对向量A进行准确估计不在本文的考虑范围内。

1.2 最小Csiszár’s I-散度的迭代算法

Csiszár’s I-divergence 是信息论中一种刻画两个非负函数间差异的测度，也是积分区间不相等的两个函数间Kullback-Leiber 距离的推广。Csiszár[17]总结道如果需要比较的两个函数是非负的，他提出的I-散度测度是唯一契合其提出公理的差异测度。对于非负的线性求逆问题，Synder 等[16]提出了一种最小差异测度的算法，该算法生成的序列具有许多良好的特性，如保证序列中每个估计值的非负性、单调收敛至全局最小值等，并且已经被应用在各种领域，例如，Lucy[18]和Richardson[19]将其应用到图像恢复问题中。Yang[20−21]将该序列应用到目标的方向估计问题，以实现目标方位估计的高精度和基于短阵列的超分辨率性能；在他讨论的问题中，类似于公式(1)，CB的波束能量可以表示成波束方向图案和声源(包括噪声)分布的卷积形式，其等同一个线性系统，

这里的波束方向图案Bp(sinθ|sinϑ)是当远场点源的方向正弦值为sinϑ时，该线性系统在输出方向正弦值为sinθ时的响应(即波束能量)。已知BCBF和Bp反求声源分布S(sinϑ)，这样就得到关于声源目标的方位估计。注意到Bp(sinθ|sinϑ)的移位不变性，即Bp(sinθ|sinϑ)=Bp(sinθ−sinϑ)，那么声源分布S(sinϑ)的估计问题就变成了一个典型的反褶积问题。利用上述序列[12]，反褶积作用在波束能量域(非负的)，且是适定的。在水声环境中，当海底环境参数随方位变化或接收阵列为任意形状时Bp(sinθ|sinϑ)Bp(sinθ−sinϑ)，即积分：

是关于变量sinθ的函数，不是一个定值，需要对其进行归一化处理。

类似于公式(9)，可以将公式(8b)中声源的深度分布(系统输入)和B(rs,z)(系统输出)间的关系表示为第一类弗雷德霍姆积分方程的形式：

其中，B(z)是略掉了声源水平距离rs的简略形式，x代表声源的实际深度，s(x)代表声源深度的分布，

(α为常系数)类似于公式(9)中阵列波束方向图案，代表声源深度为x时，波束能量在深度位置z的值。

公式(11)中涉及到的函数都为非负的，可以应用最小I-divergence 的迭代算法求得声源的深度分布s(x)。在实际应用中，假定变量z和x定义在有限维集，即z ⊂R，x ⊂R。那么公式(11)的离散形式可以写成：

通过最小Csiszar’s I-散度的测度：

这里B(z)是给定的波束输出，而波束输出的估计值(z)可由特定的声源深度估计分布得到：

依据库恩-塔克条件，可以得到一种使得公式(13)中I[B(z)||ˆB(z)]最小的迭代算法：

2 仿真分析

将基于SWellEx-96 实验[22]中的Event S5，用仿真和实验数据对本文提出的方法进行验证。实验布局如图1 所示，整个实验持续75 min，水深大部分在180∼220 m 间。在Event S5 中，水面科考船拖曳着两个声源—浅声源(zs=9 m)和深声源(zs=54 m)，以5 knot (约2.5 m/s)的速度由西南向东北方向匀速直线行驶。声源发出各种频率和SNR的连续波(Continuous wave,CW)信号。星号标记的垂直阵(Vector senor line array,VLA)包含21 个水听器，略有倾斜，大致均匀分布在深度为94∼212 m的水层，间隔约为5.6 m。

图1 SWellEx-96 实验Event S5Fig.1 Event S5 of the SWellEx-96 experiment

Yang[23]应用最小方差原理，得到一种高精度的深度估计方法，并比较了CB 法和最小方差(Minimum variance,MV)法定位性能。MUSIC 算法是一种基于子空间分解的算法，它利用信号子空间和噪声子空间的正交性，构建空间谱函数，通过谱峰搜索，能够实现对信号的参数的高精度估计。本文将比较MCID 法、CB 法、MV 法和MUSIC 法深度定位性能的优劣。

在1.1 节提到，深度的精确定位很大程度上依赖对模态幅度向量A的准确估计，即需准确分解各阶模态，这通常要求垂直阵的阵元数远远大于需分解的模态数。为了更好地分解各阶模态，仿真部分选取一个阵元数为100、阵元间隔为2 m 均匀分布的垂直阵列，该阵列覆盖水深为2∼200 m 的水体。基于SWellEx-96 实验的声速剖面和海底环境参数，如图2所示，用Kraken程序去仿真垂直阵接收到的声场数据。下面的仿真都假定声源静止不动，与垂直阵间的水平距离为5000 m，频率为170 Hz，共激发出21号简正波。由于选取垂直阵阵元数为100，且基本覆盖整个实验水深，能够实现对21号简正波的完整采样。由于最多选取21 号简正波，则一般需要40∼60个快拍来确保协方差矩阵收敛；本文除在讨论快拍数目对上述方法定位影响部分外，都选取50个快拍计算协方差矩阵，以保证协方差矩阵是可逆的。

2.1 高精度和低旁瓣

图3(a)为声源深度100 m、SNR为20 dB(每个阵元)，选取前20 号简正波时的深度定位图。对于这种理想情形，MCID 法的波束输出近似于深度在100 m 处的Delta 函数，几乎没有旁瓣；且主瓣宽度约为2 m，与MV 法、MUSIC 法相近。设定SNR 为10 dB，声源深度为30 m，同样选取前20 号简正波，深度定位结果如图3(b)所示。很明显，MCID 法的主瓣宽度依旧很窄；相比于图3(a)，旁瓣(类冲击曲线)能量增加，但平均输出旁瓣能量低于另外3种方法的旁瓣能量；特别地，MCID 法的峰值旁瓣比(Peak-tosidelobe-level ratio,PSR)比CB 法约高8 dB。这是因为输出噪声是波束方向图与输入噪声积分后的结果，一定程度上抑制了噪声的输出。这里设置迭代次数为1000 次，在下面的仿真讨论中，迭代次数在1000∼2000次之间；由此可得，MCID法在获得窄主瓣、低旁瓣的同时，加大了计算量。那么似乎没有必要先对接收进行模态波束形成，然后对波束形成的输出进行迭代处理，以消除由它引起的模糊效应(这里的迭代运算并不等同于去波束形成或逆波束形成，后者是为了恢复原始数据)。请注意，如果只需要估计声源的深度，则可能不需要模态波束形成。例如，人们可以使用维纳滤波的方式直接从接收到的信号中估计声源深度。首先将波束形成应用于信号的原因是利用波束形成所提供的能量增益(类似于阵列增益，模态数类似于阵列中的阵元数)来增强信号能量。然后应用该迭代算法到CB 法的波束输出能量以获得其他优势，如窄主瓣和低旁瓣。

图3 选取前20 号简正波时的深度估计Fig.3 The depth estimation when the first 20 normal modes are selected

2.2 简正波数量对主瓣宽度的影响

文献[7]表明深度的定位受限于可分解的模态数，且具体选取多少号模态就能达到对深度的定位还与相应的波导环境、阵列孔径等相关。就本文考虑的仿真条件而言，若要达到精度小于40 m 的深度定位则至少需5 号简正波；另外，一般来说，选取的简正波数量越少，相应波束输出主瓣宽度也越宽。本节讨论了前不同简正波号数对4种方法深度定位精度性能的影响。假定声源深度为100 m，SNR 为20 dB，选取前5 到20 号简正波，图4 为4 种方法主瓣宽度(波束能量为−3 dB 处)随简正波号数变化的折线图。由图4 可得，随着简正波号数的减少，4种方法的主瓣宽度也逐渐增加；在选取前不同号的简正波的条件下，相比于CB 法，MCID 法的主瓣宽度窄且变化不大，变化范围在2∼4 m 内，与MV 法、MUSIC法等高精度算法相近，验证了MCID方法深度定位的高精度性能。

图4 主瓣宽度随简正波号数的变化Fig.4 The mainlobe width varies with the number of normal mode

2.3 两个相干声源的定位

对于两个相干声源的定位而言，MV 法和传统的MUSIC 法的定位性能将显著下降。为比较4 种方法对两个相干声源的定位性能，进行如下仿真实验，选取前20 号简正波，每个阵元的接收信号为两个等能量相干声源(深度为30 m 和100 m)发出信号的叠加，SNR 为20 dB。定位结果如图5 所示，MCID 法和CB 法能够准确辨别出两个不同深度的相干声源，但相比于CB 法，MCID法定位精度更高，旁瓣更低；由于声源间的相干性，MV 法和MUSIC法定位效果很不理想，PSR 仅为3 dB，而MCID 法和CB法的PSR远大于3 dB。注意到接受到的信号为两个不同深度(30 m 和100 m)声源发出的相干信号的叠加，这会导致其他深度处的波束能量输出增加，进而引起旁瓣能量的整体增加。

图5 水平距离相同、深度不同的两个相干声源深度定位Fig.5 Depth localization of two coherent sources at same range but different depths

2.4 SNR和快拍数对声源分辨性能的影响

在实际应用场景中，如在快拍数少、SNR 低情况下，协方差矩阵的估计存在较大偏差，这会导致特征分解协方差矩阵得到的噪声和声源信号特征值之间的差异减弱，从而使得MUSIC 算法的性能显著下降。对于两个相邻深度的非相干声源，MUSIC算法的分辨性能将明显下降。MV 方法需大量的快拍来保证协方差矩阵的可逆性，同时SNR也会影响其对相邻声源的分辨能力。下面将比较上述4 种方法在低SNR 和小快拍数条件下对相邻非相干声源的分辨性能。

假定深度分别为100 m 和108 m 的两个等能量的非相干声源，水平距离均为5000 m，SNR 为−5 dB，取前20 号简正波。深度定位结果如图6 所示。可以发现此时CB 法、MV 法和MUSIC 法已几乎不能分辨出两个声源，3 种方法在该场景下均失效；而MCID 法在100 m 和108 m 附近仍有两个尖锐峰值，较为准确地实现了相邻深度非相干声源的分辨。

图6 水平距离相同、深度不同的两个非相干声源深度定位Fig.6 Depth localization of two incoherent sources at same range but different depths

除SNR 外，保持上述实验条件不变；图7(a)为相同快拍数(50)下，MCID 法、MV 法和MUSIC 法分辨力随SNR 变化的分辨概率折线图。该试验中，SNR 间隔为1 dB，从−10∼0 dB 均匀变化。对3 种算法进行500 次蒙特卡洛仿真实验。图7(a)结果表明，随着SNR 增加，3 种算法成功分辨率也逐渐增加，但MCID 法成功分辨率明显高于MV 法和MUSIC法。图7(b)为相同SNR下，3 种算法随快拍数变化的成功分辨概率折线图。SNR 为−5 dB，快拍数间隔为10，从10∼150 均匀变化，同样取前20号简正波且对3 种算法进行500 次蒙特卡洛仿真实验。选取的简正波号数为20，当快拍数较小时计算的协方差矩阵不可逆，从而导致波束能量图中出现高旁瓣和畸变主瓣，故这里不考虑MV 法在快拍数为10、20 和30 时的分辨性能。由图7(b)可得，随着快拍数的增加，3 种算法的分辨能力也逐渐提升；同样相比于MV法和MUSIC法，本文提出的MCID法分辨性能更加优越。注意到由于相邻声源接近，CB 法在上述场景下已完全失效，故不讨论此时CB法的分辨能力。综上所述，相比于传统的CB法、MV法和MUSIC 法，本文提出方法能获得更好的相近非相干声源的分辨性能。

图7 不同SNR 和快拍数下的成功分辨率Fig.7 Successful resolution at different SNR and snapshot

MUSIC 方法还需已知声源数目D(声源+干扰)以区分声源信号和噪声的特征向量，当SNR 较低且存在强干扰时，对应于声源和噪声的特征值将难以区分，从而导致对声源的错误定位。假定存在一个强干扰和一个声源目标，两者非相干，干噪比为−5 dB，信干比为−7 dB，深度分别为50 m 和150 m，水平距离均为5000 m，取前20 号简正波，深度定位结果如图8 所示。由于SNR 较低，对应于声源信号和噪声的特征值相差不大且都小于强干扰的特征值，在当前仿真条件下，对基于模式幅度向量A(归一化后)得到的协方差矩阵进行特征值分解，得到从大到小排列后的前5 号特征值依次为0.4918、0.0953、0.0777、0.0544、0.0410；可以发现，此时声源信号对应的特征值0.0953 和后面噪声的特征值难以区分，在实际处理中，若不已知声源数目D，易将声源信号等同于噪声。结合图8(a)和图8(b)可得，若未知声源数目D，错取D=1，MUSIC方法只能辨别出深度在50 m 处的强干扰；而MCID 法、CB 法和MV 法仍在深度为150 m 的声源位置处出现峰值。在图8(a) 中，由于声源信号和噪声能量相差不大且存在强干扰，导致一部分声源信号能量泄漏到干扰和噪声空间，进而引起MUSIC 法在声源位置处输出能量的降低。

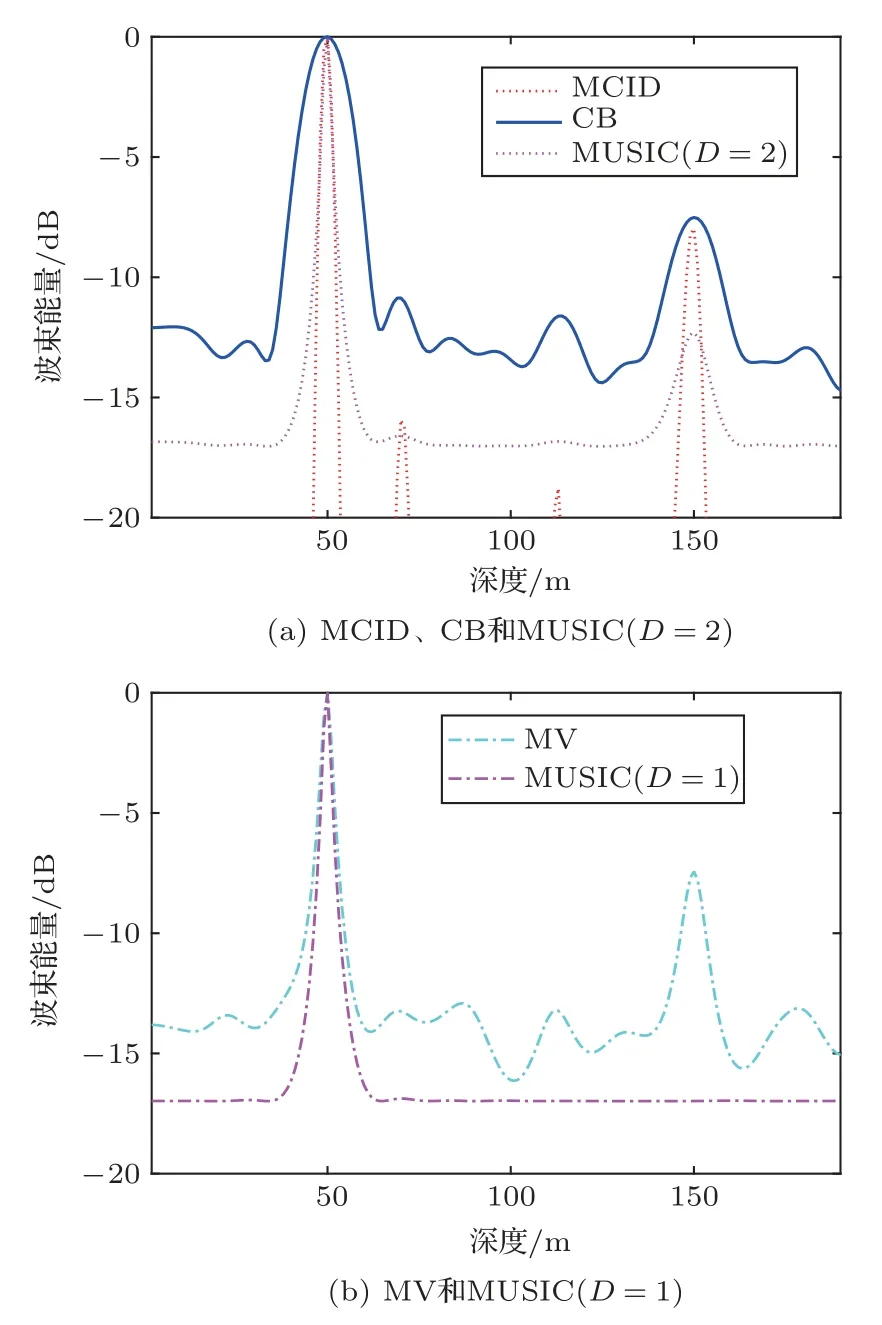
图8 强干扰+目标声源深度定位Fig.8 Depth localization for strong interference+target source

2.5 简正波数量和SNR对迭代次数的影响

对MCID 法而言，选取不同的简正波号数和SNR所需的迭代次数不同，本节将讨论选取前不同号简正波和SNR 对MCID 法迭代次数的影响。假定SNR为20 dB，声源深度为100 m，图9(a)为选取前L号简正波，主瓣宽度随迭代次数(迭代次数范围为10∼3000 次)变化图。由于深度搜索的间隔为1 m，随着迭代次数的增加，主瓣宽度阶梯式地下降；主瓣宽度收敛至2 m 时，前20 号、16 号、14 号、12号、8 号简正波所对应的迭代次数分别为871、963、1212、1561 和1624，可以得到随着简正波数目的减少，主瓣宽度收敛至2 m 处的迭代次数增加。声源深度为100 m，选取前20 号简正波，图9(b)为不同SNR(单位为dB)条件下，主瓣宽度随迭代次数(迭代次数范围为20∼3000 次)变化图。同样可以发现随着SNR的降低，主瓣宽度收敛至2 m 处的迭代次数也逐渐增加。本文选取的迭代次数在1000∼2000次之间，在选取简正波数目较少或SNR 较低时，主瓣宽度虽有变化但较小(变化范围在2 m 内)，对上面的仿真讨论影响不大。

图9 不同简正波号数和SNR 下的迭代次数Fig.9 The iterations under different normal modes and SNRs

3 实验数据分析

利用SWellEx-96 实验的Event S5 中垂直阵数据进行处理。这里分别选取1500 s(水平距离约为5200 m)和2000 s(水平距离约为4000 m)附近时间长度为20 s 的垂直阵数据进行深度定位。选取频率分别为130 Hz 和127 Hz 的实验数据，SNR 在15∼20 dB 之间，此时共激发出17 号简正波，其中前者选取前12 号简正波，后者选取前17 号简正波；声源深度分别约为54 m 和9 m，利用MCID法、CB法、MV 法和MUSIC 法对深度进行估计，其结果如图10 所示。由于声源的运动，可用于估计协方差矩阵的快拍数大大减少；这里选取10 个快拍(∼2 s)估计协方差矩阵，由于估计的协方差矩阵是不可逆的，对于MV 方法，采用对角加载的方法进行定位，一般来说对角加载值是不确定的，只知道其上下界限，这里对角加载值选为0.08；由于对角加载相当于人为地加入噪声，这会降低MV 法的定位性能。垂直阵的阵元数为21，而共激发出17 号简正波，在计算过程中矩阵E+E并不可逆，本文用向量E+P近似估计向量A，其对接收到的垂直阵数据的模态分解效果并不理想；另外，声源的运动会引起快拍欠缺；这都会导致最后估计的协方差矩阵存在较大偏差。由图10可得，相比于CB 法、MV 法和MUSIC法，MCID法具有更窄的主瓣宽度和更低的旁瓣，与上述仿真结果类似；且由于未能对协方差矩阵进行准确估计，MV法和MUSIC法的定位性能显著下降，主瓣宽度变宽，PSR 在3∼4 dB 之间，远小于MCID法和CB法。

由于科考船在运动过程中会随着海面上下起伏，拖曳声源也会随之抖动，再加上垂直阵的倾斜、海洋环境参数的变化等原因，在实际处理中，深度定位往往会出现偏差：如在图10 中，可以看到基于MCID 法声源深度的估计与实际声源深度有一定偏差，如在图10(a)和图10(b)中，深度估计约为58 m(偏差为4 m)；图10(c)和图10(d)中，深度估计为12 m (偏差为3 m)。其偏差受CB 法影响，因为MCID 法本身就是基于CB 法的波束能量输出实现深度估计的，虽有偏差，定位结果仍然可以接受；这在一定程度上也验证了MCID法的稳健性。

4 结论

基于传统模态波束形成的深度定位方法精度不高，为了提高深度定位的精度，可以将许多目标方位估计高精度算法的原理应用到深度定位。但高精度算法也存在着各种各样的问题，如自适应的高精度方法(如MVDR)会由于方向变化速率过大的声源目标而面临快拍欠缺问题。本文基于最小Csiszár’s I-散度的迭代算法，提出一种新的高精度深度定位方法。由仿真和实验数据可以得到，该方法能够实现深度的高精度定位。由于该方法是对接收到的数据进行模态波束形成处理后，再估计出原来的声源深度的分布状况，实际上解决的是线性系统的求逆问题，这相当于一个去模糊处理，一定程度上能减少噪声对实际声源分布的影响，从而能够在保持深度定位高精度的同时抑制旁瓣。当然该方法也存在不足，如本文的实验条件下，迭代次数达到数千次，这大大增加了计算量。下一步的工作是探索减小计算量的方法并将最小Csiszár’s I-散度的迭代算法应用到对水平距离和深度的同时估计。