有限元/边界元耦合方法在海洋生物目标强度特性研究的应用∗

于小涛 王新良 张吉昌 赵宪勇

(1 中国水产科学研究院黄海水产研究所 农业农村部极地渔业可持续利用重点实验室 青岛 266071)

(2 深蓝渔业工程联合实验室 青岛 266237)

(3 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)

0 引言

目标强度(Target strength,TS)特性是海洋生物声学识别和资源量评估的重要依据[1−4]，基于理论模型法的数值仿真是TS 特性研究的重要手段。受计算方法与能力的限制，最早将海洋生物目标近似为规则的球体、圆柱体以及椭球体等具有解析解的模型[5−6]，特别是具有纺锤体形状的鱼类，一般利用回转椭球体模型(Prolate spheroid model,PSM)求解散射声场。为简化解析求解的难度，Stanton[7]进一步将回转椭球体、弯曲圆柱体等截面为圆形的目标分割为一系列的有限长圆柱体，提出了基于模态级数的形变圆柱体模型(Modal series-based deformed cylinder model,MB-DCM)，该模型适用于高长短轴比、声波近垂直入射的情况，被Gorska[8]应用于鲱鱼的声散射特性研究。Foote 等[9]针对鳕科(Gadidae)鱼类等尺寸较大的不规则目标，基于高频近似发展了Kirchhoff近似模型(Kirchhoffapproximation,KA)。Clay 等[10−11]提出了一种考虑鱼体和鱼鳔相互作用的Kirchhoff射线模型(Kirchhoffray mode,KRM)，在低频区域结合MB-DCM研究了大西洋鳕鱼(Gadus morhua)的TS 特性。对于磷虾类(Euphausia)和桡足类(Copepoda)等自身声阻抗与其所处媒介相近的弱散射目标，Chu等[12]和Stanton 等[13]建立了畸变波波恩近似模型(Distorted wave born approximation,DWBA)。我国学者在渔业种类TS 研究方面以实验测量为主[14−17]，数值仿真研究主要将MB-DCM、PSM、KRM和KA等近似模型应用于我国的海水及淡水鱼类[18−22]。这些模型对声波频率、入射角度以及目标声阻抗、形态尺寸等各自均有不同条件的限制[23]，以致于有时同一模型难以描述不同种类或同一种类但不同尺寸的生物种类，使得这些模型各自存在其适用的局限性。

有限元方法(Finite element method,FEM)[24−25]是近些年兴起的数值求解方法，相比于当前普遍使用的KRM 和MB-DCM 方法要求满足声波近垂直入射、目标高长短轴比及声阻抗均匀等条件，以及DWBA 模型仅适用于与其所处媒介声阻抗接近的弱散射目标，FEM 能够适用于全频段、任意形状、任意非均匀声阻抗目标的声散射求解，且数值计算精度高。Forland 等[26]利用FEM 研究了玉筋鱼(Ammodytes personatus)的宽频声散射特性，并分析了骨骼对反向散射强度的贡献。由于TS 关注的是远场问题，单纯利用FEM 需要较大的求解域，产生额外的计算量。针对远场辐射与散射问题，声学领域新兴的有限元/边界元(Finite element method/boundary element method,FEM/BEM)耦合分析方法[27−33]分别利用FEM和BEM 求解目标边界和外部声场，既能保证模型准确性，又有效降低了单纯FEM 的计算时耗。目前，FEM/BEM 耦合方法正逐步应用于舰船、潜艇等大目标的低频声辐射与声散射特性研究，尚未推广到鱼类等海洋生物目标。

本文以球形生物、尾明角灯鱼(Ceratoscopelus warmingii)和南极大磷虾(Euphausia superba)等为例，利用FEM/BEM耦合方法仿真计算其TS，通过与球形目标的解析模型、MB-DCM 和DWBA 等传统理论模型的数值计算结果对比，分析FEM/BEM耦合模型的可靠性及优势。

1 声散射求解方法

1.1 FEM/BEM耦合方法

FEM 用于在频域数值求解非均匀Helmholtz方程得到声压的稳态解。散射体被均匀介质和完美匹配层包围，需对整个域进行网格剖分，远场散射声压由目标边界声场的Helmholtz-Kirchhoff积分求得。BEM 通过目标表面的声压和法向声速求解边界上的Helmholtz-Kirchhoff积分方程，仅需对目标表面进行网格剖分，一般用于辐射问题；而对于多数的散射情况，目标表面声压和法向声速是未知的。FEM/BEM耦合方法将BEM看作一种对FEM的补充，对目标体的内部问题使用FEM，对辐射区域的目标体外部问题使用BEM，前者得到目标表面声压和法向速度，后者得到远场辐射声压。该方法可以求解具有任意形状、任意材料的非均匀目标的散射声场。

理论方程 散射目标的内部声场利用FEM 求解，声压满足Helmholtz方程[34]：

其中，k1=ω/c1，p1为目标内部声压，ω为入射声波角频率，c1为目标体内声速。目标外部声场通过BEM 求解，声压可由Helmholtz-Kirchhoff积分计算[34]：

其中，k=ω/c，c为目标所处媒介的声速，p2=ps+pinc，ps为散射声压，pinc为入射声压。G(r,r0)为外部自由场的格林函数，r为散射声场场点的位置，r0为散射目标表面单元的位置，与目标的倾角θ有关。边界上满足p1s=p2s的声压连续条件。TS可由反向散射声压求得：

声散射仿真过程 散射声场的数值仿真采用COMSOL Multiphysics®5.4 软件[35]，主要步骤如下：

TS基于稳态声场计算，鱼鳔和鱼体简化为流体介质(只有纵波)[8]，采用压力声学(频域)和压力声学(边界元)的物理场接口进行FEM/BEM 耦合求解。前者计算目标内部及表面声场，求解域为目标实体；后者根据表面声场计算外部辐射声场，求解域为外部无限域。在边界元物理场中添加入射声压，包括入射声压的频率与方向。

目标几何形态方面，COMSOL 既支持简单的几何实体建模，也支持其他建模工具的几何导入。一般通过X 射线或CT 成像得到其三维形态结构，通过直接绘制或外部导入以重构目标。

定义目标及周围水体的密度与声速、目标的倾角等变量。

目标网格剖分采用自由四面体网格自动剖分方法基本满足计算需求，网格单元尺寸不超过波长的1/6。此外，需通过对计算结果进行收敛性测试，优化网格划分。

频域求解中频率是必要的参数，如果求解频率响应，需添加参数化扫描。海洋生物在水下的体长、倾角均具有不确定性，一般需要对其TS 进行统计平均，通过添加参数化扫描，可以求解不同体长、倾角时的散射声场。

1.2 球形目标的解析模型

解析模型主要基于分离变量法求解散射声场，球体目标反向散射函数的表达式为[5,23]

其中，An=−1/(1+iCn)。渔业相关生物种类的组织器官主要呈流体态(气态和液态)，根据声压和声速连续的边界条件求解得到[5,23]：

其中，jn和yn分别为第一类和第二类n阶球贝塞尔函数，分别是jn和yn的一阶偏导数，g和h分别为目标与其所处媒介的密度比和声速比，k是声波在海水中的波数，k1是声波在目标体内的波数，a为球体半径。目标的反向散射截面为

TS由反向散射截面求得：

1.3 MB-DCM模型

MB-DCM 模型主要用于求解圆形截面、高长宽比目标在近法向入射时的散射声场。以有鳔鱼类为例，将鱼体和鱼鳔分别简化为充满气体和液体的回转椭球体，其反向散射函数可表示为[8]

其中，l是目标(鱼体或鱼鳔)的长轴长度，u=x/(l/2)，x是沿长轴的圆柱散射体微元相对于长轴中心的距离，D(θ)是反向散射的倾角指向性函数，函数bn的表达式为[8]

其中，εn是诺伊曼系数，当n=0时，εn=1；当n>0时，εn=2。Jn和Nn分别是第一类和第二类n阶柱贝塞尔函数，分别是Jn和Nn的一阶偏导数，是圆柱微元的横截面半径，w为短轴长度。鱼鳔和鱼体的反向散射指向性函数表达式分别为[8]

其中，下标sb和b分别代表鱼鳔和鱼体，θ是入射声波相对于目标长轴的夹角，∆θ是鱼鳔相对于鱼体的夹角。因样品均系出水后采集，即相当于样品取自表层，因此文中数值计算中均将z设置为0 m。

1.4 DWBA模型

DWBA 模型主要用于目标与其所处媒介声阻抗相近的声散射(如浮游动物)求解，对于截面为圆形的细长形目标，可简化为沿其中心轴线的一系列充满流体介质的离散圆柱体微元，Stanton 等[13]求得DWBA模型的一维线性解，反向散射函数表达为

式(14)中，k1i为入射波在目标体内的矢量波数，r0表示圆柱体微元中心的矢量位置，βtilt表示圆柱体微元截面与入射波之间的夹角，aj表示每个圆柱体微元的半径，J1表示第一类1 阶柱贝塞尔函数。压缩系数γk和γρ分别为

其中，ρ和c分别表示目标所处媒介的密度和声速，ρ1和c1表示目标体内的密度和声速。对于圆弧形弯圆柱体近似目标，公式(14)可简化为[13]

其中，ρc表示弯圆柱的曲率半径。

2 TS仿真结果

海洋生物目标与其所处媒介(周围水体)的密度比和声速比采用前人的测量结果[5,36]，如表1所示。

表1 目标与其所处媒介(周围水体)的密度和声速比[5,36]Table 1 Density and sound speed ratio between the target and surrounding water[5,36]

2.1 球形生物

桡足类浮游动物一般可以被近似为液态球形目标，而受数值计算方法与能力的限制，早期将浮游动物和鱼类也近似为球形目标。由于球形目标的散射声场具有精确的解析解，本文将其用于验证数值模拟方法。以充气(气泡)和液态球体为例，分别利用球形目标的解析模型和FEM/BEM 模型计算其TS。球体半径假设为10 mm，充气球体和液态球体的密度比和声速比见表1。TS随频率变化的计算结果如图1所示。图1显示，FEM/BEM模型计算结果与解析解高度吻合，充气球体的TS 远大于液态球体。

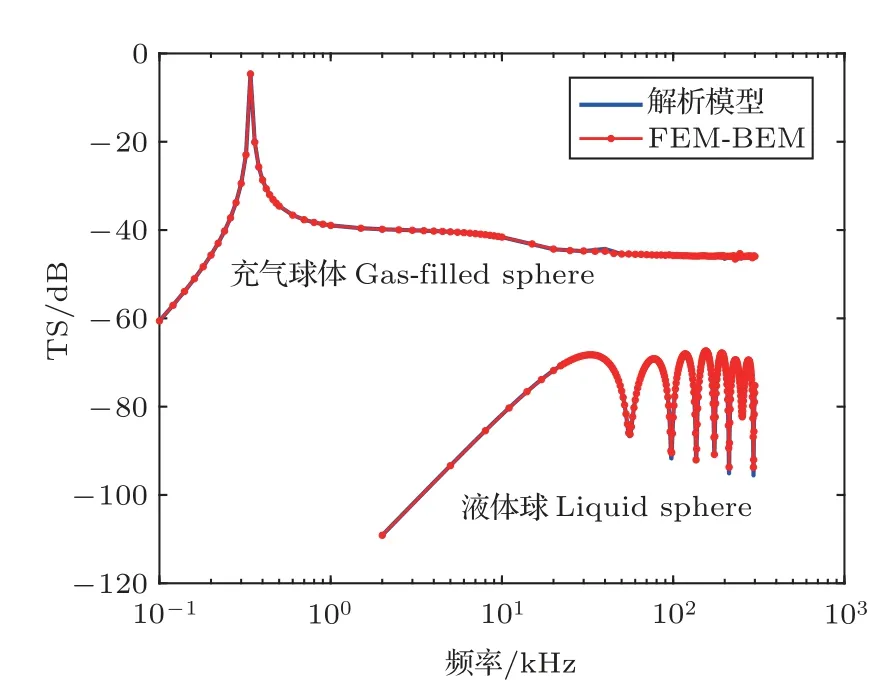
图1 充气和液态球体TS 的频率响应Fig.1 Frequency response of TS for a gas-filled and liquid sphere

2.2 纺锤形鱼类

对于纺锤形鱼类，可将其形态近似为回转椭球体，以南海尾明角灯鱼(图2(a))为例，通过X 射线扫描(图2(b))并测量得到鱼鳔和鱼体的形态学参数见表2，近似的回转椭球体如图2(c)所示。有鳔鱼类的声散射主要来自鱼鳔，因此以鱼鳔TS 代表尾明角灯鱼；以鱼体TS 代表同类体型的无鳔鱼类。鱼鳔和鱼体的物理参数分别采用表1 中充气和液态椭球体的参数。鱼鳔的TS 计算采用MBDCM、FEM/BEM 以及Ye[37]的低频修正模型，鱼体TS 的数值计算采用MB-DCM、FEM/BEM 以及DWBA 模型，数值求解得到鱼鳔和鱼体TS 随频率和倾角的变化分别如图3∼5所示。

图2 尾明角灯鱼的形态学建模Fig.2 Morphological modeling for a Ceratoscopelus warmingii

图3 尾明角灯鱼鱼鳔和鱼体TS 的频率响应Fig.3 Frequency response of TS for a Ceratoscopelus warmingii with a swimbladder

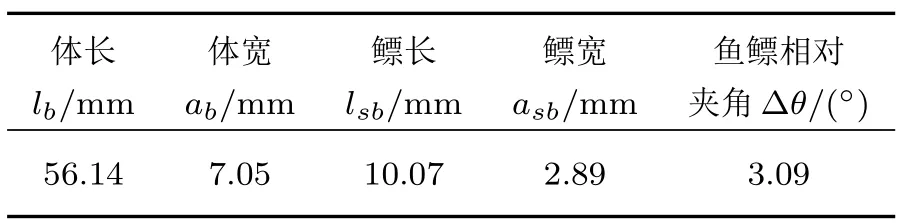
表2 7 条尾明角灯鱼样品的平均形态参数Table 2 Mean morphological parameters of 7 Ceratoscopelus warmingii samples

图3 为垂直鱼体长轴方向(倾角为0◦)入射时，鱼体和鱼鳔TS随频率的变化。对于鱼体，MB-DCM和FEM/BEM 模型得到的结果除共振频率附近基本一致；对于鱼鳔，FEM/BEM模型和MB-DCM 模型在共振附近的结果差别非常大，这是由于鱼鳔长短轴比值约3.5 : 1，不足以满足其高长短轴比的适用条件。Ye[37]建立的充气椭球体低频声散射模型对MB-DCM 模型共振频率附近的结果进行了修正，并通过解析模型进行了验证；同时，他发现MB-DCM 模型的准确性随着回转椭球体长轴与短轴比值的升高而提高。本文中，FEM/BEM 模型在共振频率附近的结果与Ye的结果基本吻合，高频计算结果与MB-DCM模型计算结果相近。

图4为38 kHz和120 kHz频率入射下，鱼鳔TS随鱼类游泳倾角的变化。结果显示，FEM/BEM和MB-DCM 模型的计算结果差别非常大，FEM/BEM 模型计算的TS 从垂直入射(倾角为0◦)向两端入射随倾角的增加TS 减小的速度更慢，且曲线相对平滑，没有峰值和谷值的震荡起伏。图5 为38 kHz和120 kHz入射频率下，鱼体TS随倾角的变化。由图5可知，在垂直入射方向附近，FEM/BEM、DWBA 和MB-DCM 模型的计算结果一致，但随着倾角的变化，3 种模型计算结果的差异逐渐增加；FEM/BEM 和MB-DCM 模型吻合的倾角范围极窄，FEM/BEM 模型和DWBA 模型吻合的倾角范围较宽。

图4 鱼鳔TS 的倾角分布Fig.4 TS as a function of tilt angle for the swimbladder

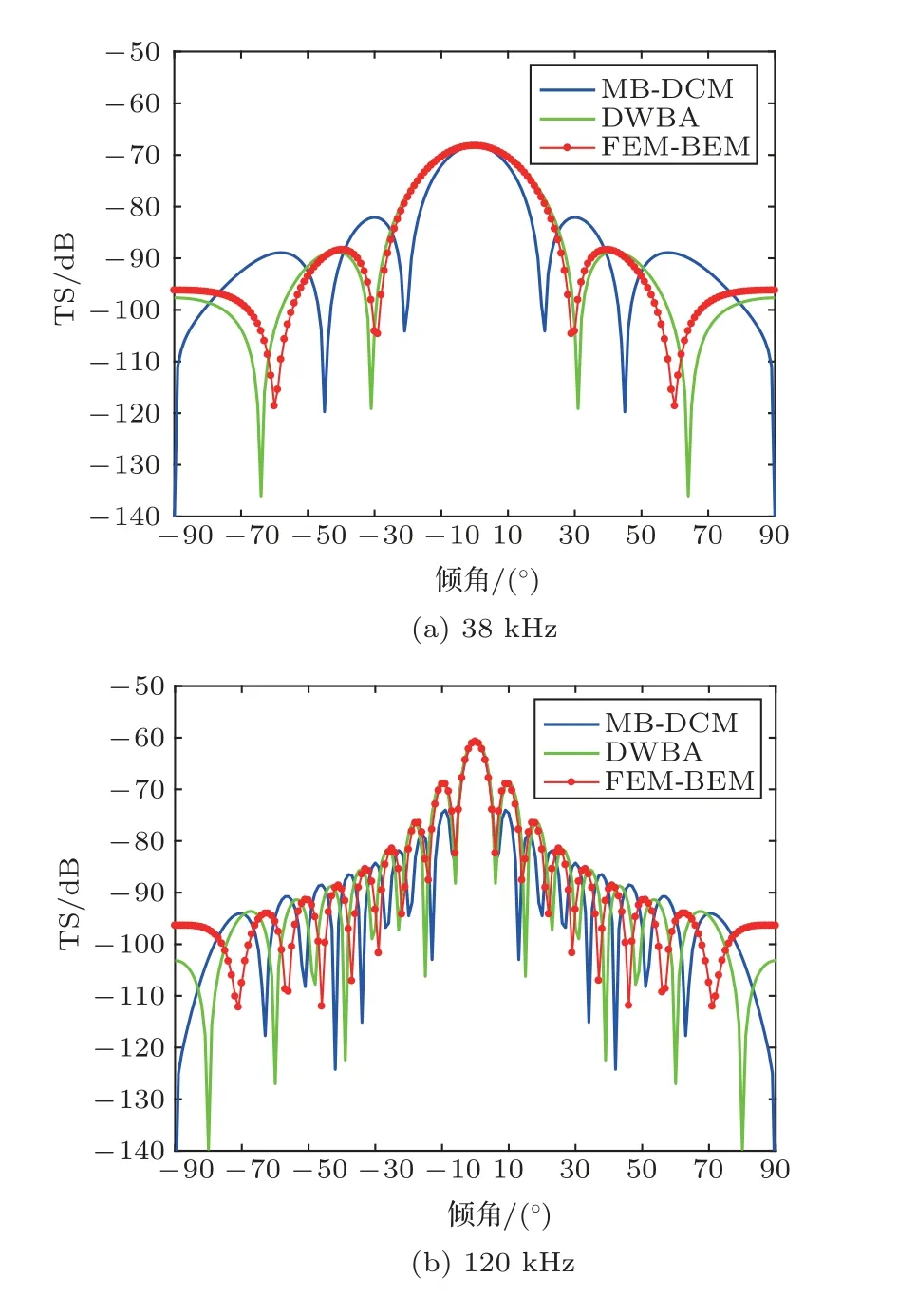
图5 鱼体TS 的倾角分布Fig.5 TS as a function of tilt angle for the fish body

2.3 细长形浮游动物

对于细长形浮游动物，以南极大磷虾(图6(a))为例，可将其近似为呈圆弧形弯曲的形变圆柱体，如图6(b)所示。假设圆柱体长度L=38.35 mm[36]，截面半径为a=L/10.5，曲率半径ρc=10L，声学参数采用表1 中弯曲圆柱体的参数。采用FEM/BEM和DWBA 模型数值求解得到TS 随频率和倾角的变化分别如图7 和图8 所示。图7 表明，FEM/BEM模型得到的垂直入射时TS频率响应曲线与DWBA模型计算结果比较一致，在曲线峰值和谷值处两者的结果有所差异。图8 表明，FEM/BEM 模型得到的TS 随倾角的变化曲线与DWBA 模型计算结果整体比较吻合，但随着倾角增加，两者计算结果的差异逐渐增加，尤其曲线峰值和谷值处。

图6 南极大磷虾的形态学建模Fig.6 Morphological modeling of Euphausia superba

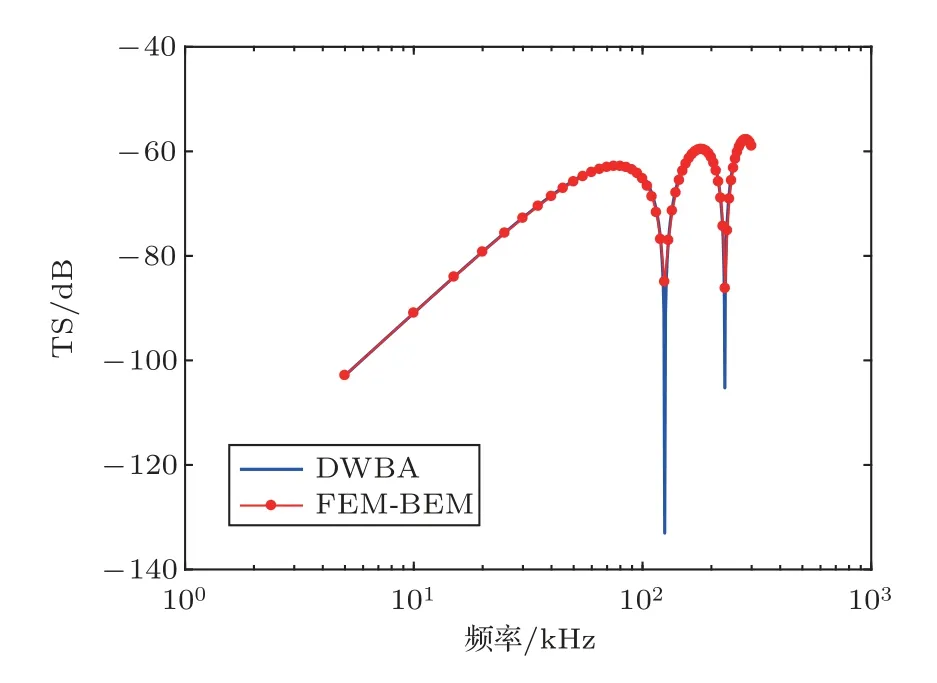
图7 南极大磷虾TS 的频率响应Fig.7 Frequency response of TS for an Euphausia superba

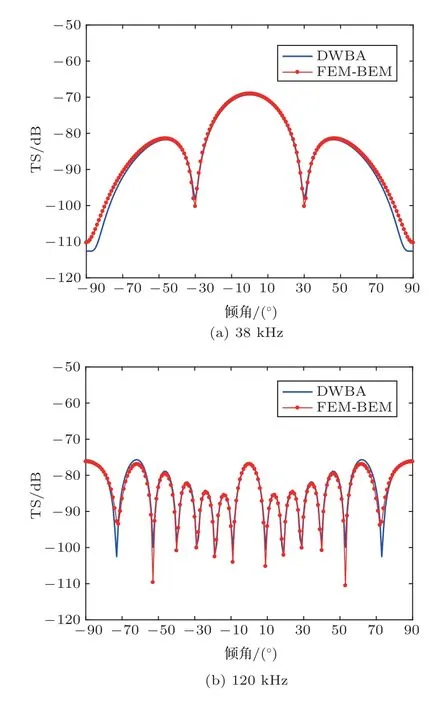
图8 南极大磷虾TS 的倾角分布Fig.8 TS as a function of angle of incidence for an Euphausia superba

3 结论与讨论

文中利用国际上已广泛应用的MB-DCM 和DWBA 散射模型验证FEM/BEM 耦合方法在海洋生物声散射研究的适用性，尾明角灯鱼的形态学参数为本研究团队前期基于X 射线扫描的实测结果[38]，南极大磷虾的形态学参数和声学参数采用南极海洋生物资源养护委员会(CCAMLR)推荐的标准[36]。基于FEM/BEM 耦合方法的球形生物声散射模型与解析模型TS 的计算结果完全吻合，验证了FEM/BEM 耦合模型的可靠性。对于纺锤形鱼类的鱼鳔，FEM/BEM 模型既解决了MB-DCM模型在中低频段的准确性问题，又弥补了Ye 低频散射模型在高频段时的不足；对于鱼体(无鳔鱼类)，FEM/BEM 与DWBA 模型的仿真结果相近；在倾角变化时，FEM/BEM 和MB-DCM、DWBA 模型得到的TS 峰值和谷值出现在不同角度，且倾角越大，两者偏差越大(如图4 和图5 所示)。对于细长形浮游动物，FEM/BEM 与DWBA 模型的仿真结果高度一致。但DWBA 模型的基础是玻恩近似理论，仅仅适用于密度和声速与其所处媒介(周围水体)接近的弱散射目标(如浮游动物)，即目标与周围水体的密度、声速比接近1[23]，不适用于有鳔鱼类等含气囊海洋生物的TS 计算；而FEM/BEM 耦合方法可仿真具有不规则形态和不均匀参数的任意目标(有鳔鱼类、无鳔鱼类、浮游动物等)，能够更精确地模拟生物各部分的声散射，且适用于所有入射频率和入射方向。因此，FEM/BEM 耦合方法在具有不同复杂形态的海洋生物TS 仿真研究方面的应用前景广阔。

关于FEM/BEM 与MB-DCM 模型仿真结果随倾角增加产生的差异，主要由于MB-DCM 模型的TS 表达式是在声波近似垂直入射、目标高长短轴比的假设下推导得到的[7]，当倾角增大时模型自身的适用性降低；FEM/BEM 和DWBA 模型理论上均适用于全入射角度，但两者随倾角增加也产生一定差异。因此，FEM/BEM 模型在声波端向入射时的准确性尚需进一步验证。由于FEM/BEM耦合方法具有可仿真非均匀目标散射的优点，后续应用于海洋生物声散射建模时将对目标的形态学参数和声学参数作精细测量，充分发挥其可构建更精准物理模型的优点。对于无其他理论模型可仿真对比的非均匀目标的散射，需结合实验测量进一步验证FEM/BEM耦合方法的可靠性。

海洋生物普遍以大量尺寸不一、游泳倾角不同个体构成的集群形式混合栖息于海洋环境中，因此，对不同生物集群的分类识别、资源量评估有实际应用价值的是鱼群的散射特性(如频率响应特征、平均单体TS)。后续在单体TS 特性研究的基础上，将考虑生物集群中大量单体的体长、游泳倾角的统计特征，分析生物集群的平均散射频率响应特征和平均单体TS，推动FEM/BEM 耦合方法实际应用于海洋生物资源声学资源评估。

由于FEM/BEM 耦合方法基于对目标几何的网格化离散求解波动方程，计算结果的准确性很大程度上取决于网格的疏密，一般网格最大尺寸不超过声波波长的1/6。因此，频率越高(目标尺寸与入射声波波长的比值越大)，网格剖分越密，FEM/BEM 耦合方法对计算能力的需求呈指数增长。考虑到未来研究生物集群的散射特性需在体长、游泳倾角的二维空间进行统计平均，FEM/BEM耦合方法计算过程中对频率、体长、游泳倾角3 个维度进行参数化扫描，计算量较大。因参数化扫描产生的计算量，常用的解决方案是增加计算节点、利用并行计算等方式。同时，可结合几何模型的优化，充分利用目标的对称性以降低计算规模；对于具有不规则几何形状的生物，可将其细分为更小的子域，合理设置网格大小，通过收敛性试验，保证一定计算精度的前提下，提高单次计算效率。