水平线列阵方位-相速度联合的卡尔曼滤波方法∗

李 鑫 郭良浩 章伟裕 徐 鹏 陈连荣 段正辰

(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)

(2 中国科学院大学 北京 100049)

(3 中国人民解放军92330 部队 青岛 266102)

0 引言

目标运动分析(Target motion analysis,TMA)一直以来都是水声领域研究的热点问题，其中纯方位目标运动分析[1−9](Bearings only target motion analysis,BOTMA)方法只需利用目标的方位信息就可以实现对目标位置、运动参数的估计，因而实现相对简单，在工程上得到了广泛应用。由于观测站测量的目标方位是BOTMA 方法唯一可利用的信息，因此观测站测量的目标方位精度将影响BOTMA 的性能，通常随着测量方位误差的增加，BOTMA性能快速下降。

为了解决目标方位估计误差造成的BOTMA性能下降的问题，提高基阵被动测向精度是一个重要的研究方向。已有相关的科研人员研究了影响基阵被动测向精度的因素，并取得了一定的研究成果。宫在晓等[10]指出参考声速的选取是否准确对传统的水平线列阵被动测向结果有很大的影响，此影响与信号的入射方向有关：对目标信号近基阵端射方向入射时产生的影响大于信号近基阵正横方向入射时的影响，并基于简正波理论指出由于浅海中声波是以多模态形式传播，参考声速与接收阵处的相速度密切相关，其中相速度大小是由声源频率、声源距离、收发深度和传播信道等因素决定。由于被动测向时声源距离未知，因此在对目标角度估计时选取的参考声速与接收阵处的相速度往往存在偏差，从而影响基阵测向精度[11]。

近年来，已有学者对减小因参考声速选取偏差导致的测向误差，从而提高基阵测向精度的方法开展了大量研究。宫在晓等[10]将匹配场方法应用于声场测向，通过多次计算拷贝场，将与观测场最相关的拷贝场的声源角度作为估计角度，无需进行波束形成等信号处理方法进行角度估计，所以不需要考虑参考声速，避免了因参考声速选取不准确造成的目标测向误差，但该方法要求对所在海洋环境参数准确已知，且通常需要对距离、角度进行极大值的搜索，导致了计算量的大量增加。文献[12–14]提出了声速无关水下波达方向估计方法，通过使用两条线阵，对每条线阵的接收信号分别进行处理，利用两条线阵之间的几何关系，得到与声速无关的估计结果。该方法虽然能消除声速对于估计结果的影响，但需要复杂度很高的匹配算法，分别对两条线阵的数据进行处理，计算量大，估计速度慢。吴俊楠[11]提出了令水平线阵绕轴向机动，根据机动前后阵列测向结果相对于参考声速的变化曲线，修正由于参考声速选取偏差导致的测向误差的方法。当目标静止或运动较慢时参考声速短时间内变化不大，此方法校准获得的参考声速可以提高此范围内测向的精度。但是对于目标运动较快时，参考声速变化较大，此时校准参考声速需要阵列多次机动，代价较高。

为了校准参考声速，提高目标角度估计精度，本文提出了将声传播相速度作为估计状态量，改善了由于参考声速选取偏差导致的测向误差的问题，同时提高了BOTMA 的跟踪性能。文章首先分析了参考声速对传统水平线列阵被动测向精度的影响，给出了在确知环境下的两种理论参考声速计算方法，而后推导了一种水平线列阵方位-相速度联合的纯方位扩展卡尔曼滤波(Cs bearing only extended Kalman filter,Cs-BO-EKF)方法，仿真结果表明，Cs-BO-EKF 方法在跟踪过程中实时估计相速度，提高了测向精度，相比纯方位扩展卡尔曼滤波(Bearing only extended Kalman filter,BOEKF)算法，降低了受测向误差的影响，具有更高的跟踪精度及稳健的跟踪性能，具有较好的应用前景。

1 参考声速对水平线列阵测向精度影响的理论分析

传统的水平均匀直线阵被动测向法，是基于信号以平面波传播的假设[15−16]：各阵元接收到同一目标的信号波形相同，仅是时延不同。如图1 所示，一个由M个阵元组成的均匀直线阵，阵元间距为d，平面波入射方向与基阵法线方向夹角为θ0，其中令沿着基阵正横方向入射的角度为0◦，沿着基阵左端入射的角度为−90◦，沿着基阵右端入射的角度为90◦。由于各阵元位置不同，使得信号源到达各个阵元具有不同的时延。

图1 波束形成示意图Fig.1 Schematic diagram of beamforming

设首阵元为参考阵元，接收到的信号为x1(t)，则第m号阵元接收到的信号为

其中，τm(θ0)为第m号阵元相对于参考阵元的时延，

其中，c为参考声速。声信号到达不同阵元的时延是确定值，假设对应于信号真实入射角θ0的参考声速为c0，在实际计算中如果选用参考声速为c1，根据式(2)计算得到的角度为θ1，则它们满足下述公式：

由式(4)可知由于选取的参考声速c1相对于c0产生了∆c的偏差，导致测向结果相对于真值产生了∆θ的偏差。当信号以不同的角度入射时，选取的参考声速在不同的偏差的情况下所产生的测向偏差如图2所示。

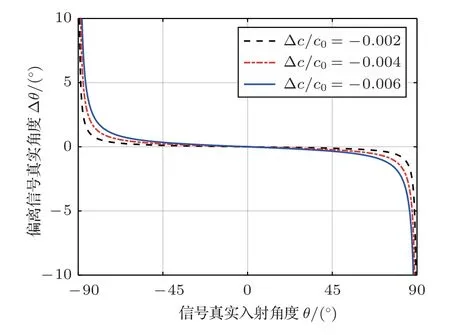
图2 不同入射角度下参考声速产生的测向误差Fig.2 Direction finding error caused by reference sound velocity at different incident angles

可以看到水平线列阵的测向误差与参考声速和信号的入射角度有关，当信号入射方向靠近基阵的正横方向时，参考声速的选取偏差不会导致明显的测向误差；当信号入射方向靠近基阵的端射方向时，参考声速的选取偏差会导致明显的测向误差，且参考声速偏差越大，测向误差越大。

2 理论参考声速的计算方法

根据简正波理论，浅海中声波是以多模态形式传播，参考声速与接收阵处的相速度密切相关，本节分别从简正波幅度加权和波束形成两个方面，给出在确知环境下的理论参考声速的计算方法。

2.1 简正波幅度加权法

根据简正波理论，声场中任一点处的声压是声源激发的多号简正波叠加的结果，即[17]

其中，pl为声源激发的第号简正波，令cpl为第l号简正波的相速度。将各号简正波的相对能量作为加权因子对相应号数的相速度进行加权并求和，作为该位置处的理论参考声速cs，即

2.2 波束形成计算法

已知目标距离rs与方位θs，选取声速搜索序列，如[c1,c2,···,cn]，由于声信号到达不同阵元间的时延值τ固定，即

遍历选取的声速值进行波束形成计算，得到波束形成角度估计序列[θ1,θ2,···,θN]，选取与目标角度相对误差最小的角度估计值对应的声速作为该目标距离下的参考声速。改变声源与接收阵的水平距离，得到不同距离下的理论参考声速。

3 Cs-BO-EKF方法

BOTMA 方法的基本原理是对运动目标，通过波束形成等方法得到方位观测序列，并利用该方位序列估计目标的位置和运动参数。为了分析方便，假设目标与观测站均在二维平面上，目标与观测站的运动态势图如图3所示。

图3 目标与观测站的运动态势示意图Fig.3 Movement situation diagram of target and observation station

将连续时间系统表示为离散形式，直角坐标系下，k时刻目标运动状态XT(k)和观测站运动状态XW(k)分别表示为

其中，rxt(k)和rxw(k)分别为k时刻目标和观测站沿X轴方向距离；ryt(k)和ryw(k)为k时刻目标和观测站沿Y轴方向的距离；vxt(k)和vxw(k)分别为k时刻目标和观测站沿X轴方向的速度；vyt(k)和vyw(k)分别为k时刻目标和观测站沿Y轴方向的速度。

则目标与观测站的相对运动状态为XR(k)=XT(k)−XW(k)：

其中，rx(k)和vx(k)分别为k时刻目标相对观测站沿X轴方向的距离和速度；ry(k)和vy(k)分别为k时刻目标相对观测站沿Y轴方向的距离和速度。

3.1 BO-EKF方法

对于匀速直线运动的目标，目标与观测站的相对运动状态方程为

T表示采样时间间隔，w(k)表示过程噪声，一般假设其满足零均值高斯分布，协方差矩阵为Q。目标方位的观测方程为

其中，εβ(k)表示测量噪声，满足零均值高斯分布，εβ(k)∼N(0,(k))。由于系统的观测方程非线性，因此对其进行泰勒级数展开取其一阶项来进行测量方程的线性化。一阶泰勒级数展开：

因此BO-EKF算法的迭代公式如下[2]：

其中，Xk+1|k为k+1时刻状态向量的预测值，Pk+1|k为k+1时刻状态向量的协方差矩阵的预测值，Gk+1为k+1时刻的卡尔曼增益，Xk+1|k+1为k+1 时刻状态向量的估计值，Pk+1|k+1为k+1时刻状态向量的协方差矩阵的估计值。

3.2 Cs-BO-EKF方法

对于匀速直线运动的目标，为校准参考声速，提高测向精度，将相速度cs(k)也作为估计状态量，目标与观测站的相对运动状态方程为

k时刻，选取参考声速为c0，β0(k)为按照此参考声速，利用波束形成获得的舷角估计值，βb(k)为对应相速度cs(k)的舷角真实值，则满足：

目标方位角与舷角的关系如图4 所示，其中β(k)为第k时刻目标方位真值，βb(k)为第k时刻目标相对于观测站的舷角真实值，βv(k)第k时刻观测站沿x轴方向的速度vxw(k) 与观测站速度的夹角。

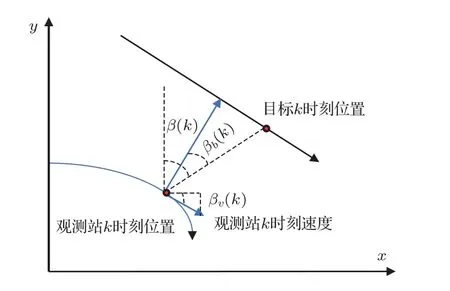
图4 角度示意图Fig.4 Angle diagram

由图4可知，目标方位角与舷角满足：

因此观测方程为

可以表示为

其中，εβ(k)表示测量噪声，满足零均值高斯分布，εβ(k)∼N(0,(k))。由于系统的观测方程非线性，因此对其进行泰勒级数展开取其一阶项来进行测量方程的线性化。一阶泰勒级数展开：

Cs-BO-EKF算法的迭代公式如下：

其中，Xk+1|k为k+1时刻状态向量的预测值，Pk+1|k为k+1时刻状态向量的协方差矩阵的预测值，Gk+1为k+1时刻的卡尔曼增益，Xk+1|k+1为k+1 时刻状态向量的估计值，Pk+1|k+1为k+1时刻状态向量的协方差矩阵的估计值。

4 仿真研究

4.1 理论参考声速的计算

以Pekeris 波导为例，海深100 m，水中声速1500 m/s，海水密度1.0 g/cm3，海底声速为1650 m/s，海底密度为1.6 g/cm3，海底衰减系数为0.3 dB/λ。接收阵由24 个间隔0.25 m 的阵元组成的水平均匀直线阵，深度为50 m。目标信号频率为450∼550 Hz，深度为25 m，角度为30◦。分别利用简正波幅度加权方法和波束形成方法计算不同距离处的理论参考声速如图5所示。

图5 理论参考声速Fig.5 Theoretical reference sound velocity

从仿真结果可以看出，两种方法计算得到的理论参考声速随距离变化的趋势一致，但使用波束形成方法计算的理论参考声速值在局部区域内存在抖动变化的情况，这是由于在不同距离处不同号数的简正波可能存在干涉现象；采用简正波幅度加权方法计算的理论参考声速值不存在局部抖动变化的情况，这是由于该方法不考虑简正波干涉情况，只是根据不同号数简正波的振幅对对应号数的相速度进行加权。

4.2 Cs-BO-EKF结果

相速度大小是由声源频率、声源距离、收发深度、海洋环境传播信道等因素决定，为探究该方法对于海洋环境的适应性，分别以不同海洋环境下阵列接收到的有效简正波号数多少进行讨论。

4.2.1 有效简正波号数相对较多情况

以Pekeris 波导为例，海深100 m，水中声速1500 m/s，海水密度1.0 g/cm3，海底声速为1650 m/s，海底密度为1.6 g/cm3，海底衰减系数为0.3 dB/λ。观测站为24 元水平均匀直线阵，阵元间距为0.25 m，深度为30 m。目标为单位强度的点源，信号频率为450∼550 Hz，深度为30 m，信噪比为0 dB。在当前海洋环境下，计算与观测站等深度，距离目标8200 m 处接收到的简正波号数共有60 号，其中高阶简正波(第24∼60 号简正波)在远距离传播时由于衰减过多导致其能量远小于低阶简正波能量，因此只选取前23 号简正波，计算各号简正波的相对能量，统计相对能量不低于0.1 倍的最大相对能量(图6 中红线)对应的简正波号数为该环境下的有效简正波，如图6所示，该海洋环境下对应的有效简正波号数共计13号。

图6 简正波能量分布Fig.6 Normal wave energy distribution

目标做匀速直线运动，目标速度为10 m/s，航向为170◦。观测站速度为4 m/s，初始航向为90◦，目标与观测站初始距离为12 km。观测站前300 s做匀速直线运动，然后以0.5◦/s 的角速度沿逆时针方向旋转150 s，之后做匀速直线运动。采样周期1 s，总观测时间50 min。目标与观测站的航迹如图7所示，目标相对于观测站的舷角变化如图8 所示。参考声速选取观测站所处深度处的海水声速即1500 m/s，进行常规波束形成方法得到的目标舷角误差如图9所示。由图8可以看到目标运动的第7∼20 min、第35∼50 min，目标位于观测站的近端射方向附近，因此参考声速的选取偏差会产生较大的测向误差。

图7 目标与观测站的航迹Fig.7 Movement situation of target and observation station

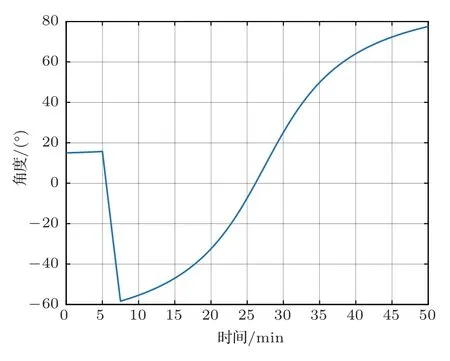
图8 目标舷角历程Fig.8 Angle change of target

图9 常规波束形成法得到的测向误差Fig.9 Error of direction finding obtained by conventional beamforming method

利用参考声速为1500 m/s 进行常规波束形成得到的测向结果，结合BO-EKF 算法和Cs-BOEKF 算法估计得到的目标跟踪结果如图10 所示，目标距离和速度的跟踪结果如图11和图12所示。

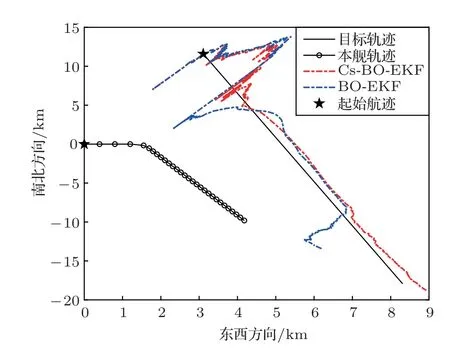
图10 两种滤波算法的跟踪结果Fig.10 Tracking results of two filtering algorithms

图11 目标距离跟踪结果Fig.11 Target range tracking results

由图10∼图12 可以看出，利用BO-EKF 算法得到的目标跟踪结果在35 min 之后开始发散，从图8、图9 中可以看到，由于在35 min 之后目标逐渐近观测站端射方向入射，采用参考声速1500 m/s 进行波束形成的测向结果误差逐渐变大，因此采用其结果直接作为观测值时，会因为角度估计误差过大导致BO-EKF 结果不收敛。由于Cs-BO-EKF 算法引入相速度作为状态估计量，可以迭代出整个跟踪过程中的相速度估计值，以此对测向结果进行校准，对比看出，Cs-BO-EKF 算法的跟踪性能更加稳健，且跟踪结果误差更低。

图13 是Cs-BO-EKF 算法对相速度估计的结果，图中Cp1 是利用简正波幅度加权方法计算得到的相速度，Cp2 是利用波束形成方法计算得到的相速度。

图13 相速度估计曲线Fig.13 Phase velocity estimation curve

可以看到，在前5 min 内，由于目标始终位于观测站基阵近正横方向，相速度估计值变化对角度估计值变化的影响较小，且此时滤波算法未收敛，因此会产生较大偏差。第5∼7.5 min 内，由于观测站转动，使得目标相对于观测站基阵的方向逐渐趋于端射方向，相速度估计值的变化对角度估计值影响较大，因此滤波算法中迭代的相速度值会逐渐收敛到相速度理论值。之后由于目标入射方向逐渐靠近基阵正横方向，此时参考声速的选取误差对测向结果的影响变小，故Cs-BO-EKF 在此区间内对相速度的估计值没有产生较大的变化，与理论值误差变大。随后在35 min 之后，由于目标入射方向逐渐靠近基阵端射方向，此时Cs-BO-EKF 算法对相速度的估计值与理论值又较为接近。

图14 是利用Cs-BO-EKF 算法估计的相速度值进行常规波束形成得到的测向结果误差，和参考声速为1500 m/s 进行常规波束形成得到的测向结果误差。当目标入射角度位于区间[−58◦,−45◦]利用相速度估计值得到的测向结果平均误差为0.530◦，利用参考声速1500 m/s 得到的测向结果平均误差为1.270◦；当目标入射角度位于区间[45◦,75◦]利用相速度估计值得到的测向结果平均误差为−0.768◦，利用参考声速1500 m/s 得到的测向结果平均误差为−2.173◦。可以看到利用Cs-BO-EKF算法提高了目标近端射方向入射时测向结果精度。

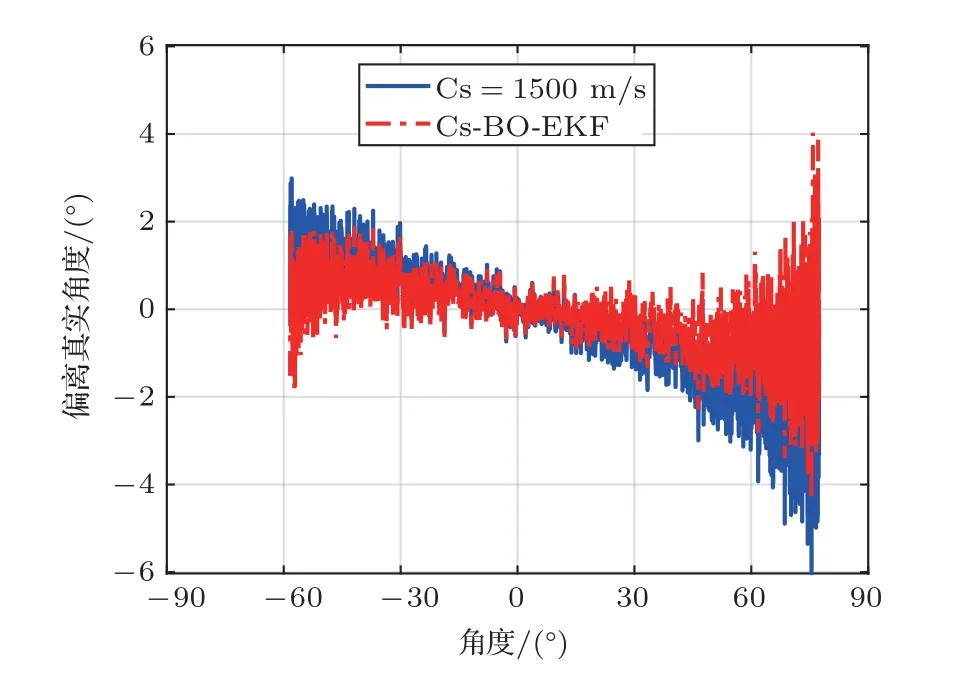
图14 测向结果误差曲线Fig.14 Error curve of direction finding

4.2.2 有效简正波号数相对较少情况

图15所示中等水文条件下的声速剖面，其中海面声速为1530 m/s，声速梯度为−0.05 m2/s，其余参数不变。在当前海洋环境下，计算与观测站等深度，距离目标8200 m 处接收到的简正波号数共有58 号，其中高阶简正波(第24∼58 号简正波)在远距离传播时由于衰减过多导致其能量远小于低阶简正波能量，因此只选取前23 号简正波，计算各号简正波的相对能量，如图16所示该海洋环境下对应的有效简正波号数共计6号。

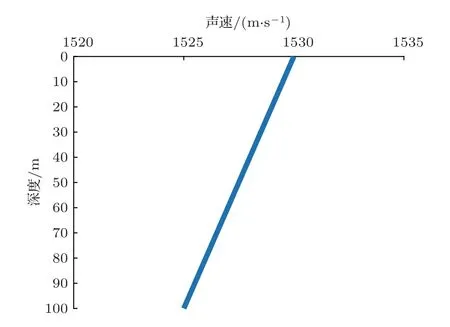
图15 声速剖面Fig.15 Sound speed profile

图16 简正波能量分布Fig.16 Normal wave energy distribution

参考声速选取观测站所处深度处的海水声速即1528 m/s，进行常规波束形成。BO-EKF 算法和Cs-BO-EKF 算法估计得到的目标跟踪结果如图17所示，目标距离和速度的跟踪结果如图18 和图19所示。

图17 两种滤波算法的跟踪结果Fig.17 Tracking results of two filtering algorithms

图18 目标距离跟踪结果Fig.18 Target range tracking results

图19 目标速度跟踪结果Fig.19 Target speed tracking results

可以看到，CS-BO-EKF 算法对目标的距离，速度的估计的精度都高于BO-EKF 算法，且Cs-BOEKF 算法的跟踪性能更加稳健。图20 是Cs-BOEKF算法对相速度估计的结果，可以看到相速度的估计值与理论计算的相速度值在目标入射方向位于观测站基阵近端射方向时较为吻合。图21是利用Cs-BO-EKF 算法估计的相速度进行常规波束形成得到的测向结果相对误差，和参考声速为1528 m/s进行常规波束形成得到的测向结果相对误差。当目标入射角度位于区间[−58◦,−45◦]利用相速度估计值得到的测向结果平均误差为0.579◦，利用参考声速1528 m/s 得到的测向结果平均误差为0.997◦；当目标入射角度位于区间[45◦,75◦]利用相速度估计值得到的测向结果平均误差为−0.235◦，利用参考声速1528 m/s 得到的测向结果平均误差为−1.547◦，可以看到利用Cs-BO-EKF 算法提高了目标近端射方向入射时测向结果精度。

图20 相速度估计曲线Fig.20 Phase velocity estimation curve

图21 测向结果误差曲线Fig.21 Error curve of direction finding

结合图13和图20，可以看到在不同的海洋环境下，由Cs-BO-EKF 方法估计的相速度与理论的相速度在目标近端射方向入射时均较为一致。

5 结论

针对水平线列阵因参考声速选取偏差造成的测向误差，从而导致BOTMA 方法在测向误差较大时跟踪结果不收敛的问题，本文提出了一种水平线列阵Cs-BO-EKF 方法，引入相速度作为估计状态量，实时校准参考声速，从而提高测向精度。浅海传播条件下的数值仿真结果表明，Cs-BO-EKF 方法相比BO-EKF 方法的跟踪性能更加稳健，跟踪精度更高。当目标接近水平线列阵端射方向时，本文所提方法的相速度估计值与理论计算的相速度值较为吻合，从而提高了目标近端射方向入射的测向精度。然而为满足BOTMA 系统的可观测性，该方法要求观测站至少进行一次有效的机动，在实际中不适用于隐蔽跟踪。