基于Rician分布散斑噪声的超声图像模拟算法∗

朋小秀 张 东

(武汉大学物理科学与技术学院 武汉 430072)

0 引言

超声成像技术由于其操作比较简单、对人体没有伤害等优点，成为了医学临床上广泛使用的诊断工具[1]，从而有大量的超声图像需要专家医生进行解读。而超声图像中存在大量颗粒状的斑点以及扁平的椭圆状纹理，即所谓的“散斑噪声”[2]。散斑噪声的存在影响了专家对病人病理的判断，降低了超声图像的可靠性[3]。因此，散斑噪声的相关问题是医学超声图像领域的一大研究重点，其一是对散斑统计的研究，最常用的模型之一是基于分辨率单元中包含大量散射体的假设，被称为完全发育的斑点噪声，根据中心极限定理，振幅被广泛认为满足瑞利分布[4−5]，但是当有孤立的强散射体存在时，将导致与瑞利统计的偏差，在这种情况下，后向散射振幅包络可以用Rician分布来表征[6−7]。

其二是对散斑噪声的抑制，由于真实的超声图像不存在无噪声的原图，为了评估各种去噪算法[8−11]的优劣，在理想的图像中添加可控噪声是非常有必要的。关于超声图像的模拟，Perreault等[12]提出一种基于超声图像的采集过程，并且加入由Goodman[13]提出、Burckhardt[14]推广到超声领域的散斑形成模型，是超声模拟算法中的一大进步，但是这个算法只能模拟完全发育的斑点噪声，即只能产生Rayleigh分布的斑点噪声。而在真实的超声图像中，分辨率单元中可能存在孤立的强散射体，本文基于这种情况，提出了一种基于Rician 的不完全发育斑点噪声的超声模拟算法，并以合成图像和肾脏图像为体模进行了模拟实验，通过在视觉上的对比以及对超声图像包络进行了直方图统计并进行了分布拟合检验，在理论和视觉上都证明了该算法的优越性。

1 方法

本文算法的主要步骤如图1 所示，主要部分一共分为4 个阶段，分别为采样过程、重构过程、加噪过程以及插值过程。

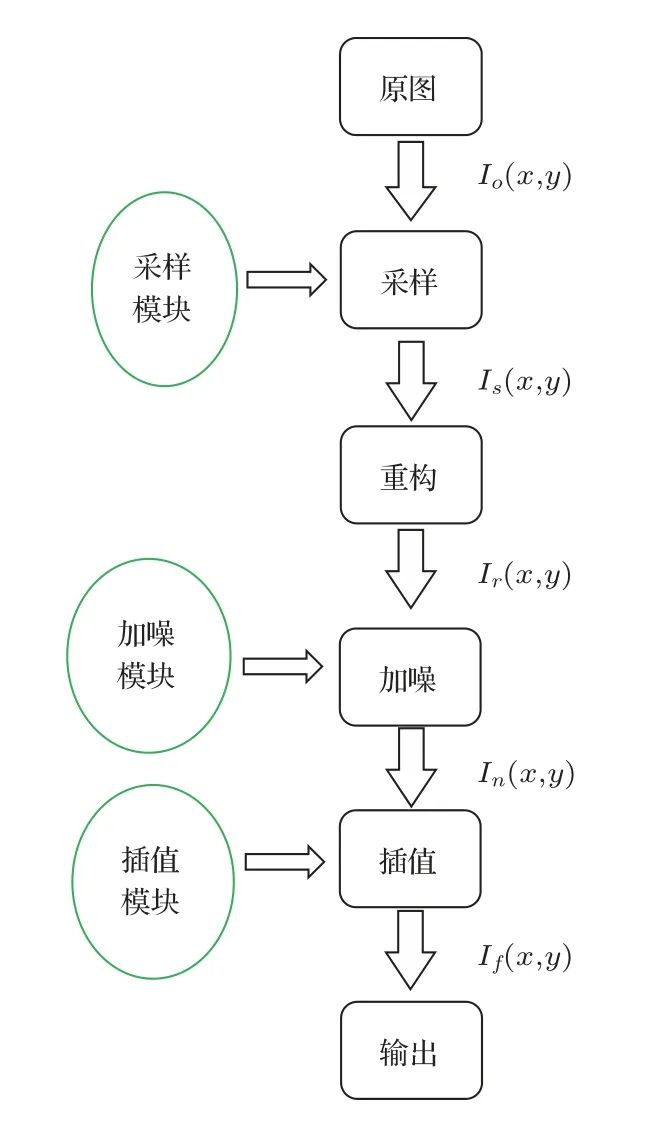
图1 算法流程Fig.1 Algorithm process

1.1 采样

本文算法的第一步是通过对像素网格进行采样来模拟超声波束对平面的扇形扫描。图2 为n条超声波束的扫描场景。图3 显示了采样网格所需要的参数，其中Φ表示扇形扫描的角度，w为原图像Io的宽度，h为原图像Io的高度，n为超声波束的条数，m为每条超声波束上采样的像素点数，h0是换能器距离图像上边界的距离，amin和amax分别为轴向扫描的最近和最远距离。这两个距离可以通过扫描超声波束与原图交点得到，但是一般可以根据实际超声图像的大小以及美观灵活地调节扇形区域的大小，从而可以得到更加贴近真实的模拟超声图像。用于计算采样点数据的伪代码如图4 所示，图4描述了对原始图像Io通过下采样的过程得到采样图Is。

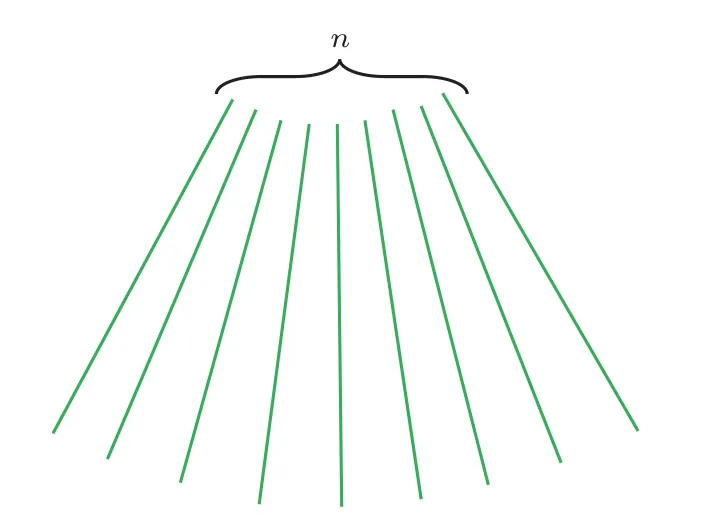
图2 n 条超声波束扫描场景Fig.2 n ultrasonic beam scanning scenario

图3 采样网格和算法参数Fig.3 Sampling grid and algorithm parameters

图4 通过径向极坐标采样计算采样点数据的伪代码Fig.4 Pseudo-code for calculating sampling point data by radial polar sampling

1.2 重构

本文算法的第二步是对采样图像进行校正。这里将由径向极坐标采样得到的点转换到的网格中，如图5 所示，其中P点映射到P′点，A区域映射到A′区域。用于计算校正图像的伪代码如图6 所示，将得到校正图像Ir(i,j)。从某种意义上，图6 的过程和图4的过程是等价的。

图5 采样点与校正图像中像素点的对应关系Fig.5 The correspondence between the sampling points and the pixels in the corrected image

图6 通过径向极坐标来进行采样的采样点来计算校正图像像素点的伪代码Fig.6 Pseudocode for calculating corrected image pixel points by sampling points in radial polar coordinates

1.3 加噪

本文算法的第三步是对采样图像进行加噪，也是核心部分。当超声脉冲的波长小于散射体大小时，会发生反射，发射的回波相位是相干的，经叠加后会产生反射分量也称镜面分量，而当超声脉冲的波长与散射体大小相当时，会产生散射分量。对于Rayleigh 噪声的模拟只考虑到散射分量，而当分辨率单元中存在孤立的强散射体时，就会存在一定的镜面分量[4,6]。

首先单色波方程为

式(1)中，B(x,y,z)表示幅度，t表示时间，w表示频率。其中幅度是一个复数值，即有

其中，|B(x,y,z)|为幅度的模，θ(x,y,z)为相位。单色波的幅度可以表示为

其中，f是一个任意变换(线性、非线性等)。假设无噪声图像Io以及采样并重构后的图像Ir的幅值(即灰度)为回波振幅的线性变换，按一个常数进行缩放，不失一般性，则有

根据物理学中的知识，复振幅可以通过回波分量ψi(x,y,z)来进行计算：

其中，M是相量ψi(x,y,z)的总数，而这些相量又可以分为两部分，镜面相量和散射相量，即：

其中，ψsi(x,y,z)是镜面相量，而ψdi(x,y,z)是散射相量，N为散射相量的数量，Bs是镜面相量叠加的结果，这里称为B的镜面分量，Bd是散射相量叠加的结果，这里称为B的散射分量。在本文的算法中，镜面分量来自于降采样之后的图像信息，而散射分量来自于散射体的回波在发生相互干扰之后产生的非相干回波。使用[0,2π]的均匀分布来表示非相干回波的相位独立性，不失一般性，假设每个相量ψdi(x,y,z)的实部和虚部都服从均值为0、方差为σ2的高斯分布，则散射分量的复分布由以下圆高斯分布的概率密度函数给出：

其中，u、v分别表示散射分量的实部和虚部，则散射分量的模V=(u2+v2)1/2将满足Rayleigh分布，概率密度函数如下：

当引入镜面分量之后，回波复振幅的模将满足Rician分布[15]，概率密度函数如下：

其中，A是主信号幅度的峰值δ2是多径信号分量的功率，I0()是修正的0阶第一类贝塞尔函数。并且有

其中，K称作莱斯因子，当A →0 时，莱斯分布转化为瑞利分布。

接下来散斑模拟算法主要分为以下几个步骤：

(1) 假设散射体的实部和虚部都服从高斯分布，为了方便计算，这里散射相量的数量N服从均匀分布U(c,d)，则：

其中，均匀分布的参数c和d可以随着像素点(x,y)的变化而变化。

(2) 计算降采样理想图像的每个像素(x,y)的幅值，每个像素对应的镜面分量累加到每个像素的散射特性上，来模拟每个像素点上复幅值的实部。累加散斑特性来模拟每个像素点上复幅值的虚部，则：

(3) 通过模拟出的每个像素点上复振幅的实部和虚部来进行最终的灰度幅值计算，来模拟不完全发育的斑点噪声：

用于上述计算的伪代码如图7所示。

图7 对每个采样像素点进行加散斑噪声的伪代码Fig.7 Pseudocode for adding speckle noise to each sampled pixel

1.4 插值

本文算法的最后一步是对重构图像进行插值操作，来获取完整的扇形图像。为了方便进行插值操作，这里使用卷积算子，因此进行了算法的第二步，对采样网格进行了矩形校正过程，创建了一个n×m的临时矩形图像Ir(i,j)。对于采样扇区内的每个像素，计算它的笛卡尔坐标，并插值周围的像素，插值会导致分辨率单元的形状发生改变，这与扫描的类型和扫描过程中所使用的插值技术有关，此处所采用的插值方法还是为双线性插值。

插值过程的伪代码如图8所示。

2 实验及结果分析

2.1 评价指标

为了保证模拟的超声图像更贴近真实的超声图像，需要对模拟的超声图像进行直方图统计并进行拟合，为了验证拟合得到的曲线是否符合超声图像的直方图分布，来定性分析模拟的图像是否从理论上符合真实的超声图像，需要对拟合结果进行一个评价，称之为拟合优度检验。在这一部分，采用3个指标来评估所提算法的性能。

(1) 判定系数(Coefficient of determination)[16]：判定系数在统计学中用于衡量因变量的变异中可以由自变量解释的部分所占的比例，用此来判断该统计模型的解释力。假设样本的数据集为y1,y2,···,yN，经拟合模型计算的得到的理论值为，可决系数的定义如下：

(2) KS(Kolmogorov Smirnov)检验[17−18]：KS检验是一种非参数检验，常用于判断数据样本与拟合模型给定的分布是否一致，假设N为样本数据集的数量，GN(x)为样本数据集的累计概率函数，G0(x)为待验证的累计分布函数，则KS检验的统计量定义为

在本文的计算中，KS统计量的简化计算公式为

当DobsDobs)计算得出：

(3) 卡方检验(Chi-Squared)[19]：卡方检验是统计样本数据的实际观测值和理论期望值之间的偏离程度。假设样本数据集中有N个数据，将其分到M个不相交的区间里面，每个区间对应的数据个数为Xi(i=1,2,···,M)，χ2检验的统计量为

其中，xi为理论分布对应区间的数据个数，需要注意的是xi需要大于5，小于5 的区间应该和前面的区间进行合并。卡方统计量的自由度为M−1−m，m为理论分布中需要估计的参数的个数，当M相对m来说比较大时，m可以忽略不计，则自由度近似为M−1。

然后将χ2检验统计量与根据显著性水平为α、自由度为M−1 时的χ2分布临界表进行比较。若，则拟合模型是可以被接受的，反之应该被拒绝。

卡方分布的累积分布函数为

其中，n为自由度，另外假设分布的可信度可以通过FM−1(χ2)得到

若显著性水平小于P值，不管χ2检验统计量大小如何，拟合模型都是可以被接受的。

2.2 实验材料

本文用的无噪声图像即体模是含有不同几何图形的合成图像，根据前人[8,20]的研究，这种设计是合理的。为了更加接近真实的超声图像，来自Field II Simulation Program 的肾脏图像也作为体模加入到实验中。肾脏图像可以在网站(http://field-ii.dk/)上找到。

2.3 实验结果

本文采用Microsoft Visual Studio 2019进行仿真实验，实验分为两组进行，第一组是人工合成的图像，第二组是肾脏图像，根据真实的超声成像过程，探头发射超声波的数量一般为128，即这里扇形的扫描条数n取128，散射分量的数量N服从[10,1000]的均匀分布，其中σ分别取0.5、1.0、1.5、2.0。另外这里还把生成的伪超声图像与真实的超声图像进行了对比。

2.3.1 实验一：合成图像

在作为体模的合成图像中，包括了三角形、圆形、矩形、菱形和箭头图案，大小为700×600，整个算法过程如图9所示，生成的图像如图10所示。

图9 本文算法以合成图像为体模的流程图(以δ=1.0 为例)Fig.9 The flow chart of using the synthetic image as the phantom in the algorithm in this paper (take δ=1.0 as an example)

图10 本文算法处理结果Fig.10 The results of the algorithm in this paper

2.3.2 实验二：肾脏图像

在这个部分的实验，使用肾脏图像作为模型，大小为522×469，整个算法过程如图11所示。生成的图像如图12所示。

图12 本文算法处理结果Fig.12 The results of the algorithm in this paper

2.3.3 与真实的超声图像的对比

为了从视觉上证明本文算法的合理性，将上述实验的结果与真实的超声图像的细节进行对比，如图13 所示，其中图13(a)、图13(b)中伪超声图像的参数为N服从[10，1000]的均匀分布，其中σ为1.0。本文实验用到的真实超声图像来自于重庆医科大学附属医院，是高强度聚焦超声导航的子宫肌瘤图像。

图13 本文算法结果与真实超声图像的对比图Fig.13 Comparison between the results of the algorithm in this paper and the real ultrasound images

从图10 和图12 以及图13 的实验结果可知，该算法模拟的不完全发育的斑点噪声在视觉上非常接近真实的超声图像，都有着弧状的椭圆形纹理噪声。并且本文算法还可以生成与原图对应的无噪声图像，如图10(b)、图12(b)所示，这为各种去噪算法的评价提供了便利条件。

2.4 分布拟合结果

2.3节已经从视觉上证明了本文算法的优越性，为了对实验结果进行更全面的评价，本节将从理论上定性地验证本文算法的正确性。

首先对图像噪声分布进行相似区域(即同质区)的矩形窗口采样，再对采样区域进行直方图统计，最后对此进行拟合评价。这里根据概率论知识里面的各态历经性，取一定数量的散射分量的模拟超声图进行分析(其实只要保证相同灰度的区域对应的散射分量数量一致即可，这里为了简便不做个别区分)。分别对不同的散射分量数量的模拟超声图的不同位置进行分析，不失一般性，这里取散射分量数量为100、δ为0.15 的情况来进行展开分析，这里选的采样的窗口的大小为50× 50 的正方形区域，具体采样区域如图14 所示，并通过遗传算法和列文伯格-马夸尔特(简称LM)算法相结合的方法对直方图进行Rician 分布的拟合，拟合结果如图15 所示。对于上述实验中的4 组样本的Rician 分布拟合，所拟合的参数分别为σ=32.0984、A=124.8432；σ=28.9569、A=120.9332；σ=37.2979、A=125.6149；σ=32.8162、A=115.3947，根据可决系数、KS检验、卡方检验对拟合的评价方法，对拟合结果的评价具体如表1 所示(其中表2[17,21]为检验评价常用的参数临界值)，由表1 的结果可知，KS 和卡方两种检验都认为所列的显著性水平下，Rician 分布的假设是成立的，而可决系数也是都大于0.98，接近于1，即一致验证了在散射分量数量为100 的情况下，模拟噪声图像在不同的区域下都是符合Rician分布的。

表1 散射相量数量为100、δ 为1.5 时，KS 检验和卡方检验在样本为2500、卡方自由度为47 时，不同显著性水平下被接受的情况以及可决系数的数值Table 1 When the number of scattering components is 100 and δ is 1.5,the KS test and the chi-square test are accepted at different significance levels and the values of the coefficient of determination when the sample is 2500 and the chi-square degree of freedom is 47

表2 KS 检验和卡方检验在样本为2500、卡方检验自由度为47 时，不同显著性水平下对应的临界值Table 2 Corresponding critical values of KS test and chi-square test at different significance levels when the sample is 2500 and the chi-square degree of freedom is 47

图14 从模拟的图像截取不同的区域用于Rician分布拟合Fig.14 Crop different regions from the simulated image for Rician distribution fitting

图15 散射相量数量为100、δ 为1.5 时的不同区域的Rician 分布拟合情况Fig.15 Fitting of Rician distribution in different regions when the number of scattering phasors is 100 and δ is 1.5

3 结论

本文提出了基于Rician 分布的不完全发育的散斑噪声超声图像模拟算法，考虑到了真实的分辨率单元中会存在孤立的强散射体的情况，并且结合了真实的超声成像过程。另外本文算法可以生成一张没有加噪的采样插值图像，为后续的去噪等应用的评价工作创造了条件。同时利用可决系数的值以及KS 和卡方两种检验方法对模拟噪声进行噪声分布拟合评价，证明本文算法模拟的伪超声图像从视觉和理论上都接近真实的超声图像。